Schneider P., Eberly D.H. Geometric Tools for Computer Graphics

Подождите немного. Документ загружается.

584 Chapter 11 Intersection in 3D

If a triangle intersects a cone, it must do so either at a vertex, an edge point, or an

interior triangle point. The algorithm described here is designed to provide early exits

using a testing order of vertex-in-cone, edge-intersects-cone, and triangle-intersects-

cone. This order is a good one for an application where a lot of triangles tend to be

fully inside the cone. Other orders may be used depending on how an application

structures its world data.

To test if P

is inside the cone, it is enough to test if the point is on the cone side

of the plane a ·(X − V)≥ 0 and if the point is inside the double cone. Although the

test can be structured as

D0 = triangle.P0 - cone.V;

AdD0 = Dot(cone.A, D0);

D0dD0 = Dot(D0, D0);

if (AdD0 >= 0 and AdD0 * AdD0 >= cone.CosSqr * D0dD0)

triangle.P0 is inside cone;

if all the triangle vertices are outside the single cone, it will be important in the edge-

cone intersection tests to know on which side of the plane a ·(X −V)=0 the vertices

are. The vertex test is better structured as shown below. The term outside cone refers

to the quantity being outside the single cone, not the double cone (a point could be

outside the original single cone, but inside its reﬂection).

D0 = triangle.P0 - cone.V;

AdD0 = Dot(cone.A, D0);

if (AdD0 >= 0) {

D0dD0 = Dot(D0, D0);

if (AdD0 * AdD0 >= cone.CosSqr * D0dD0) {

triangle.P0 is inside cone;

} else {

triangle.P0 is outside cone, but on cone side of plane;

}

} else {

triangle.P0 is outside cone, but on opposite side of plane;

}

All three vertices of the triangle are tested in this manner.

If all three vertices are outside the cone, the next step is to test if the edges

of the triangle intersect the cone. Consider the edge X(t) = P

+ t e

,wheree

− P

and t ∈ [0, 1]. The edge intersects the single cone if a ·(X(t) − V)≥ 0 and

(a · (X(t) − V))

−γ

X(t) − V 

=0 for some t ∈[0, 1]. The second condition is

a quadratic equation, Q(t) = c

+ 2c

t + c

= 0, where c

= (a ·e

)

− γ

e



=(a ·e

)(a ·



) − γ

e



, and c

=(a ·



)

−γ







,where



' = P

−V .

The domain of Q(t) for which a root is sought depends on which side of the plane

the vertices lie.

11.7 Planar Components and Quadric Surfaces 585

If both P

and P

are on the opposite side of the plane, then the edge cannot

intersect the single cone. If both P

and P

are on the cone side of the plane, then

the full edge must be considered, so we need to determine if Q(t) = 0 for some

t ∈ [0, 1]. Moreover, the test should be fast since we do not need to know where the

intersection occurs, just that there is one. Since the two vertices are outside the cone

and occur when t = 0 and t = 1, we already know that Q(0)<0 and Q(1)<0. In

order for the quadratic to have a root somewhere in [0, 1], it is necessary that the

graph be concave, since if it were convex, the graph would lie below the line segment

connecting the points (0, Q(0)) and (1, Q(1)). This line segment never intersects the

axis Q = 0. Thus, the concavity condition is c

< 0. Additionally, the t-value for the

local maximum must occur in [0, 1]. This value is

t =−c

. We could compute

directly by doing the division; however, the division can be avoided. The test 0 ≤

t ≤1

is equivalent to the test 0 ≤ c

≤−c

since c

< 0. The ﬁnal condition for there to

be a root is that Q(

t) ≥ 0. This happens when the discriminant for the quadratic is

nonnegative: c

− c

≥ 0. In summary, when P

and P

are both on the cone side

of the plane, the corresponding edge intersects the cone when

< 0 and 0 ≤c

≤−c

and c

≥ c

If P

is on the cone side and P

is on the opposite side, the domain of Q can be

reducedto[0,

t], w h er e P

t e

is the point of intersection between the edge and the

plane. The parameter value is

t =−(a ·



)/(a ·e

). If this point is V and it is the only

intersection of the edge with the cone, at ﬁrst glance the algorithm given here does not

appear to handle this case because it assumes that Q<0 at the end points of the edge

segment corresponding to [0,

t]. It appears that Q(

t) = 0 and c

≥ 0 are consistent

to allow an intersection. However, the geometry of the situation indicates the line

containing the edge never intersects the cone. This can only happen if Q(t) ≤ 0, so

it must be the case that c

< 0 occurs. Now we analyze when Q has roots on the

interval [0,

t]. As before, c

< 0 is a necessary condition since Q(0)<0 and Q(

t)< 0.

The t-value for the local maximum must be in the domain 0 ≤

t ≤

t. To avoid the

divisions, this is rewritten as 0 ≤ c

and c

(a ·



) ≤ c

(a ·e

). The condition that

the discriminant of the quadratic be nonnegative still holds. In summary, when P

on the cone side and P

is on the opposite side, the corresponding edge intersects the

cone when

< 0 and 0 ≤c

and c

(a ·



) ≤ c

(a ·e

) and c

≥ c

Finally, if P

is on the cone side and P

is on the opposite side, the domain for Q

isreducedto[

t, 1]. Once again the graph must be concave, the discriminant of the

quadratic must be nonnegative, and

t ∈ [

t, 1]. The edge intersects the cone when

< 0 and c

≤−c

and c

(a ·



) ≤ c

(a ·e

) and c

≥ c

All three edges of the triangle are tested in this manner.

586 Chapter 11 Intersection in 3D

If all three edges are outside the cone, it is still possible that the triangle and

cone intersect. If they do, the curve of intersection is an ellipse that is interior to the

triangle. Moreover, the axis of the cone must intersect the triangle at the center of that

ellipse. It is enough to show this intersection occurs by computing the intersection

of the cone axis with the plane of the triangle and showing that point is inside the

triangle. Of course this test does not need to be applied when all three vertices are on

the opposite side of the plane—another early exit since it is known by this time on

which side of the plane the vertices lie.

A triangle normal is n =e

×e

. The point of intersection between cone axis

V +s a and plane n · (X −P

) = 0, if it exists, occurs when s =(n ·



)/(n ·a).The

point of intersection can be written in planar coordinates as

V + s a =P

+ t

e

+ t

e

(n ·



)a −(n ·a)



= t

(n ·a)e

+ t

(n ·a)e

Deﬁne u = (n ·



)a −(n ·a)



.Tosolvefort

, cross the equation on the right

with e

, then dot with n. Similarly solve for t

by crossing on the right with e

and

dotting with n. The result is

(n ·a)n

=n ·u ×e

and t

(n ·a)n

=−n ·u ×e

To be inside the triangle it is necessary that t

≥0, t

≥0, and t

≤1. The compar-

isons can be performed without the divisions, but require two cases depending on the

sign of n ·a. In the code, the quantities n, n ·a, n ·



, u, and n ×u are computed.

If n ·a ≥0, then the point is inside the triangle when n ×u ·e

≤ 0, n ×u ·e

≥ 0,

and n ×u ·e

≤ (n ·a)n

. The inequalities in these three tests are reversed in the

case n ·a ≤0.

Find Intersection

The analysis in the previous section can be extended to actually partition the triangle

into the component inside the cone and the component outside. The curve of sepa-

ration will be a quadratic curve, possibly a line segment. If the triangle is represented

as X(s, t) = P

+ s e

+ t e

for s ≥0, t ≥ 0, and s + t ≤ 1, the points of intersetion

of the single cone and triangle are determined by

a ·(X(s, t) − V)≥ 0 and (a · (X(s, t) − V))

− γ

X(s, t)

= 0

If any portion of the triangle satisﬁes the linear inequality, this trims down the tri-

angle domain to a subset: the entire triangle, a subtriangle, or a subquadrilateral. On

11.8 Planar Components and Polynomial Surfaces 587

that subdomain the problem is to determine where the quadratic function is zero.

Thus, the problem reduces to ﬁnding the intersection in 2D of a triangle or quadri-

lateral with a quadratic object. Locating the zeros amounts to actually ﬁnding the

roots of Q(t ) for the edges of the triangle discussed in the previous section, and/or

determining the ellipse of intersection if the cone passes through the triangle interior.

11.8

Planar Components and Polynomial

Surfaces

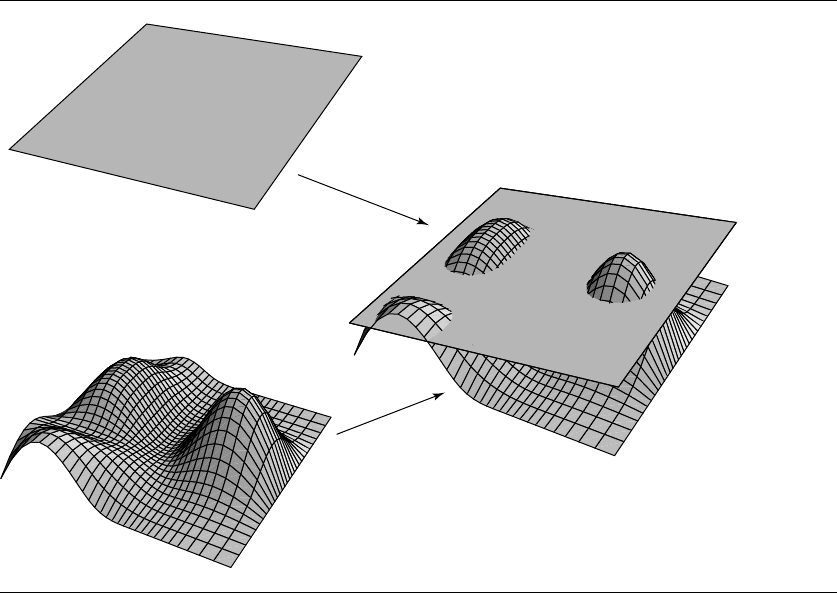
In this section we cover the problem of intersecting a plane with a polynomial surface,

an example of which can be seen in Figure 11.53.

A very general way to represent a polynomial surface is in rational parametric

form

Figure 11.53 Intersection of a plane and a parametric surface.

588 Chapter 11 Intersection in 3D

x =

x(s, t)

w(s, t)

y =

y(s, t)

w(s, t)

z =

z(s, t)

w(s, t)

(11.27)

where the polynomials x(s, t), y(s, t), and z(s, t) may be in monomial, B

ezier, B-

spline, or other piecewise polynomial basis. Given this, two general methods may be

employed to ﬁnd the intersection of such a polynomial surface with a plane.

One method is to apply a series of transformations (rotation and translation) to

map the intersecting plane into the XY plane. The same transformation applied to

the polynomial surface results in



(s, t)



(s, t)



(s, t)



(s, t)



(s, t)



(s, t)

The equation z



= 0 now represents the intersection in the parameter space of the

rational polynomial surface.

The other method works the other way around—substitute the parametric equa-

tions of the polynomial surface into the plane equation

ax + by + cz + d = 0

If we substitute the expressions in Equation 11.27 into this plane equation, we get

ax(s, t) + by(s, t) + cz(s, t) + dw(s, t) = 0

the equation of the intersection curve in the parameter space of the surface.

We could also simply treat the plane–polynomial surface intersection problem as

just an instance of the general surface-surface intersection problem (Section 11.10).

Owing to the low degree of the plane, and the fact that the plane is of course ﬂat, such

an approach would probably be relatively reliable. However, we can more directly take

advantage of the fact that one of the surfaces is a plane and derive a more efﬁcient

and robust algorithm for this special case. Two such algorithms are found in Boeing

(1997) and Lee and Fredricks (1984). We present the latter here.

11.8 Planar Components and Polynomial Surfaces 589

11.8.1 Hermite Curves

The intersection method we’ll describe produces an (approximate) intersection curve

using the Hermite form, and so we provide a brief review of this representation.

A Hermite curve is deﬁned by its two end points P

and P

and two tangent

vectors



and



. The cubic Hermite basis functions are

(t) = 2t

− 3t

+ 1

(t) =−2t

+ 3t

(t) = t

− 2t

+ t

(t) = t

− t

The basis functions are shown in Figure 11.54.

The curve is a linear combination of the points and tangents, using the (cubic)

Hermite basis functions a

(t), a

(t), b

(t), and b

(t) :

C(t) = a

(t)P

+ a

(t)P

+ b

(t)



+ b

(t)



0.2 0.4 0.6 0.8 1

0.2

0.4

0.6

0.8

Figure 11.54 Hermite basis functions (cubic).

590 Chapter 11 Intersection in 3D

Figure 11.55 Cubic Hermite curve, speciﬁed by end points and tangents.

An example of such a curve is shown in Figure 11.55. (Note that the tangents are not

drawn to scale for space reasons;



should be

√

10 times as long as drawn, and



should be 5 times as long as drawn.)

11.8.2 Geometry Deﬁnitions

We’re interested in the intersection of a plane P and a parametric surface S deﬁned

as S(u, v). For convenience of discussion, we assume that the parameter domains are

0 ≤ u, v ≤ 1. A surface may be viewed as the union of a number of subpatches, and

this algorithm concentrates on the intersection of a subpatch with P; the complete

intersection is found by ﬁnding the intersection curves for each subpatch and con-

catenating these curves into one or more intersection curves for the entire surface. A

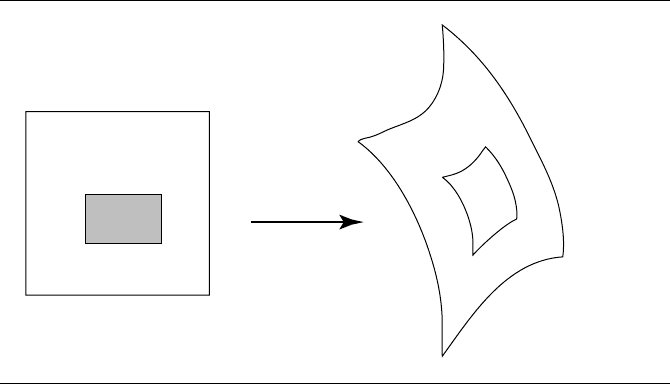
subpatch is denoted by its corners in parameter space (a, b, c, d),where(a, b) are the

coordinates of the lower-left corner and (c, d) are the coordinates of the upper-right

corner, as shown in Figure 11.56.

Let the intersection of the surface S and the plane P be R(t), and let its preimage

be p(t) = [

u(t) v(t )

]. We wish to ﬁnd a curve that approximately solves R(t) =

S(p(t)). The algorithm consists of a two-stage recursive method that computes cubic

Hermite approximations to (segments of) R(t) and p(t). Note that the Hermite curve

segments, whose union comprises the intersection curves proper, is a curve deﬁned

in 3-space. The approximation criteria are as follows:

For p(t), an approximation is considered “sufﬁcient” if its corresponding image

in 3-space is in the plane P.

For R(t), an approximation is considered “sufﬁcient” if it is within a speciﬁed

tolerance of the 3-space image of the corresponding parameter space segment.

11.8 Planar Components and Polynomial Surfaces 591

(1, 1)

(a, b)

(c, d )

S(a, b)

S(c, d )

(0, 0)

Figure 11.56 A subpatch in parameter space maps to a topologically rectangular region on the

patch. After Lee and Fredricks (1984).

11.8.3 Computing the Curves

Recalling that we’re using a cubic Hermite curve, the tangent vector of R(t) is



(t) = S

(p(t))u



(t) + S

(p(t))v



(t) (11.28)

where S

(p(t)) and S

(p(t)) are the partial derivatives with respect to u and v at pa-

rameter t, and u



and v



are the components of the tangent vector of p at parameter t.

Because all points in R(t) must lie in P, it must be the case that



(t) ·ˆn =0

where ˆn is the unit normal to P. Substituting Equation 11.28, we have



(p(t)) ·ˆn





(p(t)) ·ˆn



Atapointp(t), this equation gives us the tangents for R(t). The (initial) estimates

of the lengths are computed by estimating one of u



(t) or v



(t), and solving for the

other one. The estimates are reﬁned by making sure that the image of the midpoint

of p(t) is contained in P.

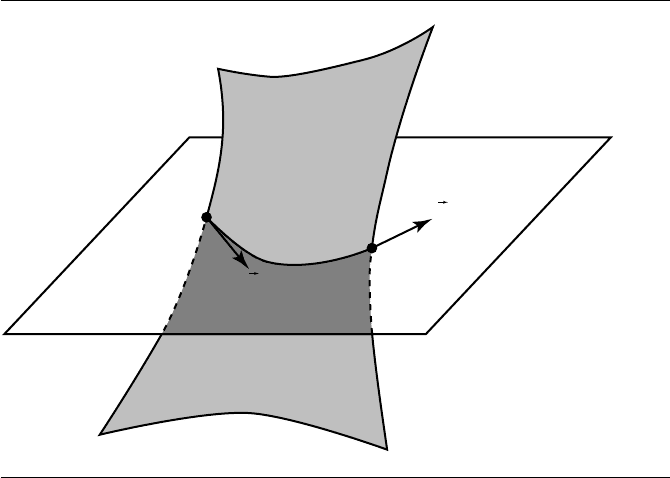
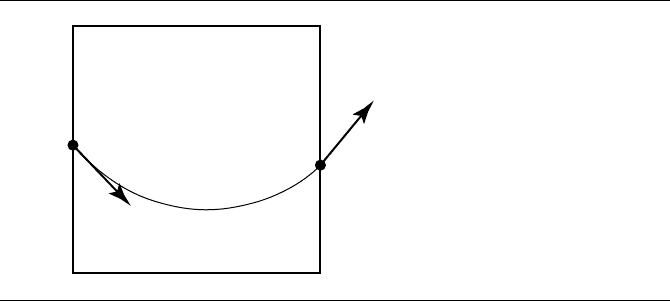
Figures 11.57 and 11.58 show the curves R(t) ={P

, P



} and p(t) =

{(u

, v

), (u

, v

), (u



, v



), u



, v



}, respectively (again, the tangent vectors are not

drawn to scale).

592 Chapter 11 Intersection in 3D

Figure 11.57 3-space intersection curve R(t).

11.8.4 The Algorithm

The algorithm consists of three parts, the ﬁrst two recursive. The ﬁrst part subdivides

the surface S into subpatches, until either no intersections are found, or until a

subpatch is found that intersects P exactly twice along its (the patch’s) borders. Each

subpatch so found is then passed, along with the 3D intersection points along each of

the two intersecting borders, to the second recursive algorithm, which computes the

intersection curve (segment).

The pseudocode is as follows:

Find(S, P, a, b, c, d) {

// Compute intersections along borders, if any

hits = ComputeIntersectionWithPlane(u0, v0, u1, v1, border0, border1);

if (hits == 0) {

return;

}

// Check for two hits, on different borders

if (hits == 2 and border0 != border1) {

11.8 Planar Components and Polynomial Surfaces 593

, v

)

, v

)

(u'

, v'

)

(u'

, v'

)

Figure 11.58 Parametric space intersection curve p(t).

// Get the 3D points of the intersections

p0 = S(u0, v0);

p1 = S(u1, v1);

ComputeCurve(S, P, u0, v0, u1, v1, p0, p1);

} else {

// Split the subpatch in half, alternating

SplitSubPatch(S, a, b, c, d, parm, whichDirection);

// Recursively solve each half

if (whichDirection == uDir) {

Find(S, P, a, b, parm, d);

Find(S, P, parm, b, c, d);

} else {

Find(S, P, a, b, c, parm);

Find(S, P, a, parm, c, d);

}

The second part computes the intersection curve, recursively improving the ap-

proximation. As Lee and Fredricks (1984) note, the recursion is binary—that is, the

curve is checked at its midpoint, and if it fails to meet the convergence criteria, it is

split there and the algorithm recurses—but they suggest that it may be better to split

the curve into more than two pieces.