Schneider P., Eberly D.H. Geometric Tools for Computer Graphics

Подождите немного. Документ загружается.

564 Chapter 11 Intersection in 3D

Figure 11.42 Intersection of a plane and a cone.

Intersection Detection

For the intersection detection algorithm, we’ll deﬁne a plane implicitly:

P ·ˆn + d = 0

(The coordinatized version is the usual ax + by + cz + d = 0, where

√

+ b

+ c

= 1.) The ﬁnite single cone is deﬁned in “general position”—as a

base point B, axis

d, and height h (see Figure 11.14 in Section 11.3.5). An inﬁnite

single cone is deﬁned by a point A deﬁning the apex of the cone, an axis

d, and a

half-angle α (see Figure 11.44).

Inﬁnite Cone

For the purposes of detecting an intersection, a plane P and an inﬁnite cone C can

be in one of several conﬁgurations:

1. If P is parallel to C’s axis,

d ·ˆn =0, then there will always be an intersection.

2. If P is perpendicular to C’s axis, |

d ·ˆn|=1, there will be an intersection if the

(signed) distance from the cone’s apex A to the plane is nonpositive (with respect

d).

3. If P is neither perpendicular nor parallel to C’s axis, then there may or may not

be an intersection, depending on the distance from A to the intersection of the

11.7 Planar Components and Quadric Surfaces 565

Point Circle Ellipse Single line (segment)

Point (finite cone only) Two lines (segments) Hyperbola ( arc) Parabola (arc)

Figure 11.43 Some of the ways a plane and a cone can intersect.

cone’s axis and the plane, and the relative angle between the cone’s axis and the

plane.

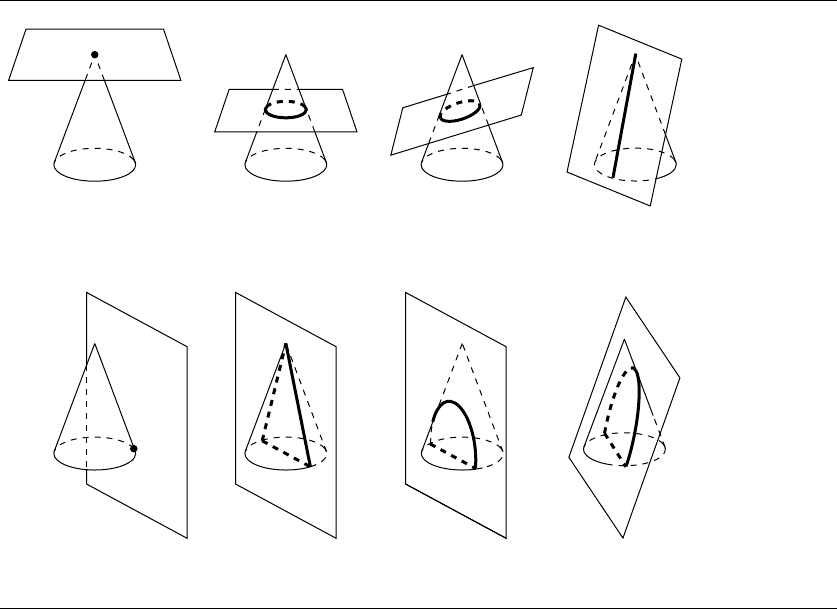
Figure 11.44 shows the intersection test for a cone with a plane, for the case where

the cone’s axis and the plane are neither perpendicular nor parallel. The plane P

⊥

perpendicular to P and going through A is parallel to

d, and so its normal is

ˆn ×

WedeﬁneavectorinP

⊥

that is perpendicular to

ˆw =

d × ( ˆn ×

566 Chapter 11 Intersection in 3D

nˆ

Figure 11.44 Intersection test for a plane and an inﬁnite cone.

The angle θ between ˆn and ˆw is

cos(θ) =ˆn ·w

If the intersection of the plane P and the axis of the cone is within the cone (i.e., the

signed distance less than or equal to zero), then there is obviously an intersection.

Otherwise, if θ ≤ α, then there is an intersection.

Finite Cone

For the purposes of detecting an intersection, a plane P andaconeC can be in one

of several conﬁgurations:

1. P may be parallel to C’s axis: |

d ·ˆn|=1.

2. P may be perpendicular to C’s axis:

d ·ˆn =0.

3. P may be neither parallel nor perpendicular to C’s axis. In this case, P may or

may not intersect C.

11.7 Planar Components and Quadric Surfaces 567

Let’s consider these cases one by one:

1. If P is parallel to C’s axis, then there will be an intersection if the distance between

P and C’s axis is less than or equal to the radius of the cone.

2. If P is perpendicular to C’s axis, then there will be an intersection if the signed

distance (relative to

d)fromB to P is between 0 and h.

3. If P is neither parallel nor perpendicular to C’s axis, then there are two cases to

consider:

a. The signed distance (relative to

d)fromB to P is between 0 and h; in this

case, there is deﬁnitely an intersection.

b. P intersects the axis of C outside the apex or end cap of the cone, in which

case there may or may not be an intersection, depending on the relative

location of the point of intersection and the angle between the plane and the

axis.

All of the cases but the last are fairly trivial. Determining whether or not the plane

is parallel or perpendicular to the cone’s axis involves only a dot product. Computing

the distance between the cone’s base point B and the plane is simple and inexpensive

(see Section 10.3.1). Computing the intersection of the plane and the cone’s axis is

inexpensive as well (see Section 11.1.1). Only the last case has any expense associated

with it, and so the tests should be done in the order discussed.

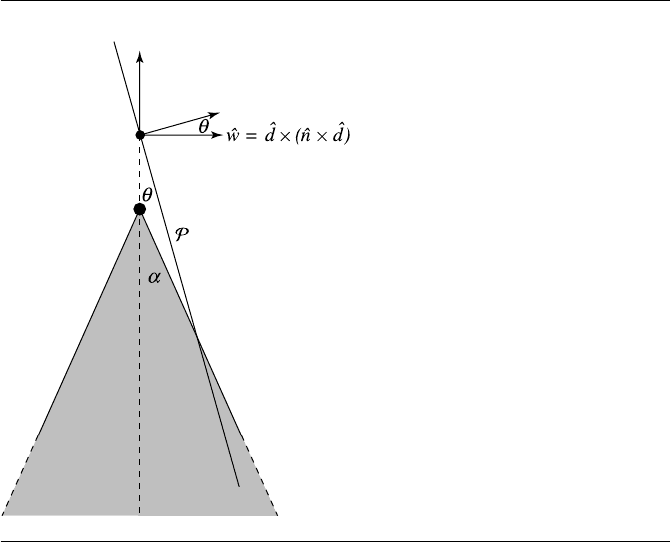
The last case is illustrated in Figure 11.45. The edge-on view is not simply a dia-

grammatic convenience—the method for determining whether or not an intersection

exists is done in a plane perpendicular to P and going through B. The rest is basic

trigonometry.

If I

is the intersection of P and the axis of the cone, then if the point I

is closer

to the axis than r (the radius of the cone), we have an intersection. The plane P

⊥

perpendicular to P and going through B is parallel to

d, and so its normal is

ˆn ×

WedeﬁneavectorinP

⊥

that is perpendicular to

ˆw =

d × ( ˆn ×

The angle θ between ˆn and ˆw is

cos(θ) =ˆn ·w

We also know the distance a:

a =I

− B−h

568 Chapter 11 Intersection in 3D

nˆ

Figure 11.45 Edge-on view of plane-cone intersection.

By the deﬁnition of the cosine function, we know

cos(θ) =

Substituting, we get

ˆn ·w =

I

− B−h

and so

c =

I

− B−h

ˆn ·w

11.7 Planar Components and Quadric Surfaces 569

Figure 11.46 Inﬁnite cone deﬁnition.

Invoking the Pythagorean Theorem, we have

+ b

= c

(I

− B−h)

+ b



I

− B−h

ˆn ·w





I

− B−h

ˆn ·w



− (I

− B−h)

and so if b

≤ r

, we have an intersection; otherwise, not.

Intersection with an Inﬁnite Cone

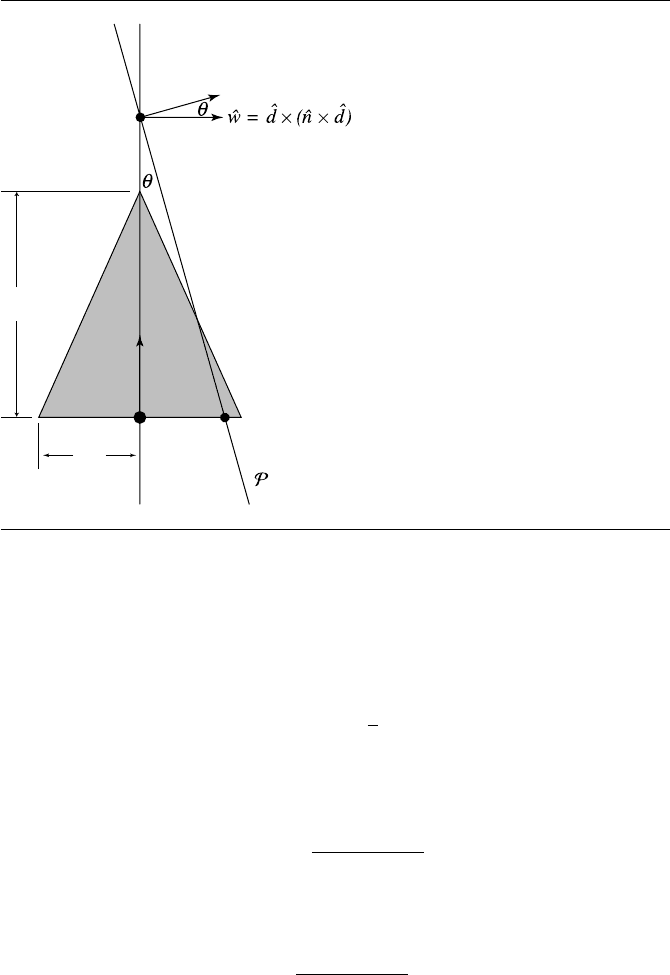
In this section, we address the problem of ﬁnding the intersection of a plane and an

inﬁnite cone. Here, we deﬁne a plane with a point P on the plane and a plane normal

ˆn; a cone is deﬁned by its vertex V , axis ˆa, and half-angle α, as shown in Figure 11.46.

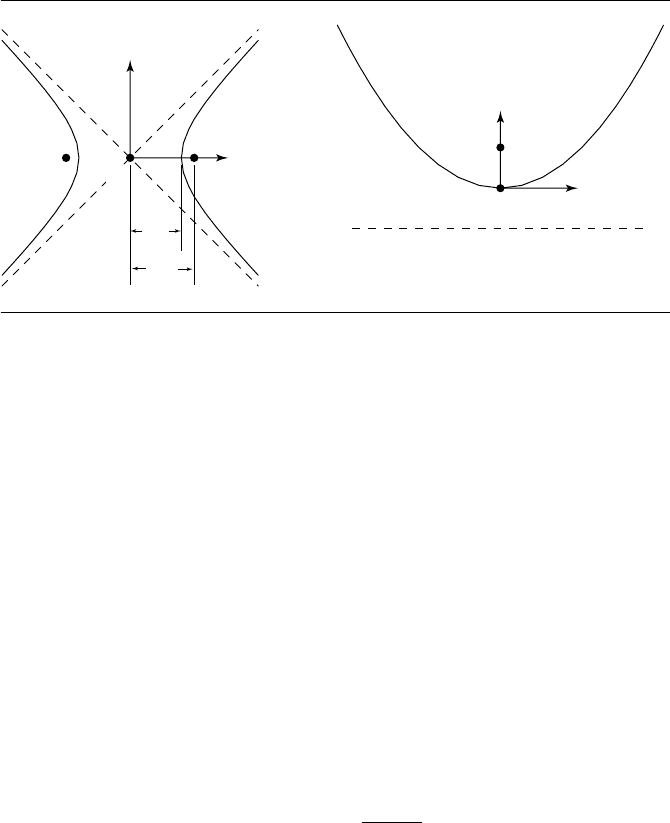
570 Chapter 11 Intersection in 3D

vˆ

Figure 11.47 Geometric deﬁnitions for hyperbola and parabola.

As with the problem of intersecting a plane with an inﬁnite cylinder (Sec-

tion 11.7.3), we present an approach due to Miller and Goldman (1992). In that

solution, they exploited Dandelin’s construction—a nondegenerate intersection re-

sults in a curve with a special relationship to spheres internally tangent to the cylinder

and tangent to the intersecting plane. For the problem of intersecting a plane and an

inﬁnite cone, a similar technique is applied. As pointed out previously (Figure 11.43),

a plane and a cone can intersect in a point, one line, two lines, circle, ellipse, parab-

ola, or hyperbola. The ﬁrst three cases we call “degenerate,” and the intersections are

fairly trivial to compute. The last four cases are conic sections, and to these we can

apply an analog to what was done with the plane-cylinder intersection.

The deﬁnitions of the ellipse and the circle were shown in Figures 11.37 and 11.38,

respectively, in the discussion of the intersection of a plane and a cylinder. For the

parabola and hyperbola, we have analogous geometric deﬁnitions: a parabola is de-

ﬁned by its vertex V

, directrix and focus vectors ˆu and ˆv, and focal length f (the

distance between V

and focus F ); a hyperbola is deﬁned by a centerpoint C, major

and minor axes ˆu and ˆv, and associated major and minor radii

and r



− r

where d is the distance between C and the foci F

and F

, as shown in Figure 11.47.

In the cases of nondegenerate intersection, either one or two spheres may be

found that are both tangent to the cone in a circle (that is, they ﬁt inside the cone)

and tangent to the intersecting plane. If the plane and cone intersect in a parabolic

curve, then there is one such sphere, and it touches the plane at the parabola’s focus.

If the plane and cone intersect in either an ellipse or hyperbola, then there are two

such spheres, and they touch the plane at the intersecting curve’s foci. As with the

plane-cylinder intersection, the distance along the surface of the cone, between the

11.7 Planar Components and Quadric Surfaces 571

two circles of tangency between the cone and spheres, is double the major radius of

the intersecting curve. A sketch of a proof of this is found in Miller and Goldman

(1992).

Conﬁgurations that result in degenerate intersections (point, one line, two lines)

are trivially identiﬁable by a shared characteristic—they all result when the apex of

the cone intersects the plane. Consider Figure 11.43: we can easily see this charac-

teristic in the “Point,” “Single line (segment),” and “Two lines (segments)” cases. It

should be noted that, in an implementation, the test for the cone’s apex being on

the plane should not be exact—some  should be applied; otherwise, the result in-

stead will be a conic section with at least one parameter (e.g., major radius) being

inﬁnitesimally small, which is undesirable computationally.

Nondegenerate Plane-Cone Intersections

In order to distinguish between the intersections, we consider the angle between the

cone’s axis ˆa and the plane’s normal ˆn, and its relationship to the half-angle α deﬁning

the cone. We deﬁne the angle between the cone’s axis and the plane’s normal as θ.By

the deﬁnition of the dot product, we then have cos(θ) =ˆa.

In order to exploit the tangent sphere properties, we ﬁrst need to determine where

the tangent spheres will be located, given the relative orientations of the cone and the

plane. We do this by determining the conditions for the sphere(s) to be tangent to the

cone, and the conditions for the sphere(s) to be tangent to the plane, and substituting

one equation into the other to determine what conditions must hold for the sphere

to be tangent to both. To simplify the situation, assume the following:

(V − P)·ˆn<0

ˆa ·ˆn ≥ 0

If either of these assumptions is not already met, simply reverse ˆn and/or ˆa.

Observing Figure 11.48, clearly the sphere {C, r}is located along the line V + t ˆa;

using the deﬁnition of the sine function, we have h =

sin(α)

, and so we then have

C =V +

sin(α)

ˆa (11.23)

Miller and Goldman note that r, if allowed to be negative, will generate the sphere on

the other side of the cone.

For the sphere to be tangent to the plane, by deﬁnition we must have the sphere’s

center C at a distance r from the plane; that is,

(C −P)·ˆn=|r|

or, squaring both sides,

((C −P)·ˆn)

= r

(11.24)

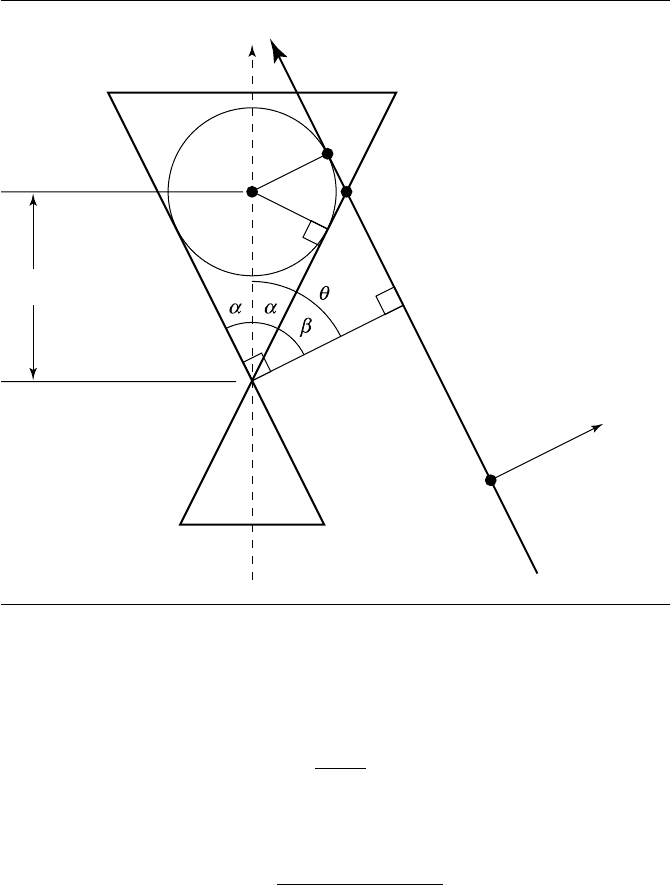
572 Chapter 11 Intersection in 3D

âˆv

ˆn

Figure 11.48 Parabolic curve intersection of plane and cone. After Miller and Goldman (1992).

If we substitute Equation 11.23 into Equation 11.24, we get



(V − P)+

sin(α)

ˆa



·ˆn



= r

This is a quadratic equation in r, whose solutions are

r =±

((V − P)·ˆn) sin(α)

sin(α) ∓ cos(θ)

(11.25)

The intersection is a parabola if the plane is parallel to a rule of the cone; that is,

when θ + α =π/2, as shown in Figure 11.48. Note that only one of the solutions for

r in Equation 11.25 is possible because when θ + α = π/2, we have cos(θ) = sin(α),

and one of the denominators of Equation 11.25 becomes 0. If we have cos(θ) =

sin(α), then Equation 11.25 becomes

11.7 Planar Components and Quadric Surfaces 573

r =−

(V − P)·ˆn sin(α)

sin(α) + cos(θ)

=−

(V − P)·ˆn sin(α)

2 sin(α)

=−

(V − P)·ˆn

The distance from the vertex of the cone to the plane is

d =−(V − P)·ˆn

and so we have

r =

(11.26)

To deﬁne the parabola, we need to ﬁnd the focal length f ,vertexV

, and the bases

ˆu and ˆv.Wecomputef by determining F (the focus of the parabola) and ﬁnding its

distance from the vertex V

f =F − V



Points V

and F lie in the plane containing V , ˆa, and ˆn, and F − V

ˆv; therefore,

ˆv lies in this plane as well. As it also must be perpendicular to the plane normal ˆn,we

have

ˆv =

ˆa −( ˆa ·ˆn) ˆn

ˆa − ( ˆa ·ˆn) ˆn

ˆa −cos(θ) ˆn

ˆa − cos(θ) ˆn

which gives us the direction between V

and F . To determine the positions of these

points, we need to compute the value e. We start by noting that β = θ − α = π/2 −

2α and tan(β) = e/a. Taken together, we have