Schneider P., Eberly D.H. Geometric Tools for Computer Graphics

Подождите немного. Документ загружается.

604 Chapter 11 Intersection in 3D

The object-type-speciﬁc implicit equations for the sphere, cone, and cylinder are

as follows:

Sphere: (P − B) · (P −B) − r

= 0 (11.35)

Cylinder: (P −B) · (P −B) − ((P − B) ·ˆw)

− r

= 0 (11.36)

Cone: ((P − B) ·ˆw)

− cos

(α)(P −B) · (P −B) =0 (11.37)

The basic steps of Miller’s method can be outlined as follows:

1. Choose one of the two (possibly) intersecting surfaces as the parameterization

surface.

2. Substitute the parametric form of the parameterization surface (e.g., Equa-

tion 11.33 or 11.34) into the implicit equation for the other surface (i.e., one

of Equations 11.35, 11.36, or 11.37).

3. Manipulate the resulting equation until it is in the form a(t)s

+b(t)s +c(t) =0.

The resulting equation’s functions a, b, and c will have, as Miller points out, “obvious

geometric interpretations.”

11.9.2 Ellipsoids

This section describes how to compute information about intersections of ellipsoids.

We cover the typical query: test for intersection without actually computing the

intersection set. Additionally we show how to determine if one ellipsoid is properly

contained in another. The latter method is based on the same idea shown in Section

7.5.3 for ellipses. The precise queries we answer for testing for intersection of two

ellipsoids E

and E

are

Do E

and E

intersect?

Are E

and E

separated? That is, does there exist a plane for which the ellipsoids

are on opposite sides?

Is E

properly contained in E

,orisE

properly contained in E

Finding the set of intersection points is more complicated. A couple of meth-

ods are discussed. In this section, ellipsoid E

is deﬁned by the quadratic equation

(X) = X

X +B

X +c

= 0, where A

isa3× 3 positive deﬁnite matrix, B

isa3× 1vector,c

is a scalar, and X

isa3× 1 vector that represents an ellipsoid

point. Because A is positive deﬁnite, Q

(X) < 0 deﬁnes the inside of the ellipsoid

and Q

(X) > 0 deﬁnes the outside.

11.9 Quadric Surfaces 605

Testing for Intersections

The analysis is based on level surfaces of the quadratic functions. Section A.9.1 pro-

vides a discussion of level sets of functions. All level surfaces deﬁned by Q

(x, y, z) =

λ are ellipsoids, except for the minimum (negative) value λ for which the equation

deﬁnes a single point, the center of every level surface ellipsoid. The ellipsoid deﬁned

by Q

(x, y, z) = 0 is a surface that generally intersects many level surfaces of Q

.The

problem is to ﬁnd the minimum Q

-level value λ

and the maximum Q

-level value

attained by any point (x, y, z) on the ellipsoid E

.Ifλ

< 0, E

is properly con-

tained in E

.Ifλ

> 0, then E

and E

are separated, or E

contains E

. Otherwise,

0 ∈[λ

, λ

]and the two ellipsoids intersect. Illustrations in two dimensions are shown

in Figures 7.7, 7.8, and 7.9, but apply equally well to the three-dimensional case.

The problem can be formulated as a constrained optimization that is solved

by the method of Lagrange multipliers (Section A.9.3). Optimize Q

(X) subject

to the constraint Q

(X) = 0. Deﬁne F(X, t) = Q

(X) + tQ

(X). Differentiating

with respect to the X-components yields



∇F =



∇Q

+ t



∇Q

. Differentiating with

respect to t yields ∂F /∂t = Q

. Setting the t-derivative equal to zero reproduces the

constraint Q

=0. Setting the X-derivative equal to zero yields



∇Q



∇Q



0 for

some t. Geometrically this means the gradients are parallel.

Note that



∇Q

= 2A

X + B

,so



0 =



∇Q

+ t



∇Q

= 2(A

+ tA

)X + (B

+ tB

)

Formally solving for X yields

X =−

+ tA

)

−1

+ tB

) =

δ(t)

Y(t)

where A

+ tA

is a matrix of linear polynomials in t and δ(t) is its determinant, a

cubic polynomial in t. The components of Y(t)are cubic polynomials in t. Replacing

this in Q

(X) = 0 yields

Y(t)

Y(t)+ δ(t)B

Y(t)+ δ(t)

= 0

a sixth-degree polynomial in t. The roots can be computed, the corresponding values

of X computed, and Q

(X) evaluated. The minimum and maximum values are

stored as λ

and λ

, and the earlier comparisons with zero are applied.

Finding Intersections

The quadratic equations for the ellipsoid can be written as quadratic polynomials in

z whose coefﬁcients are functions of x and y: Q

(x, y, z) = α

(x, y) + α

(x, y)z +

(x, y)z

and Q

(x, y, z) =β

(x, y) +β

(x, y)z +β

(x, y)z

. Using the method of

606 Chapter 11 Intersection in 3D

elimination discussed in Section A.2, the two equations have a common z-root if and

only if the B

ezout determinant is zero,

R(x, y) = (α

− α

)(α

− α

) − (α

− α

)

= 0 (11.38)

The polynomial R(x, y) has degree at most 4. If (x, y) is a solution to R(x, y) = 0,

the common z-root is

z =

− α

If Equation 11.38 has any solutions, there must be at least one solution (x, y) that

is closest to the origin. This problem can be set up as a constrained minimization:

Minimize x

+ y

subject to the constraint R(x, y) = 0. Applying the method of

Lagrange multipliers (see Section A.9.3), deﬁne F(x, y, t) =x

+tR(x, y).The

derivatives are

, F

) = (2x +tR

,2y +tR

, R)

where the variable subscripts indicate partial derivatives with respect to those vari-

ables. The equation F

=0 just reproduces the constraint R = 0. The equations F

0 and F

= 0 yield 2x + tR

= 0 and 2y +tR

= 0. Eliminating t produces another

polynomial equation

S(x, y) = yR

− xR

= 0. (11.39)

The polynomial S(x, y) also has degree at most 4.

We now have two polynomial equations in two unknowns, R(x, y) = 0 and

S(x, y) = 0. Each polynomial can be written as polynomials in y whose coefﬁcients

are polynomials in x: R(x, y) =



i=0

(x)y

and S(x, y) =



i=0

(x)y

.The

ezout matrix for the two polynomials in y is the 4 × 4 matrix M = [M

] with

min(4,7−i−j)



k=max(4−j ,4−i)

k,7−i−j−k

for 0 ≤i ≤ 3 and 0 ≤j ≤3, with w

i,j

=α

−α

for 0 ≤i ≤ 4 and 0 ≤ j ≤4. In

expanded form,

M =







4,3

4,2

4,1

4,0

4,2

3,2

+ w

4,1

3,1

+ w

4,0

3,0

4,1

3,1

+ w

4,0

2,1

+ w

3,0

2,0

4,0

3,0

2,0

1,0







11.9 Quadric Surfaces 607

The degrees of α

and β

are at most 4 −i. The degree of w

i,j

is at most 8 −i −j .The

ezout determinant is D(x) = det(M(x)), a polynomial of degree at most 16 in x.

The roots of D(x) = 0 are computed. For each root ¯x, the coefﬁcients of f(y)

are computed and the y-roots for R( ¯x, y) = 0 are computed. If ¯y is such a root,

the pair ( ¯x, ¯y) is tested to make sure S(¯x, ¯y) = 0. If so, we have found a point of

intersection for the two ellipsoids. If the point is an isolated one, the two ellipsoids are

tangent at that point. The point is isolated if ∇Q

( ¯x, ¯y) and ∇Q

( ¯x, ¯y) are parallel. A

simple veriﬁcation that the cross product of the gradient vectors is the zero vector will

sufﬁce. If the point is not isolated, the intersection set will consist of a closed curve.

A differential equation solver can be used to traverse the curve:

= R

(x, y),

=−R

(x, y), (x(0), y(0)) = ( ¯x, ¯y) (11.40)

The vector (R

, R

) is normal to the level curve deﬁned by R = 0, so the vector

, −R

) is tangent to the level curve. The differential equations just specify to

traverse the curve by following the tangent vector.

The main problem with the former algorithm is that numerically ﬁnding the roots

of a degree 16 polynomial can be an ill-conditioned problem. An alternative is to use

an iterative search by setting up a system of differential equations that allows you to

walk along one ellipsoid in search of a point of intersection with the other ellipsoid.

The search will either ﬁnd a point or determine that there is none.

Start with a point X

on ellipsoid E

,soQ

) = 0. If Q

) = 0, we already

have a point of intersection. If Q

)<0, then X

is inside the ellipsoid E

.The

idea is to walk tangentially along the ﬁrst ellipsoid while increasing the value of Q

to zero. In space, the direction of largest increase of Q



∇Q

. This vector is normal

to ellipsoid E

but is usually not tangent to the ellipsoid E

. The vector must be

projected onto the tangent space of E

by subtracting the contribution by



∇Q

.The

path on E

with the largest increase in Q

locally is determined by



∇Q

−



∇Q



∇Q





∇Q





∇Q

, X(0) = X

In the event that Q

)>0, the tangent direction must be reversed so that Q

decreased as rapidly as possible to zero. The differential equations for this case are

=−



∇Q



∇Q



∇Q





∇Q





∇Q

, X(0) = X

Regardless of whether the ellipsoids intersect, eventually the traversal will lead to

a point for which the gradients are parallel. In this case the right-hand side of the

differential equation reduces to the zero vector. The length of the right-hand side

vector can be used as a termination criterion in the numerical solver. Another concern

is that the numerical solver will produce a new position from an old one and, because

608 Chapter 11 Intersection in 3D

of numerical error, the new position might not be on the ﬁrst ellipsoid. A correction

can be made to adjust the new position so that it is on the ﬁrst ellipsoid. The corrected

value can be used to generate the next iterate in the solver.

Once a point X

=X(T ) at some time T>0 for which Q

) =0, the 2D level

curve traversal of Equation 11.40 can be applied. However, it is possible to traverse the

curve of intersection directly in 3D. A tangent vector for the curve is perpendicular

to both



∇Q

and



∇Q

. The system of equations to solve is



∇Q



∇Q

, X(0) = X

Regardless of which system of differential equations is used to traverse the intersec-

tion curve, some type of stopping criterion must be implemented that detects the

traversal has reached the point X

at which the traversal originated.

11.10 Polynomial Surfaces

In this section, we brieﬂy discuss the general problem of computing the intersection

of two polynomial surfaces and point you to some of the wealth of literature address-

ing this difﬁcult and important problem.

The problem of surface-surface intersections (SSIs) arises quite frequently in

many computer graphics applications—modeling, ﬁnite-element mesh generation,

tool path speciﬁcation, scientiﬁc visualization, interference and feature detection,

and so on. SSIs are obviously very signiﬁcant in boundary-rep geometric modeling

applications, and the intersection of algebraic and NURBS surfaces is considered to

be a fundamental consideration in the integration of geometric and solid modeling

systems. Figure 11.59 shows two B-spline surfaces intersecting in two closed loops

and one open curve. Figure 11.60 shows the intersection curves in the parameter

space of one of the surfaces.

A very large body of work, stretching back several decades, addresses the problems

associated with SSI. Recent surveys can be found in Patrikalakis (1993), Pratt and

Geisow (1986), and Hoffman (1989). SSI algorithms are typically classiﬁed into four

categories: subdivision methods, lattice evaluation, analytic methods, and marching

methods. Various hybrids involving several of these methods have been proposed as

well.

11.10.1 Subdivision Methods

The core idea here is to (recursively) decompose the problem into smaller and sim-

pler problems; a trivial example would be to recursively subdivide the surfaces into

bilinear patches, which would then be intersected. Subdivision continues until some

stated criteria are reached, at which point the individual curves are pieced together

to form one or more contiguous curves. Typically, subdivision control is based on

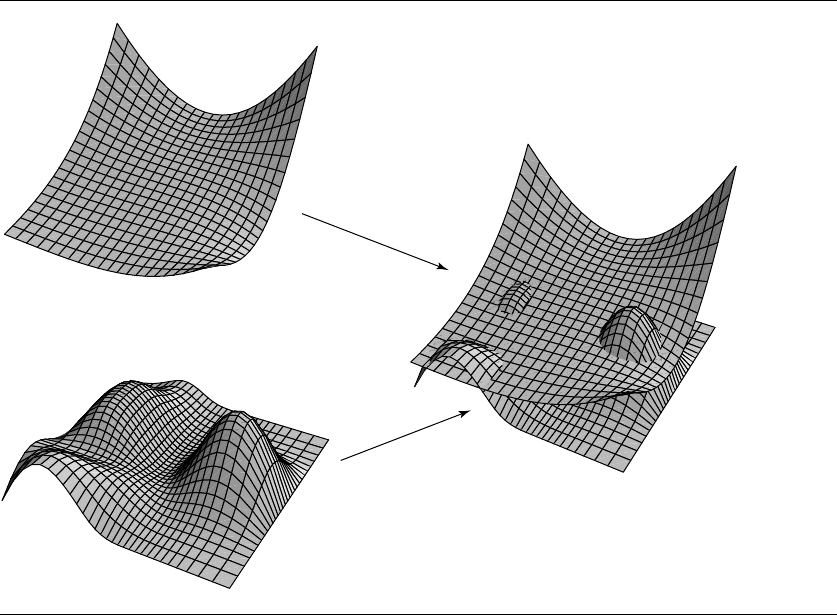
11.10 Polynomial Surfaces 609

Figure 11.59 Intersection of two B-spline surfaces.

geometric properties of the control polygon—for example, variation-diminishing

property, convex hull, and so on (Lane and Riesenfeld 1980; Lasser 1986). In the limit,

subdivision methods converge on the actual intersection curve, but tend to produce

very large amounts of data and run quite slowly. Attempts to reduce these problems

by constraining the level of subdivision can improve the speed, but risk missing small

features such as loops, or miss or incorrectly connect singularities.

11.10.2 Lattice Evaluation

In this approach, the surface intersection problem is reduced to a series of problems

of lower geometric complexity, such as curve-surface intersections (Rossignac and

Requicha 1987). Like the subdivision methods, lattice approaches tend to be slow

and also exhibit problems with respect to missing loops and singularities.

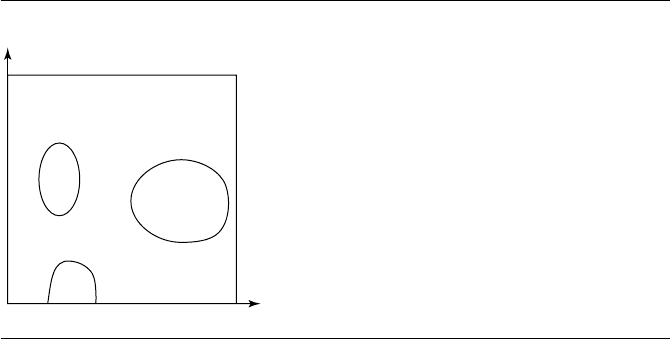
610 Chapter 11 Intersection in 3D

Figure 11.60 Intersection curves in one surface’s parameter space.

11.10.3 Analytic Methods

The approach here is to attempt to ﬁnd an explicit representation of the intersection

curve. This has found success only in a limited area—generally cases in which the

intersection curve is of low degree (Sederberg 1983; Sarraga 1983) and/or is limited

to special cases or speciﬁc types of surfaces (Piegl 1989; Miller 1987; Miller and

Goldman 1992, 1995) using a geometric (as opposed to strictly algebraic) approach.

11.10.4 Marching Methods

Also known as curve tracing, the basic idea behind marching is this (Hoffman 1989,

206):

Atapointp on the intersection, a local approximation of the curve is constructed;

for example, the curve tangent at p. By stepping along the approximation a spe-

ciﬁc distance, we obtain an estimate of the next curve point that we then reﬁne

using an iterative method.

Tracing/marching methods seem to be the most widely used (Barnhill and Kersey

1990; Farouki 1986; Bajaj et al. 1989). The reasons cited (Krishnan and Manocha

1997) are their (relative) ease of implementation and their generality (they can handle

such things as offsets and blends, which are particularly important in CAD appli-

cations). Two major issues arise in this approach: ﬁrst, the starting points for the

intersection curves must be identiﬁed. Intersection curves, as we have seen, may be

boundary segments or closed loops, and degeneracies such as singularities may be

present. Boundary segment start points can be identiﬁed by curve-surface intersec-

11.11 The Method of Separating Axes 611

tion methods (Sederberg and Nishita 1991). Detection of closed loops has proven

more problematic; most approaches use Gauss maps for bounding and simply sub-

divide the surface until “sufﬁcient conditions for the non-existence of loops are sat-

isﬁed” (Krishnan and Manocha 1997).

The second major issue for tracing methods is this: once the start point(s) are

identiﬁed, most algorithms use a variant of Newton’s method to do the actual tracing.

However, in practice the step size must be kept very small to avoid what is referred to

as component jumping. The result is that this operation can be very slow. Relatively

more recent work by Krishnan and Manocha (1997) has addressed these signiﬁcant

issues with a good deal of success.

11.11 The Method of Separating Axes

The concept of separating axes in three dimensions is identical to that of two dimen-

sions in Section 7.7. Two stationary convex objects do not intersect if there exists

a line for which the projections of the objects onto that line do not intersect. The

method applies to moving convex objects, and the geometric queries test-intersection

and ﬁnd-intersection can be formulated just as in two dimensions.

11.11.1 Separation of Stationary Convex Polyhedra

In two dimensions we concentrated our efforts on convex polygons. In three dimen-

sions we focus on convex polyhedra, but particular attention must be given to the

case when both polyhedra are really planar polygons. For a pair of convex polyhedra,

only a ﬁnite set of direction vectors needs to be considered for separation tests. This

is analogous to the two-dimensional problem with convex polygons, but we do not

provide a proof of the claim in three dimensions. The intuition, however, is similar

to that of convex polygons in two dimensions. If the two polyhedra are just touching

with no interpenetration, the contact is one of face-face, face-edge, face-vertex, edge-

edge, edge-vertex, or vertex-vertex. The set of potential directions that capture these

types of contact includes the normal vectors to the faces of the polyhedra and vectors

generatedbyacrossproductoftwoedges,onefromeachpolyhedron.

Let C

for j = 0, 1 be the convex polyhedra with vertices {V

(j)

}

−1

i=0

, edges

{e

(j)

}

−1

i=0

, and faces {F

(j)

}

−1

i=0

. Let the faces be planar convex polygons whose ver-

tices are counterclockwise ordered as you view the face from outside the polyhedron.

Outward-pointing normal vectors can be stored with each face as a way of storing the

orientation. We assume that each face has queries that allow access to the face normal

and to vertices on the face. We assume that each edge has a query that allows access

to its vertices.

The pseudocode for testing for intersection of two convex polyhedra, both having

positive volume (so L

≥ 4), is similar to the direct implementation in 2D:

612 Chapter 11 Intersection in 3D

bool TestIntersection(ConvexPolyhedron C0, ConvexPolyhedron C1)

{

// test faces of C0 for separation

for (i = 0; i < C0.L; i++) {

D = C0.F(i).normal;

ComputeInterval(C0, D, min0, max0);

ComputeInterval(C1, D, min1, max1);

if (max1 < min0 || max0 < min1 )

return false;

}

// test faces of C1 for separation

for (j = 0; j < C1.L; j++) {

D = C1.F(j).normal;

ComputeInterval(C0, D, min0, max0);

ComputeInterval(C1, D, min1, max1);

if ( max1 < min0 || max0 < min1)

return false;

}

// test cross products of pairs of edges

for (i = 0; i < C0.M; i++) {

for (j = 0; j < C1.M; j++) {

D = Cross(C0.E(i), C1.E(j));

ComputeInterval(C0, D, min0, max0);

ComputeInterval(C1, D, min1, max1);

if (max1 < min0 || max0 < min1)

return false;

}

return true;

}

void ComputeInterval(ConvexPolyhedron C, Point D, float& min, float& max)

{

min = Dot(D, C.V(0)); max = min;

for (i = 1; i < C.N; i++) {

value = Dot(D, C.V(i));

if (value < min) min = value; else max = value;

}

11.11 The Method of Separating Axes 613

The asymptotically better algorithm for ﬁnding the extreme points of a convex

polygon in 2D does have a counterpart in 3D. Given n vertices, it is possible to ﬁnd

extreme points in O(log n) time (Kirkpatrick 1983; Dobkin and Kirkpatrick 1990). A

well-written presentation of the algorithm is provided in O’Rourke (1998). However,

for applications that have small n or those that have polyhedra with a lot of symmetry,

typically oriented bounding boxes, the time spent implementing, testing, and debug-

ging this algorithm is probably not justiﬁed, especially if the constant in the O(log n)

algorithm is sufﬁciently large compared to the constant in the straightforward O(n)

algorithm.

The

TestIntersection pseudocode listed earlier has problems when both convex

polyhedra are convex polygons in the same plane. In this case the common normal

vector is not a separating direction. The cross product of any pair of edges is again a

normal vector to the plane, so it cannot separate the two polygons. In fact, coplanar

convex polygons in 3D must be handled with the algorithm for convex polygons

in 2D. All that we need in 3D are vectors that are in the plane of the polygons

and are perpendicular to the appropriate edges. If n is a plane normal and if e is

an edge vector for a polygon, then n ×e is a potential separating direction. The

pseudocode is

bool TestIntersection(ConvexPolygon C0, ConvexPolygon C1)

{

// test normal of C0 for separation

D = C0.normal;

ComputeInterval(C0, D, min0, max0);

ComputeInterval(C1, D, min1, max1);

if (max1 < min0 || max0 < min1)

return false;

Point N0xN1 = Cross(C0.normal, C1.normal);

if (N0xN1 != 0) {

// polygons are not parallel

// test normal of C1 for separation

D = C1.normal;

ComputeInterval(C0, D, min0, max0);

ComputeInterval(C1, D, min1, max1);

if (max1 < min0 || max0 < min1)

return false;

// test cross products of pairs of edges

for (i = 0; i < C0.M; i++) {

for (j = 0; j < C1.M; j++) {

D = Cross(C0.E(i), C1.E(j));

ComputeInterval(C0, D, min0, max0);

ComputeInterval(C1, D, min1, max1);