Schneider P., Eberly D.H. Geometric Tools for Computer Graphics

Подождите немного. Документ загружается.

554 Chapter 11 Intersection in 3D

nˆ

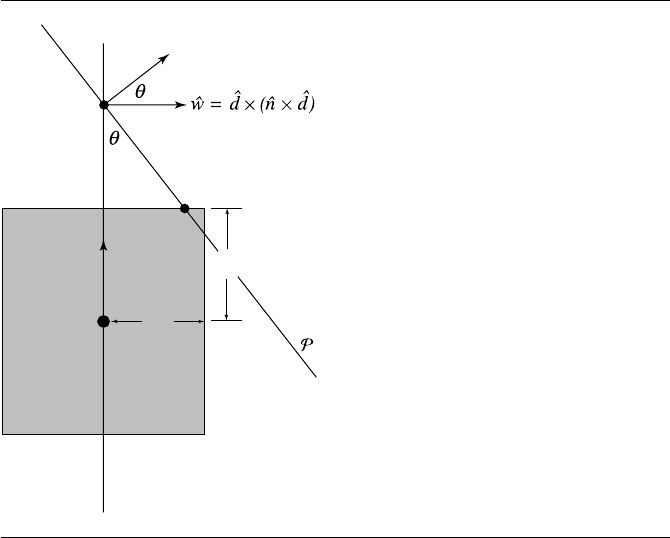
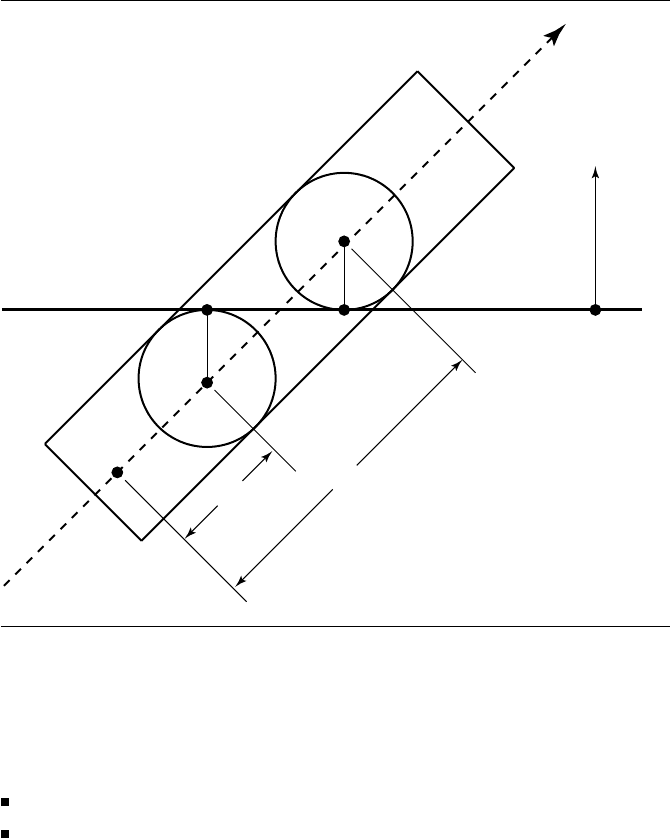
Figure 11.36 Edge-on view of plane-cylinder intersection.

All of the cases but the last are fairly trivial. Determining whether or not the

plane is parallel or perpendicular to the cylinders’s axis involves only a dot product.

Computing the distance between the cylinder’s centerpoint C and the plane is simple

and inexpensive (see Section 10.3.1). Computing the intersection of the plane and

the cylinder’s axis is inexpensive as well (see Section 11.1.1). Only the last case has

any expense associated with it, and so the tests should be done in the order discussed.

The last case is illustrated in Figure 11.36. The edge-on view is not simply a dia-

grammatic convenience—the method for determining whether or not an intersection

exists is done in a plane perpendicular to P and going through C. The rest is basic

trigonometry.

If I

is the intersection of P and the axis of the cylinder, then if the point I

is closer to the axis than r (the radius of the cylinder), we have an intersection.

The plane P

⊥

perpendicular to P and going through C is parallel to

d, and so its

normal is

ˆn ×

11.7 Planar Components and Quadric Surfaces 555

WedeﬁneavectorinP

⊥

that is perpendicular to

ˆw =

d × ( ˆn ×

The angle θ between ˆn and ˆw is

cos(θ) =ˆn ·w

We also know the distance a:

a =I

− C−h

By the deﬁnition of the cosine function, we know

cos(θ) =

Substituting, we get

ˆn ·w =

I

− C−h

and so

c =

I

− C−h

ˆn ·w

Invoking the Pythagorean Theorem, we have

+ b

= c

(I

− C−h)

+ b



I

− C−h

ˆn ·w





I

− C−h

ˆn ·w



− (I

− C−h)

and so if b

≤ r

, we have an intersection; otherwise, not.

Intersection with an Inﬁnite Cylinder

The general plane-quadric intersection formulation given in Section 11.7 yields an

implicit equation of a quadratic curve in terms of parameters of the plane. Such

representations are not very convenient. In the case of the intersection of a plane and

556 Chapter 11 Intersection in 3D

ˆv

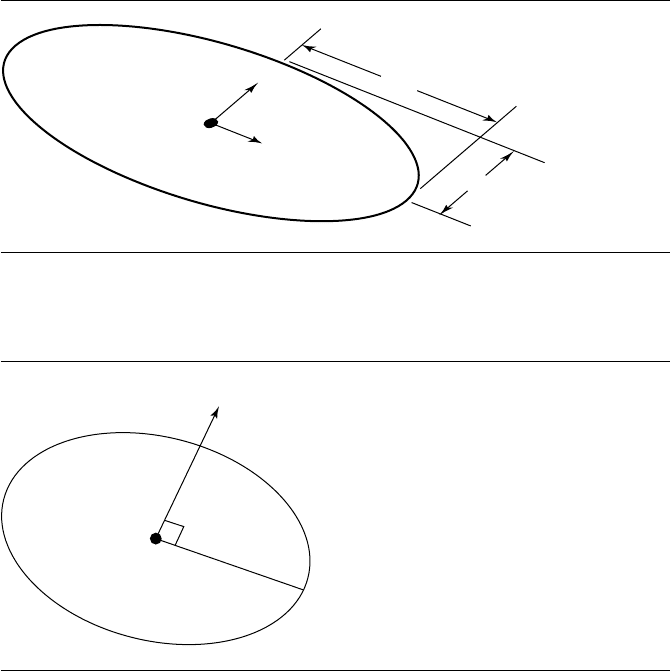
Figure 11.37 Ellipse in 3D.

ˆn

Figure 11.38

Circle in 3D.

a cylinder, we can get an ellipse or circle that ought to be described in a more direct

geometric fashion; by this we mean that an ellipse should be deﬁned by a centerpoint

C, major and minor axes ˆu and ˆv, and major and minor radii r

and r

, as shown in

Figure 11.37, and a circle should be deﬁned as a centerpoint C, normal to the plane

ˆn, and radius r, as shown in Figure 11.38.

As seen in Figure 11.35, the intersection of a plane with an inﬁnite cylinder can be

a single line, two lines, a circle, or an ellipse. The ﬁrst three of these are special cases

that occur only when the plane and cylinder are at one of two special angles relative

to one another, and so the ellipse may be considered to be the typical case.

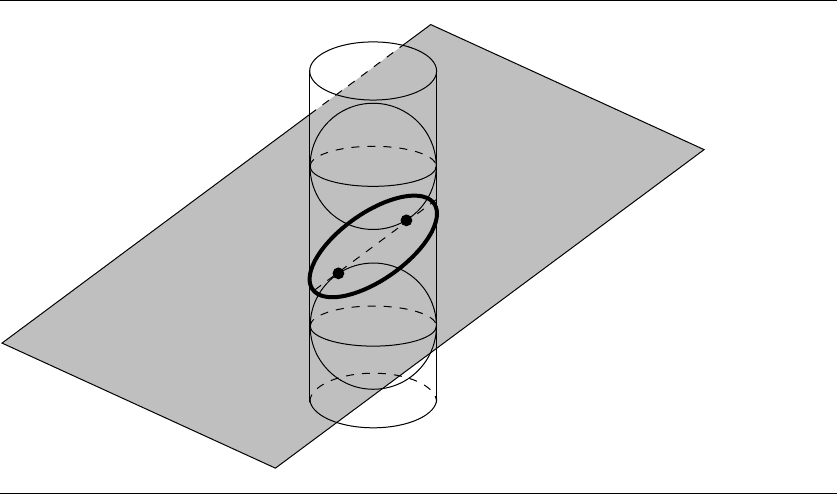
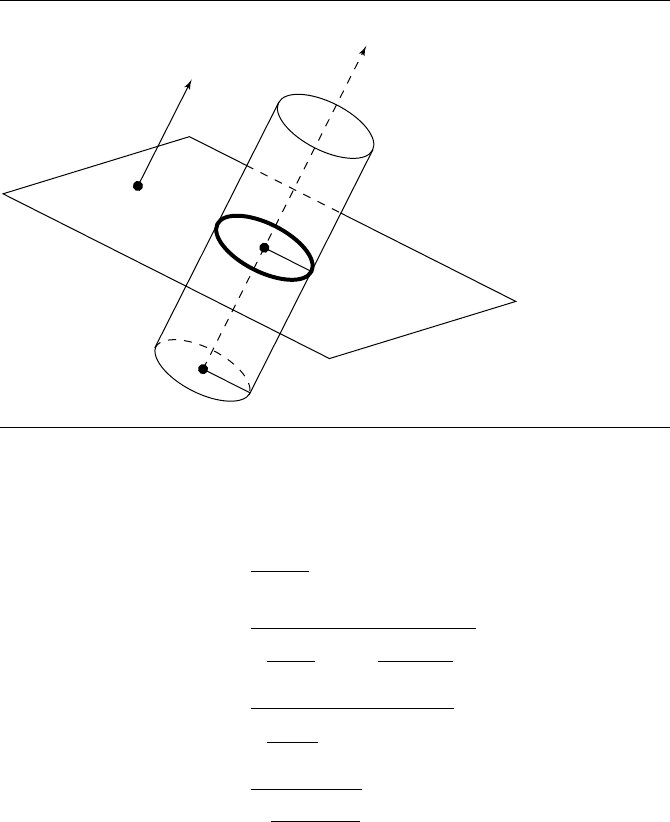
That the general intersection between a cylinder and a plane is an ellipse was

ﬁrst shown by Germinal Pierre Dandelin (1794–1847). Consider a cylinder and a

11.7 Planar Components and Quadric Surfaces 557

Figure 11.39 Dandelin’s construction.

plane intersecting; take a sphere whose radius is the same as the cylinder, and drop

it into the cylinder, and take a second sphere of the same radius, and push it up

into the cylinder from underneath. These two spheres will contact the intersecting

plane at two points, which are the two foci of the ellipse of intersection, as shown

in Figure 11.39. In addition, the minimum distance along the cylinder between the

circles at which the spheres are tangent to the cylinder is exactly twice the major

radius of the ellipse of intersection. A sketch of the proof of this can be found in Miller

and Goldman (1992), who describe how this fact can be used to ﬁnd the intersecting

ellipse in terms of the deﬁnition described earlier. We present that method here.

We assume the cylinder is represented by a base point B, axis ˆa, and radius r, and

the plane is represented by a point P and normal ˆn, so the implicit equation is

(X − P)·ˆn = 0 (11.21)

The cylinder, intersecting plane, and two spheres are shown in cross section in Fig-

ure 11.40.

558 Chapter 11 Intersection in 3D

ˆn

Figure 11.40 Cross section of a plane intersecting a cylinder, with the two spheres used to deﬁne

the intersecting ellipse. After Miller and Goldman (1992).

Miller and Goldman begin by noting two facts:

The two spheres’ centers C

and C

must be located along the axis of the cylinder.

The points of tangency are C ±r ˆn and constitute the foci of the ellipse of inter-

section.

As we know the radius of the spheres and the axis on which they lie, to complete their

deﬁnition we can simply determine their distances d

and d

from some ﬁxed point,

such as B, the base of the cylinder:

= B + d

ˆa

= B + d

ˆa

11.7 Planar Components and Quadric Surfaces 559

Thefociarethen

= B + d

ˆa +r ˆn

= B + d

ˆa −r ˆn

(11.22)

To determine the distances, we substitute Equation 11.22 into Equation 11.21, and

solve:

(P − B) ·ˆn − r

ˆa ·ˆn

(P − B) ·ˆn + r

ˆa ·ˆn

We would expect the center C of the ellipse of intersection to be on the axis ˆa of

the cylinder, and this can be shown by noting that C is precisely halfway between the

foci F

and F

C =

+ F

B + d

ˆa +r ˆn + B + d

ˆa −r ˆn

2B +(d

+ d

) ˆa

= B +

+ d

ˆa

= B +

(P −B)·ˆn−r

ˆa·ˆn

(P −B)·ˆn+r

ˆa·ˆn

ˆa

= B +

(P − B) ·ˆn

ˆa ·ˆn

ˆa

The point C is the intersection of the plane and the cylinder axis ˆa. The direction of

the major axis ˆu is parallel to F

− F

= B + d

ˆa +r ˆn − (B + d

ˆa −r ˆn)

= (d

+ d

) ˆa +2r ˆn

−2r

ˆa ·ˆn

ˆa +2r ˆn

560 Chapter 11 Intersection in 3D

Rearranging, we get

ˆa ·ˆn

−2r

− F

) =ˆa −( ˆa ·ˆn) ˆn

From this, Miller and Goldman observe that the direction of the major axis is the

component of ˆa perpendicular to ˆn. As stated earlier, the major axis is half the

distance between the circles of tangency between the spheres and the cylinder, which

is (as can be seen in Figure 11.40) |d

− d

|, giving us

− d

|ˆa ·ˆn|

The minor radius r

is the same as r, the radius of the cylinder. To show this, we

start with an observation: if we have an ellipse

= 1

where a>b, it can be shown that the foci are at ±

√

− b

. So, if we deﬁne c to be

the distance between the centerpoint C and the foci, the minor radius is



− c

The distance between the foci is 2c, and so the square of the distance is

=|F

− F

= 4r



( ˆa ·ˆn)

− 1



Taking the square root of both sides, and substituting cos(θ) =ˆa ·ˆv,weget

2c =|F

− F





cos

(θ)

− 1



= 2r tan(θ )

and so we have

11.7 Planar Components and Quadric Surfaces 561

ˆn

Figure 11.41 The intersection of a plane and a cylinder is a circle if the plane’s normal is parallel to

the cylinder’s axis.



− c





|ˆa ·ˆn|



−



2r tan(θ)







cos(θ)



− (r tan(θ))



1 − sin

(θ)

cos

(θ)

= r

We mentioned earlier that the conﬁgurations in which the intersection was a

circle or one or two lines are special cases, and we address these here. Clearly, if the

plane normal ˆn and the cylinder axis ˆa are parallel, then the intersection is a circle, as

shown in Figure 11.41.

If the plane normal ˆn is perpendicular to the cylinder axis ˆa, then we ﬁnd the

distance d between the cylinder’s base point B and the plane:

562 Chapter 11 Intersection in 3D

If |d| >r, then there are no intersections.

If |d|=r, then the intersection is one line B



+ t ˆa,whereB



is the projection of

B onto the plane.

If |d| <r, then the intersection consists of two lines:





− d

( ˆa ×ˆn) + t ˆa

The pseudocode is

boolean PlaneCylinderIntersection(Plane plane, Cylinder cylinder)

{

// Compute distance, projection of cylinder base point onto

// plane, and angle between plane normal and cylinder axis

d = PointPlaneDistance(cylinder.base, plane);

bPrime = cylinder.base-d*plane.normal;

cosTheta = Dot(cylinder.axis, plane.normal);

// Check angle between plane and cylinder axis to

// determine type of intersection

if (cosTheta < abs(epsilon)) {

// No intersection, or one or two lines. Check

// which it is by looking at distance from cylinder

// base point to plane

if (abs(d) == cylinder.radius) {

// Single line

line.base = bPrime;

line.direction = cylinder.axis;

return true;

}

if (abs(d) > cylinder.radius) {

// No intersection

return false;

}

// abs(d) < cylinder.radius, so two intersection lines

offset = Cross(cylinder.axis, plane.normal);

e = sqrt(cylinder.radius * cylinder.radius-d*d);

Line line1, line2;

line1.base = bPrime-e*offset;

11.7 Planar Components and Quadric Surfaces 563

line1.direction = cylinder.axis;

line2.base = bPrime+e*offset;

line2.direction = cylinder.axis;

return true;

}

// cosTheta != 0, so intersection is circle or ellipse

if (abs(cosTheta) == 1) {

// Circle

Circle circle;

circle.center = bPrime;

circle.normal = cylinder.axis;

circle.radius = cylinder.radius;

return true;

}

// abs(cosTheta) != 0 and abs(cosTheta) != 1, so ellipse

Ellipse ellipse;

ellipse.center = bPrime - (d / cosTheta) * cylinder.axis;

ellipse.u = cylinder.axis - cosTheta * plane.normal;

ellipse.v = Cross(plane.normal, ellipse.u);

rU = cylinder.radius / abs(cosTheta);

rV = cylinder.radius;

return true;

}

11.7.4 Plane and Cone

In this section we address the problem of the intersection of a plane and a cone, as

shown in Figure 11.42. There are actually quite a number of ways a cone and a plane

can intersect, eight of which are shown in Figure 11.43. Note that the intersections

are shown for a ﬁnite cone; an inﬁnite cone has fewer intersection conﬁgurations

because we don’t need to deal with the end caps. We give algorithms for intersection

detection of a plane and an inﬁnite cone and for a plane and a ﬁnite cone; the former

is somewhat simpler. In a later section, we’ll give an algorithm for computing the

intersection of a plane and an inﬁnite cone. These algorithms can be extended to a

ﬁnite cone by “clipping” the extent of the conic intersection curve or lines by the

planes containing the end caps.