Schneider P., Eberly D.H. Geometric Tools for Computer Graphics

Подождите немного. Документ загружается.

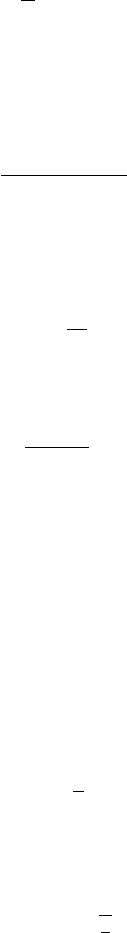
574 Chapter 11 Intersection in 3D

e = d tan(β)

= d tan(

− 2α)

= d cot(2α)

= d cot(π − 2θ)

=−d cot(2θ)

= d



tan(θ) − cot(θ)



By observing Figure 11.48, we see that the plane intersects the cone’s axis at a distance

2h from the cone’s vertex, and so we have

cos(θ) =

h =

2cos(θ )

We can now compute the parabola’s vertex and focus:

= V + d ˆn + e ˆv

F = V + h ˆa +r ˆv

We could easily use these formula for computing f , the focal length. However,

we can produce a more compact formula. Consider the triangle FCV

:itisaright

triangle with acute angle γ = π/2 − θ, and one leg is clearly r. The other leg we

denote as x. By trigonometry, we have

tan(γ ) =

But we know that r = d/2 (Equation 11.26), so we can rewrite the above as

tan(π/2 − θ) =

Recall from trigonometry these facts:

11.7 Planar Components and Quadric Surfaces 575

cos(

− α) = sin(α)

sin(

− α) = cos(α)

tan(α) =

sin (α)

cos(α)

We can rewrite this as

tan(θ)

x =

cot(θ )

The pseudocode for this case is the following (Miller and Goldman 1992):

float d = Dot(plane.base - cone.vertex, plane.normal);

float cosTheta = Dot(plane.normal, cone.axis);

float sinTheta = Sqrt(1 - cosTheta * cosTheta);

float tanTheta = sinTheta / cosTheta;

float cotTheta=1/tanTheta;

float e = d/2 * (tanTheta - cotTheta);

// Parabola is {V, u, v, f}

Vector v = Normalize(cone.axis - cosTheta * plane.normal);

Vector u = Cross(v, plane.normal);

Point V = cone.vertex+d*plane.normal+e*v;

float f = d/2 * cotTheta;

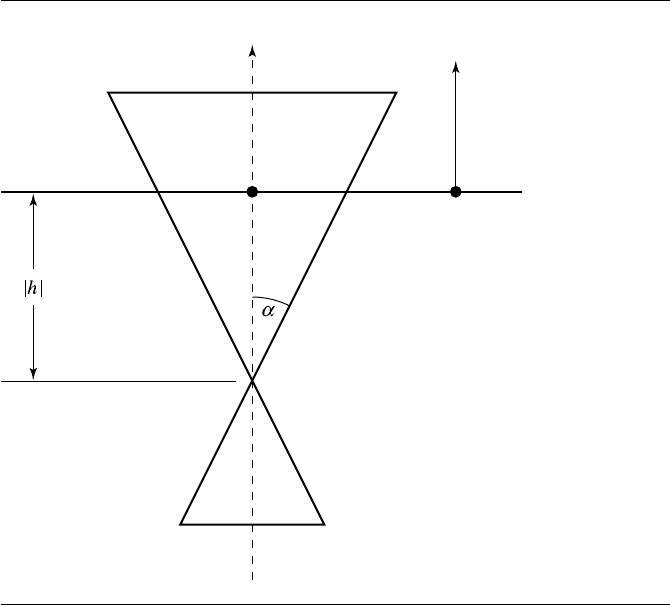
A circular intersection occurs when the plane normal ˆn is parallel to the cone axis

ˆa; that is, if |ˆn ·ˆa| <, as shown in Figure 11.49. Computing the circle is simple:

clearly, the center of the circle C is

C =V − h ˆa

where h is the (signed) distance from the plane to V , the cone vertex. The circle’s

normal is of course just the plane’s normal ˆn; the radius r can be computed with

simple trigonometry:

r =h tan(α)

576 Chapter 11 Intersection in 3D

ˆn

Figure 11.49 Circular curve intersection of plane and cone. After Miller and Goldman (1992).

The pseudocode is the following (Miller and Goldman1992):

// Signed distance from cone’s vertex to the plane

h = Dot(cone.vertex - plane.point, plane.normal);

circle.center = cone.vertex-h*plane.normal;

circle.normal = plane.normal;

circle.radius = Abs(h) * Tan(cone.alpha);

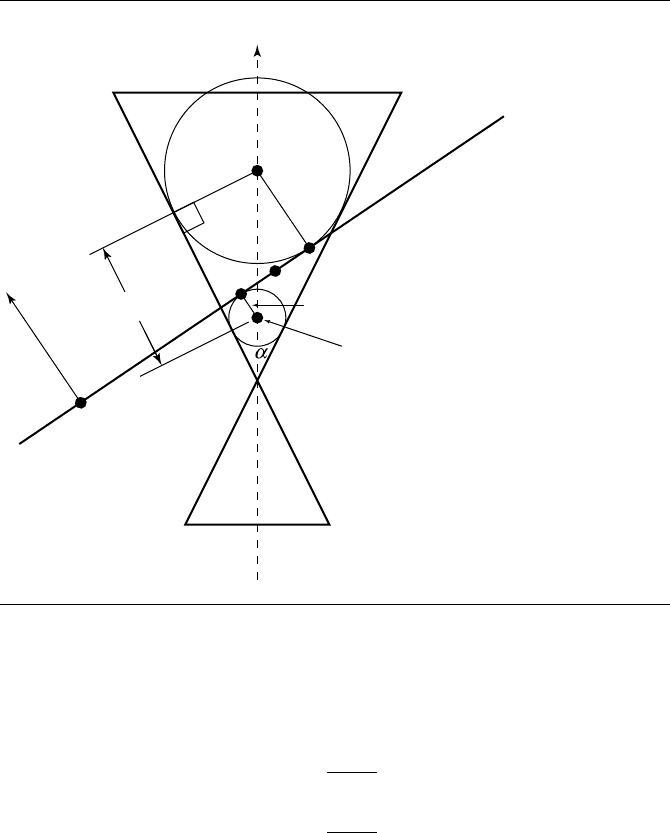
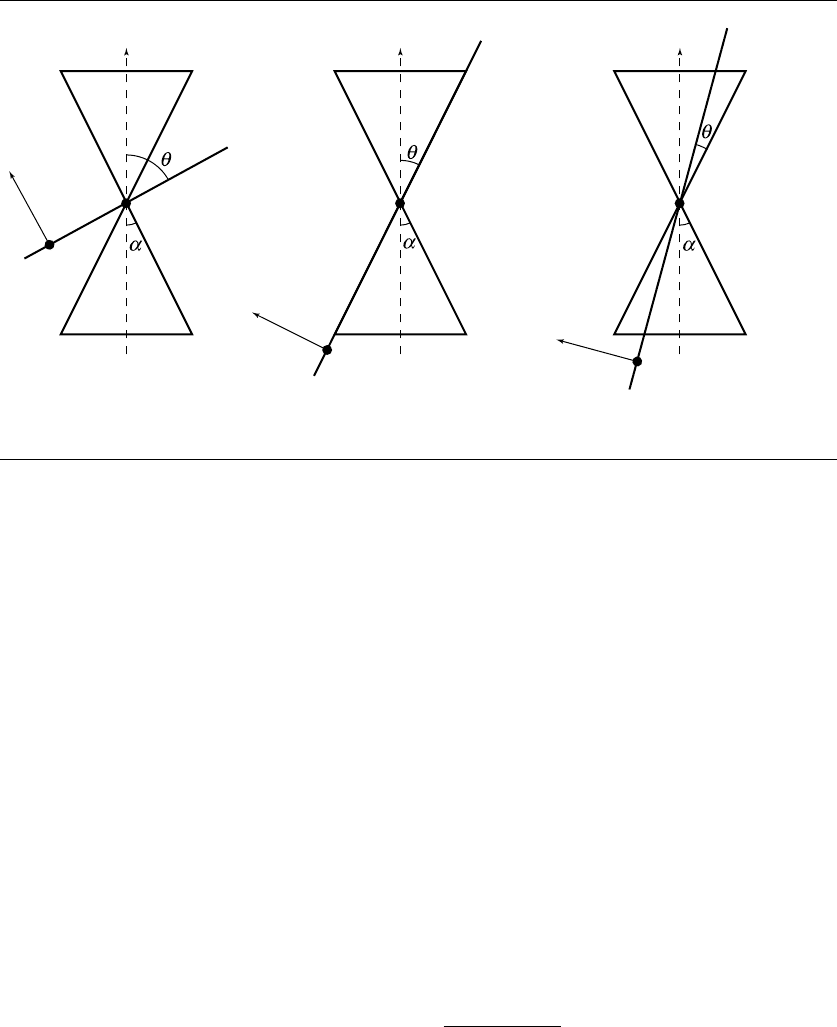
An elliptical intersection occurs when cos(θ) = sin(α), but when the plane nor-

mal ˆn and cone axis ˆa are other than parallel, as shown in Figures 11.50 and 11.51.

An ellipse is the intersection if cos(θ) > sin(α), and a hyperbola is the intersection if

cos(θ) < sin(α). To deﬁne the ellipse or hyperbola, we ﬁrst must determine the cen-

terpoint C. By deﬁnition, this is a point halfway between the foci: C =(F

+ F

)/2.

11.7 Planar Components and Quadric Surfaces 577

ˆn

Figure 11.50 Ellipse intersection of plane and cone. After Miller and Goldman (1992).

We h ave

= V +

sin(α)

− r

ˆn

= V +

sin(α)

− r

ˆn

where r

and r

are the two radii indicated by Equation 11.25. In the case of the ellipse,

the relationship between cos(θ) and sin(α) gives us positive values for r

and r

, and

the spheres lie on opposite sides of the plane, but on the same side of the cone; in the

case of the hyperbola, the relationship between cos(θ ) and sin(α) givesusanegative

value for r

and a positive value for r

, and the spheres lie on the same side of the

plane, but on the opposite sides of the cone.

578 Chapter 11 Intersection in 3D

ˆn

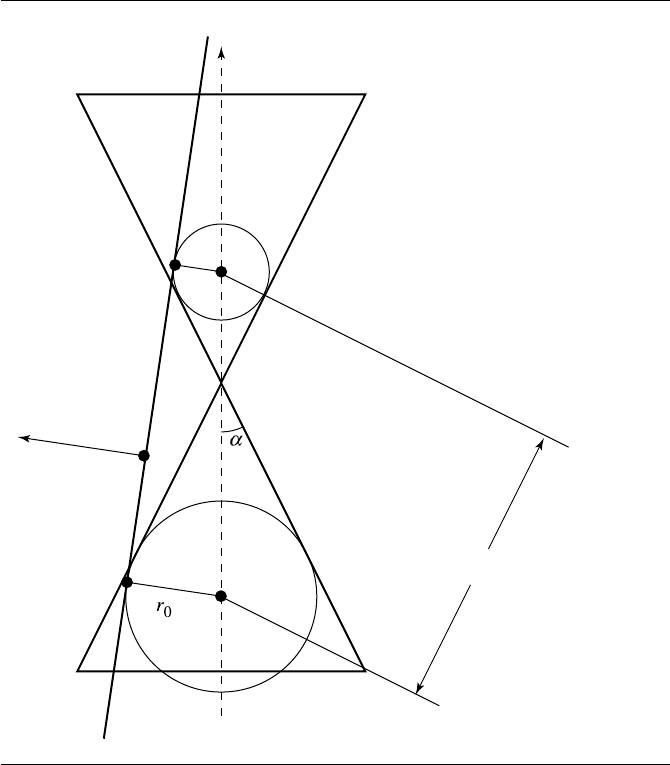
Figure 11.51 Hyperbola intersection of plane and cone. After Miller and Goldman (1992).

If we substitute the two versions of Equation 11.25 into the formula for the

foci, and then substitute this into the formula for the center, we get (after some

manipulation)

C =V + h cos(θ) ˆa − h sin

(α) ˆn

where

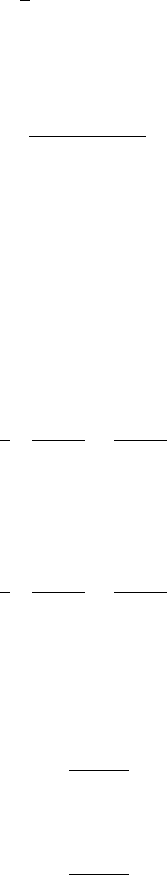
11.7 Planar Components and Quadric Surfaces 579

t = (P − V)·ˆn

b = cos

(θ) − sin

(α)

h =

Next come the directrix and focus vectors ˆu and ˆv. If we note that C, F

, and F

all lie in the plane parallel to the family of planes containing ˆa and ˆn, we see that

ˆu =

ˆa −cos(θ) ˆn

ˆa − cos(θ) ˆn

and so

ˆv =ˆn ·ˆu

The major and minor radii computations are a bit more involved, and here we

follow Miller and Goldman (1992) closely: recall that a characteristic of the tangent

spheres for the cone-plane intersection is that the major radius is half the distance

along a ruling between the circles of tangency between the spheres and the cone. For

the ellipse, this gives us



tan(α)

−

tan(α)



= h sin(α) cos(α)

and for the hyperbola



tan(α)

−

tan(α)



= h sin(α) cos(α)

Note that in both cases, r

is positive.

If we deﬁne d to be the (positive) distance between the center C and the foci, then

the minor radius of the ellipse is



− d

and for the hyperbola



− r

Again, note that in both cases, r

is positive.

580 Chapter 11 Intersection in 3D

The center C is halfway between the foci, so d is half the distance between the

foci, and thus

− F

) · (F

− F

)

If we substitute the formulas for F

and F

, and then substitute the formulas for

+ r

and r

− r

,weget

= t

sin(α)

√

The pseudocode is the following (Miller and Goldman 1992):

// Compute various angles

cosTheta = Dot(cone.axis, plane.normal);

cosThetaSqared = cosTheta * cosTheta;

sinAlpha = Sin(cone.alpha);

sinAlphaSquared = sinAlpha * sinAlpha;

cosAlpha = Sqrt(1 - sinAlphaSquared);

t = Dot(plane.point - cone.vertex, plane.normal);

b = cosThetaSquared - sinAlphaSquared;

h = t/b;

// Output is ellipse or hyperbola

center = cone.vertex+h*cosTheta * cone.axis

- h * sinAlphaSquared * plane.normal;

majorAxis = Normalize(cone.axis - cosTheta * plane.normal);

minorAxis = Cross(plane.normal, ellipse.u);

majorRadius = Abs(h) * sinAlpha * cosAlpha;

minorRadius=t*sinAlpha / Sqrt(Abs(b));

if (cosTheta > sinAlpha) {

// Ellipse

ellipse.center = center;

ellipse.majorAxis = majorAxis;

ellipse.minorAxis = minorAxis;

ellipse.majorRadius = majorRadius;

ellipse.minorRadius = minorRadius;

return ellipse;

} else {

// Hyperbola

hyperbola.center = center;

hyperbola.majorAxis = majorAxis;

11.7 Planar Components and Quadric Surfaces 581

Single point Single line

ˆn

ââ

Two lines

ˆn

Figure 11.52 Degenerate intersections of a plane and a cone. After Miller and Goldman (1992).

hyperbola.minorAxis = minorAxis;

hyperbola.majorRadius = majorRadius;

hyperbola.minorRadius = minorRadius;

return hyperbola;

}

Degenerate Plane-Cone Intersections

In order to distinguish between the three degenerate intersections, we consider the

angle between the cone’s axis ˆa and the plane’s normal ˆn, and its relationship to the

half-angle α deﬁning the cone. In each case, however, the plane contains the cone’s

vertex. The degenerate intersections are shown in Figure 11.52.

The intersection is a point if cos(θ) > sin(α).

The intersection is a single line if cos(θ) = sin(α). Clearly, the line passes through

the cone vertex V , and so this can be the base point of the intersection line. Since the

line lies in a plane parallel to the family of planes containing ˆv and ˆa, its direction is

ˆa −cos(θ) ˆn

ˆa − cos(θ) ˆn

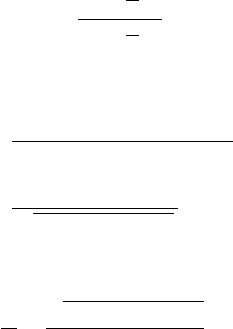
582 Chapter 11 Intersection in 3D

The intersection is two lines if cos(θ ) < sin(α). Again, the lines pass through the

cone vertex V , and so this can be the base point of the lines. As Miller and Gold-

man point out, these lines can be considered to be the asymptotes of a degenerate

hyperbola:

d =

ˆu ±

ˆv

ˆu ±

ˆv

From the previous section, we have

((P − V)·ˆn) sin(α) cos(θ)

sin

(α) − cos

(θ)

((P − V)·ˆn) sin(α)



sin

(α) − cos

(θ)

and thus



sin

(α) − cos

(θ)

cos(θ)

The pseudocode is the following (Miller and Goldman 1992):

// Assuming that Abs(Dist(cone.vertex, plane)) < epsilon...

if (Cos(theta) > Sin(alpha)) {

// Intersection is a point

intersectionPoint = cone.vertex;

} else if (Cos(theta) == Sin(alpha)) {

// Intersection is a single line

line.base = cone.vertex;

line.direction = Normalize(cone.axis - Cos(theta) * plane.normal);

} else {

// Intersection is two lines

u = Normalize(cone.axis - Cos(theta) * plane.normal);

v = Cross(plane.normal, u);

sinAlpha = Sin(alpha);

cosTheta = Cos(theta);

rVOverRU = Sqrt(sinAlpha * sinAlpha - cosTheta * cosTheta)

/ (1 - sinAlpha * sinAlpha);

line0.base = cone.vertex;

line0.direction = Normalize(u + rVOverRU * v);

line1.base = cone.vertex;

line0.direction = Normalize(u - rVOverRU * v);

}

11.7 Planar Components and Quadric Surfaces 583

11.7.5 Triangle and Cone

Let the triangle have vertices P

for 0 ≤i ≤ 2.TheconehasvertexV , axis direction

vector a, and angle θ between axis and outer edge. In most applications, the cone

is acute, that is, θ ∈ (0, π/2). This book assumes that, in fact, the cone is acute, so

cos θ>0. The cone consists of those points X for which the angle between X − V

and a is θ. Algebraically the condition is

a ·



X − V

X − V 



= cos θ

Figure 11.15 shows a 2D representation of the cone. The shaded portion indicates

the inside of the cone, a region represented algebraically by replacing “=” in the above

equation with “≥”.

To avoid the square root calculation X − V , the cone equation may be squared

to obtain the quadratic equation



a ·(X − V)



= (cos

θ)X − V 

However, the set of points satisfying this equation is a double cone. The original cone

is on the side of the plane a · (X −V)=0 to which a points. The quadratic equation

deﬁnes the original cone and its reﬂection through the plane. Speciﬁcally, if X is a

solution to the quadratic equation, then its reﬂection through the vertex, 2V − X,is

also a solution. Figure 11.16 shows the double cone.

To eliminate the reﬂected cone, any solutions to the quadratic equation must also

satisfy a · (X − V)≥ 0. Also, the quadratic equation can be written as a quadratic

form, (X −V)

M(X − V)= 0, where M = (aa

− γ

I) and γ = cos θ . Therefore,

X is a point on the acute cone whenever

(X − V)

M(X − V)= 0 and a · (X − V)≥ 0

Test Intersection

Testing if a triangle and cone intersect, and not having to compute points of in-

tersection, is useful for a couple of graphics applications. For example, a spotlight

illuminates only those triangles in a scene that are within the cone of the light. It is

useful to know if the vertex colors of a triangle’s vertices need to be modiﬁed due

to the effects of the light. In most graphics applications, if some of the triangle is il-

luminated, then all the vertex colors are calculated. It is not important to know the

subregion of the triangle that is in the cone (a result determined by a ﬁnd query).

Another example is for culling of triangles from a view frustum that is bounded by a

cone for the purposes of rapid culling.