Schneider P., Eberly D.H. Geometric Tools for Computer Graphics
Подождите немного. Документ загружается.

624 Chapter 11 Intersection in 3D
// face-face intersection
ConvexPolygon F0Moved = C0.F(Cfg0.index[0]) + tfirst * W0;
ConvexPolygon F1Moved = C1.F(Cfg1.index[1]) + tfirst * W1;
FindPolygonIntersection(F0Moved, F1Moved, I);
}
} else {
// polyhedra were initially intersecting
ConvexPolyhedron C0Moved = C0 + tfirst * W0;
ConvexPolyhedron C1Moved = C1 + tfirst * W1;
FindPolyhedronIntersection(C0Moved, C1Moved, I);
}
}
The semantics of the functions for the moved convex objects are clear from the
function names.
11.12 Miscellaneous
This section covers a variety of intersection problems that do not fit directly into the
previous categories of the chapter.
11.12.1 Oriented Bounding Box and Orthogonal Frustum
The separating axis method, discussed in Section 11.11, is used to determine if an
oriented bounding box (OBB) intersects an orthogonal frustum. This is useful for
accurate culling of an OBB bounding volume with respect to a view frustum.
The oriented bounding box is represented in symmetric form with center C;
axis directions ˆa
0
, ˆa
1
, and ˆa
2
; and extents e
0
, e
1
, and e
2
. The axis directions form a
right-handed orthonormal system. The extents are assumed to be positive. The eight
vertices of the box are C +
2
i=0
σ
i
e
i
ˆa
i
,where|σ
i
|=1 (eight choices on sign). The
three normal vectors for the six box faces are ˆa
i
for 0 ≤i ≤2. The three edge direction
vectors for the twelve box edges are the same set of vectors.
The orthogonal view frustum has origin E. Its coordinate axes are determined
by left vector
ˆ
l, up-vector ˆu, and direction vector
ˆ
d. The vectors in that order form
a right-handed orthonormal system. The extent of the frustum in the
ˆ
d direction is
[n, f ], w he re 0 <n<f. The view plane is assumed to be the near plane,
ˆ
d · (X −
E) = n. The far plane is
ˆ
d · (X − E) = f . The four corners of the frustum in the
near plane are E ± 4
ˆ
l ± µ ˆu + n
ˆ
d. The four corners of the frustum in the far plane
are E +(f/n)(±4
ˆ
l ±µ ˆu +n
ˆ
d). The five normal vectors for the six frustum faces are
ˆ
d for the near and far faces, ±n
ˆ
l −4
ˆ
d for the left and right faces, and ±n ˆu − 4
ˆ
d for
the top and bottom faces. The six edge direction vectors for the twelve frustum edges

11.12 Miscellaneous 625
are
ˆ
l and ˆu for the edges on the near and far faces, and ±4
ˆ
l ±µ ˆu + n
ˆ
d. The normal
and edge directions are not all unit length, but this is not necessary for the separation
axis tests.
Separating Axis Test
Two convex polyhedra do not intersect if there exists a line with direction m such that
the projections of the polyhedra onto the line do not intersect. In this case there must
exist a plane with normal vector m that separates the two polyhedra. Given a line, it
is straightforward to project the vertices of a polyhedron onto the line and compute
the bounding interval [λ
min
, λ
max
] for those projections. The two intervals obtained
from the two polyhedra are easily compared for overlap.
The more difficult problem is selecting a finite set of line directions such that
the intersection/nonintersection can be determined by separating axis tests using
only vectors in that set. For convex polyhedra it turns out that the set consisting
of face normals for the two polyhedra and vectors that are the cross product of
edges, one edge from each polyhedron, is sufficient for the intersection testing. If
polyhedron i has F
i
faces and E
i
edges, then the total number of vectors in the set
is F
0
+ F
1
+ E
0
E
1
. It is possible that some of the vectors formed by cross products
of edges are zero, in which case they do not need to be tested. This happens, for
example, with two axis-aligned bounding boxes. While the total number of vectors
is 3 + 3 +3 ∗3 =15, the set has only three nonzero vectors.
The oriented bounding box has F
0
=3 and E
0
=3. The orthogonal view frustum
has F
1
= 5 and E
1
= 6. The total number of vectors to test is 26. That set is
{
ˆ
d, ±n
ˆ
l −4
ˆ
d, ±n ˆu − µ
ˆ
d, ˆa
i
,
ˆ
l ׈a
i
, ˆu ׈a
i
, (±4
ˆ
l ±µ ˆu + n
ˆ
d) ׈a
i
}
The separating axes that are tested will all be of the form E +λ m,where m is in the
previously mentioned set. The projected vertices of the box have λ values m · (C −
E) +
2
i=0
σ
i
e
i
ˆa
i
,where|σ
i
|=1. Define d =m ·(C −E) and R =
2
i=0
e
i
|m ·ˆa
i
|.
The projection interval is [d − R, d + R].
The projected vertices of the frustum have λ values κ(τ
0
4 m ·
ˆ
l + τ
1
µ m ·ˆu + n m ·
ˆ
d),whereκ ∈{1, f/n} and |τ
i
|=1. Define p = 4|m ·
ˆ
l|+µ|m ·ˆu|. The projection
intervalis[m
0
, m
1
], w h er e
m
0
=
f
n
n m ·
ˆ
d − p
, n m ·
ˆ
d − p<0
n m ·
ˆ
d − p, n m ·
ˆ
d − p ≥0
and
m
1
=
f
n
n m ·
ˆ
d + p
, n m ·
ˆ
d + p>0
n m ·
ˆ
d + p, n m ·
ˆ
d + p ≤0
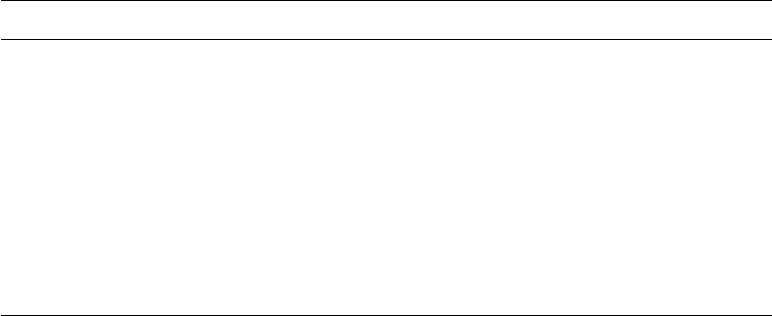
626 Chapter 11 Intersection in 3D
Table 11.5 Coefficients for the separating axis test
m m ·
ˆ
l m ·ˆu m ·
ˆ
d m · (C −E)
ˆ
d 001δ
2
±n
ˆ
l −4
ˆ
d ±n 0 −4 ±nδ
0
− 4δ
2
±n ˆu − µ
ˆ
d 0 ±n −µ ±nδ
1
− µδ
2
ˆa
i
α
i
β
i
γ
i
α
i
δ
0
+ β
i
δ
1
+ γ
i
δ
2
ˆ
l ׈a
i
0 −γ
i
β
i
−γ
i
δ
1
+ β
i
δ
2
ˆu ׈a
i
γ
i
0 −α
i
γ
i
δ
0
− α
i
δ
2
(τ
0
4
ˆ
l +τ
1
µ ˆu + n
ˆ
d) ׈a
i
−nβ
i
+ τ
1
µγ
i
nα
i
− τ
0
4γ
i
τ
0
4β
i
− τ
1
µα
i
[−nβ
i
+ τ
1
µγ
i
]δ
0
+
[nα
i
− τ
0
4γ
i
]δ
1
+
[τ
0
4β
i
− τ
1
µα
i
]δ
2
The box and frustum do not intersect if for some choice of m the two projection
intervals [m
0
, m
1
]and [d −R, d +R]do not intersect. The intervals do not intersect if
d +R<m
0
or d −R>m
1
. An unoptimized implementation will compute d, R, m
0
,
and m
1
for each of the 26 cases and test the two inequalities. However, an optimized
implementation will save intermediate results during each test and use them for later
tests.
Caching Intermediate Results
Effectively the potential separating axis directions will all be manipulated in the
coordinate system of the frustum. That is, each direction is written as m = x
0
ˆ
l +
x
1
ˆu + x
2
ˆ
d, and the coefficients are used in the various tests. The difference C − E
must also be represented in the frustum coordinates, say, C − E =δ
0
ˆ
l +δ
1
ˆu + δ
2
ˆ
d.
The coefficients are given in Table 11.5, where 0 ≤ i ≤2 and |τ
j
|=1 for 0 ≤ j ≤1.
The quantities α
i
, β
i
, γ
i
, and δ
i
are computed only when needed to avoid unnec-
essary calculations. Some products are computed only when needed and saved for
later use. These include products of n, 4,orµ with α
i
, β
i
, γ
i
,orδ
i
. Some terms that
include sums or differences of the products are also computed only when needed and
saved for later use. These include nα
i
± 4γ
i
, nβ
i
± µγ
i
, 4α
i
± µβ
i
, and 4β
i
± µα
i
.
11.12.2 Linear Component and Axis-Aligned Bounding Box
An axis-aligned bounding box (AABB) is simply a rectangular parallelepiped whose
faces are each perpendicular to one of the basis vectors. Such bounding boxes arise
frequently in spatial subdivision problems, such as in ray tracing or collision de-
11.12 Miscellaneous 627
d
P
(x
min
y
min
z
min
)
(x
max
y
max
z
max
)
Figure 11.61 Intersection of a linear component with an axis-aligned bounding box.
tection. One common way to specify such a box is to provide two points P
min
=
[
x
min
y
min
z
min
] and P
max
= [
x
max
y
max
z
max
], as shown in Figure 11.61.
This section considers the problem of finding the intersection of a linear compo-
nent and an AABB. You might consider that a bounding box consists of six rectangu-
lar faces, and simply intersect the linear component with each rectangle. You might,
in such an algorithm, exploit the fact that the rectangles’ edges are all parallel to a
basis vector, for the purpose of making the algorithm a bit more efficient.
An algorithm known as the “slabs method,” originated by Kay and Kajiya (1986)
and adapted by Haines (1989), can do a bit better, particularly if the linear component
is a ray, which is the most likely use (as in ray tracing and picking algorithms). The
basic idea is that intersection testing/calculation can be viewed as a clipping problem;
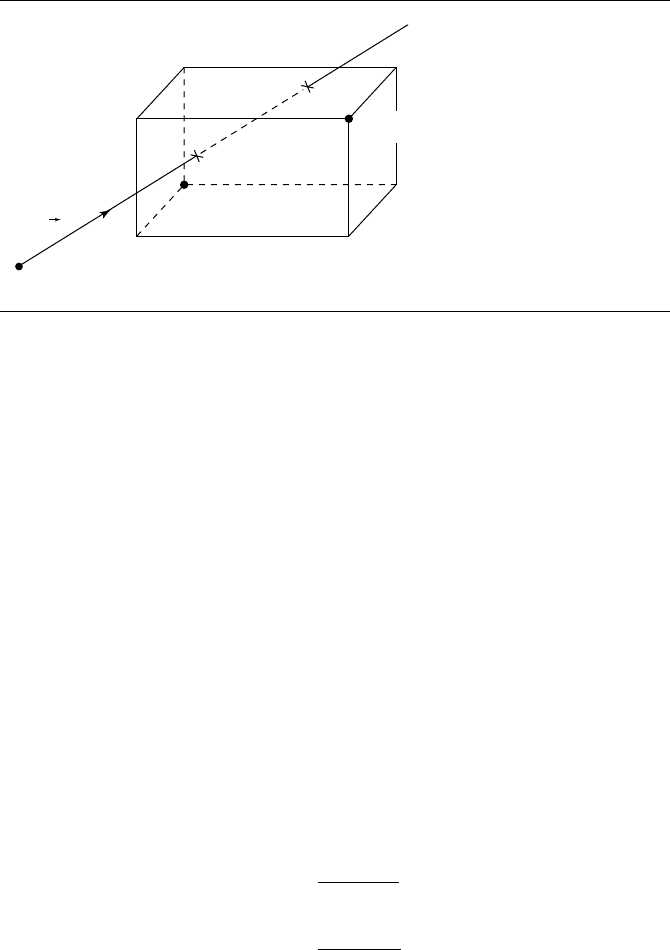
the method is called the “slabs” method because you can think of the AABB as
consisting of the intersection of three mutually perpendicular slabs of material, whose
boundaries are defined by each pair of opposing faces (see Figure 11.62).
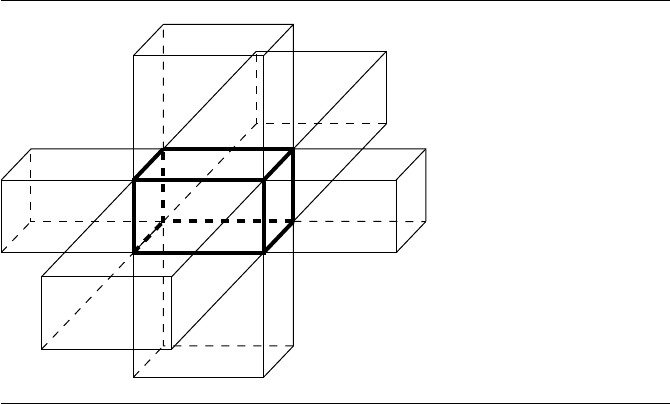
The basic clipping idea is illustrated in Figure 11.63, in which the ray P + t
ˆ
d
is clipped against the YZ planes at x
min
and x
max
. We can see that the points of
intersection, at parameter values t
0
and t
1
, are calculated as
t
0,x
=
x
min
− P
x
d
x
(11.41)
t
1,x
=
x
max
− P
x
d
x
(11.42)
Note that if the ray originated on the other side of the slab and intersected it, then the
nearest intersection would be t
1
instead of t
0
.
628 Chapter 11 Intersection in 3D
Figure 11.62 Axis-aligned box as the intersection of three “slabs.”
The pseudocode for the algorithm is
boolean RayIntersectAABB(Point P, Vector d, AABB box, float& tIntersect)
{
tNear = -INFINITY;
tFar = INFINITY;
foreach pair of planes {(XY_min, XY_max), (XZ_min, YZ_max), (YZ_min, YZ_max)} {
// Example shown for YZ planes
// Check for ray parallel to planes
if (abs(d.x) < epsilon) {
// Ray parallel to planes
if (P.x < box.xMin || P.x < box.xMax) {
return false;
}
}
// Ray not parallel to planes, so find parameters of intersections
t0 = (box.xMin - P.x) / d.x;
t1 = (box.xMax - P.x) / d.x;
// Check ordering
if (t0 > t1}) {
11.12 Miscellaneous 629
P
d
x
min
x
max
x
min
– P
x
P + t
1,x
d
ˆ
P + t
0,x
d
ˆ
ˆ
d
ˆ
x
Figure 11.63 Clipping a line against a slab.
// Swap them
tmp = t1;
t0 = t1;
t1 = tmp;
}
// Compare with current values
if (t0 > tNear) {
tNear = t0;
}
if (t1 < tFar) {
tFar = t1;
}
// Check if ray misses entirely
if (tNear > tFar) {
return false;
}
if (tFar < 0) {
return false;

630 Chapter 11 Intersection in 3D
}
}
// Box definitely intersected
if (tNear > 0) {
tIntersect = tNear;
} else {
tIntersect = tFar;
}
return true;
}
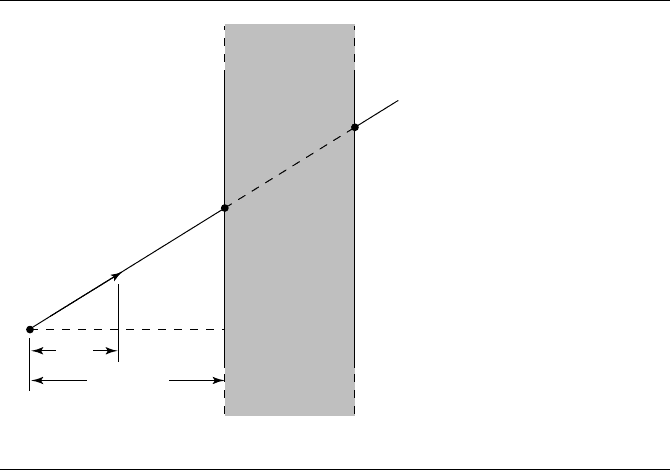
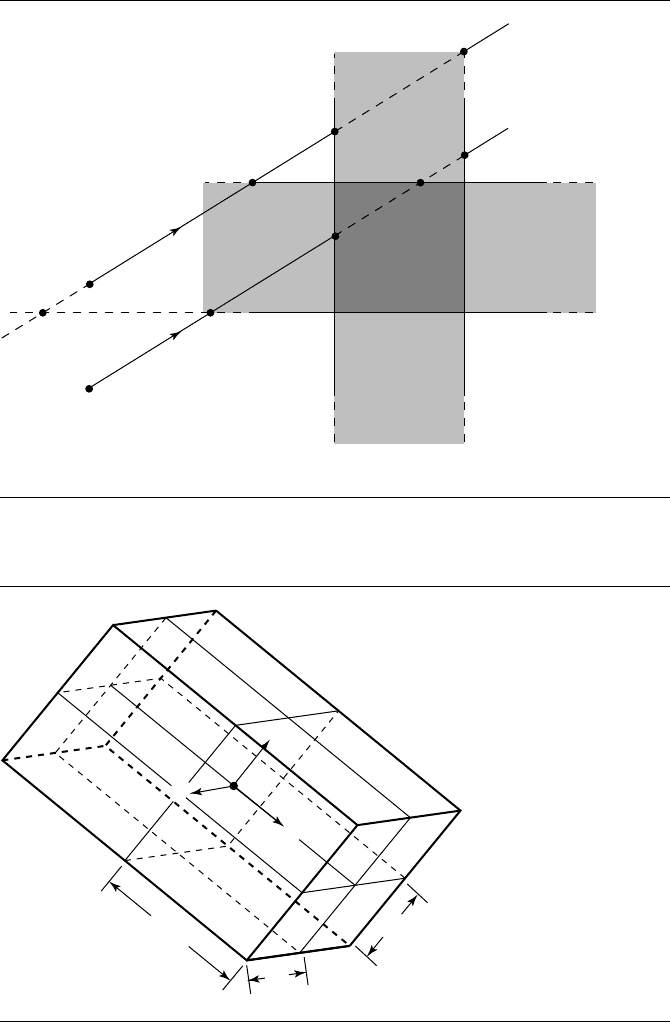
The reason this simple method works may not be readily apparent from the code,
but should be apparent from Figure 11.64. The lower ray intersects the box because
t
near
=t
0,x
<t
far
=t
1,y
and t
near
> 0. The upper ray misses because t
near
=t
0,x
>t
far
=
t
1,y
.
11.12.3 Linear Component and Oriented Bounding Box
An oriented bounding box is simply a bounding parallelepiped whose faces and
edges are not parallel to the basis vectors of the frame in which they’re defined. One
popular way to define them is to specify a (center) point C and orthonormal set of
basis vectors {ˆu, ˆv, ˆw}, which determines location and orientation, and three scalars
representing the half-width, half-height, and half-depth, as shown in Figure 11.65.
Note that an AABB can be defined using exactly this scheme by choosing the box’s
basis vectors to be exactly those of the space the box is defined; however, AABBs
are frequently computed by simply finding the maximum x, y, and z values of the
geometric primitives they bound, making the AABB definition used in the previous
section a bit more direct.
As an OBB is basically an AABB with a different orientation, you would expect
that the same basic algorithm can be used for computing intersections, and that
indeed is the case. M
¨
oller and Haines (1999) describe a version of the algorithm of
the previous section that works for OBBs.
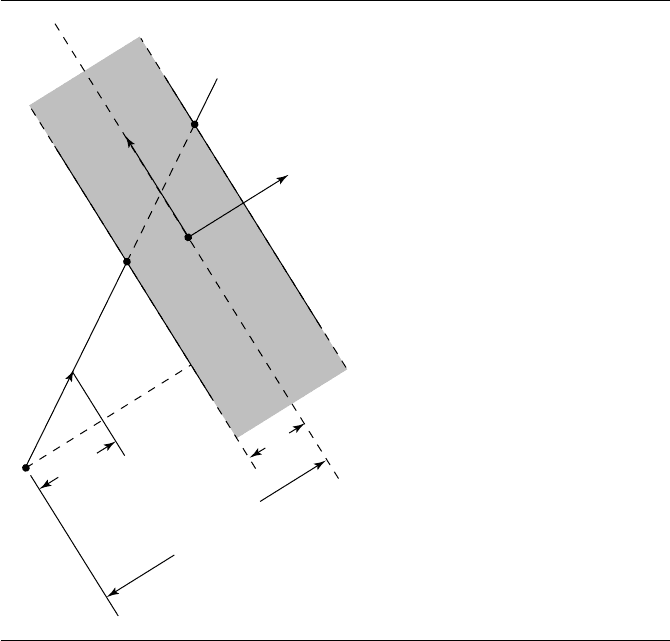
The distance calculation for oriented clipping is exactly analogous to that for slab
clipping (see Equation 11.41):
t
0,u
=
ˆu · (C − P)− h
u
ˆu ·
ˆ
d
t
1,u
=
ˆu · (C − P)+ h
u
ˆu ·
ˆ
d
as illustrated in Figure 11.66.
11.12 Miscellaneous 631
P
d
x
min
x
max
t
0,x
y
min
y
max
t
0,y
t
0,y
t
1,y
t
1,x
P
t
0,x
t
1,x
t
1,y
ˆ
d
ˆ
Figure 11.64 How slab clipping correctly computes ray-AABB intersection.
u
v
w
C
h
w
h
u
h
v
Figure 11.65 Specifying an oriented bounding box.
632 Chapter 11 Intersection in 3D
P
C
v
P + t
1,u
d
ˆ
P + t
0,u
d
ˆ
d
ˆ
d
ˆ
ˆ
û
û
•
(C – P)
h
u
û
•
Figure 11.66 Clipping against an “oriented slab.”
In the case of ray intersections, in most applications (ray tracing or interactive
picking, for example) only the closest intersection is required; if both (potential)
intersections are required, the following pseudocode can be modified to return both
tNear and tFar:
boolean RayIntersectOBB(Point P, Vector d, OBB box, float& tIntersect)
{
tNear = -INFINITY;
tFar = INFINITY;
foreach (i in {u, v, w}) {
// Check for ray parallel to planes
11.12 Miscellaneous 633
if (Abs(Dot(d, box.axis[i] < epsilon) {
// Ray parallel to planes
r = Dot(box.axis[i], box.C - P);
if (-r - box.halfLength[i]>0||-r+box.halfLength[i] > 0) {
// No intersection
return false;
}
}
r = Dot(box.axis[i], box.C - P);
s = Dot(box.axis[i], d);
// Ray not parallel to planes, so find parameters of intersections
t0 = (r + box.halfLength[i]) / s;
t1 = (r - box.halfLength[i]) / s;
// Check ordering
if (t0 > t1) {
// Swap them
tmp = t0;
t0 = t1;
t1 = tmp;
}
// Compare with current values
if (t0 > tNear) {
tNear = t0;
}
if (t1 < tFar) {
tFar = t1;
}
// Check if ray misses entirely
if (tNear > tFar) {
return false;
}
if (tFar < 0) {
return false;
}
}
// Box definitely intersected
if (tNear > 0) {
