Schneider P., Eberly D.H. Geometric Tools for Computer Graphics
Подождите немного. Документ загружается.

634 Chapter 11 Intersection in 3D
tIntersect = tNear;
} else {
tIntersect = tFar;
}
return true;
}
11.12.4 Plane and Axis-Aligned Bounding Box
This section discusses the problem of intersecting a plane and an axis-aligned bound-
ing box. Unlike other intersection solutions we present, here we only detect whether
an intersection has occurred. The reason is that AABBs are not geometric primitives
in themselves, but rather are used to bound other primitives, generally in the context
of quick rejection algorithms (as for rendering or collision detection): if no plane-
AABB intersection exists, we needn’t check the bounded primitive(s); if a plane-
AABB intersection does exist, then we go on to find the true intersection between
the bounded primitive(s) and the plane.
The simplest approach to the plane-AABB intersection problem is to simply note
that an intersection exists if and only if there are corners of the AABB on either side
of the plane. Note, however, that we may have to check every corner; this inefficiency
may not seem so bad (checking which side of a plane a point is on is not extremely
expensive), unless you consider that in a typical usage a huge number of AABBs may
need to be checked for intersection.
In this problem, we define the AABB in the usual fashion, by a pair of points
P
min
=
[
x
min
y
min
z
min
]
P
max
=
[
x
max
y
max
z
max
]
and a plane in the coordinate-free version of the implicit form (see Section 9.2.1):
n · (P − P
0
) = 0.
Figure 11.67 shows the intersection of a plane and an AABB.
M
¨
oller and Haines (1999) make the following observation: if we consider the
diagonals of the AABB, the one aligned most closely with the plane normal will have
at its end points the only pair of points that need be tested. This is a bit easier to see in
a 2D version, as shown in Figure 11.68. Another optimization can be employed: once
the most-aligned diagonal is found, if the minimal point is on the positive side of the
plane, we can immediately conclude that the plane doesn’t intersect the box because
the maximal point will be on the positive side of the plane as well.
11.12 Miscellaneous 635
The pseudocode is
boolean PlaneIntersectAABB(Plane plane, AABB box)
{
// Find points at end of diagonal
// nearest plane normal
foreach (dir in (x, y, z)) {
if (plane.normal[dir] >= 0) {
dMin[dir] = box.min[dir];
dMax[dir] = box.max[dir];
} else {
dMin[dir] = box.max[dir];
dMax[dir] = box.min[dir];
}
}
// Check if minimal point on diagonal
// is on positive side of plane
if (Dot(plane.normal, dMin) + plane.d) >= 0) {
return false;
} else {
return true;
}
}
11.12.5 Plane and Oriented Bounding Box
Here, we consider the problem of finding whether or not a plane and an oriented
bounding box intersect, again stopping short of computing the actual intersection
for the reasons previously given. Figure 11.69 illustrates this problem.
M
¨
oller and Haines (1999) suggest that because an OBB is simply an AABB in
a transformed frame, we can simply transform the plane normal ˆn into the frame
defined by the OBB’s center and basis vectors, and apply the same algorithm we used
on the AABB. The transformed normal vector is
ˆn
=
[
ˆu ·ˆn ˆv ·ˆn ˆw ·ˆn
]
This transformed normal can then be used in the plane-AABB intersection algorithm,
which otherwise remains as is. However, recall that the AABB is defined by a pair of
points, while the OBB is defined by a position, orientation frame, and half-width,
half-height, and half-depth. Thus, to use the AABB algorithm, we’d have to find the
minimal and maximal points of the OBB, in the frame defined by the OBB center and
basis vectors, and then apply the AABB algorithm.
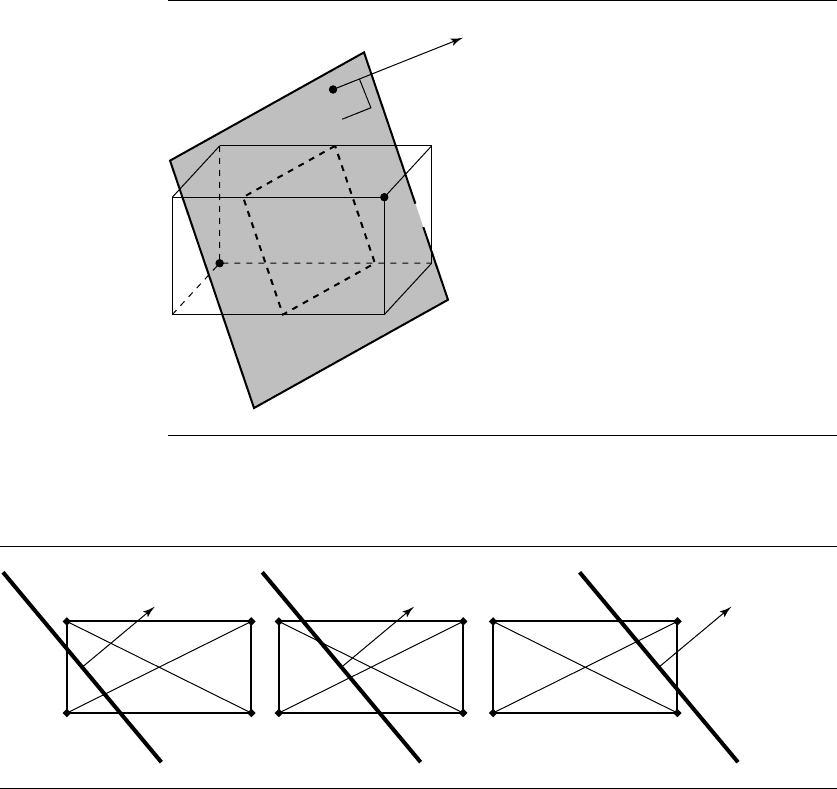
636 Chapter 11 Intersection in 3D
P
0
P
min
P
max
ˆn
Figure 11.67
Intersection of a plane and an axis-aligned bounding box.
Figure 11.68 We only need to check the corners at the end of the diagonal most closely aligned with
the normal to the plane.
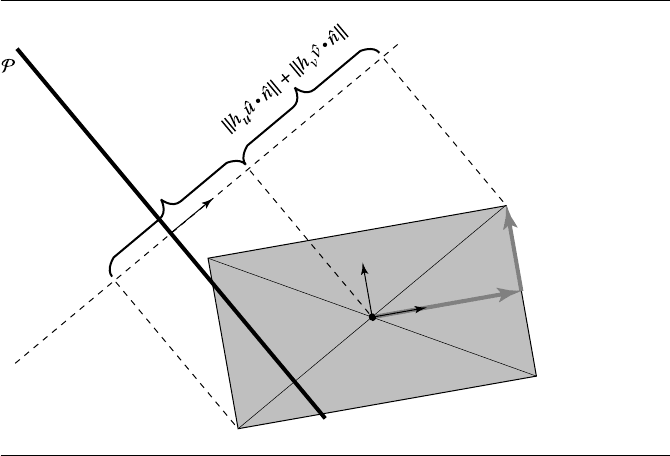
Another method cited by M
¨
oller and Haines (1999) may be preferable. We project
the diagonals of the OBB onto the plane normal, and then if the plane and either
of the projected diagonals intersect, then the box and plane intersect. The trick em-
ployed is to not implement this literally, as this would not necessarily be as efficient as
possible. Rather, consider Figure 11.70: We can’t simply project the scaled basis vec-
tors onto the plane normal; instead, we take the projected length of each scaled basis
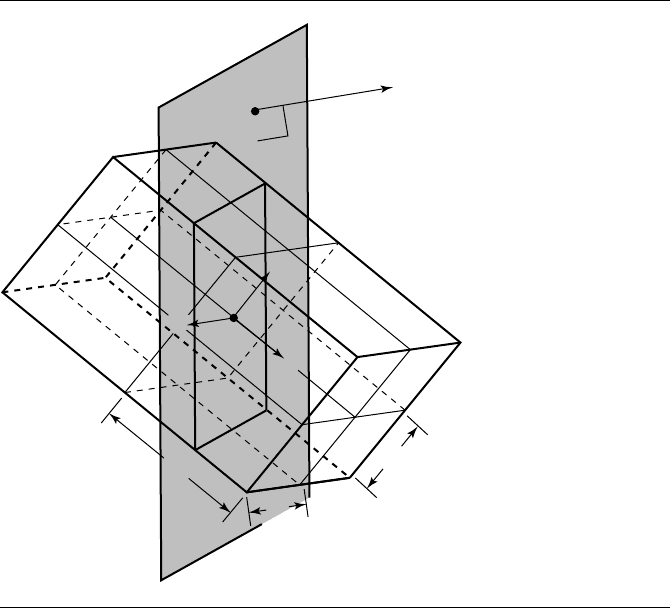
11.12 Miscellaneous 637
P
0
h
u
h
v
h
w
u
v
w
C
ˆn
Figure 11.69 The intersection of a plane and an oriented bounding box.
vector, and sum them. This gives us the half-length of the longest projected diagonal:
d =h
u
ˆu ·ˆn+h
v
ˆv ·ˆn
Clearly, if the (unsigned) distance between C and the plane P is less than d, then
the box and the plane do indeed intersect, and they do not otherwise. Of course, the
comparison can be done with the squares of these values, saving a square root in the
calculations.
11.12.6 Axis-Aligned Bounding Boxes
The intersection of two axis-aligned bounding boxes is made relatively simple by the
fact that the faces are perpendicular to their frame’s basis vectors. Figure 11.71 shows
638 Chapter 11 Intersection in 3D
h
v
v
C
ˆ
ˆ
n
h
u
û
ˆ
v
û
Figure 11.70 Projecting the diagonal of an OBB onto the plane normal.
two intersecting AABBs. The trick here is to create a test for nonoverlapping AABBs
for each basis vector direction: if the AABBs fail to overlap in any direction, then
they must not intersect at all; if the AABBs overlap in all directions, then they must
intersect.
The pseudocode is
boolean AABBIntersectAABB(AABB a, AABB b)
{
// Check if AABBs fail to overlap in any direction
foreach (dir in {x, y, z}) {
if (a.min[dir] > b.max[dir] || b.min[dir] > a.max[dir]) {
return false;
}
}
// AABBs overlapped in all directions, so they intersect
return true;
}
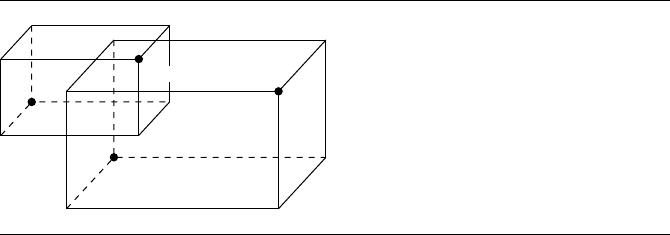
11.12 Miscellaneous 639
P
min
P
max
Q
min
Q
max
Figure 11.71 Intersection of two axis-aligned bounding boxes.
11.12.7 Oriented Bounding Boxes
In this section we discuss the problem of detecting the intersection of oriented
bounding boxes. An OBB is defined in Section 11.12.3 by a centerpoint C, a right-
handed orthonormal basis {ˆu, ˆv, ˆw}, and half-lengths {h
ˆu
, h
ˆv
, h
ˆw
}. Because OBBs are
used to bound other primitives for the purpose of speeding up intersection, picking,
or (perhaps) rendering operations by culling out cases that definitely do not intersect,
we only are concerned with finding out if there is an intersection; if the OBB’s do in-
tersect, then the primitives they bound may or may not, and we must then perform
the object-specific tests on the bounded primitives.
The algorithm we present is due to Gottschalk, Lin, and Manocha (1996). The
motivation is this: The naive approach would be to simply test every edge of each
OBB against every face of the other, yielding 144 edge-face tests. Much more efficient
is the use of the separating axis test, which is based on the following theorem: any two
nonoverlapping polytopes can always be separated by a plane that is either parallel to
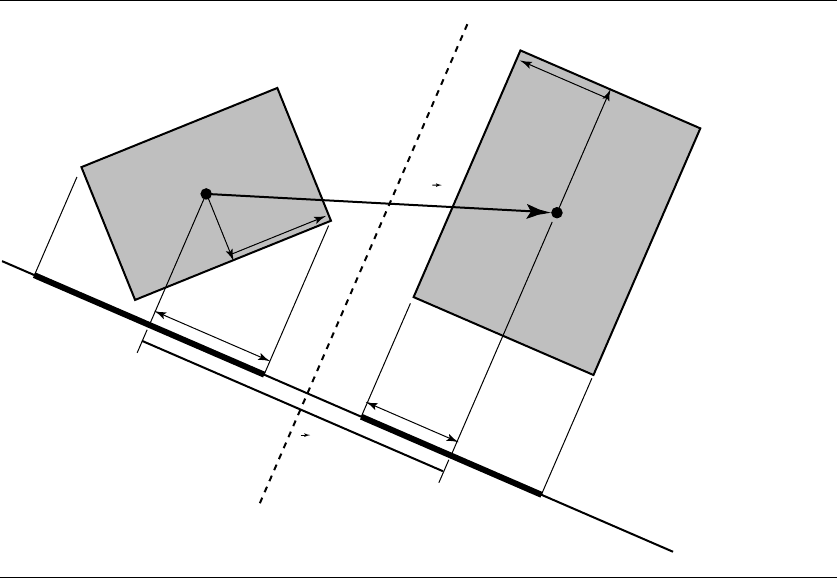
a face of one of the polytopes or parallel to an edge of each. An illustration in 2D
will help make this more clear; see Figure 11.72. The plane (line in 2D) that separates
OBBs A and B is shown as a dotted line.
Each OBB has three face orientations and three edge directions. This gives us a
total of 15 axes to test—3 faces from each of two boxes and 9 combinations of edges.
If the OBBs don’t overlap, then there will be at least one separating axis; if the OBBs
do overlap, there will be none. Note that in general, if the OBBs are nonoverlapping,
then a separating axis will be found (on average) in fewer than 15 tests.
The basic test is as follows:
1. Choose an axis to test.
2. Project the centers of the OBBs onto the axis.
3. Compute the radii of the intervals r
A
and r
B
.
640 Chapter 11 Intersection in 3D
C
B
C
A
t
r
B
h
A,u
û
A
h
B,u
û
B
r
A
t • l
ˆ
l
ˆ
h
B,v
v
B
ˆ
h
A,v
v
A
ˆ
Figure 11.72 2D schematic for OBB intersection detection. After Gottschalk, Lin, and Manocha
(1996).
4. If the sum of the radii is less than the distance between the projection of OBB
centers C
A
and C
B
onto the chosen axis, then the intervals are nonoverlapping,
and the OBBs are as well.
The “trick” employed here for efficiency is to treat the center C
A
and orientation
vectors {ˆu
A
, ˆv
A
, ˆw
A
} as an origin and basis, respectively, for a (coordinate) frame.
Then, OBB B is considered in terms of a rotation and translation T relative to A;in
this way, the three columns of R are just the three vectors {ˆu
B
, ˆv
B
, ˆw
B
}.
The radii r
A
and r
B
of the projection can be obtained by scaling the bases of the
OBBs by their associated half-dimensions, projecting each onto the separating axis,
and summing:
r
A
=
i∈{u,v,w}
h
A,i
|a
A,i
·
ˆ
l|
11.12 Miscellaneous 641
where a
A,i
is the axis of A associated with ˆu, ˆv,or ˆw, respectively, and similarly for
r
B
.
If we let
t = C
B
− C
A
, then the intervals are nonoverlapping if
|
t ·
ˆ
l| >r
A
+ r
B
There are three basic cases to consider: when the axis to test is parallel to an edge
of A, parallel to an edge of B, or a pairwise combination of an edge from each of A
and B.
ˆ
l Is Parallel to an Edge of A
This is the simplest case. Because we’re using C
A
and {ˆu
A
, ˆv
A
, ˆw
A
, } as a basis, the
axes {ˆa
A,u
, ˆa
A,v
, ˆa
A,w
} are [
100
], [
010
], and [
001
], respectively.
For example, if we’re testing the axis parallel to ˆu
A
, the projected distance between
C
A
and C
B
is
|
t ·
ˆ
l|=|
t · a
A,u
|
=|x
t
|
The projected radius of A is
r
A
=
i∈{u,v,w}
h
A,i
|a
A,i
·
ˆ
l|
but since
ˆ
l =ˆu
A
we have
r
A
=
i∈{u,v,w}
h
A,i
|a
A,i
· a
A,u
|
= h
A,u
The projected radius of B is
r
B
=
i∈{u,v,w}
h
B,i
|a
B,i
·
ˆ
l|
but since
ˆ
l =ˆu
a
642 Chapter 11 Intersection in 3D
we have
r
B
=
i∈{u,v,w}
h
B,i
|a
B,i
· a
u
|
= h
B,u
|R
00
|+h
B,v
|R
01
|+h
B,w
|R
02
|
The cases where
ˆ
l =ˆv
A
and
ˆ
l =ˆw
A
are analogous.
ˆ
l Is Parallel to an Edge of B
This is almost as simple as the case where
ˆ
l is parallel to an edge of A. For example, if
we’re testing the axis parallel to ˆu
B
, the projected distance between C
A
and C
B
is
|
t ·
ˆ
l|=|
t · a
B,u
|
=|t
x
R
00
+ t
y
R
10
+ t
z
R
20
|
The projected radius of A is
r
A
=
i∈{u,v,w}
h
A,i
|a
B,i
·
ˆ
l|
but since
ˆ
l =ˆu
B
we have
r
A
=
i∈{u,v,w}
h
A,i
|a
A,i
· a
B,u
|
= h
A,u
|R
00
|+h
A,v
|R
10
|+h
A,w
|R
20
|
The projected radius of B is
r
B
=
i∈{u,v,w}
h
B,i
|a
B,i
·
ˆ
l|
but since
ˆ
l =ˆu
a
11.12 Miscellaneous 643
we have
r
B
=
i∈{u,v,w}
h
B,i
|a
B,i
· a
u
|
= h
B,u
The cases where
ˆ
l =ˆv
B
and
ˆ
l =ˆw
B
are analogous.
ˆ
l Is a Combination of Edges from A and B
For testing axes that are combinations of edges from both OBBs, we use a vector that
is the cross product of basis vectors of A and B.
For example, if we’re testing the axis parallel to ˆu
A
׈v
B
, the projected distance
between C
A
and C
B
is
|
t ·
ˆ
l =|
t · (a
A,u
× a
B,v
)|
=|
t ·
[
0, −a
B,v,z
, a
B,v,y
]
|
=|t
z
R
11
− t
y
R
21
|
The projected radius of A is
r
A
=
i∈{u,v,w}
h
A,i
|a
A,i
·
ˆ
l|
but since
ˆ
l =(a
A,u
× a
B,v
)
we have
r
A
=
i∈{u,v,w}
h
A,i
|a
A,i
· (a
A,u
× a
B,v
)|
=
i∈{u,v,w}
h
A,i
|a
B,v
· (a
A,u
× a
A,i
)|
= h
A,v
|R
21
|+h
A,w
|R
11
|
The projected radius of B is
