Schneider P., Eberly D.H. Geometric Tools for Computer Graphics
Подождите немного. Документ загружается.

644 Chapter 11 Intersection in 3D
r
B
=
i∈{u,v,w}
h
B,i
|a
B,i
·
ˆ
l|
but since
ˆ
l =(a
A,u
× a
B,v
)
we have
r
B
=
i∈{u,v,w}
h
B,i
|a
B,i
· (a
A,u
× a
B,v
)|
=
i∈{u,v,w}
h
B,i
|a
A,v
· (a
B,i
× a
B,v
)|
= h
B,u
|R
02
|+h
B,w
|R
00
|
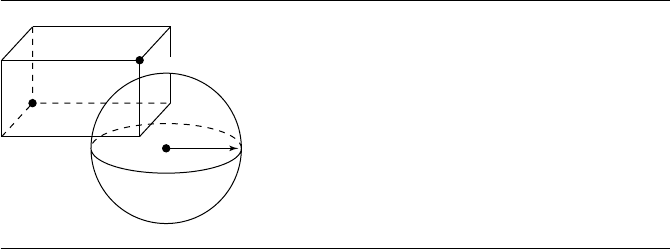
11.12.8 Sphere and Axis-Aligned Bounding Box
In this section we address the problem of the intersection of an axis-aligned bounding
box and a sphere. The AABB is defined by the two opposing corners with the least and
greatest component values
P
min
=
[
x
min
y
min
z
min
]
P
max
=
[
x
max
y
max
z
max
]
while the sphere is simply defined by its center C and radius r, as shown in Fig-
ure 11.73.
P
min
P
max
C
r
Figure 11.73
Intersection of an axis-aligned bounding box and a sphere.
11.12 Miscellaneous 645
An algorithm due to Arvo (1990) describes a rather clever way of determining
whether or not a sphere intersects an AABB. The basic idea is to find the point on (or
in) the AABB that is closest to the center of the sphere: if its squared distance is less
than the sphere’s squared radius, they intersect; otherwise, they do not. The clever
aspect is the efficient way in which Arvo found to find this closest point. The closest
point Q on (or in) the AABB minimizes the squared-distance function
dist
2
(Q) = (C
x
− Q
x
)
2
+ (C
y
− Q
y
)
2
+ (C
z
− Q
z
)
2
subject to
P
min,x
≤ Q
x
≤ Q
x
P
min,y
≤ Q
y
≤ Q
y
P
min,z
≤ Q
z
≤ Q
z
Arvo notes that we can find the minimum-distance point’s components indepen-
dently, which then can be combined to find the point itself.
The pseudocode is
boolean AABBIntersectSphere(AABB box, Sphere sphere)
{
// Initial distance is 0
float distSquared = 0;
// Compute distance in each direction,
// summing as we go.
foreach (dir in {x, y, z}) {
if (sphere.center[dir] < box.min[dir]) {
distSquared += Square((sphere.c[dir] - box.min[dir]));
} else if (sphere.center[dir] > box.max[dir]) {
distSquared += Square((sphere.c[dir] - box.max[dir]));
}
}
// Compare distance to radius squared
if (distSquared <= sphere.radius * sphere.radius) {
return true;
} else {
return false;
}
}
646 Chapter 11 Intersection in 3D
Arvo also provides a version that handles “hollow” primitives, in which complete
containment of one within the other means “no intersection,” and a version that
generalizes the above algorithm to ellipsoids (however, it should be noted that this
only works for ellipsoids whose axes are parallel to its defining frame’s basis vectors).
11.12.9 Cylinders
This section shows how to determine if two bounded cylinders intersect. The algo-
rithm uses the method of separating axes as discussed in Section 11.11, although the
construction is more complicated than what we encounter when separating convex
polyhedra since the bounded cylinders are not polyhedra. The resulting algorithm is
a fairly expensive one if you plan on using cylinders for bounding volumes in a real-
time graphics engine. A better alternative to a cylinder is a capsule, the set of points
a specified distance from a line segment. Two capsules intersect if and only if the dis-
tance between capsule line segments is smaller or equal to the sum of the capsule
radii, a much cheaper test to perform.
In addition to using the method of separating axes that relies on projecting onto
lines, the algorithm also requires separation by projection onto planes. The concept
is similar to separating axes. If there exists a plane for which the regions of projection
of the two convex objects onto that plane do not intersect, then the objects do not
intersect. Just as with lines, it is sufficient to consider planes that contain the origin.
Given a plane containing the origin and with unit-length normal ˆn, the projection of
aconvexsetC onto the line is the set of points
R ={Y : Y =X − ( ˆn · X)ˆn = (I −ˆn ˆn
T
)X, X ∈C}
where I is the 3 × 3 identity matrix. The projection set is itself a convex set. Two
convex sets C
0
and C
1
are separated if there exists a normal ˆn such that the projection
sets R
0
and R
1
do not intersect, R
0
∩R
1
=∅. The determination of this condition can
involve one of many geometric methods, for example, by showing that the distance
between the two sets is positive. It might be possible to analyze the projections in
native 2D and attempt to find a separating line in 2D, but such a construction should
work as well in 3D.
Representation of a Cylinder
A cylinder has a centerpoint C, unit-length axis direction ˆw,radiusr, and height h.
The end disks of the cylinder are located at C ± (h/2) ˆw.Let ˆu and ˆv be any unit-
length vectors so that {ˆu, ˆv, ˆw} is a right-handed set of orthonormal vectors. That
is, the vectors are unit length, mutually orthogonal, and ˆw =ˆu ׈v. Points on the
cylinder surface are parameterized by
11.12 Miscellaneous 647
X(θ, t)= C + (r cos θ)ˆu + (r sin θ)ˆv +t ˆw, θ ∈ [0, 2π), |t|≤h/2
The end disks are parameterized by
X(θ, ρ) = C +(ρ cos θ)ˆu + (ρ sin θ)ˆv ±(h/2) ˆw, θ ∈ [0, 2π), ρ ∈ [0, r]
The projections of a cylinder onto a line or plane are determined solely by the cylinder
wall, not the end disks, so the second parameterization is not relevant for intersection
testing.
The choice of ˆu and ˆv is arbitrary. Intersection queries between cylinders should
be independent of this choice, but some of the algorithms are better handled if
a choice is made. A quadratic equation that represents the cylinder wall is (X −
C)
T
(I −ˆw ˆw
T
)(X − C) = r
2
. The boundedness of the cylinder is specified by |ˆw ·
(X − C)|≤h/2. This representation is dependent only on C, ˆw, r, and h.
Projection of a Cylinder onto a Line
Let the line be s
d,where
d is a nonzero vector. The projection of a cylinder point
onto the line is
λ(θ, t) =
d · X(θ, t) =
d · C + (r cos θ)
d ·ˆu + (r sin θ)
d ·ˆv + t
d ·ˆw.
The interval of projection has end points determined by the extreme values of this
expression. The maximum value occurs when all three terms involving the parame-
ters are made as large as possible. The t-term has a maximum of (h/2)|
d ·ˆw|.The
θ-terms, not including the radius, can be viewed as a dot product (cos θ , sin θ) · (
d ·
ˆu,
d ·ˆv). This is maximum when (cos θ, sin θ)is in the same direction as (
d ·ˆu,
d ·ˆv).
Therefore,
(cos θ, sin θ) =
(
d ·ˆu,
d ·ˆv)
(
d ·ˆu)
2
+ (
d ·ˆv)
2
and the maximum projection value is
λ
max
=
d · C + r
d
2
− (
d ·ˆw)
2
+ (h/2)|
d ·ˆw|
where we have used the fact that
d = (
d ·ˆu) ˆu + (
d ·ˆv)ˆv + (
d ·ˆw) ˆw, which implies
(
d ·ˆu)
2
+ (
d ·ˆv)
2
+ (
d ·ˆw)
2
=
d
2
. The minimum projection value is similarly
derived:
λ
min
=
d · C − r
d
2
− (
d ·ˆw)
2
− (h/2)|
d ·ˆw|
648 Chapter 11 Intersection in 3D
Projection of a Cylinder onto a Plane
Let the plane be ˆn · X = 0, where ˆn is a unit-length normal. The projection of a
cylinder onto a plane has one of three geometric configurations:
1. A disk when ˆw is parallel to ˆn
2. A rectangle when ˆw is perpendicular to ˆn
3. A rectangle with hemielliptical caps
The projection matrix is P = I −ˆn ˆn
T
. In the first case, the center of the disk is
PC and the radius is r. In the second case, the rectangle has center PC and has unit-
length axis directions ˆw and ˆw ׈n. The four corners of the rectangle are PC ±r ˆw ×
ˆn ± (h/2) ˆw.
The third case is only slightly more complicated. The centerpoint of the projec-
tion region is PC. The axis of the projection region has non-unit-length direction
P ˆw. An axis of the cylinder that is in the plane and perpendicular to ˆn has direction
ˆu = (P ˆw) ׈n/(P ˆw) ׈n. The four points on the cylinder that map to the four
corners of the rectangular portion of the projection are C ± r ˆu ± (h/2) ˆw. The four
corners are PC ± r ˆu ± (h/2)P ˆw.
Let ˆv =ˆw ׈u. The end circles of the cylinder are X(θ) = C ± r((cos θ)ˆu +
(sin θ)ˆv) ±(h/2) ˆw.LetY =P(X −C ±(h/2) ˆw); then Y =r((cos θ)ˆu +(sin θ)P ˆv).
Therefore, ˆu · Y = r cos θ and Pˆv · Y =P ˆv
2
r sin θ . Combining these yields
1 =
1
r
2
( ˆu · Y)
2
+
1
P ˆv
4
(P ˆv ·Y)
2
=
1
r
2
Y
T
ˆu ˆu
T
+
1
P ˆv
2
P ˆv
P ˆv
P ˆv
P ˆv
T
Y
= (P(X − C ±(h/2) ˆw))
T
1
r
2
ˆu ˆu
T
+
1
r
2
P ˆv
2
P ˆv
P ˆv
P ˆv
P ˆv
T
(P(X − C ± (h/2) ˆw))
This is the equation for two ellipses with centers at P(C ± (h/2) ˆw),axesˆu and
P ˆv/P ˆv, and axis half-lengths r and rP ˆv.
Separating Line Tests for Two Cylinders
Given two cylinders with centers C
i
, axis directions ˆw
i
, radii r
i
, and heights h
i
, for
i = 0, 1, the cylinders are separated if there exists a nonzero direction
d such that
either
d · C
0
− r
0
d
2
− (
d ·ˆw
0
)
2
− (h
0
/2)|
d ·ˆw
0
| >
d · C
1
+ r
1
d
2
− (
d ·ˆw
1
)
2
+ (h
1
/2)|
d ·ˆw
1
|

11.12 Miscellaneous 649
or
d · C
0
+ r
0
d
2
− (
d ·ˆw
0
)
2
+ (h
0
/2)|
d ·ˆw
0
| <
d · C
1
− r
1
d
2
− (
d ·ˆw
1
)
2
− (h
1
/2)|
d ·ˆw
1
|
Defining
> = C
1
− C
0
, these tests can be rewritten as a single expression, f(
d) < 0,
where
f(
d) =r
0
P
0
d+r
1
P
1
d+(h
0
/2)|
d ·ˆw
0
|+(h
1
/2)|
d ·ˆw
1
|−|
d ·
>|
and where P
i
= I −ˆw
i
ˆw
T
i
for i = 0, 1.
If
> = 0, then f ≥ 0. This is geometrically obvious since two cylinders with the
same center already intersect. The remainder of the discussion assumes
> =
0. If
d is
perpendicular to
>, then f(
d) ≥0. This shows that any line perpendicular to the line
containing the two cylinder centers can never be a separating axis. This is also clear
geometrically. The line of sight C
0
+ s
> intersects both cylinders at their centers.
If you project the two cylinders onto the plane
> · (X − C
0
) = 0, both regions of
projection overlap. No matter which line you choose containing C
0
in this plane, the
line intersects both projection regions.
If
d is a separating direction, then f(
d) < 0. Observe that f(t
d) =|t|f(
d),so
f(t
d)< 0 for any t. This is consistent with the geometry of the problem. Any nonzero
multiple of a separating direction must itself be a separating direction. This allows
us to restrict our attention to the unit sphere, |
d|=1. Function f is continuous on
the unit sphere, a compact set, so f must attain its minimum at some point on
the sphere. This is a minimization problem in two dimensions, but the spherical
geometry complicates the analysis somewhat. Different restrictions on the set of
potential separating directions can be made that yield minimization problems in a
line or a plane rather than on a sphere.
The analysis of f involves computing its derivatives,
∇(f ), and determining its
critical points. These are points for which
∇(f ) is zero or undefined. The latter
category is easy to specify. The gradient is undefined when any of the terms inside
the five absolute value signs is zero. Thus,
∇(f ) is undefined at ˆw
0
, ˆw
1
, at vectors that
are perpendicular to ˆw
0
, at vectors that are perpendicular to ˆw
1
, and at vectors that
are perpendicular to
>. We already argued that f ≥ 0 for vectors perpendicular to
>,
so we can ignore this case.
Tests at ˆw
0
, ˆw
1
, and ˆw
0
׈w
1
The cylinder axis directions themselves can be tested first for separation. The test
function values are
f(ˆw
0
) = r
1
ˆw
0
׈w
1
+(h
0
/2) + (h
1
/2)|ˆw
0
·ˆw
1
|−|ˆw
0
·
>|
650 Chapter 11 Intersection in 3D
and
f(ˆw
1
) = r
0
ˆw
0
׈w
1
+(h
0
/2)|ˆw
0
·ˆw
1
|+(h
1
/2) −|ˆw
1
·
>|
If either function value is negative, the cylinders are separated. The square roots can
be avoided. For example, the test f(ˆw
0
)<0 is equivalent to
r
1
ˆw
0
׈w
1
< |ˆw
0
·
>|−h
0
/2 −(h
1
/2)|ˆw
0
·ˆw
1
|=: ρ
The right-hand side is evaluated. If ρ ≤ 0, then the inequality cannot be true since
ˆw
0
׈w
1
=
0 and the left-hand side is positive. Otherwise, ρ>0 and it is now enough
to test r
1
ˆw
0
׈w
1
2
<ρ
2
. A similar construction applies to f(ˆw
1
)<0.
One last test that does not require many more operations and might lead to a
quick no-intersection test is
f(ˆw
0
׈w
1
) = (r
0
+ r
1
)ˆw
0
׈w
1
−|ˆw
0
׈w
1
·
>| < 0
or equivalently
(r
0
+ r
1
)
2
ˆw
0
׈w
1
2
< |ˆw
0
׈w
1
·
>|
2
assuming of course that ˆw
0
׈w
1
=
0. This vector is actually one for which the gradi-
ent of f is undefined.
If ˆw
0
and ˆw
1
are parallel, then ˆw
0
׈w
1
=
0 and |ˆw
0
·ˆw
1
|=1. The identity
(a ×
b) · (c ×
d) =(a ·c)(
b ·
d) −(a ·
d)(
b ·c)
can be used to show that ˆw
0
׈w
1
2
= 1 − ( ˆw
0
·ˆw
1
)
2
. The test function for ˆw
0
evaluates to
f(ˆw
0
) = (h
0
+ h
1
)/2 −|ˆw
0
·
>|
The two cylinders are separated if (h
0
+ h
1
)/2 < |ˆw
0
·
>|.Iff(ˆw
0
) ≥ 0, the two
cylinders are potentially separated by a direction that is perpendicular to ˆw
0
.Geo-
metrically it is enough to determine whether or not the circles of projection of the
cylinders onto the plane ˆw
0
· X =
0 intersect. These circles are disjoint if and only if
the length of the projection of
> onto that plane is larger than the sum of the radii of
the circles. The projection of
> is
> − ( ˆw
0
·
>) ˆw
0
, and its squared length is
> − ( ˆw
0
·
>) ˆw
0
2
=
>
2
− ( ˆw
0
·
>)
2
The sum of the radii of the circles is the sum of the radii of the cylinders, r
0
+ r
1
,so
the two cylinders are separated if
>
2
− ( ˆw
0
·
>)
2
>(r
0
+ r
1
)
2
.
For the remainder of this section we assume that ˆw
0
and ˆw
1
are not parallel.

11.12 Miscellaneous 651
Tests at Vectors Perpendicular to ˆw
0
or ˆw
1
Considering the domain of f to be the unit sphere, the set of vectors perpendicular
to ˆw
0
is a great circle on the sphere. The gradient of f is undefined on this great
circle. Define
d(θ) =(cos θ)ˆu
0
+(sin θ)v
0
and F(θ)= f(
d(θ)). If we can show that
F(θ)<0 for some θ ∈ [0, 2π), then the corresponding direction is a separating line
for the cylinders. However, F is a somewhat complicated function that does not lend
itself to a simple analysis. Since f(−
d) = f(
d), we may restrict our attention to only
half of the great circle. Rather than restricting f to a half circle, we can restrict it to a
tangent line
d(x) =x ˆu
0
+ˆv
0
and define F(x)= f(
d(x)),so
F(x)= r
0
x
2
+ 1 + r
1
(P
1
ˆu
0
)x +(P
1
ˆv
0
)+(h
1
/2)|( ˆw
1
·ˆu
0
)x
+ ( ˆw
1
·ˆv
0
)|−|(
·ˆu
0
)x +(
·ˆv
0
)|
= r
0
x
2
+ 1 + r
1
a
0
x +
b
0
+(h
1
/2)a
1
x +
b
1
−a
2
x +
b
2
This function is more readily analyzed by breaking it up into four cases by replac-
ing the last two absolute values with sign indicators,
G(x) = r
0
x
2
+ 1 + r
1
a
0
x +
b
0
+σ
1
(h
1
/2)(a
1
x +
b
1
) − σ
2
(a
2
x +
b
2
)
with |σ
1
|=|σ
2
|=1. The minimum of G is calculated for each choice of (σ
1
, σ
2
) by
computing G
(x) and determining where it is zero or undefined. Any critical point x
must first be tested to see if it is consistent with the choice of signs. That is, a critical
point must be tested to make sure σ
1
(a
1
x +b
1
) ≥ 0 and σ
2
(a
2
x +b
2
) ≥ 0. If so, then
G(x) is evaluated and compared to zero. The derivative is
G
(x) = r
0
x
√
x
2
+ 1
+ r
1
a
0
·
a
0
x +
b
0
a
0
x +
b
0
+ (σ
1
h
1
/2)a
1
− σ
2
b
2
The derivative is undefined when a
0
x +
b
0
=0, but this case is actually gen-
erated when the original direction is parallel to ˆw
0
׈w
1
, discussed earlier. To al-
gebraically solve G
(x) = 0, a few squaring operations can be applied. Note that
G
(x) = 0 is of the form
L
0
Q
0
+ L
1
Q
1
= c
Q
0
Q
1
where L
i
are linear in x, Q
i
are quadratic in x, and c is a constant. Squaring and
rearranging terms yields
2L
0
L
1
Q
0
Q
1
= c
2
Q
0
Q
1
− L
2
0
Q
0
− L
2
1
Q
1
652 Chapter 11 Intersection in 3D
Squaring again and rearranging terms yields
4L
2
0
L
2
1
Q
0
Q
1
− (c
2
Q
0
Q
1
− L
2
0
Q
0
− L
2
1
Q
1
)
2
= 0
The left-hand side is a polynomial in x of degree 8. The roots can be computed by
numerical methods, tested for validity as shown earlier, and then G can be tested for
negativity.
Yet one more alternative is to notice that attempting to locate a separating direc-
tion that is perpendicular to ˆw
0
is equivalent to projecting the two cylinders onto the
plane ˆw
0
· X = 0 and determining if the projections are disjoint. The first cylinder
projects to a disk. The second cylinder projects to a disk, a rectangle, or a rectangle
with hemielliptical caps depending on the relationship of ˆw
1
to ˆw
0
. Separation can
be determined by showing that (1) the projection of C
0
is not inside the projection
of the second cylinder and (2) the distance from C
0
to the projection of the second
cylinder is larger than r
0
. If the second projection is a disk, the distance is just the
length of the projection of
. If the second projection is a rectangle, then the prob-
lem amounts to computing the distance between a point and a rectangle in the plane.
This test is an inexpensive one. If the second projection is a rectangle with hemiel-
liptical caps, then the problem amounts to computing the minimum of the distances
between a point and a rectangle and two ellipses, then comparing it to r
0
. Calculat-
ing the distance between a point and an ellipse in the plane requires finding roots of a
polynomial of degree 4. This alternative trades off, in the worst case, finding the roots
to a polynomial of degree 8 for finding the roots of two polynomials of degree 4.
Tests for Directions at Which
∇(f ) =
0
The symmetry f(−
d) = f(
d) implies that we only need to analyze f onahemi-
sphere; the other hemisphere values are determined automatically. Since f ≥ 0on
the great circle of vectors that are perpendicular to
, we can restrict our attention to
the hemisphere whose pole is ˆw =
/
. Rather than project onto the hemisphere,
we can project onto the tangent plane at the pole. The mapping is
d =x ˆu +y ˆv +ˆw,
where ˆu, ˆv, and ˆw form a right-handed orthonormal set. Defining the rotation matrix
R = [ˆu|ˆv|ˆw]and
ξ = (x, y,1), the function f reduces to
F(x, y) = r
0
P
0
R
ξ+r
1
P
1
R
ξ+(h
0
/2)|ˆw
0
· R
ξ|+(h
1
/2)|ˆw
1
· R
ξ|−
for (x, y) ∈ R
2
. To determine if F(x, y) < 0 for some (x, y), it is enough to show
that the minimum of F is negative. The point at which the minimum is attained
occurs when the gradient of F is zero or undefined.
∇(F ) is undefined at points for
which any of the first four absolute value terms is zero. In terms of points
d on the
unit sphere, the first term is zero at ˆw
0
, the second term is zero at ˆw
1
, the third term
is zero at any vector perpendicular to ˆw
0
, and the fourth term is zero at any vector
11.12 Miscellaneous 653
perpendicular to ˆw
1
. After all such points have been tested only to find that F ≥ 0,
the next phase of the separation test is to compute solutions to
∇(F ) =
0 and test if
any of those force F<0.
If
d is a separating direction, then f(
d) < 0. Observe that f(t
d) =|t|f(
d),so
f(t
d)< 0 for any t. This is consistent with the geometry of the problem. Any nonzero
multiple of a separating direction must itself be a separating direction. This allows
us to restrict our attention to the unit sphere, |
d|=1. Function f is continuous on
the unit sphere, a compact set, so f must attain its minimum at some point on the
sphere. This is a minimization problem in two dimensions, but the spherical geome-
try complicates the analysis somewhat. A different restriction on the set of potential
separating directions can be made that yields a two-dimensional minimization in the
plane rather than a two-dimensional minimization on a sphere.
First, some notation. The function f(
d) can be written as
f(
d) =r
0
A
T
0
d+r
1
A
T
1
d+(h
0
/2)|
d ·ˆw
0
|+(h
1
/2)|
d ·ˆw
1
|−|
d ·
|
where the matrices A
i
=[ˆu
i
|v
i
]are 3× 2. Observe that A
T
i
A
i
=I
2
, the 2 ×2 identity,
and A
i
A
T
i
= I
3
−ˆw
i
ˆw
T
i
,whereI
3
is the 3 × 3 identity matrix.
The symmetry f(−
d) = f(
d) implies that we only need to analyze f onahemi-
sphere; the other hemisphere values are determined automatically. The complicating
factor in directly analyzing f turns out to be the presence of the absolute value terms
|
d ·ˆw
0
|, |
d ·ˆw
1
|, and |
d ·
|. Instead we will look at functions where the absolute
values are removed. To illustrate, consider
g
0
(
d) =r
0
A
T
0
d+r
1
A
T
1
d−
d ·
φ
where
φ =
− (h
0
/2) ˆw
0
− (h
1
/2) ˆw
1
. If the analysis of g
0
produces a direction
d
for which g
0
(
d) < 0 and if
d ·ˆw
0
≥ 0,
d ·ˆw
1
≥ 0, and
d ·
≥ 0, then f(
d) < 0
and we have a separating direction. However, the inequality constraints might not
be satisfied, even when g
0
(
d) < 0, in which case
d is rejected as a candidate for
separation. The companion function is
g
1
(
d) =r
0
A
T
0
d+r
1
A
T
1
d+
d ·
φ
If the analysis of g
1
produces a direction
d for which g
1
(
d) < 0 and if
d ·ˆw
0
≤ 0,
d ·ˆw
1
≤0, and
d ·
≤0, then f(
d) < 0 and we have a separating direction. However,
the inequality constraints might not be satisfied, even when g
1
(
d) < 0, in which case
d is rejected as a candidate for separation. There are four such pairs of functions to
consider, exhausting all eight sign possibilities on the three absolute value terms.
Let us now analyze g
0
(
d).If
φ =
0, then clearly g
0
(
d) ≥ 0 for all directions, so no
separation can occur. For the remainder of the argument, assume
φ =
0. Any direc-
tion
d for which
d ·
φ ≤0 cannot be a separating direction. This allows us to restrict
