Schneider P., Eberly D.H. Geometric Tools for Computer Graphics
Подождите немного. Документ загружается.


654 Chapter 11 Intersection in 3D
our attention to a hemisphere of directions whose pole is ˆw =
φ/
φ.Moreover,we
can avoid working on the hemisphere by projecting those points radially outward
onto the tangent plane at the pole. That is, we need only analyze g
0
for directions
d = x ˆu + y ˆv +ˆw,where{ˆu, ˆv, ˆw} forms a right-handed orthonormal set of vectors.
Defining the rotation matrix R =[ˆu|ˆv|ˆw] whose columns are the indicated vectors,
the restriction of g
0
to the plane is F(x, y) = g
0
(
d) = g
0
(R
ξ),where
ξ =(x, y,1),so
F(x, y) = r
0
A
T
0
R
ξ+r
1
A
T
1
R
ξ−
φ (11.43)
In order to determine if F(x, y) < 0 for some (x, y), we will determine the
minimum of F and test if it is negative. The minimum must occur at critical points,
those points where
∇F is zero or undefined. Any critical points that do not satisfy the
inequality constraints for g
0
are rejected since F can be viewed as the restriction of
g
0
to a convex subset of the plane defined by the inequality constraints. We only need
to compute the minimum of F on this convex subset, so critical points outside that
convex set are irrelevant. Analysis of the corresponding F(x, y) for the companion
function g
1
uses the projection
d = x ˆu + y ˆv −ˆw.
Analysis of F(x, y)
Using ∂R
ξ/∂x =ˆu and ∂R
ξ/∂y =ˆv, the partial derivatives of F are
∂F
∂x
=ˆu ·
r
0
A
0
A
T
0
R
ξ
A
T
0
R
ξ
+ r
1
A
1
A
T
1
R
ξ
A
T
1
R
ξ
and
∂F
∂y
=ˆv ·
r
0
A
0
A
T
0
R
ξ
A
T
0
R
ξ
+ r
1
A
1
A
T
1
R
ξ
A
T
1
R
ξ
If we define A = [ˆu|ˆv], the equation
∇F(x, y) = (0, 0) can be summarized by
A
T
r
0
A
0
A
T
0
R
ξ
A
T
0
R
ξ
+ r
1
A
1
A
T
1
R
ξ
A
T
1
R
ξ
=
0
Define the unit-length vectors ˆη
i
= A
T
i
R
ξ/A
T
i
R
ξ for i = 0, 1. Define the 2 × 2
matrices B
i
= A
T
A
i
. The system of equations to be solved is
r
0
B
0
ˆη
0
+ r
1
B
1
ˆη
1
=
0, ˆη
0
2
= 1, and ˆη
1
2
= 1 (11.44)
Given any solution ˆη
0
and ˆη
1
to these equations, it must be that ˆη
i
and A
T
i
R
ξ point
in the same direction. That is,
11.12 Miscellaneous 655
ˆη
⊥
0
·A
T
0
R
ξ =0, ˆη
⊥
1
·A
T
1
R
ξ =0, ˆη
0
·A
T
0
R
ξ>0, and ˆη
1
·A
T
1
R
ξ>0 (11.45)
where (a, b)
⊥
= (b, −a). Each pair (x, y) that satisfies these conditions is a critical
point for F(x, y) with
∇F(x, y) = (0, 0). The critical point can then be tested to see
if F(x, y) < 0, in which case the cylinders are separated.
The outline of the algorithm for the analysis of g0(
d(x, y)) = F(x, y) is
1. Using the notation R
i
=[ˆu
i
|v
i
|ˆw
i
]for i =0, 1, the various dot products of vectors
required in the algorithm need to be computed. The 18 values are represented
abstractly as G
0
= R
T
R
0
= [g
(0)
ij
] and G
1
= R
T
R
1
= [g
(1)
ij
].
2. Solve r
0
B
0
ˆη
0
+r
1
B
1
ˆη
1
=
0, ˆη
0
2
=1, and ˆη
1
2
=1 for ˆη
0
and ˆη
1
. Note that there
are multiple solution pairs, the obvious one being (−ˆη
0
, −ˆη
1
) whenever ( ˆη
0
, ˆη
1
)
is a solution. This negated pair leads to the same system of equations to extract
(x, y) in step 4, so it can be ignored.
3. For each solution pair ( ˆη
0
, ˆη
1
), solve ˆη
⊥
0
·A
T
0
R
ξ =0 and ˆη
⊥
1
·A
T
1
R
ξ =0 for
ξ. This
set of equations can also have multiple solutions.
4. For each solution
ξ, verify that ˆw
0
· R
ξ ≥ 0, ˆw
1
· R
ξ, ˆη
0
· A
T
0
R
ξ>0, and ˆη
1
·
A
T
1
R
ξ>0.
5. For each pair (x, y) from a valid
ξ in the last step, test if F(x, y) < 0. If so, then
d = R
ξ is a separating direction for the cylinders, and the algorithm terminates.
The algorithm for the analysis of g
1
(x ˆu + y v −ˆw) is identical in the first three
steps. The only difference in steps 4 and 5 is that
ξ =(x, y,1) for g
0
and
ξ =(x, y, −1)
for g
1
.
Solving for ˆη
i
Note that
B
i
=
ˆu ·ˆu
i
ˆu ·v
i
ˆv ·ˆu
i
ˆv ·v
i
so
det(B
i
) = ( ˆu ·ˆu
i
)( ˆv ·v
i
) − ( ˆu ·v
i
)( ˆv ·ˆu
i
) = ( ˆu ׈v) · ( ˆu
i
×v
i
) =ˆw ·ˆw
i
If det(B
0
) = 0 and det(B
1
) = 0, then ˆw must be perpendicular to both ˆw
0
and ˆw
1
.
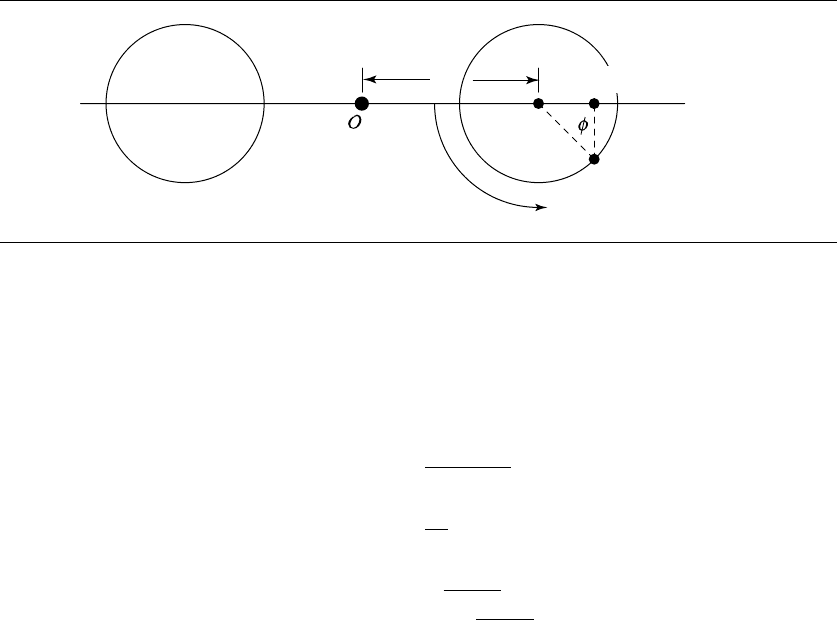
Since ˆw =
φ/
φ,
φ is perpendicular to both ˆw
0
and ˆw
1
. Observe that
φ = (C
1
−
(h
1
/2) ˆw
1
) −(C
0
+(h
0
/2) ˆw
0
), a difference of two cylinder end points, one from each
cylinder. The line segment connecting the two end points is therefore perpendicular

656 Chapter 11 Intersection in 3D
to each cylinder. Draw yourself a picture to see that intersection/separation is deter-
mined solely by testing the direction
d =ˆw. Note that this direction does satisfy the
inequality constraints since ˆw ·ˆw
0
= 0, ˆw ·ˆw
1
= 0, and ˆw ·
=ˆw ·
φ =
φ > 0.
The two cylinders are separated if and only if
φ
2
>(r
0
+ r
1
)
2
.
If det(B
0
) = 0 and det(B
1
) = 0, then the columns of B
1
are linearly dependent.
Moreover, one of them must be nonzero. If not, then 0 = ( ˆu ·ˆu
1
)
2
+ ( ˆv ·ˆu
1
)
2
=
1−( ˆw ·ˆu
1
)
2
, which implies |ˆw ·ˆu
1
|=1and ˆu
1
is either ˆw or −ˆw. Similarly v
1
is either
ˆw or −ˆw. This cannot happen since ˆu
1
and v
1
are orthogonal. Let
ψ beanonzero
column of B
1
.Thevector
ζ =
ψ
⊥
satisfies the condition B
T
1
ζ =
0; therefore,
0 =
ζ
T
(r
0
B
0
ˆη
0
+ r
1
B
1
ˆη
1
) = r
0
(B
T
0
ζ)·ˆη
0
If B
T
0
ζ = (a, b), then ˆη
0
=±(b, −a)/
√
a
2
+ b
2
.Thevector ˆη
1
is determined by
ˆη
1
=1 and the linear equation
r
1
(B
T
1
ψ) ·ˆη
1
=−r
0
(B
T
0
ψ) ·ˆη
0
The ˆη
1
are therefore points of intersection, if any, between a circle and a line. The
normalization of ˆη
0
can be avoided by defining p
0
=B
T
0
ζ ˆη
0
and p
1
=B
T
0
ζ ˆη
1
.In
this case p
0
= (B
T
0
ζ)
⊥
and r
1
(B
T
1
ψ) ·p
1
=−r
0
(B
T
0
ψ) ·p
0
. The extraction of (x, y)
discussed later in fact does not require the normalizations. The intersection of line
and circle does require solving a quadratic equation, so a square root has to be
calculated (or the quadratic must be solved iteratively to avoid the cost of the square
root). A similar construction applies if det(B
0
) = 0 and det(B
1
) = 0.
If det(B
0
) = 0 and det(B
1
) = 0, then B
0
is invertible and
ˆη
0
=−(r
1
/r
0
)B
−1
0
B
1
ˆη
1
with ˆη
0
=1 and ˆη
1
=1. The extraction of (x, y) discussed later does not require
unit-length quantities for ˆη
0
and ˆη
1
, so the three equations can be rewritten to avoid
some divisions and normalizations. Rewrite the displayed equation as
r
0
det(B
0
) ˆη
0
=−r
1
Adj(B
0
)B
1
ˆη
1
Define p
0
= r
0
det(B
0
) ˆη
0
, p
1
= r
1
ˆη
1
, and C = Adj(B
0
)B
1
. The equations are now
p
0
=−C p
1
, p
0
2
= r
2
0
det(B
0
)
2
, and p
1
2
= r
2
1
.
The quadratic equations for p
1
are r
2
0
det(B
0
)
2
=p
T
1
C
T
C p
1
and p
1
2
= r
2
1
.Fac-
tor C
T
C = QEQ
T
,whereE = Diag(e
0
, e
1
) are eigenvalues and the columns of Q are
eigenvectors. Let
ψ = Q
T
p
1
. The equations become
ψ
2
= r
2
1
and r
2
0
det(B
0
)
2
=
ψ
T
E
ψ.If
ψ =(a, b), then a
2
+b
2
=r
2
1
and e
0
a
2
+e
1
b
2
=r
2
0
det(B
0
)
2
. These are two
linear equations in the two unknowns a
2
and b
2
. The formal solution is a
2
=(e
1
r
2
1
−
r
2
0
det(B
0
)
2
)/(e
1
−e
0
) and b
2
=(r
2
1
−e
0
r
2
0
det(B
0
)
2
)/(e
1
−e
0
). Assuming both right-
hand sides are nonnegative, you have four solutions (a, b), (−a, b), (a, −b), and
11.12 Miscellaneous 657
(−a, −b), as expected (intersection of ellipse and circle). Only (a, b) and (−a, b)
need to be considered; the others generate no new information in the extraction of
(x, y). Given a solution for
ψ, the corresponding nonnormalized vectors for extrac-
tion are p
1
= Q
ψ and p
0
=−C p
1
.
Solving for (x, y)
The first two equations in Equation 11.45 can be written as two systems of equations
in the unknowns x and y as
C
x
y
=
d
where ˆη
0
= (a
0
, b
0
), ˆη
1
= (a
1
, b
1
), and
C =
b
0
g
(0)
00
− a
0
g
(0)
01
b
0
g
(0)
10
− a
0
g
(0)
11
b
1
g
(1)
00
− a
1
g
(1)
01
b
1
g
(1)
10
− a
1
g
(1)
11
,
d =
a
0
g
(0)
21
− b
0
g
(0)
20
a
1
g
(1)
21
− b
1
g
(1)
20
If C is invertible, then a unique solution is obtained for (x, y).
If C is not invertible, the problem is slightly more complicated. There are no
solutions if Adj(C)
d =
0. Otherwise, the system only has one independent equation.
Since ˆη
0
=
0 and since A
T
0
R has full rank (equal to 2), the 3 × 1vectorR
T
A
0
ˆη
⊥
0
cannot be the zero vector. In fact, ˆη
⊥
0
is unit length, which implies A
0
ˆη
⊥
is unit
length. Finally, since R is a rotation matrix, R
T
A
0
ˆη
⊥
0
is a unit-length vector. The same
argument shows that R
T
A
1
ˆη
⊥
1
is a unit-length vector. Both of these conditions and
the fact that the system has infinitely many solutions implies that c
2
00
+ c
2
01
= 0 and
c
2
10
+ c
2
11
= 0.
If c
01
= 0, then y = (d
0
− c
00
x)/c
01
. Replacing this in A
T
0
R
ξ yields
A
T
0
R
ξ =
(g
(0)
00
g
(0)
11
− g
(0)
01
g
(0)
10
)x +(g
(0)
11
g
(0)
20
− g
(0)
10
g
(0)
21
)
a
0
g
(0)
11
− b
0
g
(0)
10
=: (α
0
x +β
0
) ˆη
0
Thenumeratorofα
0
is det(B
0
).Ifc
01
=0 instead, then c
00
=0, and a similar expres-
sion is obtained for A
T
0
R
ξ in terms of y, namely, α
0
y + β
0
, where the numerator of
α
0
is also det(B
0
). Similarly, if c
11
= 0, then y = (d
1
− c
10
x)/c
11
and
A
T
1
R
ξ =
(g
(1)
00
g
(1)
11
− g
(1)
01
g
(1)
10
)x +(g
(1)
11
g
(1)
20
− g
(1)
10
g
(1)
21
)
a
1
g
(1)
11
− b
1
g
(1)
10
=: (α
1
x +β
1
) ˆη
1
658 Chapter 11 Intersection in 3D
Thenumeratorofα
1
is det(B
1
).Ifc
11
=0 instead, then c
10
=0, and a similar expres-
sion is obtained for A
T
1
R
ξ in terms of y, namely, α
1
y + β
1
, where the numerator of
α
1
is also det(B
1
).
In the case c
01
= 0 and c
11
= 0, then F(x, y) reduces to
F(x, y) = r
0
|α
0
x +β
0
|+r
1
|α
1
x +β
1
|−|
φ|
If α
0
= 0 and α
1
= 0, then the minimum of F is attained at either x =−β
0
/α
0
or
x =−β
1
/α
1
. Notice that the first x forces A
T
0
R
ξ =
0, in which case the corresponding
direction must have been
d =ˆw
0
. The second x forces A
T
1
R
ξ =
0, in which case the
corresponding direction must have been
d =ˆw
1
. Both of these directions were tested
earlier, so this case can be ignored. If α
0
= 0 and α
1
= 0, then the minimum of F
is attained at x =−β
0
/α
0
. The corresponding direction must have been
d =ˆw
0
,
again handled earlier. The same argument applies to α
0
= 0 and α
1
= 0. The final
case is α
0
= α
1
= 0, in which case det(B
0
) = det(B
1
) = 0, yet another case that was
handled earlier. Therefore, these cases can be ignored in an implementation. A similar
argument applies when c
00
= 0 and c
10
= 0, and F(x, y) reduces to
F(x, y) = r
0
|α
0
y +β
0
|+r
1
|α
1
y +β
1
|−
φ
All possibilities can be ignored in an implementation since they are handled by other
separation tests. Finally, if there is a mixture of x and y terms,
F(x, y) = r
0
|α
0
x +β
0
|+r
1
|α
1
y +β
1
|−
φ
or
F(x, y) = r
0
|α
0
y +β
0
|+r
1
|α
1
x +β
1
|−
φ
then the minimization is applied in each dimension separately, but just as before,
other separation tests cover these cases. The conclusion is that an implementation
does not have to do anything when C is not invertible.
Fast Method to Test F(x, y) < 0
The two square roots, A
T
i
R
ξ, in Equation 11.43 can be avoided. The test
F(x, y) < 0 is equivalent to
r
0
A
T
0
R
ξ+r
1
A
T
1
R
ξ <
φ
The inequality can be squared and rearranged to yield the test
2r
0
r
1
A
T
0
R
ξA
T
1
R
ξ <
φ
2
− r
2
0
A
T
0
R
ξ
2
− r
2
1
A
T
1
R
ξ
2
=: ρ
11.12 Miscellaneous 659
x
y
z
P
d
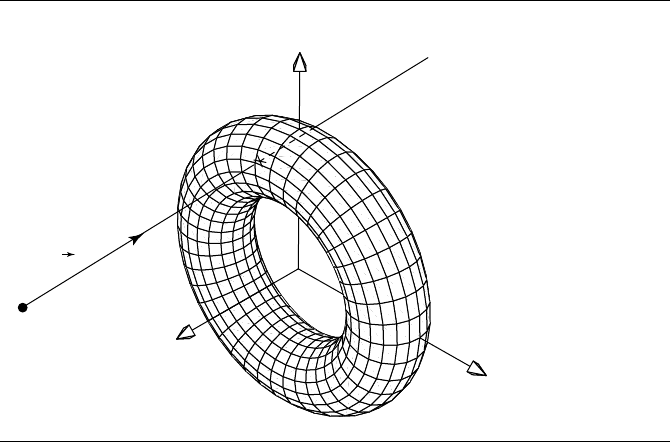
Figure 11.74 Intersection of a linear component and a torus.
If ρ ≤ 0, then F(x, y) ≥ 0 is forced, and no more work needs to be done. If ρ>0,
then squaring one more time yields the test
4r
2
0
r
2
1
A
T
0
R
ξ
2
A
T
1
R
ξ
2
<ρ
2
11.12.10 Linear Component and Torus
In this section we address the problem of intersecting a linear component with a torus
(see Figure 11.74). A linear component is defined (as usual) as an origin point and a
direction:
L(t) = P + t
d (11.46)
In the case of a line segment defined by two points P
0
and P
1
,welet
d = P
1
− P
0
.
A torus is defined implicitly:
(x
2
+ y
2
+ z
2
+ R
2
− r
2
)
2
− 4R
2
(x
2
+ y
2
) = 0 (11.47)
This defines a torus centered at the origin, and lying in the XY plane, with major
radius R and minor radius r.
660 Chapter 11 Intersection in 3D
If we substitute Equation 11.46 into Equation 11.47, we get a quartic equation in
t, of the form
c
4
t
4
+ c
3
t
3
+ c
2
t
2
+ c
1
t + c
0
= 0 (11.48)
where
c
4
= (
d ·
d)
2
c
3
= 4(P ·
d)(
d ·
d)
c
2
= 2(
d ·
d)((P ·P)− (R
2
+ r
2
)) + 4(P ·
d)
2
+ 4R
2
d
2
z
c
1
= 4(P ·
d)((P ·P)− (R
2
+ r
2
)) + 8R
2
P
z
d
z
c
0
= ((P ·P)− (R
2
+ r
2
)) − 4R
2
(r
2
− P
2
z
)
This quartic equation can be solved using a root-finding method, such as found in
Section A.5.
If the intersection is sought for purposes of ray tracing, then the desired inter-
section (there can be as many as four) will be the one closest to the ray origin P .In
addition, the surface normal at that point will also be needed, as well as the “texture
coordinates” and partial derivatives. The normal could be computed by computing
the partial derivatives of Equation 11.48 with respect to x, y, and z; however, there
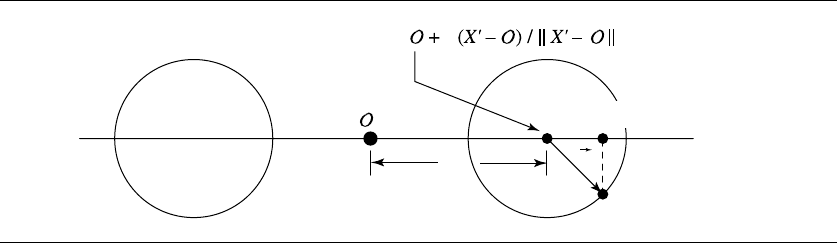
is a more direct approach. Consider the “cross section” of a torus, as shown in Fig-
ure 11.75. Because the cross section is a circle, the normal n at any point X on the
circle is simply the vector (X − C).ButC is easy to compute: the intersection point
X is projected down onto the XY plane: X
= [
X
x
X
y
0
]; then C is just at a dis-
tance R from the origin O = [
000
], along the vector (X
− O). Note that the
vector n = X − C is not normalized unless r = 1.
R
X
X' = [X
x
X
y
0]
n
C
XY plane
R
Figure 11.75 Computing the normal of a torus at a point (of intersection).
11.12 Miscellaneous 661
X' = [X
x
X
y
0]
x
y
Figure 11.76 The u parameter of a point on a torus.
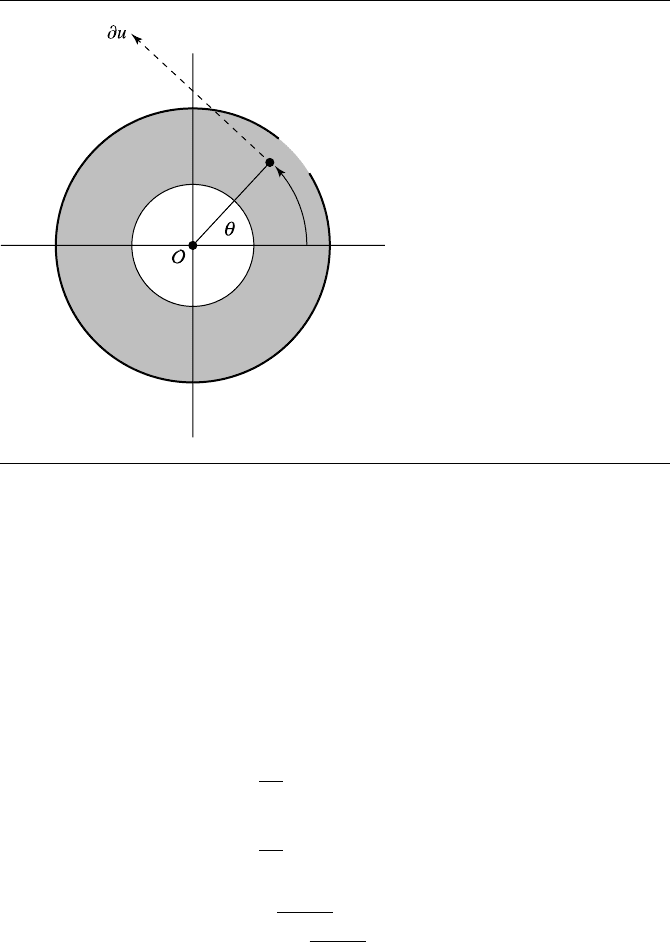
To compute texture coordinates, we’ll define the u-direction to be counterclock-
wise (as we’re looking down the z-axis), starting from the x-axis; the v-direction goes
around the circumference of the “swept tube” of the torus, starting from the inside.
Let’s start with the u parameter. Consider the cross-sectional view (this time, cutting
with the XZ plane) shown in Figure 11.76.
From this, we can easily see that a little trigonometry gives us the u parameter:
r
u
=X
− O
cos(θ) =
X
x
r
u
sin(θ) =
X
y
r
u
u =
arccos(θ )
2π
if sin(θ) ≥ 0
1 −
arccos(θ )
2π
if sin(θ) < 0
For the v-direction, consider Figure 11.77. To get cos(φ), we need the adjacent leg
and hypotenuse of the triangle—these are X
− O−R and r, respectively. Note
that if we want the parametric origin to be on the “inside” of the torus, we need to
662 Chapter 11 Intersection in 3D
X
X' = [X
x
X
y
0]
XY plane
v
r
R
Figure 11.77 The v parameter of a point on a torus.
invert (i.e., negate) the cosine. To get sin(φ), we need the length of the opposite leg
of the triangle, which is simply X
z
.So,wehave
r
v
=X
− O
cos(φ) =
−(r
v
− R)
r
sin(φ) =
X
z
r
v
u =
arccos(φ)
2π
if sin(φ) ≥ 0
1 −
arccos(φ)
2π
if sin(φ) < 0
The partial derivatives are straightforward: as is obvious from observing Fig-
ure 11.76, we have
∂u = (X
− O)
⊥
We could determine ∂v by a method similar to that used to compute the normal n,
but we can actually do this a little cheaper by simply noting that
∂v =n × ∂u
Note that the partial derivatives are computed in the local space of the torus.
They’ll need to be transformed back into world space and normalized there.

Chapter
12Miscellaneous
3D Problems
This chapter includes a variety of problems involving 3D lines, planes, tetrahedra,
and 3D circles. Most of these are commonly (or at least occasionally) encountered
problems, while others, although less commonly encountered, serve to show how
various techniques may be brought to bear on new problems.
12.1 Projection of a Point onto a Plane
In this section, we consider the projection of a point Q onto a plane P,whereP
is defined as ax + by + cz + d = 0(orP ·n + d = 0), as shown in Figure 12.1. By
definition, the line segment between Q and its projection Q
is parallel to the plane
normal n. Let the (signed) distance between the points be r;thenwehave
Q = Q
+
r n
n
(12.1)
If we dot each side with n,weget
Q ·n =
Q
+
r n
n
·n
= Q
·n +
r n
n
·n
(12.2)
663
