Schneider P., Eberly D.H. Geometric Tools for Computer Graphics
Подождите немного. Документ загружается.

774 Chapter 13 Computational Geometry Topics
// dynamic list for ear tips, reduced/updated as ears are clipped
VertexList node = vdynalist;
VertexList edynalist = empty;
for (i = 0; i < vdynaquantity; i++, node = node.Next()) {
if (node is an ear of vlist) {
VertexList tmp = node.CopySingle(); // copy only node (not links)
if (edynalist is not empty)
edynalist.InsertBefore(tmp); // tmp inserted before edynalist
else
edynalist = tmp; // first element in list
}
}
// remove ears one at a time
while (true) {
// add triangle to output list (three integer indices)
tlist.Add(vdynalist.Previous().VertexIndex());
tlist.Add(vdynalist.VertexIndex());
tlist.Add(vdynalist.Next().VertexIndex());
if (vdynaquantity == 3)
return; // last triangle was added, done triangulating
// remove the ear tip from vertex list
VertexList vprev = vdynalist.Previous();
VertexList vnext = vdynalist.Next();
vdynaquantity--;
vdynalist.RemoveSelf();
// Previous node to ear had a topological change. Recompute its
// earness.
if (vprev is an ear of vlist) {
if (vprev.VertexIndex() != edynalist.Previous().VertexIndex()) {
// removal of old ear caused vprev to be an ear
edynalist.InsertBefore(vprev.CopySingle());
}
} else {
if (vprev.VertexIndex() == edynalist.Previous().VertexIndex()) {
// removal of old ear caused vprev not to be an ear
edynalist.Previous().RemoveSelf();
}
}
// Next node to ear had a topological change. Recompute its earness.
// Advance to next vertex/ear.
13.9 Polygon Partitioning 775
if (vnext is an ear of vlist) {
if (vnext.VertexIndex() != edynalist.Next().VertexIndex()) {
// removal of old ear caused vnext to be an ear
edynalist.InsertAfter(vnext.CopySingle());
}
} else {
if (vnext.VertexIndex() == edynalist.Next().VertexIndex()) {
// removal of old ear caused vnext not to be an ear
edynalist.Next().RemoveSelf();
vnext = vnext.Next();
}
}
// get next vertex
vdynalist = vnext;
// get next ear and remove the old ear from list
edynalist = edynalist.Next();
edynalist.Previous().RemoveSelf();
}
}
It is possible to triangulate a polygon with a better asymptotic order. Much re-
search in the late 1980s and early 1990s addressed this topic. Chazelle (1991) showed
that triangulation can be done in O(n) time. However, the algorithm is complex, and
it remains to be seen if it can be implemented in a practical setting. Asymptotically
worse methods tend to be easier to implement.
13.9.3 Triangulation by Horizontal Decomposition
This section describes an O(n log n) method based on decomposition into trapezoids
whose parallel edge pairs are parallel to the x-axis (Chazelle 1991; Fournier and
Montuno 1984). The decomposition, which requires O(n log n) time, can be further
reduced in O(n) time to a small number of monotone polygons. Each monotone
polygon can be triangulated in O(n) time. Faster algorithms that use randomization
and are nearly linear are presented in Clarkson, Tarjan, and Van Wyk (1989) and
Seidel (1991). The order of these algorithms is O(n log
∗
n), where log
∗
n is defined
by iterated logarithms:
log
(i)
(n) =
n, i =0
log(log
(i−1)
n), i>0 and log
(i−1)
n>0
undefined, i>0 and log
(i−1)
n ≤ 0or log
(i−1)
n undefined
776 Chapter 13 Computational Geometry Topics
s
2
s
5
s
7
s
8
s
4
s
1
s
3
s
6
s
9
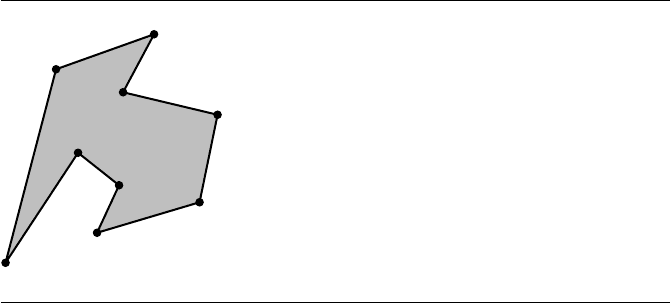
Figure 13.56 A simple polygon that is used to illustrate the horizontal decomposition into trape-
zoids. The edges are labeled randomly and are processed in that order in the figures
that follow.
The notation log
(i)
n denotes an iterated function value, not the logarithm raised to
the ith power. The final definition is
log
∗
n = min{i ≥ 0 : log
(i)
n ≤ 1}
This is a very slowly growing function. For example, log
∗
(2) = 1, log
∗
(4) = 2,
log
∗
(16) = 3, log
∗
(65536) = 4, and log
∗
(2
65536
) = 5. In practical applications, effec-
tively log
∗
n is a small constant. The randomized algorithms mentioned above are,
practically speaking, O(n). A brief description of the algorithm is presented in Paeth
(1995), in the article “Fast Polygon Triangulation Based on Seidel’s Algorithm.” The
polygon example, shown in Figure 13.56, used to illustrate the ideas is taken from
Figure 1 in that article.
Horizontal Decomposition
The idea is to construct a set of horizontal strips by sorting the y-values of the poly-
gon vertices. The y-values can be sorted directly with an array-based O(n log n) sort,
but by randomizing the edges and processing one at a time using a dynamic struc-
ture such as a binary search tree, the expected order is asymptotically better. Within
each strip, the subpolygons are decomposed into trapezoids, each strip managing a
dynamic structure such as a binary search tree to allow incremental sorting of the
trapezoids. It is convenient to think of the polygon as decomposing the entire plane.
This makes handling boundary conditions of the strips and trapezoid lists easier in
the implementation.
13.9 Polygon Partitioning 777
00
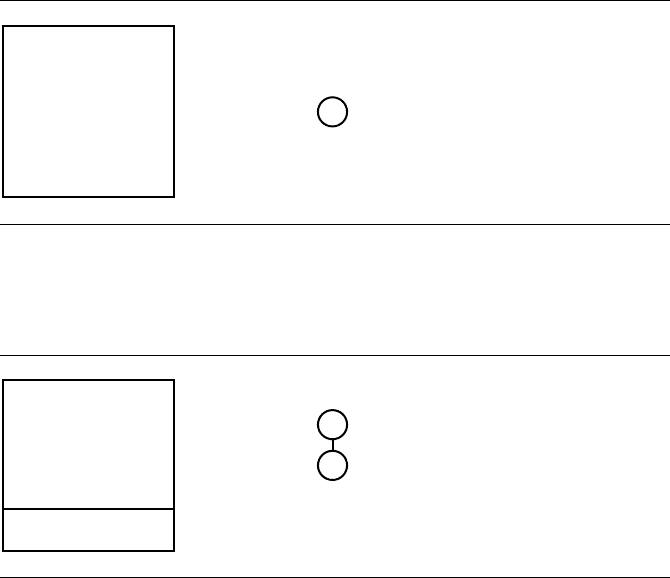
Figure 13.57 The entire plane is a single trapezoid.
1
0
0
1
Figure 13.58 Split by s
1
.y
0
.
We will describe the algorithm by example using the polygon in Figure 13.56.
The polygon vertices are assumed to be counterclockwise ordered. We will give the
pseudocode after the example. The entire xy-plane will be represented in this exam-
ple as a rectangle. Initially, the first strip and first trapezoid T
0
are the entire plane,
as illustrated in Figure 13.57. In each of the following figures, the geometric view of
the decomposition is on the left and the corresponding graph of trapezoids is on the
right.
An edges s
k
has end points (x
0
, y
0
) and (x
1
, y
1
). The components are designated
by s
k
.x
0
, s
k
.y
0
, s
k
.x
1
, and s
k
.y
1
. The first edge to be processed is s
1
.They-value s
1
.y
requires the current strip to be partitioned into two strips, each strip containing
a trapezoid that represents a half-plane (see Figure 13.58). The value s
1
.y
1
causes
another strip split, each strip containing an unbounded trapezoid (see Figure 13.59).
The edge s
1
is inserted, so to speak, into the data structures. The insertion causes the
single trapezoid of the middle strip to be partitioned into two trapezoids (see Figure
13.60).
778 Chapter 13 Computational Geometry Topics
2
1
0
0
1
2
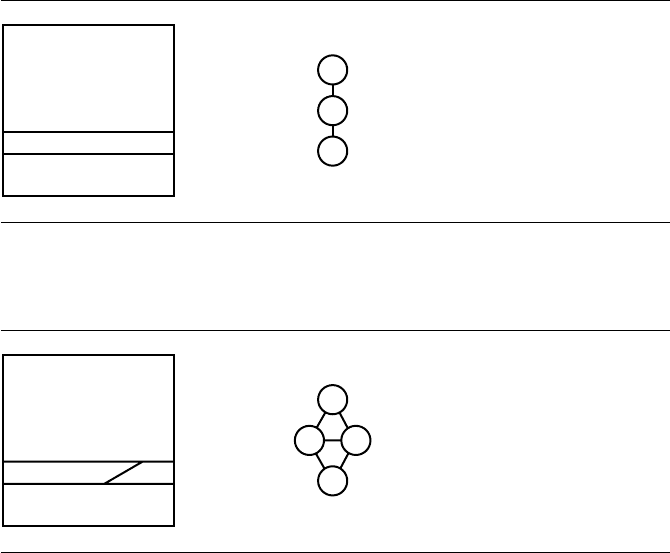
Figure 13.59 Split by s
1
.y
1
.
23
1
0
0
1
32
Figure 13.60 Insert s
1
.
Edge s
2
is the next to be processed. The value s
2
.y
1
forces a split (see Figure 13.61).
The value s
2
.y
0
forces a split (see Figure 13.62). Insertion of s
2
forces partitioning of
trapezoids in the three strips that the edge spans (Figure 13.63).
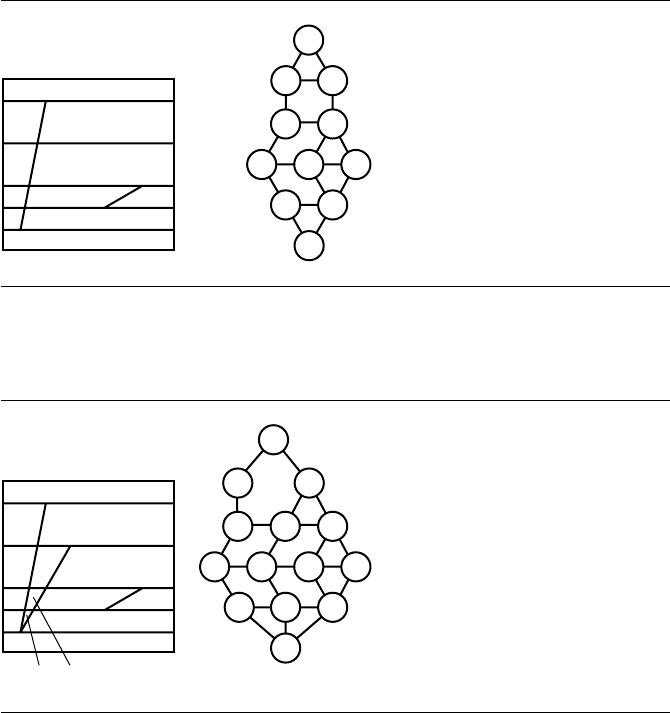
Edge s
3
is the next to be processed. The value s
3
.y
1
forces a split (see Figure 13.64).
The value s
3
.y
0
= s
2
.y
1
, which was already processed, so no splitting occurs. The
insertion of s
3
forces partitioning of trapezoids in the strips that the edge spans (see
Figure 13.65).
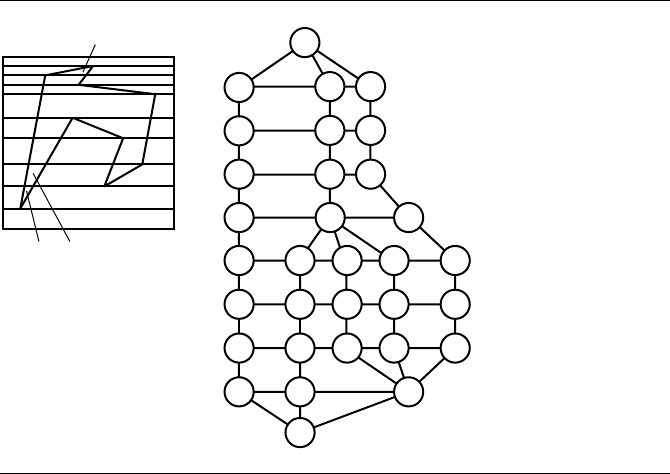
The remaining edges are processed in a similar manner. Edge s
9
is the final edge to
be processed. Its insertion forces partitioning of trapezoids in the strips that the edge
spans (see Figure 13.66). Observe that the plane has been partitioned into a finite
number of strips and that each strip consists of a finite number of trapezoids. The
data structure uses binary search trees, both for strips and for trapezoids within a
strip. This data structure can be used for O(log n) point-in-polygon queries. Given
a test point, its y-value is used to search the binary search tree for the strips to find
the strip that contains that y-value. If the y-value is on a strip boundary, either strip
sharing that boundary can be used. The binary search tree for the trapezoids stores
the line equations for the left and right boundaries of the trapezoids. The x-value
13.9 Polygon Partitioning 779
23
1
0
0
4
1
32
4
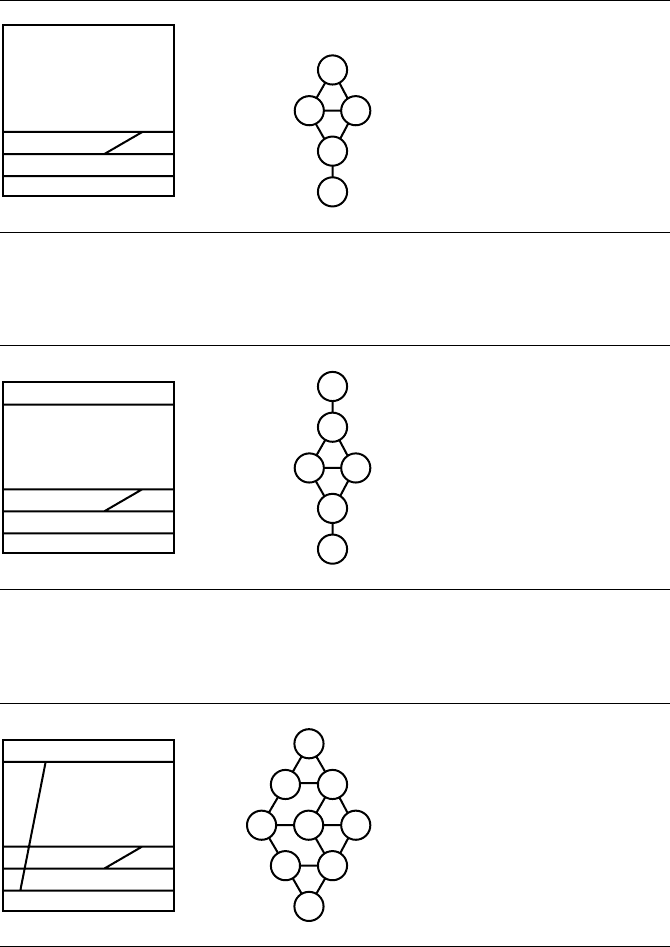
Figure 13.61 Split by s
2
.y
1
.
23
1
0
0
4
1
5
32
4
5
Figure 13.62 Split by s
2
.y
0
.
237
16
0
8
4
5
0
4
1
5
32
6
8
7
Figure 13.63
Insert s
2
.
780 Chapter 13 Computational Geometry Topics
237
16
9
5
10
4
8 0
0
4
1
5
32
6
8
910
7
Figure 13.64 Split by s
3
.y
1
.
23127
16 11
9
1310
4
0
4
1
5
32
6
8
910 13
11
7
12
8 0
5
Figure 13.65 Insert s
3
.
of the test point is compared against those lines to determine in which trapezoid the
point lies. If the test input point is on a strip boundary, comparisons should use strict
inequality whenever the trapezoid is an “outside” trapezoid. The inside/outside tag is
easy to assign given the way that the polygon edges were used to partition the strips.
The pseudocode for the top-level call that constructs the strips and trapezoids
is listed below. The
Strip object supports a binary search tree data structure and
additionally has three members, the minimum y-value of the strip
min, the maximum
y-value of the strip
max, and a binary search tree of Trapezoid objects ttree.The
Trapezoid object also supports a binary search tree data structure and additionally has
three members, the polygon edge index corresponding to its left edge
min, the polygon
edge index corresponding to its right edge
max, and a direction indicator classify
13.9 Polygon Partitioning 781
17 14
2529
27 0
18
5
26
8
19
916
202131
2413
4
1
30 2
3
6
23
10
15
22
11
7
12
28
10
22
4
6 11
7 12
23
15 17 14
26
8
19
1
30
31
2413 16
21
29
27
0
25
28
5
18
3 2
20
9
Figure 13.66 Insert s
9
.
that is +1 if the interior of the polygon at the maximum edge is in the positive x-
direction or −1 if the interior of the polygon at the minimum edge is in the negative
x-direction.
void Decompose(int N, Point P[N])
{
// randomly permute edges
int index[N] = PermuteRange(0,N-1);
// prototypes: Strip(min, max, ttree), Trapezoid(min, max, classify)
S = new Strip(-infinity, +infinity, new Trapezoid(-infinity, +infinity, -1));
for (i0 = 0; i0 < N; i0++) {
i1 = (i0 + 1) mod N;
if (P[i0].y < P[i1].y)
Insert(S,P[i0].y, P[i1].y, i, -1); // interior in negative x-direction
else if ( [i1].y < P[i0].y)
Insert(S,P[i1].y, P[i0].y, i, +1); // interior in positive x-direction
// else ignore horizontal edges
}
}
782 Chapter 13 Computational Geometry Topics
The strip insertion pseudocode is
void Insert(Strip S, float y0, float y1, int i, int classify)
{
// binary search for strip containing y0, assumes S0 = [min, max)
S0 = Locate(S, y0);
if (y0 > S0.min) {
// y0 interior to strip, split to N = [min, y0), S0 = [y0, max)
N = new Strip(y0, max, S0.CopyOfTTree());
S0.min = y0;
S0.InsertBefore(N); // insert N before S0 in search tree
}
// binary search for strip containing y1, assumes strip is min <=y<max
S1 = Locate(S, y1);
if (y1 > S1.min) {
// y1 interior to strip, split to S1 = [min, y1), N = [y1, max)
N = new Strip(y1, max, S1.CopyOfTTree());
S1.max = y1;
S1.InsertAfter(N); // insert N after S1 in search tree
}
// add a trapezoid to each strip spanned by edge
for (L = S0; L <= S1; L++)
Insert(L.ttree, (L.min + L.max) / 2, i, classify);
}
The trapezoid insertion pseudocode is
void Insert(Trapezoid T, float mid, int i, int classify)
{
// Locate correct place to insert new trapezoid by comparing x-values
// along the mid line passing through the trapezoids.
T0 = LocateMid(T, i);
// Split T0 = {min,max} to N = {min,i} and T0 = {i,max}
N = new Trapezoid(T0.min, i, classify);
T0.min = i;
T0.classify = -classify;
T0.InsertBefore(N); // insert N before T0 in search tree
}
The pseudocode supports construction of the point-in-polygon query data struc-
ture. To support triangulation, trapezoids that are vertically adjacent must be merged.
13.9 Polygon Partitioning 783
17
2529
27
0
5
19
9
16
21
24
11
4
1
30
2
3
6
28
6
19
25
0
17
29
27
28
11 1624 9
30
21
5
2
31
4
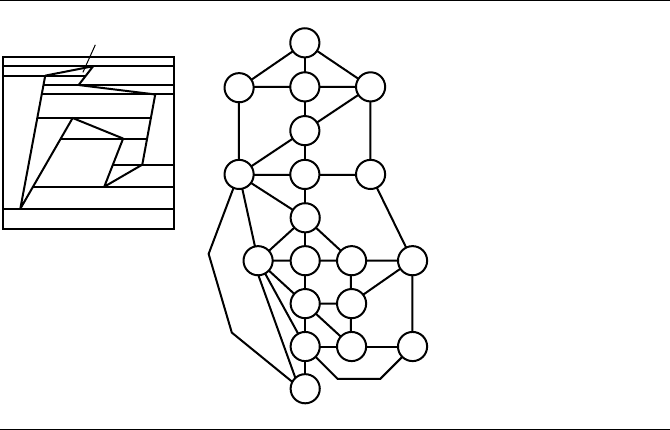
Figure 13.67 The plane after trapezoids are merged into maximally sized ones.
This requires adding to the
Trapezoid object two list members that store links to
trapezoids vertically adjacent at the strip minimum edge and at the strip maximum
edge. The pseudocode must be modified accordingly to construct those links.
Monotone Polygon Construction
The next phase in the triangulation is to construct monotone polygons whose union
is the original polygon. The first step in this process is to merge the trapezoids into
maximally sized ones. Figure 13.67 shows the merged configuration for the plane.
The figure shows the exterior trapezoids merged. However, for the purposes of tri-
angulation, only the interior trapezoids are required. Figure 13.68 shows the merged
trapezoids only for the polygon itself.
The second step is to add line segments connecting polygon vertices. These seg-
ments and the original polygon edges form a decomposition into monotone polygons
where the monotonicity is relative to the y-direction. Suppose that the original poly-
gon has no two vertices with the same y-value. Each trapezoid in the horizontal
decomposition of that polygon contains exactly two vertices of the polygon, one on
its top edge and one on its bottom edge. If the vertex is an edge-interior point, it must
be a cusp. That is, the two edges that share the vertex are either both above or both
below the horizontal line of the vertex. A cusp that opens downward occurs on the
bottom edge of some trapezoid. A line segment is added from that cusp to the vertex
