Сергеев В.Л. Интегрированные системы идентификации
Подождите немного. Документ загружается.


21
где
k
α
– векторы столбцы дополнительных априорных данных, получен-
ных с
1
s
объектов-аналогов с ошибками
k
η
;
l
y
– векторы столбцы допол-
нительных априорных данных с
2
s объектов-аналогов, заданных с ошиб-
ками
k
ν
; F – конечно-разностный оператор;
(), ( )
ti t j
yyti tj
−−
=
−=−xx
–
начальные условия;
1
k
Г
,
2l
Г
– индикаторные диагональные матрицы
вида (1.4.8).
3. Линейные непараметрические интегрированные системы моде-
лей
. Линейные непараметрические интегрированные системы моделей
основаны на линейных статических либо динамических моделях объек-
та и на непараметрических статических либо динамических моделях
объектов-аналогов.
В качестве примера линейной непараметрической статической ин-
тегрированной системы моделей, в которой дополнительная априорная
информации о параметрах модели и выходе объекта представлена клас-
сами непараметрических моделей, приведем
уравнения:
*
1
2
;
() ;
() ,
f
f
⎧
=+
⎪
=
+
⎨
⎪
=
+
⎩
yFαξ
ααη
yy
ν
(1.4.13)
где
1
f
,
2
f
–неизвестные, однозначные, ограниченные функции.
Данная интегрированная система моделей является естественным
представлением моделей дополнительных априорных данных, посколь-
ку часто не удается найти подходящее конечномерное параметрическое
описание связи исследуемых объектов и объектов-аналогов.
4. Нелинейные непараметрические интегрированные системы мо-
делей
. Нелинейные непараметрические интегрированные системы мо-
делей основаны на нелинейных статических либо динамических моде-
лях объекта и на непараметрических статических либо динамических
моделях объектов-аналогов.
В качестве примера нелинейной непараметрической статической
интегрированной системы моделей,
по аналогии с (28), рассмотрим
уравнения:
*
1
2
(, ) ;
() ;
() ,
f
f
f
⎧
=
+
⎪
=+
⎨
⎪
=+
⎩
yxα
ξ
ααη
yy
ν
(1.4.14)
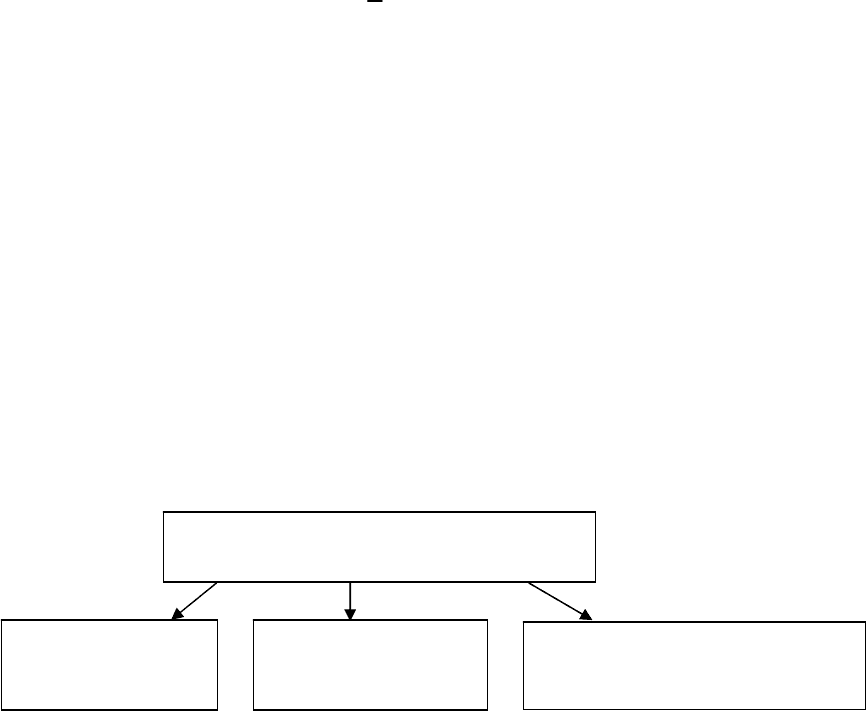
где
),( αxf
– известная нелинейная функция регрессии.
22
5. Непараметрические интегрированные системы моделей. Непа-
раметрические интегрированные системы моделей основаны на непара-
метрических статических либо динамических моделях объекта и на не-
параметрических статических либо динамических моделях априорной
информации. Непараметрическую статическую стохастическую систему
с одним объектом-аналогом (модель двух черных ящиков) можно пред-
ставить в виде:
*
1
2
() ;
() ,
f
f
⎧
=+
⎨
=
+
⎩
yxξ
Гyxη
(1.4.15)
где
1
f
,
2
f
– неизвестные однозначные функции; Г – известная индика-
торная матрица.
Данная интегрированная система моделей часто используется в
случаях, когда объект слабо изучен либо достаточно сложный для его
параметрического описания. С другой стороны и дополнительную ап-
риорную информацию о выходе объекта не удается представить в виде
конечномерного параметрического описания. Классические методы не-
параметрического оценивания функций приведены в
приложении 3.
1.5. Структура интегрированной системы идентификации
Под интегрированной системой идентификации понимается систе-
ма разработки (проектирования) оптимальной, в смысле заданных кри-
териев качества, интегрированной системы моделей. Структура интег-
рированной системы идентификации представлена на рис. 1.4.
Рис. 1.4
Интегрированные системы моделей достаточно подробно изложе-
ны в предыдущем разделе, поэтому ниже рассматриваются только кри-
терии качества и оптимальности интегрированных систем моделей и ал-
горитмы адаптации.
Критерии качества и оптимальности. Комбинированные крите-
рии качества интегрированной системы моделей, состоящие из комби-
нации частных критериев, предназначены для объединения (слияния)
моделей объекта и моделей объектов-аналогов.
Интегрированная система
идентификации
Интегрированная
система моделей
Критерии качества
и оптимальности
Алгоритмы адаптации (решение
оптимизационных задач)

23
Частные критерии качества представляют меры близости измерен-
ных значений выходных переменных исследуемого объекта и объектов-
аналогов к их соответствующим значениям, полученным на основе мо-
делей.
В случае одной выходной переменной для оценки близости объекта
и его модели, оценки близости дополнительных априорных данных их
моделям вводится функция (функционал) потерь
(,)rUV
, обладающая
свойствами расстояния:
1.
. ;0),( VUVUr ≠∀>
2.
. ;0),( VUVUr =∀=
3.
.,, );,(),(),( ZVUVZrZUrVUr
∀
+≤
Например, средние потери от отклонения модели объекта
)(ty
от
соответствующих отклонений выхода объекта
)(
*
ty
на интервале
[0, ]T
будут равны
*
0
1
() ( (),())d,
T
ry t yt t
T
=
∫
Q α
(1.5.1)
где
)),(()( αtxfty =
; r – функция потерь.
В данном случае задача оптимизации заключается в определении
вектора параметров
α
*
модели объекта, который бы минимизировал
средние потери
*
arg min ( ),
m
R∈
=
α
α Q α
(1.5.2)
где
arg min ( )
m
R∈α
Q α
означает точку минимума функционала средних потерь
)
(αQ
.
Сформулированный критерий оптимальности переводит процедуру
определения параметров функции в задачу оптимизации. Функционал
средних потерь часто называют критерием качества модели объекта ли-
бо просто критерием качества.
Предполагая аддитивный характер ошибок измерения выхода
объекта
*
(,) , 1,
iii
yfx i n=+ξ=α
,
функционал качества часто выбирают в виде
*
11
() ( ( ,)) (ξ ).
nn
ii i
ii
ry f r
==
=− =
∑∑
Q α x α
(1.5.3)
Выбор функции потерь
r определяется вероятностно-статистическими
характеристиками случайных ошибок (помех)
, 1,
i
inξ=
Например,
при независимости и нормальности ошибок
ξ , 1, ,
i
in=
имеющими ог-
раниченную дисперсию
2
, 1,
i
inσ=σ<∞ =
, оптимальной является
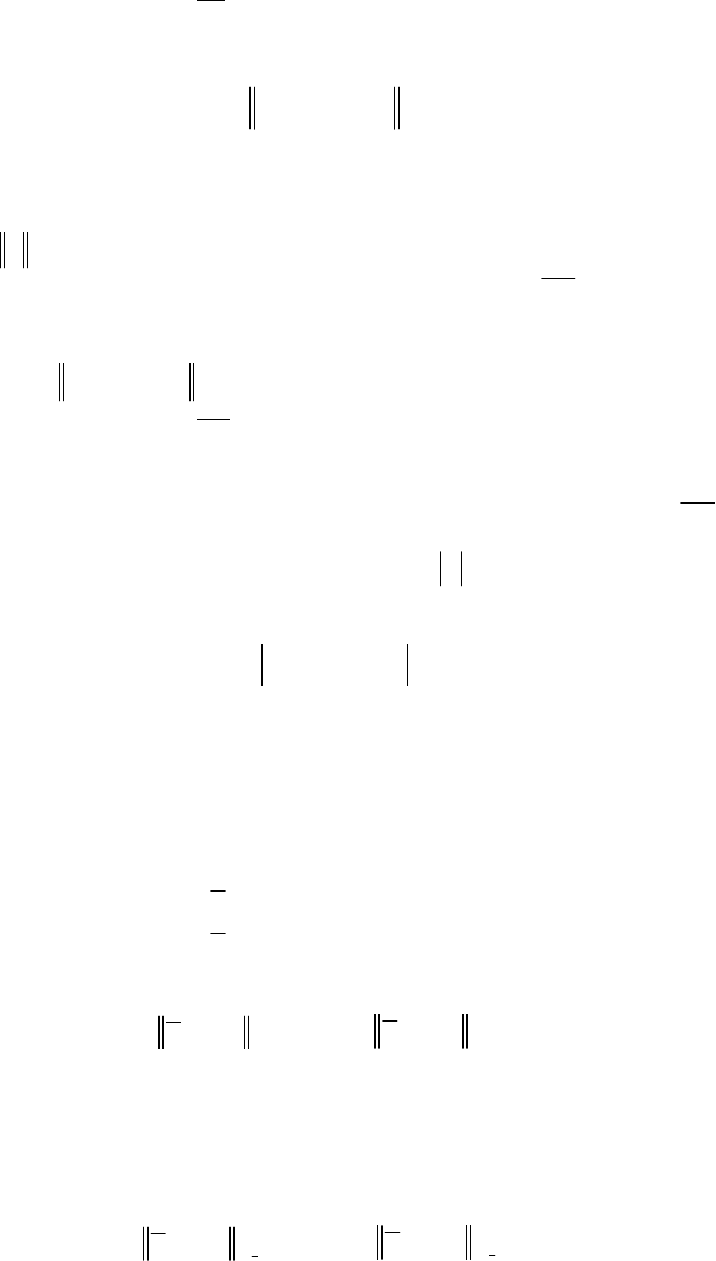
24
функция потерь
2
(ξ ) ξ , 1,
ii
rin== [15, 22], и критерий качества (1.5.3) пе-
реходит в широко используемый квадратичный критерий
2
2*
1
() ( )
n
T
i
i
f,
=
=ξ= − =
∑
Q α yxαξξ
, (1.5.4)
где
*
y
– вектор измеренных значений выхода объекта;
),( αxf
– вектор-
столбец значений выхода объекта, полученный на основе модели объек-
та в точках;
x
– норма вектора x.
Часто используется взвешенный с весами
njiw
ij
,1, , =
квадратич-
ный функционал качества
2
** *
() (,) ( (,)) ( (,))
y
T
y
W
fff=− =− −Q α yxα yxα Wy xα
, (1.5.5)
где матрица
),1,,( njiw
ijy
==W
определяется статистическими харак-
теристиками вектора случайных величин
y
*
.
Если распределение плотности вероятности величины
, 1,
i
inξ=
равно распределению Лапласа
22
( ) exp( / 2 )fx x
−
=
σ−σ
, то оптималь-
ным является критерий качества [21]
∑
=
−=
n
i
ii
xfy
1
*
),()( ααQ
. (1.5.6)
Частные критерии качества объектов-аналогов формируем по ана-
логии с рассмотренными функционалами качества. Например, для ли-
нейной интегрированной системы моделей с учетом априорной инфор-
мации о выходе объекта и параметрах модели объекта
*
1
2
;
;
,
⎧
=+
⎪
=+
⎨
⎪
=+
⎩
yFαξ
α Rαη
yHyη
(1.5.7)
частные квадратичные критерии качества объектов-аналогов равны
2
1
()=−J ααRα
,
2
2
() .=−J α yHy
(1.5.8)
При использовании данных критериев качества предполагается,
что векторы ошибок задания дополнительных априорных данных
η
1
и
η
2
распределены по нормальному закону.
При наличии априорной информации о статистических характери-
стиках ошибок
η
1
, η
2
следует использовать взвешенные критерии вида
2
1
()=−
α
W
J ααRα
,
2
()=−
y
W
J α yHy
, (1.5.9)

25
где
α
W
,
y
W
– матрицы, связанные со статистическими характеристи-
ками случайных величин
α
,
y
.
В качестве критерия качества интегрированной системы моделей
будем использовать взвешенные частные критерии качества вида:
)(β)()(
1
αJαQαΦ
j
m
j
j
∑
=
+=
, (1.5.10)
где
)(αQ
– частный критерий качества модели исследуемого объекта;
()
j
J α
– частные критерии качества моделей объектов-аналогов; β
j
–
управляющие переменные, определяющие вес дополнительных априор-
ных данных.
Следует отметить, что решение разнообразных задач обработки экс-
периментальных данных, идентификации, оптимизации и управления
связано с использованием взвешенных критериев качества вида (1.5.10).
Например, при решении задач оптимизации функций при наличии огра-
ничений функционал типа
)(αΦ
называют функцией Лагранжа, а управ-
ляющие переменные β
j
имеют смысл множителей Лагранжа [19–20].
При решении обратных некорректно поставленных задач [19]
функционал
)(αΦ
имеет смысл регуляризирующего (сглаживающего)
критерия, а частные функционалы
mj
j
,1 , =J
имеют смысл стабилизи-
рующих функционалов, связанных с «гладкостью» искомого решения.
Так, например, при определении ИПФ
)(tk
интегрального уравне-
ния (1.2.8) в качестве стабилизирующего функционала используют [19]
2
0
d()
d
d
T
kt
t
t
⎡
⎤
=
⎢
⎥
⎣
⎦
∫
J
.
Новым в приведенной структуре взвешенного функционала (1.5.10)
является наличие механизма, позволяющего учитывать разнородную
дополнительную априорную информацию.
Оптимальная структура интегрированной системы моделей опре-
деляется критерием вида
** * *
,,,
(), , arg min (,,,)
mm
RfFfF R
f
fff
∈∈∈∈
=
αβ
αβ Φα β
, (1.5.11)
где
*
f
и
*
f
представляют оптимальные функции из множества функ-
ций
F,
F
, используемых, соответственно, в качестве моделей иссле-
дуемого объекта и моделей объектов-аналогов;
)(
**
βα
– оптимальные
параметры модели объекта;
β
*
– оптимальные значения управляющих
параметров.

26
Получение оптимальной структуры интегрированной системы мо-
делей (1.5.11) представляет достаточно сложную задачу проектирова-
ния, которую, как правило, решают последовательно:
1. При заданной структуре моделей исследуемого объекта и объек-
тов-аналогов получают оптимальные оценки неизвестных параметров
*
() argmin (, , ,)
m
R
ff
∈
=
α
αβ Φα β
.
(1.5.12)
2. Определяют оптимальные значения управляющих параметров
*
arg min ( , , , )
R
f
f
∈
=
β
βΦαβ
. (1.5.13)
3. Определяют оптимальные модели объекта и оптимальные моде-
ли объектов-аналогов
*
***
,
,argmin(,,,)
fFfF
ff ff
∈∈
= Φα β
. (1.5.14)

27
Глава 2
ЛИНЕЙНЫЕ ИНТЕГРИРОВАННЫЕ СИСТЕМЫ ИДЕНТИФИКАЦИИ
2.1. Линейные интегрированные системы идентификации с учетом
априорной информации о параметрах модели объекта
Фундаментальной проблемой, лежащей в основе решения многих
практических задач, является создание интегрированной системы иден-
тификации на основе линейных статических либо динамических интег-
рированных систем моделей с учетом дополнительной априорной ин-
формации. Остановимся на рассмотрении линейной статической стохас-
тической интегрированной системы моделей с учетом дополнительной
априорной информации вида:
*
111 212 1
121 222 2
11 2 2
*
1
1
1
1
*
2
*
2
2
2
*
,
,
(), (), ,( )
(), (), ,( )
(), (), ,( )
α
α
ξ
α
ξ
α
,,,
α
ξ
α
m
m
m
m
mnm
nn
m
m
n
fx fx f x
fx f x f x
fx f x f x
y
y
y
⎧
⎪
⎨
⎪
⎩
⎡⎤
⎢⎥
⎢⎥
⎢⎥
⎢⎥
⎢⎥
⎣⎦
⎡⎤
⎡⎤
⎡⎤
⎢⎥
⎢⎥
⎢⎥
⎢⎥
⎢⎥
⎢⎥
⎢⎥
⎢⎥
⎢⎥
⎢⎥
⎢⎥
⎢⎥
⎢⎥
⎢⎥
⎢⎥
⎣⎦
⎣⎦
⎣⎦
=+
=+
=
== ==
yFαξ
α Rαη
F
y ααξ
1
2
m
n
η
η
,,
η
⎡⎤
⎡
⎤
⎢⎥
⎢
⎥
⎢⎥
⎢
⎥
⎢⎥
⎢
⎥
⎢⎥
⎢
⎥
⎢
⎥
⎢⎥
⎣
⎦
⎣⎦
=η
(2.1.1)
где
F – матрица значений известных функций ))(),...,(),(()(
21
xxxxf
m
fff
=
,
вычисленных в точках
ni
i
,1, =x
(предполагаем, что входные перемен-
ные объекта измеряются точно);
T
n
yyy ),,,(
**
2
*
1
*
…=y
– вектор измерен-
ных значений выхода объекта;
α – вектор неизвестных значений пара-
метров;
12
(α , α ,,α )
T
m
=α …
– вектор значений априорной дополнитель-
ной информации о параметрах модели объекта;
),1,,( mjir
ij
==R
– из-
вестная квадратная матрица;
ξ, η – векторы случайных величин, пред-
ставляющие ошибки измерения выхода объекта и ошибки задания ап-
риорной информации;
Т – символ транспонирования.
Проектирование оптимальной структуры интегрированной систе-
мы моделей сводится к выбору критерия качества и синтезу алгоритмов
адаптации, которые в данном случае заключаются в решении оптимиза-
ционных задач по определению вектора неизвестных параметров
12
(α ,α ,,α )
T
m
=α … .
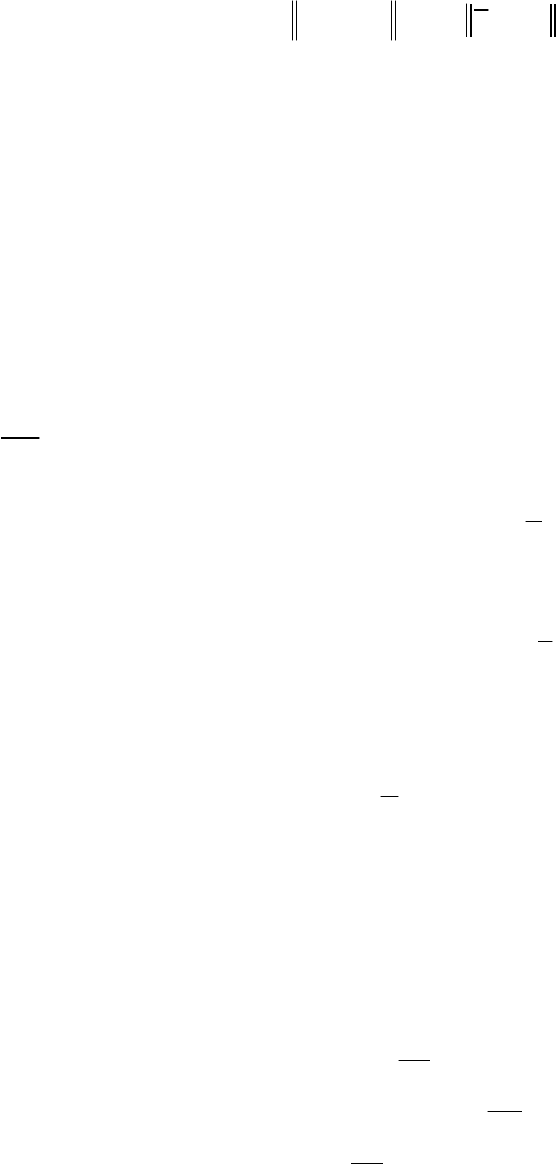
28
Рассмотрим решение оптимизационной задачи с использованием
частных квадратичных критериев качества, принимая в качестве оценки
параметров
α величину:
2
2
*
*
() argmin( β )
y
α
β
==+=−+−
W
W
α
αΦJQ y FααRα
, (2.1.2)
где
Ф – комбинированный взвешенный критерий качества интегриро-
ванной системы идентификации;
QJ,
– частные критерии качества мо-
дели исследуемого объекта и модели объекта-аналога;
y
W
и
α
W
– не-
которые неотрицательно определенные матрицы, β – управляющий па-
раметр. Отметим, что задачу определения параметров
α часто называют
обратной задачей.
Для решения задачи (2.1.2) необходимо взять производные по па-
раметрам
α, используя формулы для производных по векторному аргу-
менту, приведенные в приложении 1 и приравнять их к нулю:
*
2( )2 ( )0.
TT
y
−
∂
=
∇=− − − − =
∂
αα
Φ
Φ FW y Fα RW α Rα
α
В результате получаем систему линейных алгебраических уравнений
)β()β(
T*TTT
αWRyWFαRWRFWF
αα
+
=
+
yy
(2.1.3)
относительно вектора неизвестных параметров
α.
Решение системы уравнений (2.1.3) можно представит в виде
*T T1T*T
(β)( β )( β ).
yy
αα
−
=+ +α FWF RWR FW
y
RWα
(2.1.4)
Следует отметить, что при использовании квадратичных критериев
качества, оптимизационная задача (2.1.2) имеет аналитическое решение.
Линейные интегрированные системы идентификации в зависимо-
сти от выбора матриц
R
,
y
W
,
α
W
, вектора
α
и управляющего парамет-
ра β, с учетом имеющейся априорной информации, порождают доста-
точно широкий спектр алгоритмов идентификации. Приведем соответ-
ствующие примеры:
1. Обобщенные оценки метода наименьших квадратов (МНК). При
β = 0 из (2.1.4) следуют обобщенные оценки наименьших квадратов [1–4]:
*T1T*
)( yWFFWFα
yy
−
= , (2.1.5)
где под матрицей
1−
=
ξy
VW
=
1
),1,),ξξ(cov(
−
= nji
ji
понимается обратная
корреляционная матрица случайных величин
ni
i
,1,ξ =
с нулевыми ма-
тематическими ожиданиями (
ni
i
,1,0ξ ==M
).

29
При
I=
ξ
W
(где I – единичная матрица) и β = 0 из (2.1.4) следуют
оценки метода наименьших квадратов
*T1T*
)( yFFFα
−
=
. (2.1.6)
2. Регуляризированные по Тихонову алгоритмы и Ridge-приближения.
Пусть в
y
I
α
===RW W
и
α
= 0. Тогда оценка (2.1.4) совпадает с регу-
ляризированной по Тихонову оценкой
*1T*
)β()β( yFIFFα
T−
+=
(2.1.7)
для решения систем линейных уравнений
TT*
()( ),=FFα F
y
полученной
при решении оптимизационной задачи вида
2
2
*T
,
β
=− +⋅Φ yFαα
(2.1.8)
где величина
2
β α⋅
играет роль стабилизирующего функционала, кото-
рый представляет уклонение решения от начала координат и позволяет
получить устойчивые решения задачи идентификации линейных сис-
тем при вырожденной матрице
FF
T
. Следует также отметить, что
функционал (2.1.8) является частным случаем функционала для интег-
рированной системы моделей (2.1.1) в случае равенства нулю допол-
нительных данных о векторе оцениваемых параметров объекта. Оцен-
ка (2.1.7) получила название гребневой Ridge-оценки параметров ли-
нейной регрессии [15].
3. Байесовские оценки параметров линейных систем. При
1
ξ
,
y
−
=WV
1
αα
,,M,β 1,
−
====WVRΙα α
где
1
α
−
V
– обратная корреляционная мат-
рица априорного распределения случайного вектора параметров α оцен-
ка (2.1.4) примет вид
*T1 11T1*1
ξα ξ α
()( M)
−−−− −
=+ +α FV F V FV y V α
. (2.1.9)
Приближение (2.1.9) представляет Байесовскую оценку параметров
линейной регрессии, полученных методом максимума апостериорной
вероятности приведенного в приложении 3, где в качестве априорной
информации используются данные о среднем значении
M=αα случай-
ного параметра α, распределенного по нормальному закону с известной
корреляционной матрицей V
α
.
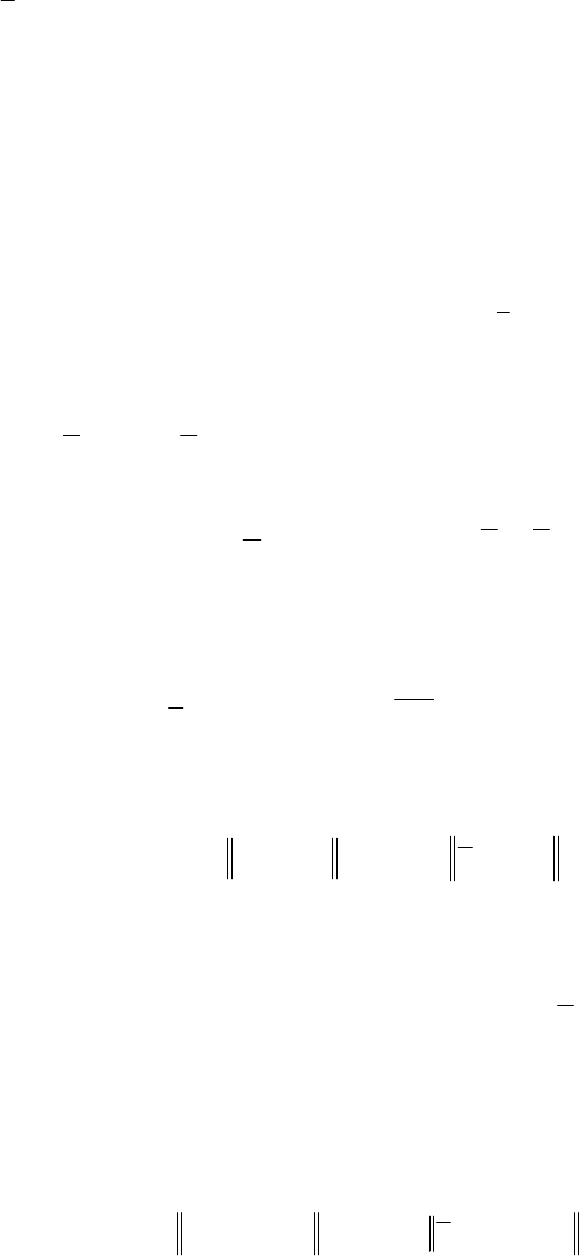
Следует отметить, что Байесовская оценка параметров регрессии
порождается интегрированной стохастической системой моделей вида
⎩
⎨
⎧
+=
+=
ηαα
ξFαy
M
,
*
(2.1.10)
и использованием частных квадратичных критериев качества.
30
4. Алгоритмы метода статистической регуляризации. При
I
=
R
,
1
ξ
,M:
y
−
==WVαα
*T1 1T1*
ξαξ α
(β)( β )( β M)
−−−
=+ +α FV F W FV
y
W α
. (2.1.11)
Приближение (2.1.4) представляет статистически регуляризированную
оценку в условиях неполной априорной информации о корреляционной
матрице априорного распределения
α
W
[20].
5. Алгоритмы идентификации при наличии ограничений на пара-
метры.
При W
α
= I и η = 0 (случайная составляющая в априорных дан-
ных отсутствует), оценка (2.1.11) соответствует решению задачи иден-
тификации при наличии ограничений типа равенств
:
=
α Rα
)β()β(),β(
T*1
ξ
T1T1
ξ
T*
αRyVFRRFVFαα ++=
−−−
. (2.1.12)
Следует отметить, что при наличии линейных ограничений типа
неравенств
k≤−− )()(
T
ααRαα
оценка параметров α является мини-
максной и имеет вид
ααFyVFRFVFα +−+=
−−−
)()()(
T*1T11T*
1
ξξ
k
k
. (2.1.13)
Рассмотрим интегрированную систему моделей, где априорные сведе-
ния о параметрах модели объекта формируются с
d объекта-аналога:
*
, 1, .
kk k
kd
⎧
=+
⎪
⎨
=+ =
⎪
⎩
yFαξ
α R αη
(2.1.14)
Для данной системы в качестве оптимальной оценки вектора неизвест-
ных параметров α будем использовать величину:
2
*T
2
1
*
(β)argmin( β )
y
d
kk k
k
α
=
==−+−
∑
W
W
α
αΦyFααR α
.
Вычисляя соответствующие производные и приравнивая их к нулю, по-
лучим систему линейных уравнений
)β()β(
1
*T
1
T
∑∑
=
αα
=
+=+
d
k
kkkyk
T
kk
d
k
y
αWRyWFαRWRFWF
(2.1.15)
для определения вектора параметров α.
Завершающим этапом адаптации линейной интегрированной систе-
мы моделей (2.1.1), (2.1.14) является задача определения оптимальных
управляющих параметров
22
****
k
1
arg min( ( *( )) ( ) β () )
y
d
kk
R
k
α
∈
=
==−+−
∑
WW
β
βΦαβyFαβ α R αβ
. (2.1.16)
