Сергеев В.Л. Интегрированные системы идентификации
Подождите немного. Документ загружается.

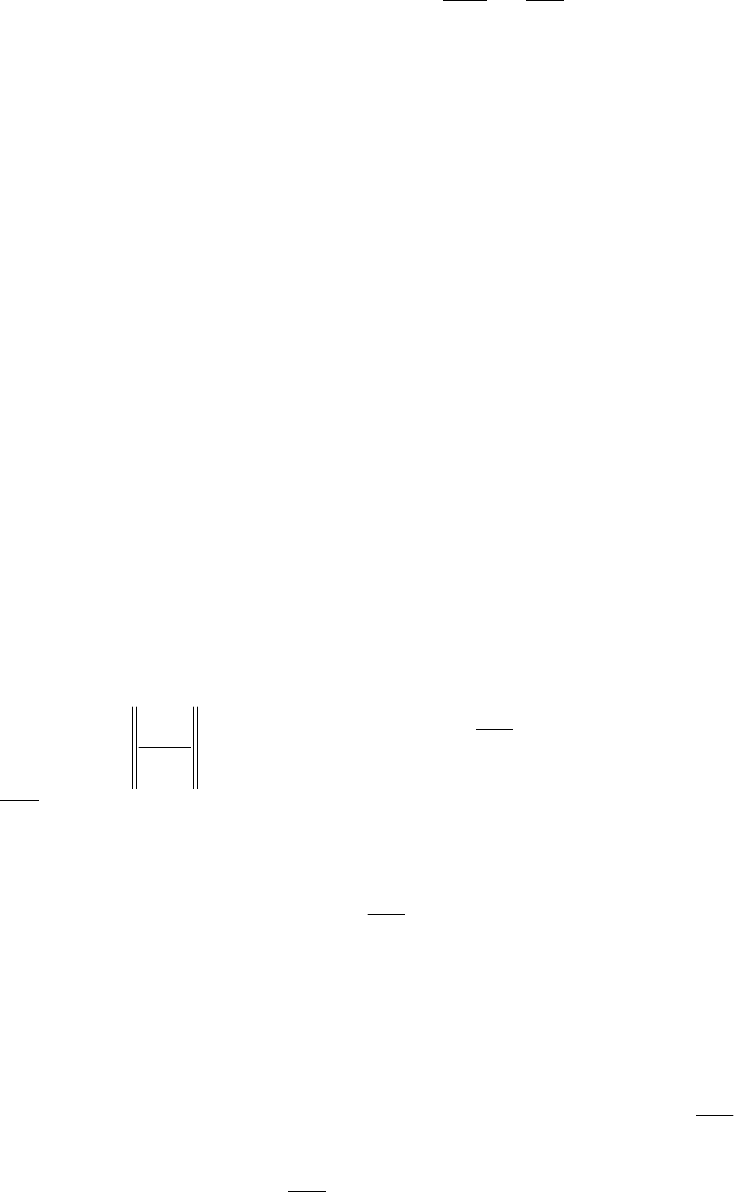
71
Из определения живучести оценок следует, что оценка более каче-
ственна, если она обеспечивает больший уровень живучести. При рас-
ширении комплекса условий
(),Ak
где (
,1,,1,),
ij i
ki mj n
=
=
т. е. каждое
условие
1
, ...,
m
A
A имеет дополнительно
i
n условий, под r понимается
вектор с компонентами
12
, , ...,
m
rr r.
Отметим, что оценка метода наименьших квадратов не обладает
свойством живучести, для нее условия (2.5.8), (5.2.9) не выполняются.
В качестве примеров рассмотрим наиболее важные критерии ус-
тойчивости оценок параметров интегрированных систем моделей при
нарушении стандартных условий нормального функционирования сис-
темы. Покажем связь традиционных критериев устойчивости с рассмот-
ренными выше критериями.
Пример 1
Устойчивость к малым изменениям в исходных данных. Этот,
наиболее часто используемый при исследовании систем обработки дан-
ных, критерий устойчивости фактически является третьим условием
корректно поставленной задачи по Адамару. Задача является корректно
поставленной, если достаточно малому изменению исходных данных
соответствует достаточно малое изменение решения.
Рассмотрим данный критерий на примере оценок метода наимень-
ших квадратов. В качестве меры устойчивости (
стабильности) традици-
онных оценок параметров линейных систем принимаются функции чув-
ствительности вида [14]
mj
y
jjj
T
oj
j
,1,/1)(
1
2
*
=λ==
∂
α∂
=Δ
−
WW
,
(5.2.12)
где
mj
j
,1, =λ
собственные числа матрицы планирования
T
WW. Кри-
терий устойчивости оценок характеризует их чувствительность к изме-
нению выхода объекта
1, 1,
j
j
m
Δ
<< ∀ = . (5.2.13)
В случае, когда хотя бы одно из собственных чисел λ
j
близко либо
равно нулю ()
j
Δ→∞, матрица WW
T
вырожденная, и оценки становят-
ся неустойчивыми. Причиной потери устойчивости в данном случае яв-
ляется нарушение шестого (
6
A
) условия нормального функционирова-
ние системы. С другой стороны, функции чувствительности
,1,
j
j
mΔ=
(5.2.12) связаны с относительной ошибкой аппроксимации оценок мето-
да наименьших квадратов
*
0
δα ,1,
j
j
m
=
(5.1.7) соотношениями

72
mj
j
j
,1,
σ
δα
2
*
0
==Δ
ξ
.
(5.2.14)
Малость величины
j
Δ фактически означает достаточно хорошую
точность оценок и указывает на связь критерия устойчивости оценок
(5.2.13) с критерием условной относительной эффективности (5.2.1).
В данном случае для оценок метода наименьших квадратов соответст-
вующий критерий устойчивости (5.2.2), можно представить в виде:
∞<<
λ
λ
=
δ
δ
=
∑
∑
=
=
C
A
A
е
m
j
j
m
j
j
0
1
1
0
*
0
*
0
*
0
/)
1
(
)(/)
1
(
/)(
)(/)(
)0,,(
kA
Aα
kα
kα
(5.2.15)
Критерий устойчивости (5.2.15) в отличие от классического критерия
(5.2.13) показывает не только потерю устойчивости при нарушении усло-
вий нормального функционирования системы, но и при конечных значе-
ниях C дает количественную оценку степени потери точности в C раз.
Например, при нарушении пятого условия нормального функцио-
нирования системы
5
()
A
A=k
, величина
1
5
1
λ
/
m
j
j
A
=
⎛⎞
⎜⎟
⎜⎟
⎝⎠
→∞
∑
, что приводит
к неустойчивости оценок метода наименьших квадратов.
Для оценок параметров интегрированных систем моделей наруше-
ние пятого условия нормального функционирования системы не приво-
дит к потере их устойчивости в силу ограниченности числителя крите-
рия (5.2.15). Например, для ортонормированной интегрированной сис-
темы моделей вида (5.1.4) среднеквадратическая ошибка аппроксима-
ции оценки параметров ограничена
5
*
/)( AKαδ
=
∞<<
+λ
ε+σ+σλ
∑
=
ηξ
C
K
K
m
j
jj
jjj
1
2
2222
)(
)(
(5.2.16)
при равенстве нулю всех собственных значений матрицы планирования
WW
T
( 0, 1,
j
j
m
λ
==).
Пример 2
Устойчивость к объему исходных данных. Данный критерий явля-
ется, по существу, вторым условием корректно поставленной задачи по
Адамару. Применительно к задаче оценки параметров линейных систем
вида
*
=+yFα
ξ
, второе условие корректно поставленной задачи требует
единственности решения систем линейных уравнений порядка m
TT*
()
yy
=
FWFα FWy (5.2.17)

73
относительно вектора параметров
),...,,(
21 m
α
α
α
=
α
. Необходимым ус-
ловием является выполнение неравенства
mn
≤
, (5.2.18)
где число оцениваемых параметров m должно быть больше либо равно
объему измерений выхода объекта
n. Условие (5.2.18) совпадает с усло-
вием необходимого объема исходной информации
6
A
для нормального
функционирования системы. В этой связи по аналогии с (5.2.15) имеет
место соответствующий критерий устойчивости решения системы ли-
нейных уравнений (5.2.17)
*
*
06
8
*
00
()/
(,,0) .
()/
A
е C
δ
δ
=
≤<∞
α
α k
α A
(5.2.19)
Пример 3
Устойчивость к действию случайных факторов. Отметим, что
ущерб от действия случайных факторов в моделях объекта и моделях
объектов-аналогов при выполнении четырех первых условий нормаль-
ного функционирования системы, приведенных в предыдущем парагра-
фе, может не приводить к таким последствиям, как отказ программы
либо устройства, где реализован алгоритм оценки параметров.
Это связано
с тем, что действия случайных факторов могут быть в
принципе контролируемыми. Например, путем предварительного про-
смотра измеренных значений входных и выходной величины объекта,
дополнительных априорных данных с целью отбраковки резко выде-
ляющихся значений – выбросов.
Наоборот, при невыполнении пятого и шестого условий нормаль-
ного функционирования системы незамедлительно наступает отказ про-
граммы
либо устройства, и причины этого отказа достаточно трудно
проконтролировать, хотя они могут быть связаны и с незначительным
действием случайных факторов.
С учетов сделанных замечаний, в качестве критерия устойчивости
оценок к действию случайных факторов может быть использована ве-
личина условной относительной точности в форме (5.2.4):
*
**
0
*
0
0
(δ )/ ( )
((), ,,0)
(δ )/
е KC
=
≤<∞
α Ak
ααk
α A
, (5.2.20)
где
*
(δ )/ ( )α Ak условная относительная ошибка аппроксимации оценок
параметров интегрированных систем моделей для вектора
*
δα в экстре-
мальных условиях
6
12
12 6
() ( , , , )
k
kk
A
AA=Ak . Удобно ввести логические
операции k
1
∪k
2
∪k
3
∪k
5
= 1 и k
6
∩k
7
= 0 (символ ∪ означает логическое

74
«или», а символ ∩ – логическое «и»), что соответствует выполнению ус-
ловий А
6
, А
7
и невыполнению хотя бы одного из условий А
1
, А
2
, А
3
, А
5
.
Условная относительная ошибка аппроксимации оценок метода
наименьших квадратов
0
*
0
/)( Aαδ
используется здесь в качестве «этало-
на точности». Нарушение условий А
1
, А
2
, А
3
, А
5
, связанные с действием
случайных факторов (при предварительном отсеве выбросов), не должно
приводить к значительному росту константы C. В этом случае критерий
(5.2.20) характеризует меру точности оценки
α
*
в экстремальных услови-
ях ()
Ak относительно уровня точности оценки метода наименьших квад-
ратов в условиях нормального функционирования модели объекта.
Например, для оценок параметров линейной ортонормированной
интегрированной системы моделей (5.1.4) критерий устойчивости (от-
носительной точности) оценок примет вид:
*
**
0
*
0
2222
η
ξ
2
1
0
1
0
(δ )/ ( )
((), ,,0)
(δ )/
λσ (σε)
()/()
(λ )
.
1
()/
λ
m
jj j
j
jj
m
j
j
е K
K
K
C
A
=
=
==
++
+
=
≤<∞
∑
∑
α Ak
ααk
α A
Ak
(5.2.21)
5.3. Вопросы оптимизации интегрированных систем идентификации
Оптимизация интегрированных систем идентификации связана с выбо-
ром управляющих параметров, определением вида модели исследуемых
объектов и вида моделей объектов-аналогов, представляющих дополни-
тельные априорные данные. Сложность данных задач заключается в
том, что они должны быть решены при ограниченных объемах исход-
ных и дополнительных данных.
При ограниченных выборках задача оптимизации интегрированных
систем
идентификации сводится к задачам параметрической и струк-
турной оптимизации интегрированных систем моделей по данным на-
блюдений входных и выходных переменных исследуемого объекта.
Остановимся на задаче параметрической оптимизации и методах
выбора управляющих параметров.
1. Определение управляющих параметров при наличии априор-
ной информации об ошибках измерения выхода объекта.
При корре-
ляционной матрице ошибок измерения выхода объекта вида
IW
2
σ
ξξ
=
,
где
2
σ
ξ
– дисперсия помех, а I – единичная матрица, одним из распро-
страненных методов определения управляющего параметра является
метод невязки.
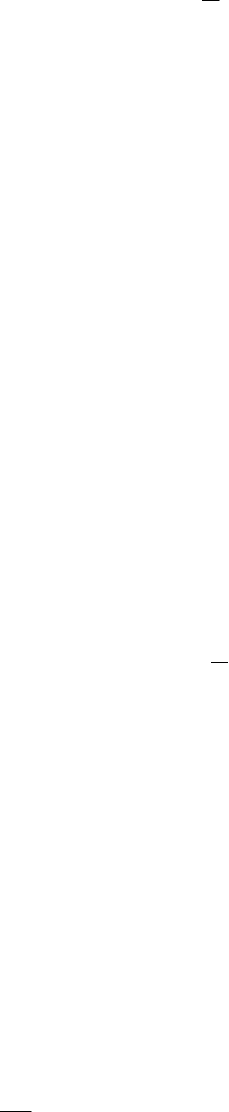
75
Суть данного метода заключалась в выборе такой оценки
*
β вектора
управляющего параметра, при котором выполнялось равенство
()
2
*2
1
1
() ( , ()) σ
n
ii
i
Jyf
n
=
=− =
∑
ξ
β x αβ , (5.3.1)
где
*
(, ())f x αβ модель исследуемого объекта,
*
()αβ – оценка параметров
интегрированной системы моделей.
Метод невязки распространяется и на случай коррелированных
ошибок измерения выхода объекта. Здесь функционал ()J
β (5.3.1) за-
меняется квадратичной формой
T1
ξ
−
eW e,
где
()
** *
11 2 2 11
(,(), (,(), , (,()
T
T
yf y f yf=− − −exαβ x αβ x αβ… – вектор не-
вязки,
1−
ξ
W
– обратная корреляционная матрица ошибок измерений вы-
хода объекта.
Тогда по аналогии с (5.3.1)
.1)(
1T
==
−
ξ
eWeβJ
(5.3.2)
Использование методов невязки (5.3.1), (5.3.2) приводит к смещен-
ным значениям управляющих параметров относительно оптимальных,
доставляющих минимум функционалу
()
,)(,(),(
1
)(
1
2
*0
∑
=
−=β
n
i
ii
ff
n
J βαxαx
(5.3.3)
эмпирической среднеквадратической ошибки аппроксимации исследуе-
мой модели объекта (, )
f
x α . Для устранения смещения вместо метода
невязки используют модифицированный метод невязки
,0,σ)(
2
>ΔΔ−=β
ξ
J
(5.3.4)
где Δ рекомендуется выбирать из интервала
22
ξξ
(0, 05σ 0, 3σ )−
.
2. Определение управляющих параметров при отсутствии ап-
риорной информации об ошибках измерения выхода объекта.
На
практике довольно часто информация о корреляционной матрице оши-
бок измерения выхода объекта
ξ
W
отсутствует. В этой связи для управ-
ляющего параметра используют прием разбиения исходной выборки
,, 1,
ii
yin=x
на два подмножества по n
1
и n
2
чисел [25]. Обучающее под-
множество yiP
ii
n
,,x ∈
1
δ
используем для построения оценки параметров

76
*
(αβ) , контрольное подмножество
2
δ
,,
ii
n
yiP
∈
x
используется для фор-
мирования эмпирического функционала
(
)
,),()(
2
2
*
∑
δ
∈
δ
−=
n
Pi
ii
fyJ )(βαxβ
(5.3.5)
где
12
δδ
,
nn
PP – подмножества множества P – целых чисел от 1 до n;
δ – номер способа разбиения исходной выборки на два подмножества,
δ=1, c .
В зависимости от числа наблюдений n
1
, n
2
обучающего и контроль-
ного подмножеств и способа разбиения выборки получаем различные
функционалы.
Для решения допустимых способов формирования обучающего и
контрольного подмножеств, представим функционал (5.3.5) в виде
δ
2
02
δ 1
() () ξ ,
n
c
i
iP
JJ d
=
∈
=+ +
∑∑
ββ
(5.3.6)
где
()
,,,)()(
1
2
*0
21
∑∑ ∑
=δ
∈∈
δδ
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
θ−=
c
PiPj
jjii
nn
yfJ βxxxβ
()
∑∑ ∑
=δ
∈∈
δδ
ξ
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
ξ+θ−=
c
Pi
i
Pj
jjjii
nn
fzd
1
21
))((,,)( xβxxx
,
()
i
f
x – значение восстанавливаемой зависимости в точке
2
δ
,
i
n
iP∈x ,
,1,
i
in=x ,
()
δ
1
*
θ ,,
n
ij j
jP
y
∈
∑
xx β – оценка ()
i
f
x .
Из (5.3.6) следует, что при
IW
2
σ
ξξ
=
0,
M
d
=
(5.3.7)
значения вектора управляющего параметра β, доставляющие минимум
функционалу M J(β), совпадают с соответствующим оптимальным
управляющим вектором, доставляющим минимум функционалу M J(β),
где М – символ математического ожидания.
Равенство (5.3.7) накладывает ограничения на формирование
обучающего и контрольного подмножеств и выполняется, когда зна-
чение индекса i из подмножества P
n
2
δ
не совпадает со значениями
cPj
n
,1,
1
=δ∈
δ
. Например, условию (5.3.7) соответствует функционал
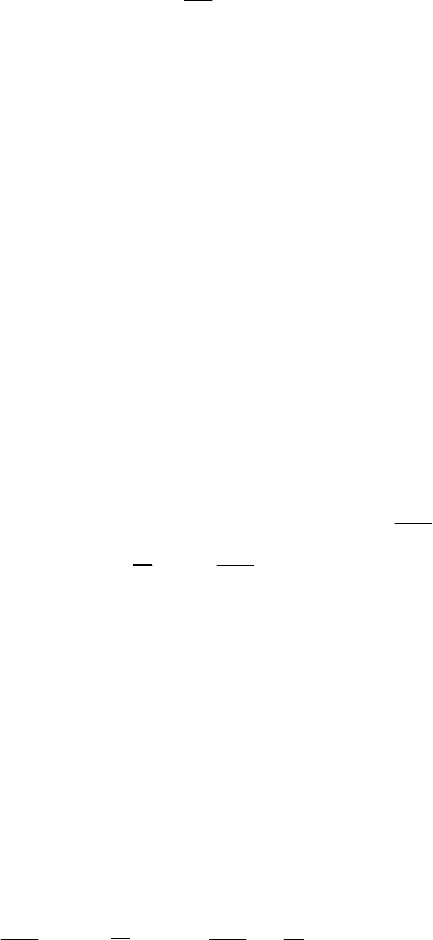
77
()
2
*
1, 3, 5, 2, 4, 6,
() θ ,, ,
iijj
ij
Jyxxy
==
⎛⎞
⎜⎟
⎜⎟
⎝⎠
=−
∑∑
ββ
……
(5.3.8)
в котором исходная выборка разбивается на две части чередования че-
рез одно наблюдение. Другим примером является функционал метода
«скользящий контроль» (“cross validation”)
()
2
**
1
() θ ,,
n
iijj
iji
Jyxxy
=≠
⎛⎞
⎜⎟
⎜⎟
⎝⎠
=−
∑∑
ββ, (5.3.9)
в котором обучающая последовательность формируется путем последо-
вательного удаления из выборки
nixy
ii
,1,, = одного наблюдения.
В конечном итоге задача параметрической оптимизации по определе-
нию вектора управляющих параметров сводится к определению корней
нелинейных уравнений (в случае использования методов невязки) либо
поиску минимума функции многих переменных при использовании
функционала (5.3.8) либо (5.3.9).
Для решения соответствующих оптимизационных задач могут быть
использованы различные методы, приведенные в приложении 2. Наибо-
лее
простыми являются методы без вычисления производных (метод
деления отрезка пополам, метод золотого сечения, деформируемого
многогранника и другие).
Задача структурной оптимизации заключается в определении вида
модели исследуемого объекта и вида модели объекта-аналога, которые
воспроизводят ранее полученные исходные и дополнительные априор-
ные данные и обеспечивают возможность их прогнозирования.
Данную задачу обычно решают
следующим образом. Составляется
набор возможных моделей исследуемого объекта
1
,1,
i
f
im
=
и возмож-
ных моделей объектов-аналогов
2
,1,
j
f
jm= , исходя из физической
сущности задачи и имеющейся информации.
Для сформированной структуры интегрированной системы моде-
лей, выбранных критериев качества решают задачу параметрической
оптимизации.
При неудовлетворительном воспроизведении исходных и дополни-
тельных априорных данных либо неудовлетворительном их прогнозе
осуществляется переход к другой интегрированной системе моделей и
задаче параметрической идентификации.
В результате получаем
последовательность адаптированных интег-
рированных систем моделей
*
*
12
,1, , , 1,
i
j
f
imFf jmF=∈ =∈ (5.3.10)
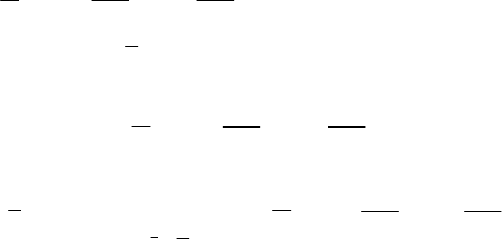
78
и последовательность соответствующих значений критериев качества
моделей
*
*
12
(, , 1,, 1, )
i
j
f
fimjmΦ==. Оптимальной считается та интег-
рированная система
00
,
f
f моделей, для которой критерии качества
достигают области заданных (проектных) значений Δ
*
*
12
(, , 1,, 1, )
i
j
ff i mj mΦ==∈Δ (5.3.11)
либо обеспечивают минимальную возможную ошибку
**
*
00 *
12
,
,argmin((,,1,,1,).
i
j
fFfF
f
fffimjm
∈∈
=Φ== (5.3.12)
Следует отметить, что ряд задач идентификации, в широком смыс-
ле, по определению информативных переменных, степени полиномов,
количества ортогональных функций в моделях объекта и моделях
объектов-аналогов сводится к задаче структурной оптимизации вида
(5.3.10)–(5.3.12).
79
Часть2
ПРИМЕРЫ ПРАКТИЧЕСКОГО ПРИМЕНЕНИЯ
И ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ
ИНТЕГРИРОВАННЫХ СИСТЕМ ИДЕНТИФИКАЦИИ
Глава 6
ПРИМЕРЫ РЕШЕНИЯ НАУЧНО-ТЕХНИЧЕСКИХ ЗАДАЧ
6.1. Прогноз добычи нефти и оценка извлекаемых запасов
1. Введение. В данном разделе рассматривается задача прогноза
добычи нефти и оценки извлекаемых запасов на основе интегрирован-
ных систем моделей, учитывающих дополнительную априорную ин-
формацию. Приводится алгоритм решения задачи адаптации интегриро-
ванных моделей с использованием данных истории разработки место-
рождения.
В качестве моделей добычи нефти на всех четырех стадиях разра-
ботки
месторождения часто используются нелинейные, заданные с точ-
ностью до параметров, функции вида:
()
36
2
5
2
αα
α
5
11 21
αα
3134
(, ) α ,(,) (,)α ,
(, ) α / αα .
t
t
ft e t f t ft e
ft t t
−
⋅
−
==⋅⋅
=+
ααα
α
(6.1.1)
Задача идентификации заключается в определении вида модели и
оценке вектора неизвестных параметров α на основе исходных и допол-
нительных априорных данных, полученных в процессе разработки ме-
сторождения.
Исходными данными, полученными в процессе разработки место-
рождения, являются:
1) технологические параметры разработки (дебиты добывающих и
приемистость нагнетательных скважин, обводненность продукции, за
-
бойные и пластовые давления, количество вводимых в эксплуатацию
скважин и т. д.);
2) фильтрационно-емкостные параметры пласта и скважины (про-
ницаемость, пъезопроводность, гидропроводность, скин-фактор и т. д.),
полученные на основе результатов геофизических и гидродинамических
исследований скважин.
В качестве дополнительных априорных сведений часто использу-
ются:
1) экспертные оценки об извлекаемых запасах
нефти;
80
2) прогнозные значения добычи нефти, полученные на основе раз-
личных методик их расчета, включая результаты геологического и гид-
родинамического моделирования;
3) различные экспертные оценки параметров моделей добычи неф-
ти, потенциальных дебитов скважин и т. д.
2. Прогноз добычи нефти с учетом априорной информации об
извлекаемых запасах. Рассмотрим методику проектирования алгорит-
мов прогноза
добычи с учетом априорной информации об извлекаемых
запасах на основе нелинейной интегрированной системы моделей вида:
*
0
(,
(τ,)dτ () ,
T
fs
⎧
⎪
⎪
⎨
⎪
⎪
⎩
=+
=+=+
∫
qfα) ξ
s αηαη
(6.1.2)
где
*
12
((),( ),...,( ))
T
n
qt qt qt=q – вектор столбец фактических значений на-
копленной добычи нефти
)(
i
tq за соответствующие промежутки време-
ни
1
,1,
i
i
ttt i n
−
Δ= − =
(год, месяц);
12
( ( , ), ( , ), ..., ( , )
T
n
(ftft ft
=
f α) αα α–
вектор столбец значений накопленной за соответствующий промежуток
времени добычи нефти, полученной на основе модели (, )
f
t α (6.1.1);
12
(, ,..., )
T
l
s
ss=s
– вектор экспертных оценок извлекаемых запасов нефти
за время разработки месторождения
Т, полученных на основе различ-
ных методик их расчета;
12
(α , α ,...., α )
m
=
α – вектор неизвестных пара-
метров,
,
ξ
η
– вектора случайные величины, представляющие ошибки
измерений дебита нефти и ошибки расчетов извлекаемых запасов.
Основываясь на изложенных в третьей главе результатах, в качест-
ве оптимальных оценок параметров модели добычи нефти (, )
f
t α и оп-
тимальных значений управляющих параметров будем использовать
приближение вида:
*
1
2
***
() argmin( β ),
arg min( ( ( )) ,
l
kk
k =
==+
=−
∑
α
β
αβ Φ JQ
β qfαβ
(6.1.3)
где Ф – комбинированный критерий качества;
2
*
()
()
Wy
=−Jqfα
и
2
()
()
kk
ws
ss=−Q α – частные квадратичные критерии качества модели
добычи нефти и, соответственно, модели извлекаемых запасов нефти;
β ,1,
k
kl= – управляющие параметры, определяющие вес дополнитель-
ных априорных данных об извлекаемых запасах
12
(, ,..., )
T
l
s
ss=s ;
*** *
12
(β , β , ..., β )
k
=β – оптимальные значения управляющих параметров;
X – норма вектора Х.
