Stewart J. Calculus

We sometimes read that the inventors of calculus were Sir Isaac Newton (1642–1727) and

Gottfried Wilhelm Leibniz (1646–1716). But we know that the basic ideas behind integration

were investigated 2500 years ago by ancient Greeks such as Eudoxus and Archimedes, and

methods for ﬁnding tangents were pioneered by Pierre Fermat (1601–1665), Isaac Barrow

(1630–1677), and others. Barrow––who taught at Cambridge and was a major inﬂuence on

Newton––was the ﬁrst to understand the inverse relationship between differentiation and integra-

tion. What Newton and Leibniz did was to use this relationship, in the form of the Fundamental

Theorem of Calculus, in order to develop calculus into a systematic mathematical discipline. It

is in this sense that Newton and Leibniz are credited with the invention of calculus.

Read about the contributions of these men in one or more of the given references and write a

report on one of the following three topics. You can include biographical details, but the main

thrust of your report should be a description, in some detail, of their methods and notations. In

particular, you should consult one of the sourcebooks, which give excerpts from the original

publications of Newton and Leibniz, translated from Latin to English.

N

The Role of Newton in the Development of Calculus

N

The Role of Leibniz in the Development of Calculus

N

The Controversy between the Followers of Newton and Leibniz over

Priority in the Invention of Calculus

References

1. Carl Boyer and Uta Merzbach, A History of Mathematics (New York: Wiley, 1987),

Chapter 19.

NEWTON, LEIBNIZ, AND THE INVENTION OF C ALCULUS

W R I T I N G

P R O J E C T

The following exercises are intended only for those who have

already covered Chapter 7.

67– 71 Evaluate the integral.

67. 68.

69. 70.

71.

The area labeled is three times the area labeled . Express

in terms of .

0

y

x

a

A

y=´

0

y

x

b

B

y=´

ab

AB

72.

y

1+

s

3

0

t

2

! 1

t

4

! 1

dt

y

2

1

$x ! 1%

3

x

2

dx

y

)

x

2

" 1 "

1

x

2

" 1

*

dx

y

10

!10

2e

x

sinh x " cosh x

dx

y

$sin x " sinh x% dx

bottom of the households? Find the coefﬁcient of

inequality.

;

66. On May 7, 1992, the space shuttle Endeavour was launched

on mission STS-49, the purpose of which was to install a new

perigee kick motor in an Intelsat communications satellite.

The table gives the velocity data for the shuttle between

liftoff and the jettisoning of the solid rocket boosters.

(a) Use a graphing calculator or computer to model these

data by a third-degree polynomial.

(b) Use the model in part (a) to estimate the height reached

by the Endeavour, 125 seconds after liftoff.

50%

332

|| ||

CHAPTER 5 INTEGRALS

Event Time (s) Velocity (ft+s)

Launch 0 0

Begin roll maneuver 10 185

End roll maneuver 15 319

Throttle to 89% 20 447

Throttle to 67% 32 742

Throttle to 104% 59 1325

Maximum dynamic pressure 62 1445

Solid rocket booster separation 125 4151

SECTION 5.5 THE SUBSTITUTION RULE

|| ||

333

2. Carl Boyer, The History of the Calculus and Its Conceptual Development (New York: Dover,

1959), Chapter V.

3. C. H. Edwards, The Historical Development of the Calculus (New York: Springer-Verlag,

1979), Chapters 8 and 9.

4. Howard Eves, An Introduction to the History of Mathematics, 6th ed. (New York: Saunders,

1990), Chapter 11.

5. C. C. Gillispie, ed., Dictionary of Scientiﬁc Biography (New York: Scribner’s, 1974).

See the article on Leibniz by Joseph Hofmann in Volume VIII and the article on Newton by

I. B. Cohen in Volume X.

6. Victor Katz, A History of Mathematics: An Introduction (New York: HarperCollins, 1993),

Chapter 12.

7. Morris Kline, Mathematical Thought from Ancient to Modern Times (New York: Oxford

University Press, 1972), Chapter 17.

Sourcebooks

1. John Fauvel and Jeremy Gray, eds., The History of Mathematics: A Reader (London:

MacMillan Press, 1987), Chapters 12 and 13.

2. D. E. Smith, ed., A Sourcebook in Mathematics (New York: Dover, 1959), Chapter V.

3. D. J. Struik, ed., A Sourcebook in Mathematics, 1200–1800 (Princeton, N.J.: Princeton

University Press, 1969), Chapter V.

THE SUBSTITUTION RULE

Because of the Fundamental Theorem, it’s important to be able to ﬁnd antiderivatives. But

our antidifferentiation formulas don’t tell us how to evaluate integrals such as

To ﬁnd this integral we use the problem-solving strategy of introducing something extra.

Here the “something extra” is a new variable; we change from the variable x to a new vari-

able u. Suppose that we let be the quantity under the root sign in (1), . Then

the differential of is . Notice that if the in the notation for an integral were

to be interpreted as a differential, then the differential would occur in (1) and so,

formally, without justifying our calculation, we could write

But now we can check that we have the correct answer by using the Chain Rule to differ-

entiate the ﬁnal function of Equation 2:

In general, this method works whenever we have an integral that we can write in the

form . Observe that if , then

y

F%$t$x%% t%$x% dx ! F$t$x%% " C

3

F% ! fx f $t$x%% t%$x% dx

d

dx

[

2

3

$x

2

" 1%

3+2

" C

]

!

2

3

!

3

2

$x

2

" 1%

1+2

! 2x ! 2x

s

x

2

" 1

!

2

3

u

3+2

" C !

2

3

$x

2

" 1%

3+2

" C

y

2x

s

1 " x

2

dx !

y

s

1 " x

2

2x dx !

y

s

u

du

2

2x dx

dxdu ! 2x dxu

u ! 1 " x

2

u

y

2x

s

1 " x

2

dx

1

5.5

N

Differentials were deﬁned in Section 3.9.

If , then

du ! f %$x% dx

u ! f $x%

because, by the Chain Rule,

If we make the “change of variable” or “substitution” , then from Equation 3

we have

or, writing , we get

Thus we have proved the following rule.

THE SUBSTITUTION RULE If is a differentiable function whose range

is an interval and is continuous on , then

Notice that the Substitution Rule for integration was proved using the Chain Rule for

differentiation. Notice also that if , then , so a way to remember the

Substitution Rule is to think of and in (4) as differentials.

Thus the Substitution Rule says: It is permissible to operate with dx and du after

integral signs as if they were differentials.

EXAMPLE 1 Find .

SOLUTION We make the substitution because its differential is ,

which, apart from the constant factor 4, occurs in the integral. Thus, using

and the Substitution Rule, we have

Notice that at the ﬁnal stage we had to return to the original variable .

M

The idea behind the Substitution Rule is to replace a relatively complicated integral

by a simpler integral. This is accomplished by changing from the original variable to

a new variable that is a function of . Thus, in Example 1, we replaced the integral

by the simpler integral .

The main challenge in using the Substitution Rule is to think of an appropriate substi-

tution. You should try to choose to be some function in the integrand whose differential

also occurs (except for a constant factor). This was the case in Example 1. If that is not

u

1

4

x cos u dux x

3

cos$x

4

" 2% dx

xu

x

!

1

4

sin$x

4

" 2% " C

!

1

4

sin u " C

y

x

3

cos$x

4

" 2% dx !

y

cos u !

1

4

du !

1

4

y

cos u du

x

3

dx ! du+4

du ! 4x

3

dxu ! x

4

" 2

y

x

3

cos$x

4

" 2% dx

dudx

du ! t%$x% dxu ! t$x%

y

f $t$x%% t%$x% dx !

y

f $u% du

IfI

u ! t$x%

4

y

f $t$x%% t%$x% dx !

y

f $u% du

F% ! f

y

F%$t$x%% t%$x% dx ! F$t$x%% " C ! F$u% " C !

y

F%$u% du

u ! t$x%

d

dx

'F$t$x%%( ! F%$t$x%%t%$x%

334

|| ||

CHAPTER 5 INTEGRALS

N Check the answer by differentiating it.

SECTION 5.5 THE SUBSTITUTION RULE

|| ||

335

possible, try choosing to be some complicated part of the integrand (perhaps the inner

function in a composite function). Finding the right substitution is a bit of an art. It’s not

unusual to guess wrong; if your ﬁrst guess doesn’t work, try another substitution.

EXAMPLE 2 Evaluate .

SOLUTION 1 Let . Then , so . Thus the Substitution Rule

gives

SOLUTION 2 Another possible substitution is . Then

so

(Or observe that so .) Therefore

M

EXAMPLE 3 Find .

SOLUTION Let . Then , so and

M

The answer to Example 3 could be checked by differentiation, but instead let’s check

it with a graph. In Figure 1 we have used a computer to graph both the integrand

and its indeﬁnite integral (we take the case

). Notice that decreases when is negative, increases when is positive,

and has its minimum value when . So it seems reasonable, from the graphical evi-

dence, that is an antiderivative of .

EXAMPLE 4 Calculate .

SOLUTION If we let , then , so . Therefore

M

y

cos 5x dx !

1

5

y

cos u du !

1

5

sin u " C !

1

5

sin 5x " C

dx !

1

5

dudu ! 5 dxu ! 5x

y

cos 5x dx

ft

f $x% ! 0

f $x%f $x%t$x%C ! 0

t$x% ! !

1

4

s

1 ! 4x

2

f $x% ! x+

s

1 ! 4x

2

! !

1

8

(

2

s

u

)

" C ! !

1

4

s

1 ! 4x

2

" C

y

x

s

1 ! 4x

2

dx ! !

1

8

y

1

s

u

du ! !

1

8

y

u

!1+2

du

x dx ! !

1

8

dudu ! !8x dxu ! 1 ! 4x

2

y

x

s

1 ! 4x

2

dx

V

!

u

3

" C !

1

3

$2x " 1%

3+2

" C

y

s

2x " 1 dx !

y

u ! u du !

y

u

2

du

2u du ! 2 dxu

2

! 2x " 1,

dx !

s

2x " 1 du ! u dudu !

dx

s

2x " 1

u !

s

2x " 1

!

1

3

$2x " 1%

3+2

" C

!

1

2

!

u

3+2

" C !

1

3

u

3+2

" C

y

s

2x " 1 dx !

y

s

u

du

2

!

1

2

y

u

1+2

du

dx ! du+2du ! 2 dxu ! 2x " 1

y

s

2x " 1 dx

u

1

_1

_1 1

©=

-

ƒdx

f

F I G U R E 1

©=

j

ƒdx=_ œ„„„„„„

x

œ„„„„„„

1-4≈

1

4

ƒ=

EXAMPLE 5 Find .

SOLUTION An appropriate substitution becomes more obvious if we factor as . Let

. Then , so . Also , so :

M

DEFINITE INTEGRALS

When evaluating a deﬁnite integral by substitution, two methods are possible. One method

is to evaluate the indeﬁnite integral ﬁrst and then use the Fundamental Theorem. For

instance, using the result of Example 2, we have

Another method, which is usually preferable, is to change the limits of integration when

the variable is changed.

THE SUBSTITUTION RULE FOR DEFINITE INTEGRALS If is continuous on

and is continuous on the range of , then

PROOF Let be an antiderivative of . Then, by (3), is an antiderivative of

, so by Part 2 of the Fundamental Theorem, we have

But, applying FTC2 a second time, we also have

M

EXAMPLE 6 Evaluate using (5).

y

4

0

s

2x " 1 dx

V

y

t$b%

t$a%

f $u% du ! F$u%

]

t$a%

t$b%

! F$t$b%% ! F$t$a%%

y

b

a

f $t$x%% t%$x% dx ! F$t$x%%

]

b

a

! F$t$b%% ! F$t$a%%

f $t$x%% t%$x%

F$t$x%%fF

y

b

a

f $t$x%% t%$x% dx !

y

t$b%

t$a%

f $u% du

u ! t$x%f'a, b(

t%

5

!

1

3

$9%

3+2

!

1

3

$1%

3+2

!

1

3

$27 ! 1% !

26

3

y

4

0

s

2x " 1 dx !

y

s

2x " 1 dx

]

0

4

!

1

3

$2x " 1%

3+2

]

0

4

!

1

7

$1 " x

2

%

7+2

!

2

5

$1 " x

2

%

5+2

"

1

3

$1 " x

2

%

3+2

" C

!

1

2

(

2

7

u

7+2

! 2 '

2

5

u

5+2

"

2

3

u

3+2

)

" C

!

1

2

y

$u

5+2

! 2u

3+2

" u

1+2

% du

!

y

s

u

$u ! 1%

2

du

2

!

1

2

y

s

u

$u

2

! 2u " 1% du

y

s

1 " x

2

x

5

dx !

y

s

1 " x

2

x

4

' x dx

x

4

! $u ! 1%

2

x

2

! u ! 1x dx ! du+2du ! 2x dxu ! 1 " x

2

x

4

! xx

5

y

s

1 " x

2

x

5

dx

336

|| ||

CHAPTER 5 INTEGRALS

N This rule says that when using a substitution

in a deﬁnite integral, we must put everything in

terms of the new variable , not only and

but also the limits of integration. The new limits

of integration are the values of that correspond

to and .x ! bx ! a

u

dxxu

SOLUTION Using the substitution from Solution 1 of Example 2, we have and

. To ﬁnd the new limits of integration we note that

and

Therefore

Observe that when using (5) we do not return to the variable x after integrating. We

simply evaluate the expression in u between the appropriate values of u.

M

EXAMPLE 7 Evaluate .

SOLUTION Let . Then , so . When , and

when , . Thus

M

SYMMETRY

The next theorem uses the Substitution Rule for Deﬁnite Integrals (5) to simplify the cal-

culation of integrals of functions that possess symmetry properties.

INTEGRALS OF SYMMETRIC FUNCTIONS Suppose is continuous on .

(a) If is even , then .

(b) If is odd , then .

x

a

!a

f $x% dx ! 0' f $!x% ! !f $x%(f

x

a

!a

f $x% dx ! 2 x

a

0

f $x% dx' f $!x% ! f $x%(f

'!a, a(f

6

!

1

5

)

!

1

7

"

1

2

*

!

1

14

! !

1

5

"

!

1

u

#

!2

!7

!

1

5u

#

!2

!7

y

2

1

dx

$3 ! 5x%

2

! !

1

5

y

!7

!2

du

u

2

u ! !7x ! 2

u ! !2x ! 1dx ! !du+5du ! !5 dxu ! 3 ! 5x

y

2

1

dx

$3 ! 5x%

2

F I G U R E 2

y

x

0

1

2

3

4

y=œ

„„„„„

2x+1

y

u

0

1

2

3

91

œ„u

2

y=

!

1

3

$9

3+2

! 1

3+2

% !

26

3

!

1

2

!

2

3

u

3+2

]

1

9

y

4

0

s

2x " 1 dx !

y

9

1

2

s

u

du

when x ! 4, u ! 2$4% " 1 ! 9when x ! 0, u ! 2$0% " 1 ! 1

dx ! du+2

u ! 2x " 1

SECTION 5.5 THE SUBSTITUTION RULE

|| ||

337

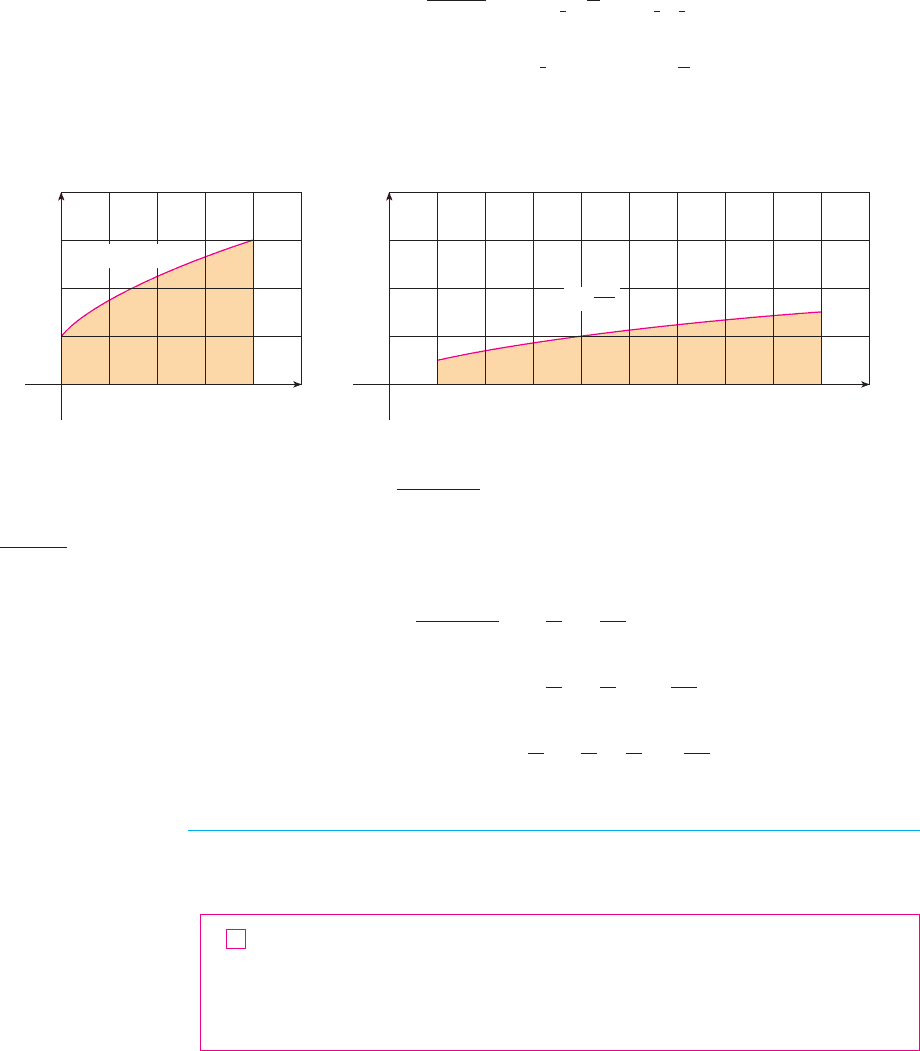
N The geometric interpretation of Example 6 is

shown in Figure 2. The substitution

stretches the interval by a factor of and

translates it to the right by unit. The Substitu-

tion Rule shows that the two areas are equal.

1

2'0, 4(

u ! 2x " 1

N The integral given in Example 7 is an

abbreviation for

y

2

1

$3 ! 5x%

2

dx

PROOF We split the integral in two:

In the ﬁrst integral on the far right side we make the substitution . Then

and when , . Therefore

and so Equation 7 becomes

(a) If is even, then so Equation 8 gives

(b) If is odd, then and so Equation 8 gives

M

Theorem 6 is illustrated by Figure 3. For the case where is positive and even, part (a)

says that the area under from to is twice the area from to because of

symmetry. Recall that an integral can be expressed as the area above the -axis

and below minus the area below the axis and above the curve. Thus part (b) says

the integral is because the areas cancel.

EXAMPLE 8 Since satisﬁes , it is even and so

M

EXAMPLE 9 Since satisﬁes , it is odd

and so

M

y

1

!1

tan x

1 " x

2

" x

4

dx ! 0

f !!x" ! !f !x"f !x" ! !tan x"#!1 " x

2

" x

4

"

! 2

[

1

7

x

7

" x

]

0

2

! 2

(

128

7

" 2

)

!

284

7

y

2

!2

!x

6

" 1" dx ! 2

y

2

0

!x

6

" 1" dx

f !!x" ! f !x"f !x" ! x

6

" 1

0

y ! f !x"

xx

b

a

f !x" dx

a0a!ay ! f !x"

f

y

a

!a

f !x" dx ! !

y

a

0

f !u" du "

y

a

0

f !x" dx ! 0

f !!u" ! !f !u"f

y

a

!a

f !x" dx !

y

a

0

f !u" du "

y

a

0

f !x" dx ! 2

y

a

0

f !x" dx

f !!u" ! f !u"f

y

a

!a

f !x" dx !

y

a

0

f !!u" du "

y

a

0

f !x" dx

8

!

y

!a

0

f !x" dx ! !

y

a

0

f !!u"!!du" !

y

a

0

f !!u" du

u ! ax ! !adu ! !dx

u ! !x

y

a

!a

f !x" dx !

y

0

!a

f !x" dx "

y

a

0

f !x" dx ! !

y

!a

0

f !x" dx "

y

a

0

f !x" dx

7

338

|| ||

CHAPTER 5 INTEGRALS

0

y

x

_a

a

F I G U R E 3

(a)

ƒ even,

j

 ƒ dx=2

j

ƒ dx

0

a

_a

a

0

x

_a

a

y

(b)

ƒ odd,

j

 ƒ dx=0

_a

a

4.

y

dt

!1 ! 6t"

4

, u ! 1 ! 6t

y

x

2

s

x

3

" 1 dx, u ! x

3

" 1

3.

1–6 Evaluate the integral by making the given substitution.

1.

2.

y

x

3

!2 " x

4

"

5

dx, u ! 2 " x

4

y

cos 3x dx, u ! 3x

E X E R C I S E S

5.5

SECTION 5.5 THE SUBSTITUTION RULE

|| ||

339

37. 38.

39. 40.

41. 42.

43. 44.

45.

47. 48.

49. 50.

;

51–52 Use a graph to give a rough estimate of the area of the

region that lies under the given curve. Then ﬁnd the exact area.

51. ,

52. ,

53. Evaluate by writing it as a sum of

two integrals and interpreting one of those integrals in terms

of an area.

54. Evaluate by making a substitution and inter-

preting the resulting integral in terms of an area.

55. Breathing is cyclic and a full respiratory cycle from the

beginning of inhalation to the end of exhalation takes about 5 s.

The maximum rate of air ﬂow into the lungs is about 0.5 L#s.

This explains, in part, why the function

has often been used to model the rate of air ﬂow into the

lungs. Use this model to ﬁnd the volume of inhaled air in the

lungs at time .

56. A model for the basal metabolism rate, in , of a young

man is , where is the time in

hours measured from 5:00

AM. What is the total basal metab-

olism of this man, , over a 24-hour time period?

If is continuous and , ﬁnd .

58. If is continuous and , ﬁnd .

y

3

0

xf !x

2

" dx

y

9

0

f !x" dx ! 4f

y

2

0

f !2x" dx

y

4

0

f !x" dx ! 10f

57.

x

24

0

R!t" dt

tR!t" ! 85 ! 0.18 cos!

#

t#12"

kcal#h

t

f !t" !

1

2

sin!2

#

t#5"

x

1

0

x

s

1 ! x

4

dx

x

2

!2

!x " 3"

s

4 ! x

2

dx

0 $ x $

#

y ! 2 sin x ! sin 2x

0 $ x $ 1

y !

s

2x " 1

y

T#2

0

sin!2

#

t#T !

%

"

dt

y

1

1#2

cos!x

!2

"

x

3

dx

y

4

0

x

s

1 " 2x

dx

y

2

1

x

s

x ! 1 dx

y

a

0

x

s

a

2

! x

2

dx

46.

y

a

0

x

s

x

2

" a

2

dx !a & 0"

y

#

#2

0

cos x sin!sin x" dx

y

13

0

dx

s

3

!1 " 2x"

2

y

#

#2

!

#

#2

x

2

sin x

1 " x

6

dx

y

#

#6

!

#

#6

tan

3

'

d

'

y

1#2

1#6

csc

#

t cot

#

t dt

y

#

0

sec

2

!t#4" dt

y

s

#

0

x cos!x

2

" dx

y

1

0

x

2

!1 " 2x

3

"

5

dx

5.

6.

7–30 Evaluate the indeﬁnite integral.

7. 8.

9. 10.

11. 12.

13. 14.

15. 16.

18.

19. 20.

21. 22.

24.

25. 26.

27. 28.

29. 30.

;

31–34 Evaluate the indeﬁnite integral. Illustrate and check that

your answer is reasonable by graphing both the function and its

antiderivative (take ).

31. 32.

33. 34.

35 –50 Evaluate the deﬁnite integral.

35. 36.

y

7

0

s

4 " 3x

dx

y

2

0

!x ! 1"

25

dx

y

tan

2

'

sec

2

'

d

'

y

sin

3

x cos x dx

y

sin

s

x

s

x

dx

y

x!x

2

! 1"

3

dx

C ! 0

y

x

3

s

x

2

" 1 dx

y

x

s

4

x " 2

dx

y

x

2

s

1 ! x

dx

y

cos x

sin

2

x

dx

y

sin t sec

2

!cos t" dt

y

sec

3

x tan x dx

y

dt

cos

2

t

s

1 " tan t

y

s

cot x

csc

2

x dx

23.

y

cos!

#

#x"

x

2

dx

y

z

2

s

3

1 " z

3

dz

y

!1 " tan

'

"

5

sec

2

'

d

'

y

cos

'

sin

6

'

d

'

y

s

x

sin!1 " x

3#2

" dx

y

cos

s

t

s

t

dt

17.

y

sec 2

'

tan 2

'

d

'

y

a " bx

2

s

3ax " bx

3

dx

y

1

!5t " 4"

2.7

dt

y

sin

#

t dt

y

x

!x

2

" 1"

2

dx

y

!x " 1"

s

2x " x

2

dx

y

!3t " 2"

2.4

dt

y

!3x ! 2"

20

dx

y

x

2

!x

3

" 5"

9

dx

y

x sin!x

2

" dx

y

sec

2

!1#x"

x

2

dx, u ! 1#x

y

cos

3

'

sin

'

d

'

, u ! cos

'

The following exercises are intended only for those who have

already covered Chapter 7.

65– 82 Evaluate the integral.

66.

68.

70.

71. 72.

74.

75. 76.

77. 78.

80.

81. 82.

83. Use Exercise 62 to evaluate the integral

y

#

0

x sin x

1 " cos

2

x

dx

y

1#2

0

sin

!1

x

s

1 ! x

2

dx

y

1

0

e

z

" 1

e

z

" z

dz

y

1

0

xe

!x

2

dx

y

e

4

e

dx

x

s

ln x

79.

y

x

1 " x

4

dx

y

cot x dx

y

sin x

1 " cos

2

x

dx

y

sin 2x

1 " cos

2

x

dx

y

sin!ln x"

x

dx

y

1 " x

2

dx

73.

y

tan

!1

x

1 " x

2

dx

y

e

tan x

sec

2

x dx

y

e

cos t

sin t dt

y

e

x

s

1 " e

x

dx

69.

y

dx

ax " b

!a " 0"

y

!ln x"

2

x

dx

67.

y

e

x

sin!e

x

" dx

y

dx

5 ! 3x

65.

59. If is continuous on , prove that

For the case where and , draw a diagram

to interpret this equation geometrically as an equality of areas.

60. If is continuous on , prove that

For the case where , draw a diagram to interpret this

equation geometrically as an equality of areas.

If and are positive numbers, show that

62. If is continuous on , use the substitution to

show that

63. If is continuous, prove that

64. Use Exercise 63 to evaluate and .

x

#

#2

0

sin

2

x dxx

#

#2

0

cos

2

x dx

y

#

#2

0

f !cos x" dx !

y

#

#2

0

f !sin x" dx

f

y

#

0

xf !sin x" dx !

#

2

y

#

0

f !sin x" dx

u !

#

! x$0,

#

%f

y

1

0

x

a

!1 ! x"

b

dx !

y

1

0

x

b

!1 ! x"

a

dx

ba

61.

f !x" ( 0

y

b

a

f !x " c" dx !

y

b"c

a"c

f !x" dx

!f

0

)

a

)

bf !x" ( 0

y

b

a

f !!x" dx !

y

!a

!b

f !x" dx

!f

340

|| ||

CHAPTER 5 INTEGRALS

REVIEW

C O N C E P T C H E C K

5

(b) If is the rate at which water ﬂows into a reservoir, what

does represent?

5. Suppose a particle moves back and forth along a straight line

with velocity , measured in feet per second, and accelera-

tion .

(a) What is the meaning of ?

(b) What is the meaning of ?

(c) What is the meaning of ?

6. (a) Explain the meaning of the indeﬁnite integral .

(b) What is the connection between the deﬁnite integral

and the indeﬁnite integral ?

7. Explain exactly what is meant by the statement that “differen-

tiation and integration are inverse processes.”

8. State the Substitution Rule. In practice, how do you use it?

x f !x" dxx

b

a

f !x" dx

x f !x" dx

x

120

60

a!t" dt

x

120

60

&

v!t"

&

dt

x

120

60

v!t" dt

a!t"

v!t"

x

t

2

t

1

r!t" dt

r!t"

1. (a) Write an expression for a Riemann sum of a function .

Explain the meaning of the notation that you use.

(b) If , what is the geometric interpretation of a

Riemann sum? Illustrate with a diagram.

(c) If takes on both positive and negative values, what is

the geometric interpretation of a Riemann sum? Illustrate

with a diagram.

2. (a) Write the deﬁnition of the deﬁnite integral of a function

from to .

(b) What is the geometric interpretation of if

?

(c) What is the geometric interpretation of if

takes on both positive and negative values? Illustrate with a

diagram.

3. State both parts of the Fundamental Theorem of Calculus.

4. (a) State the Net Change Theorem.

f !x"

x

b

a

f !x" dx

f !x" ( 0

x

b

a

f !x" dx

ba

f !x"

f !x" ( 0

f

Determine whether the statement is true or false. If it is true, explain why.

If it is false, explain why or give an example that disproves the statement.

1. If and are continuous on , then

2. If and are continuous on , then

3. If is continuous on , then

4. If is continuous on , then

5. If is continuous on and , then

6. If is continuous on , then .

y

3

1

f *!v" dv ! f !3" ! f !1"$1, 3%f *

y

b

a

s

f !x"

dx !

'

y

b

a

f !x" dx

f !x" ( 0$a, b%f

y

b

a

xf !x" dx ! x

y

b

a

f !x" dx

$a, b%f

y

b

a

5f !x" dx ! 5

y

b

a

f !x" dx

$a, b%f

y

b

a

$ f !x" t!x"% dx !

(y

b

a

f !x" dx

)(y

b

a

t!x" dx

)

$a, b%tf

y

b

a

$ f !x" " t!x"% dx !

y

b

a

f !x" dx "

y

b

a

t!x" dx

$a, b%tf

7. If and are continuous and for , then

8. If and are differentiable and for ,

then for .

9.

10.

11.

12.

represents the area under the curve

from 0 to 2.

13. All continuous functions have derivatives.

14. All continuous functions have antiderivatives.

15. If is continuous on , then

d

dx

(y

b

a

f !x" dx

)

! f !x"

$a, b%f

y ! x ! x

3

x

2

0

!x ! x

3

" dx

y

1

!2

1

x

4

dx ! !

3

8

y

5

!5

!ax

2

" bx " c" dx ! 2

y

5

0

!ax

2

" c" dx

y

1

!1

(

x

5

! 6x

9

"

sin x

!1 " x

4

"

2

)

dx ! 0

a

)

x

)

bf *!x" ( t*!x"

a

)

x

)

bf !x" ( t!x"tf

y

b

a

f !x" dx (

y

b

a

t!x" dx

a $ x $ bf !x" ( t!x"tf

T R U E - FA L S E Q U I Z

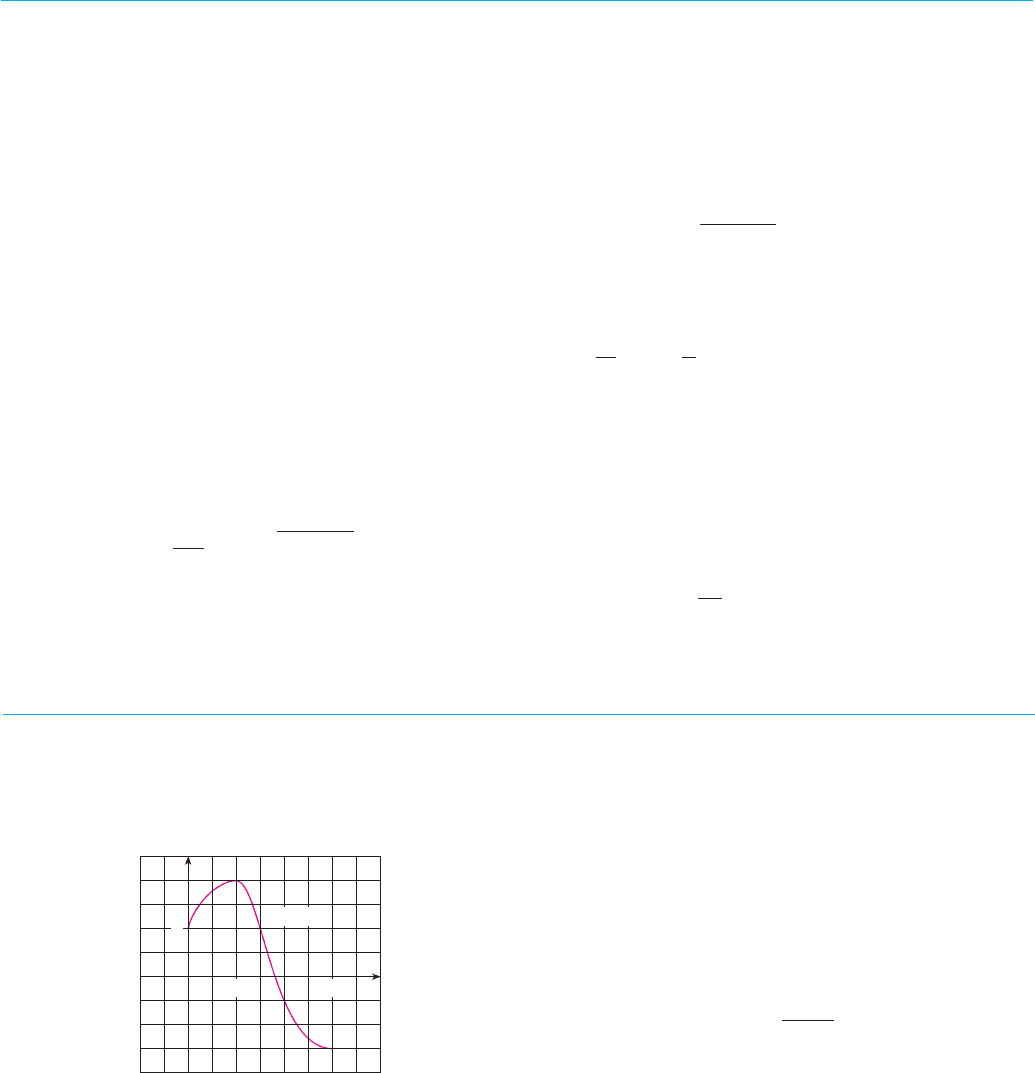
1. Use the given graph of to ﬁnd the Riemann sum with six

subintervals. Take the sample points to be (a) left endpoints and

(b) midpoints. In each case draw a diagram and explain what

the Riemann sum represents.

2. (a) Evaluate the Riemann sum for

with four subintervals, taking the sample points to be right

endpoints. Explain, with the aid of a diagram, what the

Riemann sum represents.

0 $ x $ 2f !x" ! x

2

! x

2

x

y

2

0

6

y=ƒ

f

(b) Use the deﬁnition of a deﬁnite integral (with right end-

points) to calculate the value of the integral

(c) Use the Fundamental Theorem to check your answer to

part (b).

(d) Draw a diagram to explain the geometric meaning of the

integral in part (b).

3. Evaluate

by interpreting it in terms of areas.

4. Express

as a deﬁnite integral on the interval and then evaluate

the integral.

$0,

#

%

lim

n

l

+

*

n

i!1

sin x

i

,x

y

1

0

(

x "

s

1 ! x

2

)

dx

y

2

0

!x

2

! x" dx

E X E R C I S E S

CHAPTER 5 REVIEW

|| ||

341

Stewart J. Calculus

Подождите немного. Документ загружается.