Stewart J. Calculus
Подождите немного. Документ загружается.


23. 24.
25. 26.
27. 28.
;
29–30 Evaluate the indefinite integral. Illustrate and check that
your answer is reasonable by graphing both the function and its
antiderivative (take ).
29. 30.
;
31. Use a graph to give a rough estimate of the area of the region
that lies under the curve . Then find the
exact area.
;
32. Graph the function and use the graph to
guess the value of the integral . Then evaluate the
integral to confirm your guess.
33 –38 Find the derivative of the function.
33. 34.
35. 36.
37. 38.
39 – 40 Use Property 8 of integrals to estimate the value of the
integral.
39. 40.
41– 42 Use the properties of integrals to verify the inequality.
41. 42.
43. Use the Midpoint Rule with to approximate
.
44. A particle moves along a line with velocity function
, where is measured in meters per second.
Find (a) the displacement and (b) the distance traveled by
the particle during the time interval .$0, 5%
vv!t" ! t
2
! t
x
3
0
sin!x
3
" dx
n ! 6
y
#
#2
#
#4
sin x
x
dx $
s
2
2
y
1
0
x
2
cos x dx $
1
3
y
5
3
1
x " 1
dx
y
3
1
s
x
2
" 3
dx
y !
y
3x"1
2x
sin!t
4
" dty !
y
x
s
x
cos
'
'
d
'
t!x" !
y
sin x
1
1 ! t
2
1 " t
4
dtt!x" !
y
x
4
0
cos!t
2
" dt
F!x" !
y
1
x
s
t " sin t
dtF!x" !
y
x
0
t
2
1 " t
3
dt
x
2
#
0
f !x" dx
f !x" ! cos
2
x sin
3
x
y ! x
s
x
, 0 $ x $ 4
y
x
3
s
x
2
" 1
dx
y
cos x
s
1 " sin x
dx
C ! 0
y
4
0
&
s
x
! 1
&
dx
y
3
0
&
x
2
! 4
&
dx
y
#
#4
0
!1 " tan t"
3
sec
2
t dt
y
#
#8
0
sec 2
'
tan 2
'
d
'
y
sin x cos!cos x" dx
y
sin
#
t cos
#
t dt
5. If and , find .
6. (a) Write as a limit of Riemann sums,
taking the sample points to be right endpoints. Use a
computer algebra system to evaluate the sum and to
compute the limit.
(b) Use the Fundamental Theorem to check your answer to
part (a).
7. The following figure shows the graphs of , and
. Identify each graph, and explain your choices.
8. Evaluate:
(a)
(b)
(c)
9–28 Evaluate the integral, if it exists.
9. 10.
11. 12.
13. 14.
15. 16.
17. 18.
19. 20.
21. 22.
y
x " 2
s
x
2
" 4x
dx
y
#
#4
!
#
#4
t
4
tan t
2 " cos t
dt
y
1
!1
sin x
1 " x
2
dx
y
1
0
v
2
cos!v
3
" dv
y
1
0
sin!3
#
t" dt
y
5
1
dt
!t ! 4"
2
y
2
0
y
2
s
1 " y
3
dy
y
1
0
y!y
2
" 1"
5
dy
y
1
0
(
s
4
u
" 1"
2
du
y
9
1
s
u
! 2u
2
u
du
y
1
0
!1 ! x"
9
dx
y
1
0
!1 ! x
9
" dx
y
T
0
!x
4
! 8x " 7" dx
y
2
1
!8x
3
" 3x
2
" dx
d
dx
y
#
#2
x
sin
t
2
cos
t
3
dt
d
dx
y
#
#2
0
sin
x
2
cos
x
3
dx
y
#
#2
0
d
dx
(
sin
x
2
cos
x
3
)
dx
y
x
a
b
c
x
x
0
f !t" dt
f, f *
x
5
1
!x " 2x
5
" dx
CAS
x
6
4
f !x" dxx
4
0
f !x" dx ! 7x
6
0
f !x" dx ! 10
342
|| ||
CHAPTER 5 INTEGRALS
50.
The Fresnel function was introduced
in Section 5.3. Fresnel also used the function
in his theory of the diffraction of light waves.
(a) On what intervals is increasing?
(b) On what intervals is concave upward?
(c) Use a graph to solve the following equation correct to two
decimal places:
(d) Plot the graphs of and on the same screen. How are
these graphs related?
51.
If is a continuous function such that
for all , find an explicit formula for .
52.
Find a function and a value of the constant such that
53.
If is continuous on , show that
54.
Find .
55.
If is continuous on , prove that
56.
Evaluate
lim
n l +
1
n
+(
1
n
)
9
"
(
2
n
)
9
"
(
3
n
)
9
" - - - "
(
n
n
)
9
,
y
1
0
f !x" dx !
y
1
0
f !1 ! x" dx
$0, 1%f
lim
h
l
0
1
h
y
2"h
2
s
1 " t
3
dt
2
y
b
a
f !x" f *!x" dx ! $ f !b"%
2
! $ f !a"%
2
$a, b%f *
2
y
x
a
f !t" dt ! 2 sin x ! 1
af
f !x"x
y
x
0
f !t" dt ! x sin x "
y
x
0
f !t"
1 " t
2
dt
f
SC
CAS
y
x
0
cos
(
1
2
#
t
2
)
dt ! 0.7
CAS
C
C
C!x" !
y
x
0
cos
(
1
2
#
t
2
)
dt
S!x" !
x
x
0
sin
(
1
2
#
t
2
)
dt
45.
Let be the rate at which the world’s oil is consumed,
where is measured in years starting at on January 1,
2000, and is measured in barrels per year. What does
represent?
46.
A radar gun was used to record the speed of a runner at the
times given in the table. Use the Midpoint Rule to estimate
the distance the runner covered during those 5 seconds.
47.
A population of honeybees increased at a rate of bees per
week, where the graph of r is as shown. Use the Midpoint
Rule with six subintervals to estimate the increase in the bee
population during the first 24 weeks.
48.
Let
Evaluate by interpreting the integral as a
difference of areas.
49.
If is continuous and , evaluate
.
x
#
#2
0
f !2 sin
'
"
cos
'
d
'
x
2
0
f !x" dx ! 6f
x
1
!3
f !x" dx
f !x" !
-
!x ! 1
!
s
1 ! x
2
if !3 $ x $ 0
if 0 $ x $ 1
r
0
2420161284
(weeks)
t
4000
8000
12000
r!t"
x
8
0
r!t" dt
r!t"
t ! 0t
r!t"
CHAPTER 5 REVIEW
|| ||
343
t (s) (m#s) t (s) (m#s)
0 0 3.0 10.51
0.5
4.67 3.5 10.67
1.0
7.34 4.0 10.76
1.5
8.86 4.5 10.81
2.0
9.73 5.0 10.81
2.5 10.22
vv
Openmirrors.com
344
Before you look at the solution of the following example, cover it up and first try to solve
the problem yourself.
EXAMPLE 1 Evaluate .
SOLUTION Let’s start by having a preliminary look at the ingredients of the function. What
happens to the first factor, , when approaches ? The numerator approaches
and the denominator approaches , so we have
and
The second factor approaches , which is . It’s not clear what happens to the
function as a whole. (One factor is becoming large while the other is becoming small.)
So how do we proceed?
One of the principles of problem solving is recognizing something familiar. Is there a
part of the function that reminds us of something we’ve seen before? Well, the integral
has as its upper limit of integration and that type of integral occurs in Part 1 of the
Fundamental Theorem of Calculus:
This suggests that differentiation might be involved.
Once we start thinking about differentiation, the denominator reminds us of
something else that should be familiar: One of the forms of the definition of the deriva-
tive in Chapter 3 is
and with this becomes
So what is the function in our situation? Notice that if we define
then . What about the factor in the numerator? That’s just a red herring, so
let’s factor it out and put together the calculation:
(FTC1)
M
! sin 3
! 3
sin 3
3
! 3F*!3"
! 3 lim
x l 3
F!x" ! F!3"
x ! 3
lim
x l 3
(
x
x ! 3
y
x
3
sin t
t
dt
)
! lim
x l 3
x ! lim
x l 3
y
x
3
sin t
t
dt
x ! 3
xF!3" ! 0
F!x" !
y
x
3
sin t
t
dt
F
F*!3" ! lim
x l 3
F!x" ! F!3"
x ! 3
a ! 3
F*!a" ! lim
x l a
F!x" ! F!a"
x ! a
!x ! 3"
d
dx
y
x
a
f !t" dt ! f !x"
x
y
x
3
sin t
t
dt
0
x
3
3
!sin t"#t dt
x l 3
!
as
x
x ! 3
l !+x l 3
"
as
x
x ! 3
l +
0
33xx#!x ! 3"
lim
x l 3
(
x
x ! 3
y
x
3
sin t
t
dt
)
P R O B L E M S P L U S
N The principles of problem solving are
discussed on page 54.

345
1. If , where is a continuous function, find .
2. Find the maximum value of the area of the region under the curve from to
, for all .
3. If is a differentiable function such that is never and for all , find .
;
4. (a) Graph several members of the family of functions for and look
at the regions enclosed by these curves and the -axis. Make a conjecture about how the areas
of these regions are related.
(b) Prove your conjecture in part (a).
(c) Take another look at the graphs in part (a) and use them to sketch the curve traced out by the
vertices (highest points) of the family of functions. Can you guess what kind of curve this is?
(d) Find an equation of the curve you sketched in part (c).
5. If , where , find .
6. If , find .
7. Find the interval for which the value of the integral is a maximum.
8. Use an integral to estimate the sum .
9. (a) Evaluate , where is a positive integer.
(b) Evaluate , where and are real numbers with .
10. Find .
11. Suppose the coefficients of the cubic polynomial satisfy the equation
Show that the equation has a root between 0 and 1. Can you generalize this result for an
-degree polynomial?
12. A circular disk of radius is used in an evaporator and is rotated in a vertical plane. If it is to be
partially submerged in the liquid so as to maximize the exposed wetted area of the disk, show that
the center of the disk should be positioned at a height above the surface of the liquid.
13. Prove that if is continuous, then .
14. The figure shows a region consisting of all points inside a square that are closer to the center than
to the sides of the square. Find the area of the region.
15. Evaluate .
16. For any number , we let be the smaller of the two numbers and . Then
we define . Find the maximum and minimum values of if .!2 $ c $ 2t!c"t!c" !
x
1
0
f
c
!x" dx
!x ! c ! 2"
2
!x ! c"
2
f
c
!x"c
lim
n l +
(
1
s
n
s
n " 1
"
1
s
n
s
n " 2
" - - - "
1
s
n
s
n " n
)
y
x
0
f !u"!x ! u" du !
y
x
0
(y
u
0
f !t" dt
)
duf
r#
s
1 "
#
2
r
nth
P!x" ! 0
a "
b
2
"
c
3
"
d
4
! 0
P!x" ! a " bx " cx
2
" dx
3
d
2
dx
2
y
x
0
(y
sin t
1
s
1 " u
4
du
)
dt
0 $ a
)
bba
x
b
a
.x/ dx
n
x
n
0
.x/ dx
*
10000
i!1
s
i
x
b
a
!2 " x ! x
2
" dx$a, b%
f *!x"f !x" ! x
x
0
x
2
sin!t
2
" dt
f *!
#
#2"t!x" !
y
cos x
0
$1 " sin!t
2
"% dtf !x" !
y
t!x"
0
1
s
1 " t
3
dt
x
c & 0f !x" ! !2cx ! x
2
"#c
3
fx
y
x
0
f !t" dt ! $ f !x"%
2
0f !x"f
a & 0x ! a " 1
x ! ay ! 4x ! x
3
f !4"fx sin
#
x !
y
x
2
0
f !t" dt
PROBLEM S
P R O B L E M S P L U S
F I G U R E F O R P RO B LE M 1 4
22
2
2
346
In this chapter we explore some of the applications of the definite integral, such as
computing areas between curves, volumes of solids, and the work done by a varying
force. The common theme is the following general method, which is similar to the one
we used to find areas under curves: We break up a quantity into a large number of
small parts. We next approximate each small part by a quantity of the form and
thus approximate by a Riemann sum. Then we take the limit and express as an
integral. Finally we evaluate the integral using the Fundamental Theorem of Calculus
or the Midpoint Rule.
QQ
f 共x
i
*
兲 ⌬x
Q
The volume of a sphere is
the limit of sums of volumes
of approximating cylinders.
APPLICATIONS OF
INTEGRATION
6
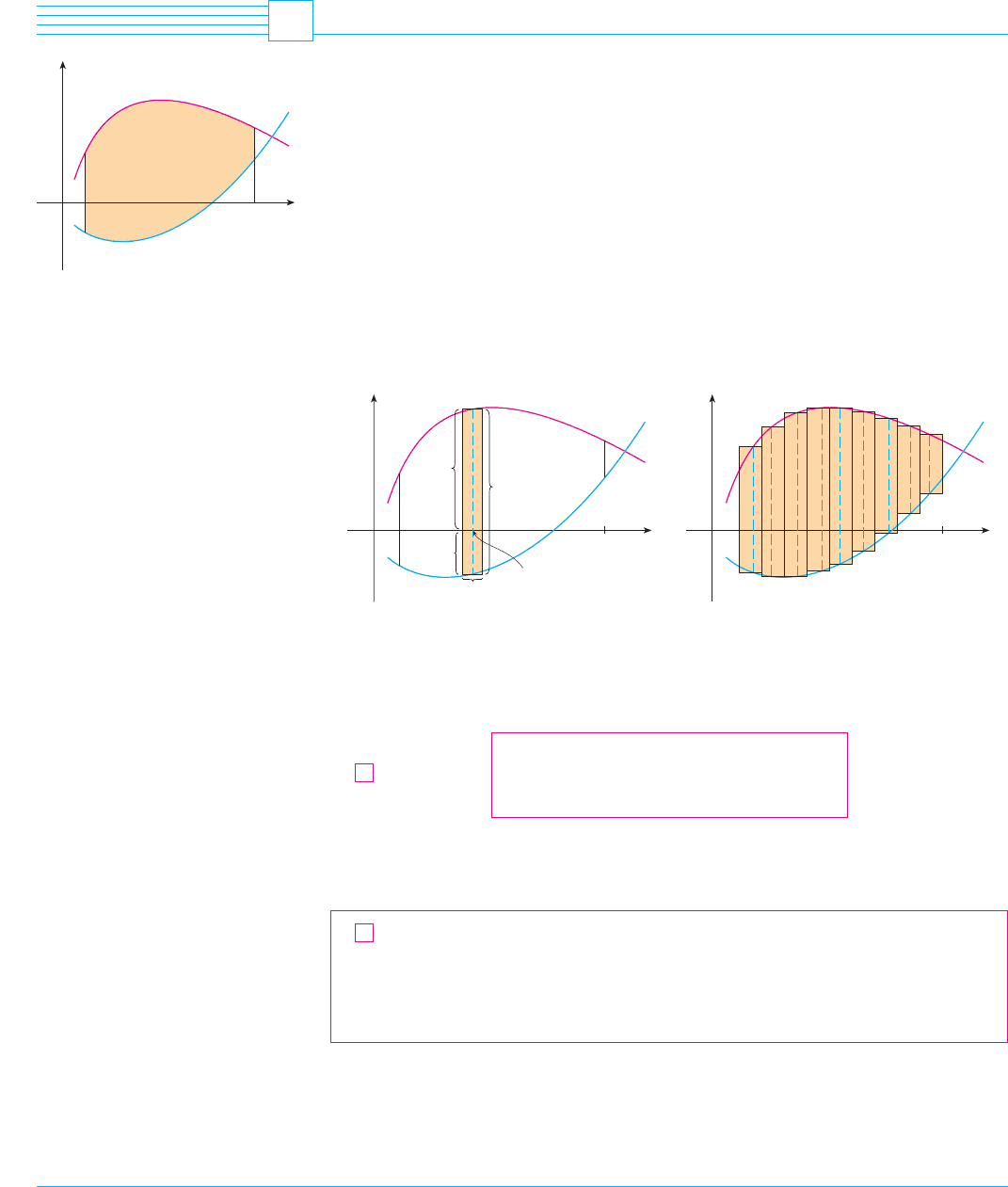
0
y=©
y=ƒ
S
FIGURE 1
S=s(x,y)|a¯x¯b, ©¯y¯ƒd
x
y
ba
AREAS BETWEEN CURVES
In Chapter 5 we defined and calculated areas of regions that lie under the graphs of
functions. Here we use integrals to find areas of regions that lie between the graphs of two
functions.
Consider the region that lies between two curves and and be-
tween the vertical lines and , where and are continuous functions and
for all in . (See Figure 1.)
Just as we did for areas under curves in Section 5.1, we divide S into n strips of equal
width and then we approximate the ith strip by a rectangle with base and height
. (See Figure 2. If we like, we could take all of the sample points to be right
endpoints, in which case .) The Riemann sum
is therefore an approximation to what we intuitively think of as the area of S.
This approximation appears to become better and better as . Therefore we define
the area of the region as the limiting value of the sum of the areas of these approxi-
mating rectangles.
We recognize the limit in (1) as the definite integral of . Therefore we have the fol-
lowing formula for area.
The area A of the region bounded by the curves , and the
lines , , where and are continuous and for all in , is
Notice that in the special case where , is the region under the graph of
and our general definition of area (1) reduces to our previous definition (Definition 2 in
Section 5.1).
fSt共x兲 苷 0
A 苷
y
b
a
关 f 共x兲 ⫺ t共x兲兴 dx
关a, b兴xf 共x兲 艌 t共x兲tfx 苷 bx 苷 a
y 苷 f 共x兲, y 苷 t共x兲
2
f ⫺ t
A 苷 lim
n l ⬁
兺
n
i苷1
关 f 共x
i
*
兲 ⫺ t共x
i
*
兲兴 ⌬x
1
SA
n l ⬁
(a) Typical rectangle
x
y
b
0
a
f(x
i
*
)
f(x
i
*
)-g(x
i
*
)
_g(x
i
*
)
x
i
*
Îx
(b) Approximating rectangles
x
y
b
0
a
FIGURE 2
兺
n
i苷1
关 f 共x
i
*
兲 ⫺ t共x
i
*
兲兴 ⌬x
x
i
*
苷 x
i
f 共x
i
*
兲 ⫺ t共x
i
*
兲
⌬x
关a, b兴xf 共x兲 艌 t共x兲
tfx 苷 bx 苷 a
y 苷 t共x兲y 苷 f 共x兲S
6.1
347
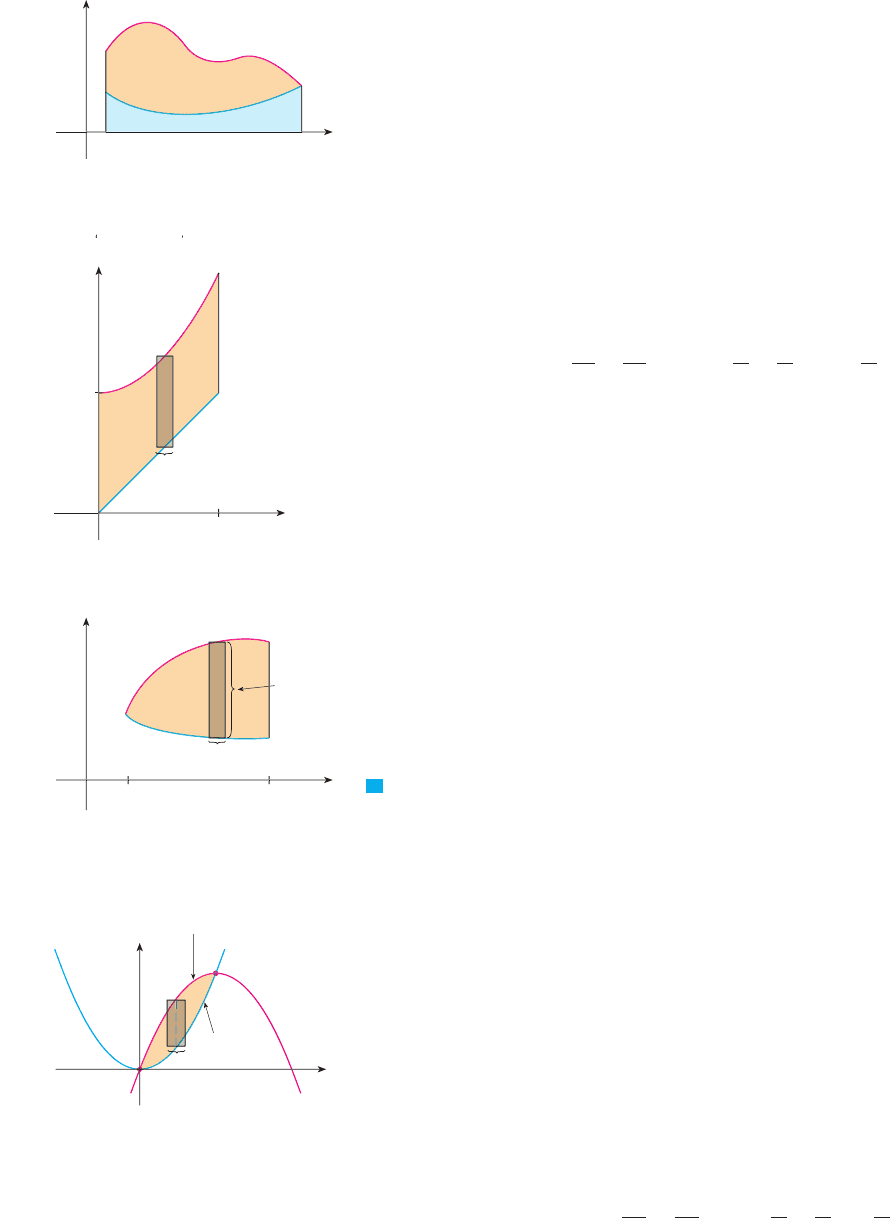
In the case where both and are positive, you can see from Figure 3 why (2) is true:
EXAMPLE 1 Find the area of the region bounded above by , bounded below
by , and bounded on the sides by x 苷 0 and x 苷 1.
SOLUTION The region is shown in Figure 4. The upper boundary curve is and
the lower boundary curve is y 苷 x. So we use the area formula (2) with ,
, and :
M
In Figure 4 we drew a typical approximating rectangle with width as a reminder of
the procedure by which the area is defined in (1). In general, when we set up an integral
for an area, it’s helpful to sketch the region to identify the top curve , the bottom curve
, and a typical approximating rectangle as in Figure 5. Then the area of a typical rect-
angle is and the equation
summarizes the procedure of adding (in a limiting sense) the areas of all the typical
rectangles.
Notice that in Figure 5 the left-hand boundary reduces to a point, whereas in Figure 3
the right-hand boundary reduces to a point. In the next example both of the side bound-
aries reduce to a point, so the first step is to find a and b.
EXAMPLE 2 Find the area of the region enclosed by the parabolas and
.
SOLUTION We first find the points of intersection of the parabolas by solving their equa-
tions simultaneously. This gives , or . Thus ,
so or 1. The points of intersection are and .
We see from Figure 6 that the top and bottom boundaries are
and
The area of a typical rectangle is
and the region lies between and . So the total area is
M
苷 2
冋
x
2
2
⫺
x
3
3
册
0
1
苷 2
冉
1
2
⫺
1
3
冊
苷
1
3
A 苷
y
1
0
共2x ⫺ 2x
2
兲 dx 苷 2
y
1
0
共x ⫺ x
2
兲 dx
x 苷 1x 苷 0
共y
T
⫺ y
B
兲 ⌬x 苷 共2x ⫺ x
2
⫺ x
2
兲 ⌬x
y
B
苷 x
2
y
T
苷 2x ⫺ x
2
共1, 1兲共0, 0兲x 苷 0
2x共x ⫺ 1兲 苷 02x
2
⫺ 2x 苷 0x
2
苷 2x ⫺ x
2
y 苷 2x ⫺ x
2
y 苷 x
2
V
A 苷 lim
n
l
⬁
兺
n
i苷1
共y
T
⫺ y
B
兲 ⌬x 苷
y
b
a
共y
T
⫺ y
B
兲 dx
共y
T
⫺ y
B
兲 ⌬x
y
B
y
T
⌬x
苷
x
3
3
⫺
x
2
2
⫹ x
册
0
1
苷
1
3
⫺
1
2
⫹ 1 苷
5
6
A 苷
y
1
0
关共x
2
⫹ 1兲 ⫺ x兴 dx 苷
y
1
0
共x
2
⫺ x ⫹ 1兲 dx
b 苷 1a 苷 0, t共x兲 苷 x
f 共x兲 苷 x
2
⫹ 1
y 苷 x
2
⫹ 1
y 苷 x
y 苷 x
2
⫹ 1
苷
y
b
a
f 共x兲 dx ⫺
y
b
a
t共x兲 dx 苷
y
b
a
关 f 共x兲 ⫺ t共x兲兴 dx
A 苷 关area under y 苷 f 共x兲兴 ⫺ 关area under y 苷 t共x兲兴
tf
348
||||
CHAPTER 6 APPLICATIONS OF INTEGRATION
FI
GU
RE
3
A=
j
ƒ
d
x
-
j
©
d
x
a
j
j
b
a
j
j
b
0
x
y
a
b
y=ƒ
y=©
S
Î
x
(0
, 0
)
(1
,
1
)
FI
GU
RE
6
y
T
=
2x
-
≈
y
B
=
≈
x
y
0
x
y
a
b
y
T
y
B
y
T
-y
B
Îx
FI
G
URE
5
F
I
G
URE
4
x=1
1
0
x
y
1
y=≈+1
y=x
Îx
x=0

Sometimes it’s difficult, or even impossible, to find the points of intersection of two
curves exactly. As shown in the following example, we can use a graphing calculator or
computer to find approximate values for the intersection points and then proceed as before.
EXAMPLE 3 Find the approximate area of the region bounded by the curves
and
SOLUTION If we were to try to find the exact intersection points, we would have to solve
the equation
This looks like a very difficult equation to solve exactly (in fact, it’s impossible), so
instead we use a graphing device to draw the graphs of the two curves in Figure 7. One
intersection point is the origin. We zoom in toward the other point of intersection and
find that . (If greater accuracy is required, we could use Newton’s method or a
rootfinder, if available on our graphing device.) Thus an approximation to the area
between the curves is
To integrate the first term we use the subsitution . Then , and
when . So
M
EXAMPLE 4 Figure 8 shows velocity curves for two cars, A and B, that start side by side
and move along the same road. What does the area between the curves represent? Use
the Midpoint Rule to estimate it.
SOLUTION We know from Section 5.4 that the area under the velocity curve A represents
the distance traveled by car A during the first 16 seconds. Similarly, the area under curve
B is the distance traveled by car B during that time period. So the area between these
curves, which is the difference of the areas under the curves, is the distance between the
cars after 16 seconds. We read the velocities from the graph and convert them to feet per
second .共1 mi兾h 苷
5280
3600
ft兾s兲
⬇ 0.785
苷
s
2.39 ⫺ 1 ⫺
共1.18兲
5
5
⫹
共1.18兲
2
2
苷
s
u
]
1
2.39
⫺
冋
x
5
5
⫺
x
2
2
册
0
1.18
A ⬇
1
2
y
2.39
1
du
s
u
⫺
y
1.18
0
共x
4
⫺ x兲 dx
x 苷 1.18, we have u ⬇ 2.39
du 苷 2xdxu 苷 x
2
⫹ 1
A ⬇
y
1.18
0
冋
x
s
x
2
⫹ 1
⫺ 共x
4
⫺ x兲
册
dx
x ⬇ 1.18
x
s
x
2
⫹ 1
苷 x
4
⫺ x
y 苷 x
4
⫺ x.y 苷 x兾
s
x
2
⫹ 1
SECTION 6.1 AREAS BETWEEN CURVES
||||
349
1.5
_1
_1 2
y=x$-x
x
œ„„„„„
≈+1
FIGURE 7
y=
t 0 2 4 6 8 10 12 14 16
03454677684899295
02134445156606365
01320232528292930
v
A
⫺ v
B
v
B
v
A
FIGURE 8
0
10
20
30
40
50
60
A
B
2 4 6 8 10 12 14 16
t
(seconds)
√ (mi/h)

We use the Midpoint Rule with intervals, so that . The midpoints of the
intervals are , , , and . We estimate the distance between the
cars after 16 seconds as follows:
M
If we are asked to find the area between the curves and where
for some values of but for other values of , then we split the
given region into several regions , ,...with areas , ,...as shown in Figure 9.
We then define the area of the region to be the sum of the areas of the smaller regions
, ,...,that is, . Since
we have the following expression for A.
The area between the curves and and between and
is
When evaluating the integral in (3), however, we must still split it into integrals corre-
sponding to , ,....
EXAMPLE 5 Find the area of the region bounded by the curves , ,
, and .
SOLUTION The points of intersection occur when , that is, when
(since ). The region is sketched in Figure 10. Observe that
when but when . Therefore the required
area is
In this particular example we could have saved some work by noticing that the region
is symmetric about and so
MA 苷 2A
1
苷 2
y
兾4
0
共cos x ⫺ sin x兲 dx
x 苷
兾4
苷 2
s
2 ⫺ 2
苷
冉
1
s
2
⫹
1
s
2
⫺ 0 ⫺ 1
冊
⫹
冉
⫺0 ⫺ 1 ⫹
1
s
2
⫹
1
s
2
冊
苷
[
sin x ⫹ cos x
]
0
兾4
⫹
[
⫺cos x ⫺ sin x
]
兾4
兾2
苷
y
兾4
0
共cos x ⫺ sin x兲 dx ⫹
y
兾2
兾4
共sin x ⫺ cos x兲 dx
A 苷
y
兾2
0
ⱍ
cos x ⫺ sin x
ⱍ
dx 苷 A
1
⫹ A
2
兾4 艋 x 艋
兾2sin x 艌 cos x0 艋 x 艋
兾4
cos x 艌 sin x0 艋 x 艋
兾2
x 苷
兾4sin x 苷 cos x
x 苷
兾2x 苷 0
y 苷 cos xy 苷 sin x
V
A
2
A
1
A 苷
y
b
a
ⱍ
f 共x兲 ⫺ t共x兲
ⱍ
dx
x 苷 b
x 苷 ay 苷 t共x兲y 苷 f 共x兲
3
ⱍ
f 共x兲 ⫺ t共x兲
ⱍ
苷
再
f 共x兲 ⫺ t共x兲
t共x兲 ⫺ f 共x兲
when f 共x兲 艌 t共x兲
when t共x兲 艌 f 共x兲
A 苷 A
1
⫹ A
2
⫹⭈⭈⭈S
2
S
1
S
A
2
A
1
S
2
S
1
S
xt共x兲 艌 f 共x兲xf 共x兲 艌 t共x兲
y 苷 t共x兲y 苷 f 共x兲
苷 4共93兲 苷 372 ft
y
16
0
共v
A
⫺ v
B
兲 dt ⬇ ⌬t 关13 ⫹ 23 ⫹ 28 ⫹ 29兴
t
4
苷 14t
3
苷 10t
2
苷 6t
1
苷 2
⌬t 苷 4n 苷 4
350
||||
CHAPTER 6 APPLICATIONS OF INTEGRATION
0
x
y
a
b
y=ƒ
y=©
S¡
S™
S£
FIGURE 9
FIGURE 10
0
x
y
x=0
A¡
y =cosx
y=sin x
A™
π
4
π
2
x=
π
2
Some regions are best treated by regarding x as a function of y. If a region is bounded
by curves with equations , , , and , where and are contin-
uous and for (see Figure 11), then its area is
If we write for the right boundary and for the left boundary, then, as Figure 12
illustrates, we have
Here a typical approximating rectangle has dimensions and .
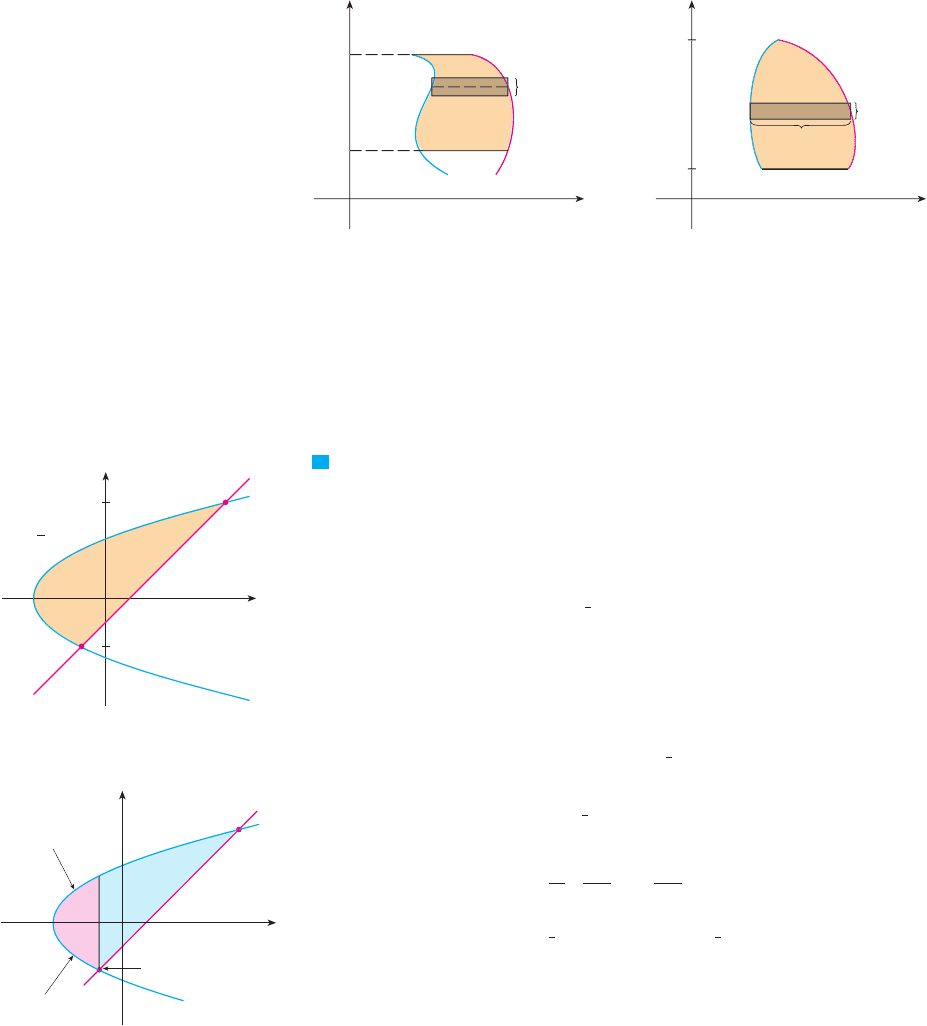
EXAMPLE 6 Find the area enclosed by the line and the parabola
.
SOLUTION By solving the two equations we find that the points of intersection are
and . We solve the equation of the parabola for x and notice from
Figure 13 that the left and right boundary curves are
We must integrate between the appropriate -values, and . Thus
M
We could have found the area in Example 6 by integrating with respect to x instead of
y, but the calculation is much more involved. It would have meant splitting the region in
two and computing the areas labeled and in Figure 14. The method we used in
Example 6 is much easier.
A
2
A
1
苷 ⫺
1
6
共64兲 ⫹ 8 ⫹ 16 ⫺
(
4
3
⫹ 2 ⫺ 8
)
苷 18
苷 ⫺
1
2
冉
y
3
3
冊
⫹
y
2
2
⫹ 4y
册
⫺2
4
苷
y
4
⫺2
(
⫺
1
2
y
2
⫹ y ⫹ 4
)
dy
苷
y
4
⫺2
[
共y ⫹ 1兲 ⫺
(
1
2
y
2
⫺ 3
)
]
dy
A 苷
y
4
⫺2
共x
R
⫺ x
L
兲 dy
y 苷 4y 苷 ⫺2y
x
R
苷 y ⫹ 1x
L
苷
1
2
y
2
⫺ 3
共5, 4兲共⫺1, ⫺2兲
y
2
苷 2x ⫹ 6
y 苷 x ⫺ 1
V
⌬yx
R
⫺ x
L
A 苷
y
d
c
共x
R
⫺ x
L
兲 dy
x
L
x
R
x
c
d
y
0
y=
d
x
=
g(
y
)
x=
f
(
y)
y
=
c
Î
y
FI
GU
RE 1
1
0
x
y
c
d
x
R
x
L
x
R
-x
L
Îy
FI
GU
RE 1
2
A 苷
y
d
c
关 f 共y兲 ⫺ t共y兲兴 dy
c 艋 y 艋 df 共y兲 艌 t共y兲
tfy 苷 dy 苷 cx 苷 t共y兲x 苷 f 共y兲
SECTION 6.1 AREAS BETWEEN CURVES
||||
351
x
y
_2
4
0
(_1, _2)
(5, 4)
x
R
=y+1
1
2
x
L
=
¥-3
FIGURE 13
⫺3
(5,4)
(_1, _2)
y=x-1
A¡
y=_ 2x+6
A™
y= 2x+6
œ
„„„„„
œ
„„„„„
FIGURE 14
0
x
y
