Stewart J. Calculus
Подождите немного. Документ загружается.

we would have obtained the integral
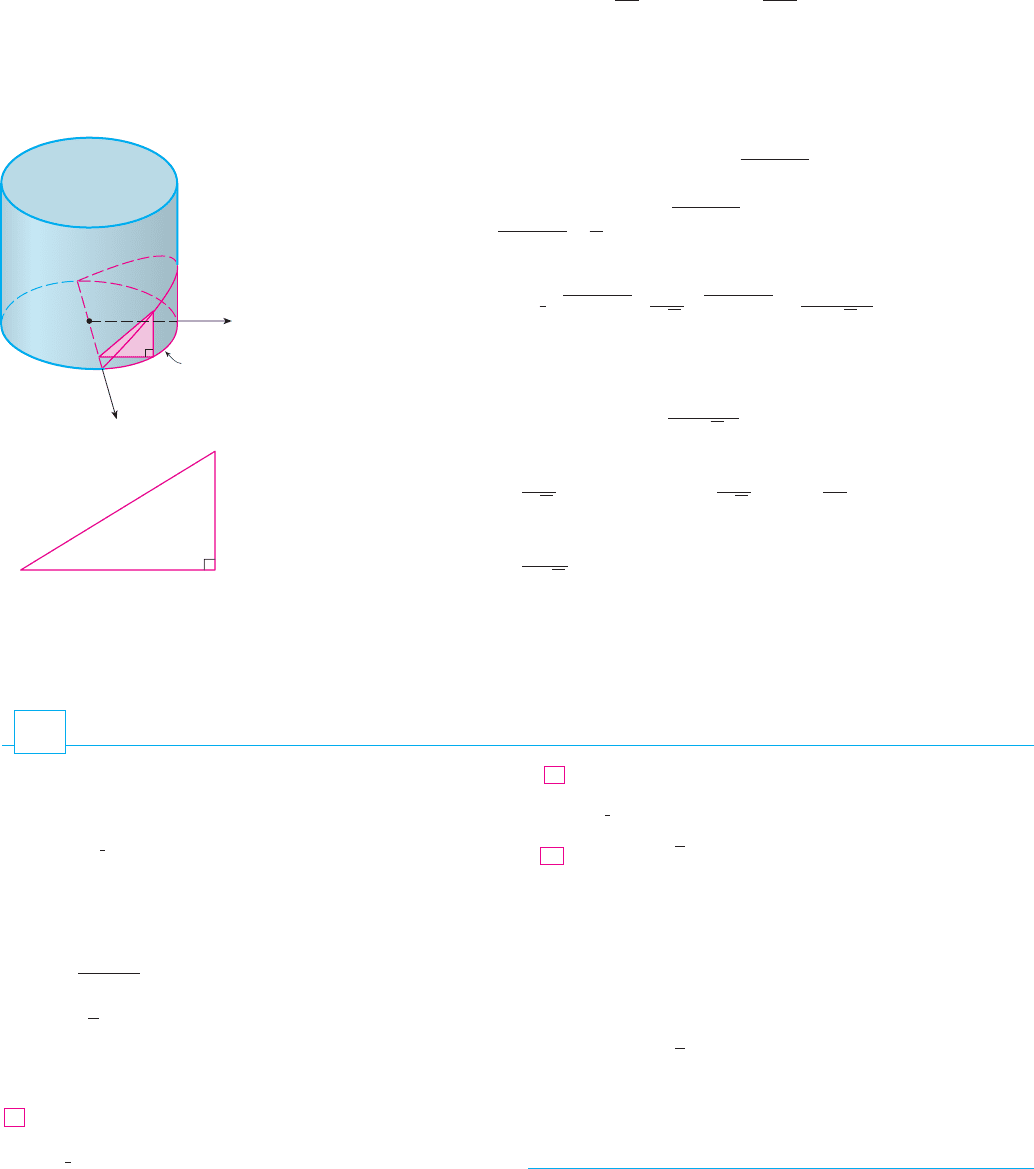
EXAMPLE 9 A wedge is cut out of a circular cylinder of radius 4 by two planes. One
plane is perpendicular to the axis of the cylinder. The other intersects the first at an angle
of 30 along a diameter of the cylinder. Find the volume of the wedge.
SOLUTION If we place the -axis along the diameter where the planes meet, then the
base of the solid is a semicircle with equation , . A cross-
section perpendicular to the -axis at a distance from the origin is a triangle ,
as shown in Figure 17, whose base is and whose height is
. Thus the cross-sectional area is
and the volume is
For another method see Exercise 64. M
苷
128
3
s
3
苷
1
s
3
y
4
0
共16 ⫺ x
2
兲 dx 苷
1
s
3
冋
16x ⫺
x
3
3
册
0
4
V 苷
y
4
⫺4
A共x兲 dx 苷
y
4
⫺4
16 ⫺ x
2
2
s
3
dx
苷
16 ⫺ x
2
2
s
3
A共x兲 苷
1
2
s
16 ⫺ x
2
ⴢ
1
s
3
s
16 ⫺ x
2
ⱍ
BC
ⱍ
苷 y tan 30⬚ 苷
s
16 ⫺ x
2
兾
s
3
y 苷
s
16 ⫺ x
2
ABCxx
⫺4 艋 x 艋 4y 苷
s
16 ⫺ x
2
x
⬚
V 苷
y
h
0
L
2
h
2
共h ⫺ y兲
2
dy 苷
L
2
h
3
362
||||
CHAPTER 6 APPLICATIONS OF INTEGRATION
y=œ„„„„„„16-≈
x
y
0
A
B
C
4
FIGURE 17
A B
C
y
30°
, ; about the -axis
10. , , ; about the -axis
, ; about
12. , ; about
13. , ; about
14. , , , ; about
15. , ; about
16. , ; about
17. , ; about
18. , , , ; about x 苷 1x 苷 4x 苷 2y 苷 0y 苷 x
x 苷 ⫺1x 苷 y
2
y 苷 x
2
x 苷 2y 苷
s
x
y 苷 x
x 苷 1x 苷 1x 苷 y
2
y 苷 ⫺1x 苷 3x 苷 1y 苷 0y 苷 1兾x
y 苷 1y 苷 3y 苷 1 ⫹ sec x
y 苷 4y 苷 4y 苷 x
2
y 苷 1y 苷
s
x
y 苷 x
11.
yy 苷 0x 苷 2y 苷
1
4
x
2
yx 苷 2yy
2
苷 x
9.
1–18 Find the volume of the solid obtained by rotating the region
bounded by the given curves about the specified line. Sketch the
region, the solid, and a typical disk or washer.
1. ,,,;about the -axis
2. , ; about the -axis
3. , , , ; about the -axis
4. , , , ; about the -axis
5. , , ; about the -axis
6. , ; about the -axis
, , ; about the -axis
8. , ; about the -axisxy 苷 5 ⫺ x
2
y 苷
1
4
x
2
xx 艌 0y 苷 xy 苷 x
3
7.
yx 苷 0x 苷 y ⫺ y
2
yy 苷 9x 苷 0x 苷 2
s
y
xx 苷 4x 苷 2y 苷 0y 苷
s
25 ⫺ x
2
xy 苷 0x 苷 2x 苷 1y 苷 1兾x
xy 苷 0y 苷 1 ⫺ x
2
xx 苷 2x 苷 1y 苷 0y 苷 2 ⫺
1
2
x
EXERCISES
6.2

44.
45. A CAT scan produces equally spaced cross-sectional views of
a human organ that provide information about the organ other-
wise obtained only by surgery. Suppose that a CAT scan of a
human liver shows cross-sections spaced 1.5 cm apart. The
liver is 15 cm long and the cross-sectional areas, in square
centimeters, are 0, 18, 58, 79, 94, 106, 117, 128, 63, 39, and
0. Use the Midpoint Rule to estimate the volume of the liver.
46. A log 10 m long is cut at 1-meter intervals and its cross-
sectional areas (at a distance from the end of the log) are
listed in the table. Use the Midpoint Rule with to esti-
mate the volume of the log.
47. (a) If the region shown in the figure is rotated about the
-axis to form a solid, use the Midpoint Rule with
to estimate the volume of the solid.
(b) Estimate the volume if the region is rotated about the
-axis. Again use the Midpoint Rule with .
48. (a) A model for the shape of a bird’s egg is obtained by
rotating about the -axis the region under the graph of
Use a CAS to find the volume of such an egg.
(b) For a Red-throated Loon, , , ,
and . Graph and find the volume of an egg of
this species.
49–61 Find the volume of the described solid .
A right circular cone with height and base radius
50. A frustum of a right circular cone with height , lower base
radius , and top radius
R
h
r
rR
h
rh
49.
S
fd 苷 0.54
c 苷 0.1b 苷 0.04a 苷 ⫺0.06
f 共x兲 苷 共ax
3
⫹ bx
2
⫹ cx ⫹ d兲
s
1 ⫺ x
2
x
CAS
n 苷 4y
0
4
4
10
2
86
2
y
x
n 苷 4x
n 苷 5
xA
y
兾2
0
关共1 ⫹ cos x兲
2
⫺ 1
2
兴 dx
y
1
0
共y
4
⫺ y
8
兲 dy
43.
19–30 Refer to the figure and find the volume generated by
rotating the given region about the specified line.
19. about 20. about
21. about 22. about
23. about 24. about
25. about 26. about
27. about 28. about
29. about 30. about
31–36 Set up, but do not evaluate, an integral for the volume of
the solid obtained by rotating the region bounded by the given
curves about the specified line.
31.
32.
, ; about
33. , , ; about
34. , , ; about
35. , ; about
36. , , ; about
;
37–38 Use a graph to find approximate -coordinates of the
points of intersection of the given curves. Then use your calcula-
tor to find (approximately) the volume of the solid obtained by
rotating about the -axis the region bounded by these curves.
37. ,
38. ,
39– 40 Use a computer algebra system to find the exact volume
of the solid obtained by rotating the region bounded by the given
curves about the specified line.
39. ,, ;
40. ,;
41– 44 Each integral represents the volume of a solid. Describe
the solid.
41. 42.
y
5
2
ydy
y
兾2
0
cos
2
xdx
about y 苷 2y 苷 x cos共
x兾4兲y 苷 x
2
⫺ 2x
about y 苷 ⫺10 艋 x 艋
y 苷 0y 苷 sin
2
x
CAS
y 苷 3x ⫺ x
3
y 苷 x
4
y 苷 x
4
⫹ x ⫹ 1y 苷 2 ⫹ x
2
cos x
x
x
y 苷 40 艋 x 艋 2
y 苷 2 ⫺ cos xy 苷 cos x
x 苷 ⫺2x 苷 3x
2
⫺ y
2
苷 1
y 苷 ⫺20 艋 x 艋
y 苷 sin xy 苷 0
y 苷 10 艋 x 艋
y 苷 sin xy 苷 0
x 苷 108x ⫺ y 苷 16y 苷 共x ⫺ 2兲
4
y 苷 tan
3
x, y 苷 1, x 苷 0; about y 苷 1
BC
3
AB
3
OC
3
OA
3
BC
2
AB
2
OC
2
OA
2
BC
1
AB
1
OC
1
OA
1
O
x
y
T™
y=˛
T£
T¡
B(1,1)
A(1,0)
y=
œ„
x
C(0,1)
SECTION 6.2 VOLUMES
||||
363
x (m) A () x (m) A ()
0 0.68 6 0.53
1
0.65 7 0.55
2
0.64 8 0.52
3
0.61 9 0.50
4
0.58 10 0.48
50.59
m
2
m
2
364
||||
CHAPTER 6 APPLICATIONS OF INTEGRATION
62. The base of is a circular disk with radius . Parallel cross-
sections perpendicular to the base are isosceles triangles with
height and unequal side in the base.
(a) Set up an integral for the volume of .
(b) By interpreting the integral as an area, find the volume of .
(a) Set up an integral for the volume of a solid torus (the
donut-shaped solid shown in the figure) with radii and .
(b) By interpreting the integral as an area, find the volume of
the torus.
64. Solve Example 9 taking cross-sections to be parallel to the line
of intersection of the two planes.
65. (a) Cavalieri’s Principle states that if a family of parallel planes
gives equal cross-sectional areas for two solids and ,
then the volumes of and are equal. Prove this principle.
(b) Use Cavalieri’s Principle to find the volume of the oblique
cylinder shown in the figure.
66. Find the volume common to two circular cylinders, each with
radius , if the axes of the cylinders intersect at right angles.
Find the volume common to two spheres, each with radius , if
the center of each sphere lies on the surface of the other sphere.
68. A bowl is shaped like a hemisphere with diameter 30 cm. A
ball with diameter 10 cm is placed in the bowl and water is
poured into the bowl to a depth of centimeters. Find the vol-
ume of water in the bowl.
69. A hole of radius is bored through the middle of a cylinder of
radius at right angles to the axis of the cylinder. Set up,
but do not evaluate, an integral for the volume cut out.
R ⬎ r
r
h
r
67.
r
h
r
S
2
S
1
S
2
S
1
r
R
Rr
63.
S
S
h
rS
A cap of a sphere with radius and height
52. A frustum of a pyramid with square base of side , square top
of side , and height
What happens if ? What happens if ?
53. A pyramid with height and rectangular base with dimensions
and
54. A pyramid with height and base an equilateral triangle with
side (a tetrahedron)
55. A tetrahedron with three mutually perpendicular faces and
three mutually perpendicular edges with lengths 3 cm,
4 cm, and 5 cm
56. The base of is a circular disk with radius . Parallel cross-
sections perpendicular to the base are squares.
The base of is an elliptical region with boundary curve
. Cross-sections perpendicular to the -axis
are isosceles right triangles with hypotenuse in the base.
58. The base of is the triangular region with vertices ,
, and . Cross-sections perpendicular to the -axis
are equilateral triangles.
59. The base of is the same base as in Exercise 58, but cross-
sections perpendicular to the -axis are squares.
60. The base of is the region enclosed by the parabola
and the -axis. Cross-sections perpendicular to the
-axis are squares.
61. The base of is the same base as in Exercise 60, but cross-
sections perpendicular to the -axis are isosceles triangles with
height equal to the base.
x
S
y
xy 苷 1 ⫺ x
2
S
x
S
y共0, 1兲共1, 0兲
共0, 0兲S
x9x
2
⫹ 4y
2
苷 36
S
57.
rS
a
a
a
a
h
2bb
h
a 苷 0a 苷 b
a
b
ha
b
r
h
hr
51.
SECTION 6.3 VOLUMES BY CYLINDRICAL SHELLS
||||
365
, , where is a positive con-
stant. Show that the radius of each end of the barrel is
, where .
(b) Show that the volume enclosed by the barrel is
72. Suppose that a region has area and lies above the -axis.
When is rotated about the -axis, it sweeps out a solid with
volume . When is rotated about the line (where
is a positive number), it sweeps out a solid with volume .
Express in terms of , , and .AkV
1
V
2
V
2
ky 苷 ⫺kV
1
x
xA
V 苷
1
3
h
(
2R
2
⫹ r
2
⫺
2
5
d
2
)
d 苷 ch
2
兾4r 苷 R ⫺ d
c⫺h兾2 艋 x 艋 h兾2y 苷 R ⫺ cx
2
70. A hole of radius is bored through the center of a sphere of
radius . Find the volume of the remaining portion of the
sphere.
71. Some of the pioneers of calculus, such as Kepler and Newton,
were inspired by the problem of finding the volumes of wine
barrels. (In fact Kepler published a book Stereometria doliorum
in 1715 devoted to methods for finding the volumes of barrels.)
They often approximated the shape of the sides by parabolas.
(a) A barrel with height and maximum radius is con-
structed by rotating about the -axis the parabola x
Rh
R ⬎ r
r
VOLUMES BY CYLINDRICAL SHELLS
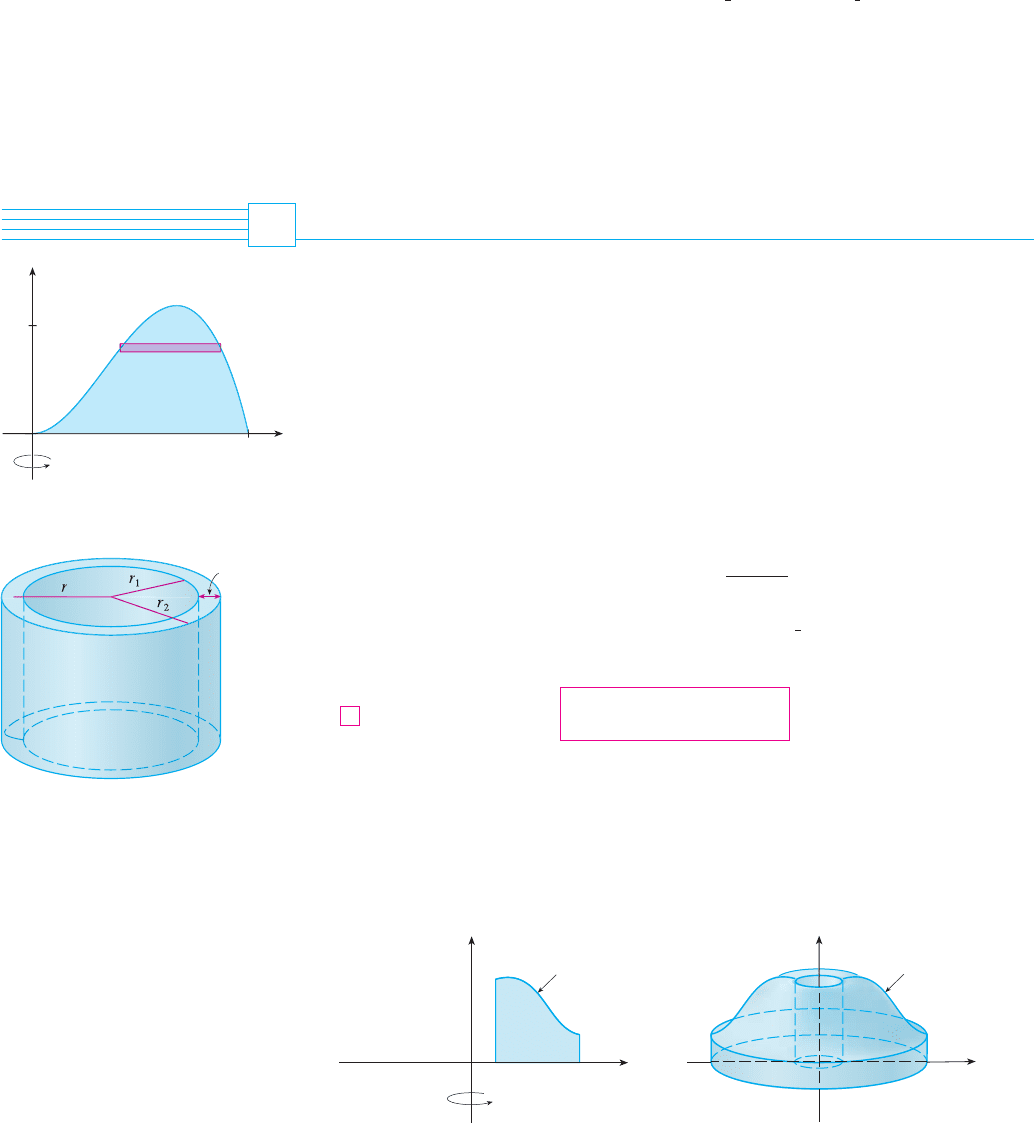
Some volume problems are very difficult to handle by the methods of the preceding sec-
tion. For instance, let’s consider the problem of finding the volume of the solid obtained
by rotating about the -axis the region bounded by and . (See Figure 1.)
If we slice perpendicular to the y-axis, we get a washer. But to compute the inner radius
and the outer radius of the washer, we would have to solve the cubic equation
for x in terms of y; that’s not easy.
Fortunately, there is a method, called the method of cylindrical shells, that is easier to
use in such a case. Figure 2 shows a cylindrical shell with inner radius , outer radius ,
and height . Its volume is calculated by subtracting the volume of the inner cylinder
from the volume of the outer cylinder:
If we let (the thickness of the shell) and (the average radius
of the shell), then this formula for the volume of a cylindrical shell becomes
and it can be remembered as
Now let be the solid obtained by rotating about the -axis the region bounded by
[where ], and , where . (See Figure 3.)
FIGURE 3
x
y
ab
0
y=ƒ
ab
x
y
0
y=ƒ
b ⬎ a 艌 0x 苷 by 苷 0, x 苷 a, f 共x兲 艌 0y 苷 f 共x兲
yS
V 苷 [circumference][height][thickness]
V 苷 2
rh ⌬r
1
r 苷
1
2
共r
2
⫹ r
1
兲⌬r 苷 r
2
⫺ r
1
苷 2
r
2
⫹ r
1
2
h共r
2
⫺ r
1
兲苷
共r
2
⫹ r
1
兲共r
2
⫺ r
1
兲h
苷
r
2
2
h ⫺
r
2
1
h 苷
共r
2
2
⫺ r
2
1
兲h V 苷 V
2
⫺ V
1
V
2
V
1
Vh
r
2
r
1
y 苷 2x
2
⫺ x
3
y 苷 0y 苷 2x
2
⫺ x
3
y
6.3
F
I
GU
RE 1
y
x
0
2
1
y=
2
≈
-
˛
x
L
x
=
?
x
R
x
=
?
F
IGURE
2
Î
r
h
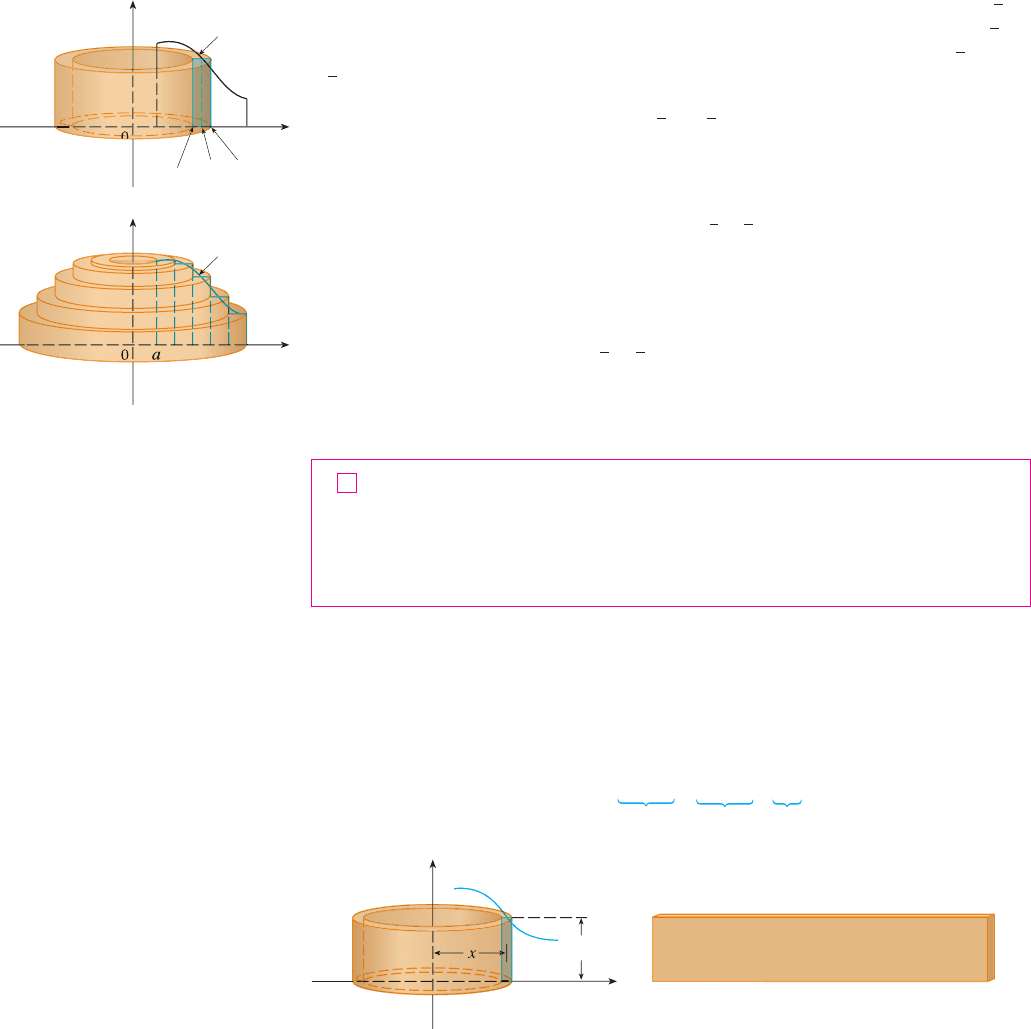
We divide the interval into n subintervals of equal width and let be
the midpoint of the ith subinterval. If the rectangle with base
and height
is
rotated about the y-axis, then the result is a cylindrical shell with average radius , height
, and thickness (see Figure 4), so by Formula 1 its volume is
Therefore an approximation to the volume of is given by the sum of the volumes of
these shells:
This approximation appears to become better as . And, from the definition of an inte-
gral, we know that
Thus the following appears plausible:
The volume of the solid in Figure 3, obtained by rotating about the y-axis the
region under the curve from a to b,is
The argument using cylindrical shells makes Formula 2 seem reasonable, but later we
will be able to prove it (see Exercise 67 in Section 8.1).
The best way to remember Formula 2 is to think of a typical shell, cut and flattened as
in Figure 5, with radius x, circumference , height , and thickness or :
This type of reasoning will be helpful in other situations, such as when we rotate about
lines other than the y-axis.
EXAMPLE 1 Find the volume of the solid obtained by rotating about the -axis the region
bounded by and .
SOLUTION
From the sketch in Figure 6 we see that a typical shell has radius x, circumfer-
ence , and height . So, by the shell method, the volume isf 共x兲 苷 2x
2
x
3
2
x
y 苷 0y 苷 2x
2
x
3
y
FI
G
URE
5
2
π
x
Î
x
ƒ
y
x
x
ƒ
thickness
height
circumference
dx关 f 共x兲兴共2
x兲
y
b
a
dxxf 共x兲2
x
where 0 a
b V 苷
y
b
a
2
xf共x兲 dx
y 苷 f 共x兲
2
lim
n
l
兺
n
i苷1
2
x
i
f 共x
i
兲 x 苷
y
b
a
2
xf共x兲 dx
n l
V ⬇
兺
n
i苷1
V
i
苷
兺
n
i苷1
2
x
i
f 共x
i
兲 x
SV
V
i
苷 共2
x
i
兲关 f 共x
i
兲兴 x
xf 共x
i
兲
x
i
f 共x
i
兲关x
i1
, x
i
兴
x
i
x关x
i1
, x
i
兴关a, b兴
366
||||
CHAPTER 6 APPLICATIONS OF INTEGRATION
FI
G
URE
4
x
y
b
y=
ƒ
x
i
–
b
a
0
0
x
y
x
i-
1
x
i
y=
ƒ
Openmirrors.com

It can be verified that the shell method gives the same answer as slicing. M
Comparing the solution of Example 1 with the remarks at the beginning of this
section, we see that the method of cylindrical shells is much easier than the washer method
for this problem. We did not have to find the coordinates of the local maximum and we did
not have to solve the equation of the curve for in terms of . However, in other examples
the methods of the preceding section may be easier.
EXAMPLE 2 Find the volume of the solid obtained by rotating about the -axis the
region between and .
SOLUTION The region and a typical shell are shown in Figure 8. We see that the shell has
radius x, circumference , and height . So the volume is
M
As the following example shows, the shell method works just as well if we rotate about
the x-axis. We simply have to draw a diagram to identify the radius and height of a shell.
EXAMPLE 3 Use cylindrical shells to find the volume of the solid obtained by rotating
about the -axis the region under the curve from 0 to 1.
SOLUTION This problem was solved using disks in Example 2 in Section 6.2. To use shells
we relabel the curve (in the figure in that example) as in Figure 9. For
rotation about the x-axis we see that a typical shell has radius y, circumference , and
height . So the volume is
In this problem the disk method was simpler.
M
苷 2
冋
y
2
2
y
4
4
册
0
1
苷
2
V 苷
y
1
0
共2
y兲共1 y
2
兲 dy 苷 2
y
1
0
共y y
3
兲 dy
1 y
2
2
y
x 苷 y
2
y 苷
s
x
y 苷
s
x
x
V
苷 2
冋
x
3
3
x
4
4
册
0
1
苷
6
V 苷
y
1
0
共2
x兲共x x
2
兲 dx 苷 2
y
1
0
共x
2
x
3
兲 dx
x x
2
2
x
y 苷 x
2
y 苷 x
y
V
yx
NOTE
FIGURE 7
y
x
苷 2
[
1
2
x
4
1
5
x
5
]
0
2
苷 2
(
8
32
5
)
苷
16
5
V 苷
y
2
0
共2
x兲共2x
2
x
3
兲 dx 苷 2
y
2
0
共2x
3
x
4
兲 dx
SECTION 6.3 VOLUMES BY CYLINDRICAL SHELLS
||||
367
FI
GU
RE
6
y
x
2
≈
-
˛
x
2
N Figure 7 shows a computer-generated
picture of the solid whose volume we computed
in Example 1.
F
I
GU
RE
9
1
y
y
sh
e
ll
r
adius
=y
s
hell hei
g
h
t
=1-
¥
0
x
x
=
1
1
x=
=
¥
¥
¥
¥
F
I
GU
RE
8
0
x
y
y
=
x
y
=
≈
x
shel
l
h
e
i
g
ht
=
x-
≈

EXAMPLE 4 Find the volume of the solid obtained by rotating the region bounded by
and about the line .
SOLUTION Figure 10 shows the region and a cylindrical shell formed by rotation about the
line . It has radius , circumference , and height .
The volume of the given solid is
M
苷 2
冋
x
4
4
x
3
x
2
册
0
1
苷
2
V 苷
y
1
0
2
共2 x兲共x x
2
兲 dx 苷 2
y
1
0
共x
3
3x
2
2x兲 dx
FIGURE 10
0
y
x
y=x-≈
0
y
x
x
1 2 3 4
2-x
x=2
x x
2
2
共2 x兲2 xx 苷 2
x 苷 2y 苷 0y 苷 x x
2
V
368
||||
CHAPTER 6 APPLICATIONS OF INTEGRATION
4. ,,
5. ,,,
6. ,
7. ,
8. Let be the volume of the solid obtained by rotating about the
-axis the region bounded by and . Find both
by slicing and by cylindrical shells. In both cases draw a dia-
gram to explain your method.
9–14 Use the method of cylindrical shells to find the volume of the
solid obtained by rotating the region bounded by the given curves
about the -axis. Sketch the region and a typical shell.
9.
10.
11.
,,
12. ,
,
14.
15–20 Use the method of cylindrical shells to find the volume gen-
erated by rotating the region bounded by the given curves about the
specified axis. Sketch the region and a typical shell.
15. , ; about x 苷 2y 苷 0, x 苷 1y 苷 x
4
x y 苷 3, x 苷 4 共y 1兲
2
x 苷 2x 苷 1 共y 2兲
2
13.
x 苷 0x 苷 4y
2
y
3
x 苷 0y 苷 8y 苷 x
3
x 苷
s
y
, x 苷 0, y 苷 1
x 苷 1 y
2
, x 苷 0, y 苷 1, y 苷 2
x
Vy 苷 x
2
y 苷
s
x
y
V
y 苷 x
2
4x 7y 苷 4共x 2兲
2
x y 苷 3y 苷 3 2x x
2
x 苷 0y 苷 40 x 2y 苷 x
2
x 苷 1y 苷 0y 苷 x
2
1. Let be the solid obtained by rotating the region shown in
the figure about the -axis. Explain why it is awkward to use
slicing to find the volume of . Sketch a typical approxi-
mating shell. What are its circumference and height? Use shells
to find .
2. Let be the solid obtained by rotating the region shown in the
figure about the -axis. Sketch a typical cylindrical shell and
find its circumference and height. Use shells to find the volume
of . Do you think this method is preferable to slicing? Explain.
3–7 Use the method of cylindrical shells to find the volume gener-
ated by rotating the region bounded by the given curves about the
-axis. Sketch the region and a typical shell.
3. ,,,x 苷 2x 苷 1y 苷 0y 苷 1兾x
y
0
x
y
œ
„
π
y=sin{≈}
S
y
S
0
x
y
1
y=x(x-1)@
V
SV
y
S
EXERCISES
6.3
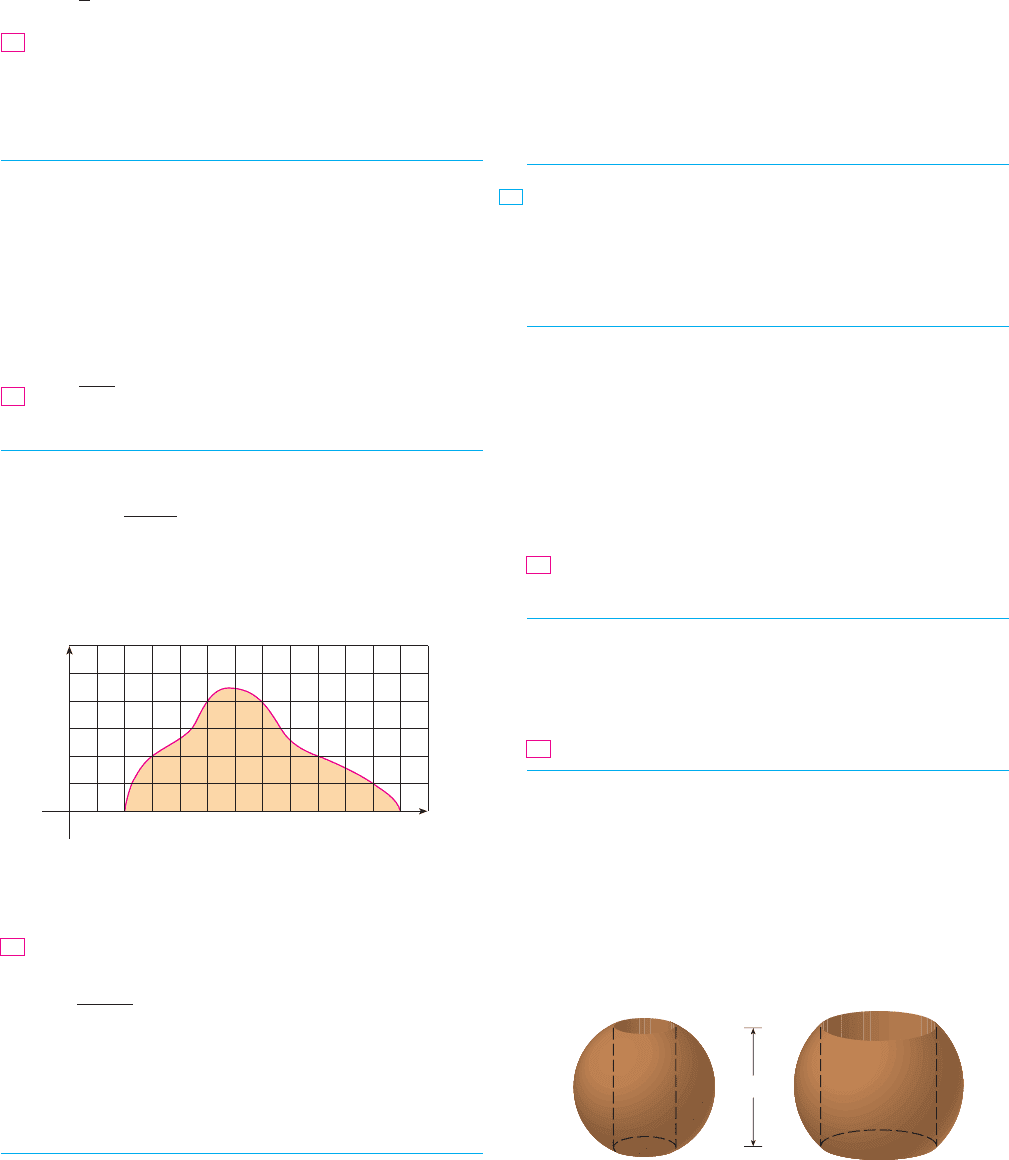
;
33–34 Use a graph to estimate the -coordinates of the points of
intersection of the given curves. Then use this information and
your calculator to estimate the volume of the solid obtained by
rotating about the -axis the region enclosed by these curves.
33. ,
34. ,
35–36 Use a computer algebra system to find the exact volume
of the solid obtained by rotating the region bounded by the given
curves about the specified line.
35. , , ; about
36. , , ; about
37– 42 The region bounded by the given curves is rotated about
the specified axis. Find the volume of the resulting solid by any
method.
37. , ; about the -axis
38. , ; about the -axis
39. , ; about
40. , ; about
; about the -axis
42. , ; about
43– 45 Use cylindrical shells to find the volume of the solid.
43. A sphere of radius
44. The solid torus of Exercise 63 in Section 6.2
A right circular cone with height and base radius
46. Suppose you make napkin rings by drilling holes with differ-
ent diameters through two wooden balls (which also have dif-
ferent diameters). You discover that both napkin rings have
the same height , as shown in the figure.
(a) Guess which ring has more wood in it.
(b) Check your guess: Use cylindrical shells to compute the
volume of a napkin ring created by drilling a hole with
radius through the center of a sphere of radius and
express the answer in terms of .
h
h
Rr
h
rh
45.
r
y 苷 1x 苷 4x 苷 共y 3兲
2
yx
2
共y 1兲
2
苷 1
41.
x 苷 2x 苷 0x 苷 1 y
4
x 苷 1y 苷 x
2
5x 9y 苷 5
xy 苷 0y 苷 x
2
6x 8
yy 苷 0y 苷 x
2
6x 8
x 苷 10 x
y 苷 0y 苷 x
3
sin x
x 苷
兾20 x
y 苷 sin
4
xy 苷 sin
2
x
CAS
y 苷 x
4
4x 1y 苷 x
3
x 1
y 苷 x x
2
x
4
y 苷 0
y
x
16. , ; about
, ; about
18. , ; about
19. , , ; about
20.
21– 26 Set up, but do not evaluate, an integral for the volume
of the solid obtained by rotating the region bounded by the given
curves about the specified axis.
21. , , , ; about the -axis
22. , ; about
23. , ; about
24. about
about
26. about
27. Use the Midpoint Rule with to estimate the volume
obtained by rotating about the -axis the region under the
curve , .
28. If the region shown in the figure is rotated about the -axis to
form a solid, use the Midpoint Rule with to estimate
the volume of the solid.
29–32 Each integral represents the volume of a solid. Describe
the solid.
30.
31.
32.
y
兾4
0
2
共
x兲共cos x sin x兲 dx
y
1
0
2
共3 y兲共1 y
2
兲 dy
2
y
2
0
y
1 y
2
dy
y
3
0
2
x
5
dx
29.
0
x
y
1
1
2
3
4
5
23456789101112
n 苷 5
y
0 x 1y 苷
s
1 x
3
y
n 苷 5
y 苷 5x
2
y
2
苷 7, x 苷 4;
y 苷 4x 苷
s
sin y
,0 y
, x 苷 0;
25.
x 苷 2y 苷 1兾共1 x
2
兲, y 苷 0, x 苷 0, x 苷 2;
x 苷 1y 苷 sin共
x兾2兲y 苷 x
4
x 苷 7y 苷 4x x
2
y 苷 x
yx 苷 3
x 苷 2
y 苷 0y 苷 sin x
y 苷 x
2
, x 苷 y
2
; about y 苷 1
y 苷 1x 苷 1y 苷 0y 苷 x
3
x 苷 1y 苷 2 x
2
y 苷 x
2
x 苷 1y 苷 3y 苷 4x x
2
17.
x 苷 1y 苷 0, x 苷 1y 苷
s
x
SECTION 6.3 VOLUMES BY CYLINDRICAL SHELLS
||||
369
WORK
The term work is used in everyday language to mean the total amount of effort required to
perform a task. In physics it has a technical meaning that depends on the idea of a force.
Intuitively, you can think of a force as describing a push or pull on an object—for example,
a horizontal push of a book across a table or the downward pull of the earth’s gravity on a
ball. In general, if an object moves along a straight line with position function , then
the force F on the object (in the same direction) is defined by Newton’s Second Law of
Motion as the product of its mass and its acceleration:
In the SI metric system, the mass is measured in kilograms (kg), the displacement in
meters (m), the time in seconds (s), and the force in newtons ( ). Thus a force
of 1 N acting on a mass of 1 kg produces an acceleration of 1 m兾s . In the US Customary
system, the fundamental unit is chosen to be the unit of force, which is the pound.
In the case of constant acceleration, the force is also constant and the work done is
defined to be the product of the force and the distance that the object moves:
If is measured in newtons and in meters, then the unit for is a newton-meter, which
is called a joule (J). If is measured in pounds and in feet, then the unit for is a foot-
pound (ft-lb), which is about 1.36 J.
EXAMPLE 1
(a) How much work is done in lifting a 1.2-kg book off the floor to put it on a desk that
is 0.7 m high? Use the fact that the acceleration due to gravity is m兾s.
(b) How much work is done in lifting a 20-lb weight 6 ft off the ground?
SOLUTION
(a) The force exerted is equal and opposite to that exerted by gravity, so Equation 1
gives
and then Equation 2 gives the work done as
(b) Here the force is given as lb, so the work done is
Notice that in part (b), unlike part (a), we did not have to multiply by because we
were given the weight (which is a force) and not the mass of the object. M
Equation 2 defines work as long as the force is constant, but what happens if the force
is variable? Let’s suppose that the object moves along the -axis in the positive direction,
from to , and at each point between and a force acts on the object,
where is a continuous function. We divide the interval into n subintervals with end-
points and equal width . We choose a sample point in the th sub-
interval . Then the force at that point is . If is large, then is small, and xnf 共x
i
*
兲关x
i1
, x
i
兴
ix
i
*
xx
0
, x
1
, ..., x
n
关a, b兴f
f 共x兲baxx 苷 bx 苷 a
x
t
W 苷 Fd 苷 20 ⴢ 6 苷 120 ft-lb
F 苷 20
W 苷 Fd 苷 共11.76兲共0.7兲⬇8.2 J
F 苷 mt 苷 共1.2兲共9.8兲 苷 11.76 N
2
t 苷 9.8
V
WdF
WdF
work 苷 force distanceW 苷 Fd
2
dF
F
2
N 苷 kgm兾s
2
F 苷 m
d
2
s
dt
2
1
m
s共t兲
6.4
370
||||
CHAPTER 6 APPLICATIONS OF INTEGRATION
since is continuous, the values of don’t change very much over the interval .
In other words, is almost constant on the interval and so the work that is done in mov-
ing the particle from to is approximately given by Equation 2:
Thus we can approximate the total work by
It seems that this approximation becomes better as we make larger. Therefore we define
the work done in moving the object from a to b as the limit of this quantity as .
Since the right side of (3) is a Riemann sum, we recognize its limit as being a definite inte-
gral and so
EXAMPLE 2 When a particle is located a distance feet from the origin, a force of
pounds acts on it. How much work is done in moving it from to ?
SOLUTION
The work done is ft-lb. M
In the next example we use a law from physics: Hooke’s Law states that the force
required to maintain a spring stretched units beyond its natural length is proportional
to :
where is a positive constant (called the spring constant). Hooke’s Law holds provided
that is not too large (see Figure 1).
EXAMPLE 3 A force of 40 N is required to hold a spring that has been stretched from
its natural length of 10 cm to a length of 15 cm. How much work is done in stretching
the spring from 15 cm to 18 cm?
SOLUTION According to Hooke’s Law, the force required to hold the spring stretched
meters beyond its natural length is . When the spring is stretched from 10 cm
to 15 cm, the amount stretched is cm m. This means that , so
Thus and the work done in stretching the spring from 15 cm to 18 cm is
M
苷 400关共0.08兲
2
共0.05兲
2
兴 苷 1.56 J
W 苷
y
0.08
0.05
800xdx苷 800
x
2
2
册
0.05
0.08
f 共x兲 苷 800x
k 苷
40
0.05
苷 8000.05k 苷 40
f 共0.05兲 苷 40苷 0.055
f 共x兲 苷 kxx
V
x
k
f 共x兲 苷 kx
x
x
16
2
3
W 苷
y
3
1
共x
2
2x兲 dx 苷
x
3
3
x
2
册
1
3
苷
50
3
x 苷 3x 苷 1x
2
2x
x
W 苷 lim
n l
兺
n
i苷1
f 共x
i
*
兲 x 苷
y
b
a
f 共x兲 dx
4
n l
n
W ⬇
兺
n
i苷1
f 共x
i
*
兲 x
3
W
i
⬇ f 共x
i
*
兲 x
x
i
x
i1
W
i
f
关x
i1
, x
i
兴ff
SECTION 6.4 WORK
||||
371
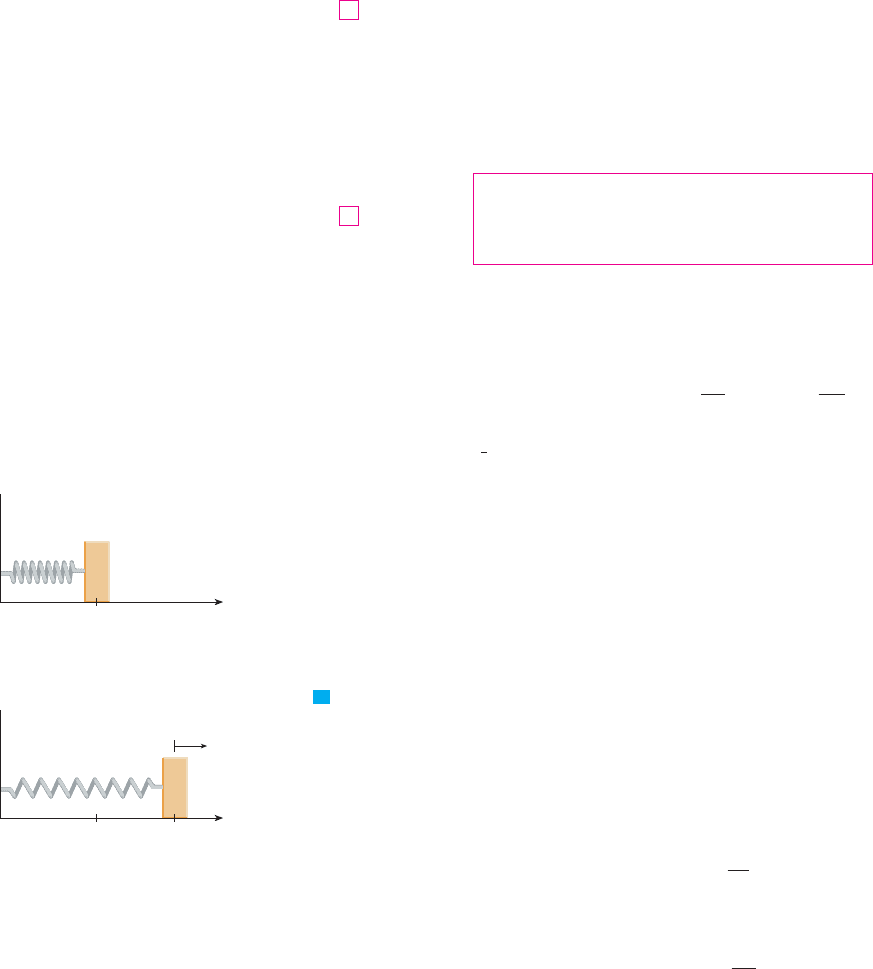
FIGURE 1
Hooke’s Law
x
0
frictionless
surface
x
0 x
ƒ=kx
(a) Natural position of spring
(b) Stretched position of spring
