Stewart J. Calculus

Подождите немного. Документ загружается.

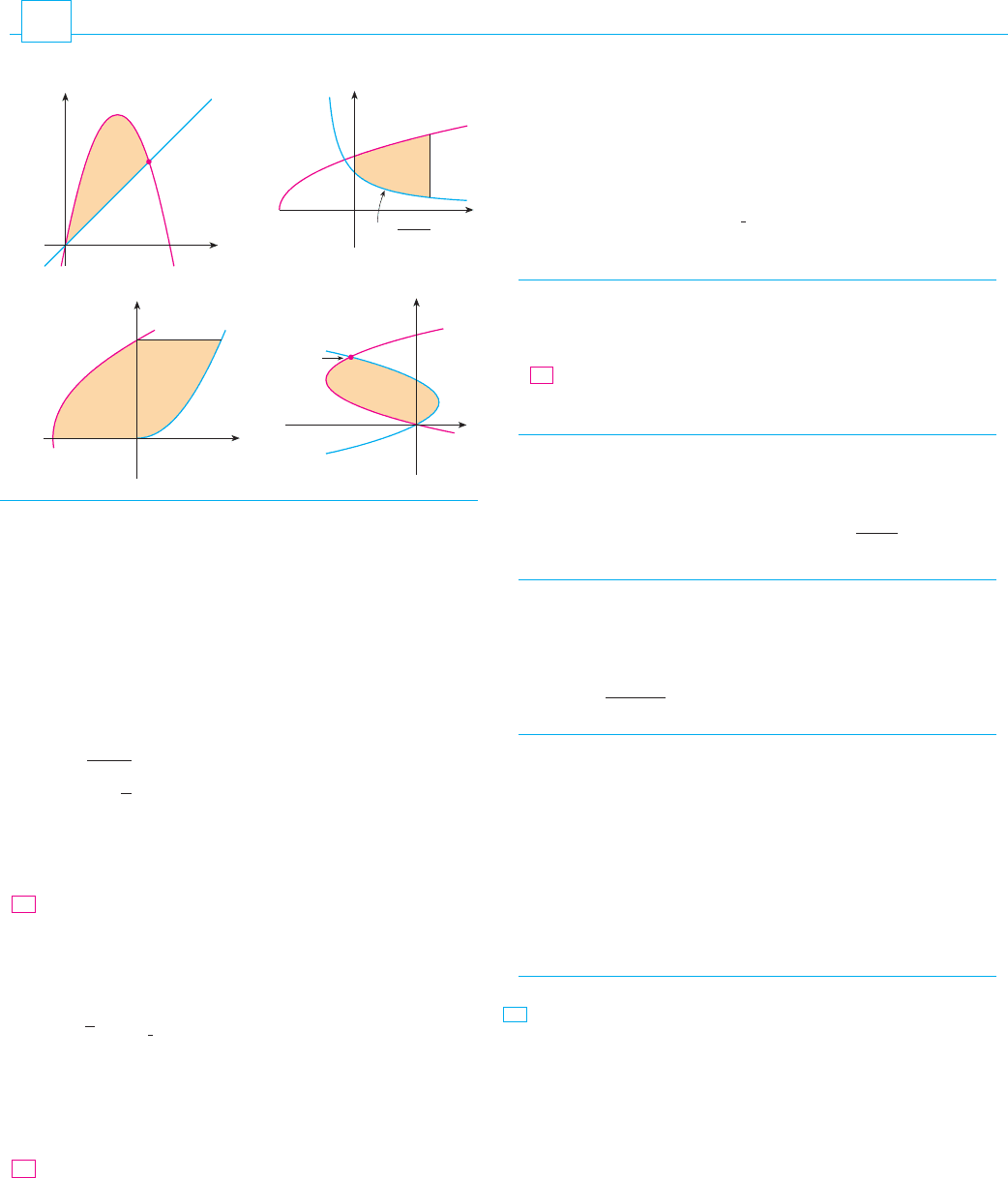
352

||||

CHAPTER 6 APPLICATIONS OF INTEGRATION

22. ,

23. ,,,

24. ,,

25.

26.

27.

28. ,, ,

29–30 Use calculus to ﬁnd the area of the triangle with the given

vertices.

30. ,,

31–32 Evaluate the integral and interpret it as the area of a

region. Sketch the region.

31. 32.

33–34 Use the Midpoint Rule with to approximate the

area of the region bounded by the given curves.

33. ,,

34. ,,

;

35–38 Use a graph to ﬁnd approximate -coordinates of the points

of intersection of the given curves. Then ﬁnd (approximately) the

area of the region bounded by the curves.

35. ,

36. ,

37. ,

38. ,

39. Use a computer algebra system to ﬁnd the exact area

enclosed by the curves and .

40. Sketch the region in the -plane deﬁned by the inequalities

, and ﬁnd its area.

41. Racing cars driven by Chris and Kelly are side by side at the

start of a race. The table shows the velocities of each car (in

miles per hour) during the ﬁrst ten seconds of the race. Use

1 ⫺ x ⫺

ⱍ

艌 0x ⫺ 2y

艌 0

y 苷 xy 苷 x

⫺ 6x

⫹ 4x

CAS

y 苷 x

y 苷 x cos x

y 苷 x

⫺ 3x ⫹ 4y 苷 3x

⫺ 2x

y 苷 3x ⫺ x

y 苷 x

y 苷 x sin共x

兲

x 苷 0y 苷 xy 苷

16 ⫺ x

0 艋 x 艋 1y 苷 cos

共

␲

x兾4兲y 苷 sin

共

␲

x兾4兲

n 苷 4

ⱍ

x ⫹ 2

⫺ x

ⱍ

␲

兾2

ⱍ

sin x ⫺ cos 2x

ⱍ

共5, 1兲共2, ⫺2兲共0, 5兲

共⫺1, 6兲共2, 1兲共0, 0兲

29.

x 艌 04x ⫹ y 苷 4y 苷 8x

y 苷 3x

y 苷

xy 苷 xy 苷 1兾x

y 苷

ⱍ

, y 苷 x

⫺ 2

y 苷 cos x, y 苷 1 ⫺ 2x兾

␲

0 艋 x 艋

␲

y 苷 1 ⫺ cos xy 苷 cos x

x 苷

␲

兾2x 苷 0y 苷 sin 2xy 苷 cos x

y 苷 xy 苷 sin共

␲

x兾2兲

1– 4 Find the area of the shaded region.

1. 2.

3. 4.

5–28 Sketch the region enclosed by the given curves. Decide

whether to integrate with respect to x or y. Draw a typical approx-

imating rectangle and label its height and width. Then ﬁnd the

area of the region.

10.

11.

12. ,

14. ,,

15. ,,

16.

17.

18. ,, ,

19. ,

20. ,

, x 苷 y

⫺ 1x 苷 1 ⫺ y

21.

x 苷 y4x ⫹ y

苷 12

x 苷 4 ⫹ y

x 苷 2y

x 苷 3x 苷 ⫺3y 苷 x

y 苷 8 ⫺ x

x 苷 9y 苷

xy 苷

y 苷 x

⫺ x, y 苷 3x

⫺

␲

兾3 艋 x 艋

␲

兾3y 苷 8 cos xy 苷 sec

0 艋 x 艋 2

␲

y 苷 2 ⫺ cos xy 苷 cos x

y 苷 x

⫺ 6y 苷 12 ⫺ x

13.

y 苷 4x ⫺ x

y 苷 x

苷 xy 苷 x

y 苷 1 ⫹

, y 苷共3 ⫹ x兲兾3

y 苷

x ⫹ 3

, y 苷共x ⫹ 3兲兾2

y 苷 x

⫺ 2x, y 苷 x ⫹ 4

y 苷 x

y 苷 sin x, y 苷 x, x 苷

␲

兾2, x 苷

␲

y 苷 x ⫹ 1, y 苷 9 ⫺ x

, x 苷 ⫺1, x 苷 2

(_3,3)

x=2y-¥

x=¥-4y

y=1

x=¥-1

x=œ

„y

x=2

y=œ

„„„„

x+2

x+1

y=x

y=5x-≈

(4,4)

EXERCISES

6.1

SECTION 6.1 AREAS BETWEEN CURVES

||||

353

46. The ﬁgure shows graphs of the marginal revenue function

and the marginal cost function for a manufacturer. [Recall

from Section 4.7 that and represent the revenue and

cost when units are manufactured. Assume that and are

measured in thousands of dollars.] What is the meaning of the

area of the shaded region? Use the Midpoint Rule to estimate

the value of this quantity.

;

47. The curve with equation is called Tschirn-

hausen’s cubic. If you graph this curve you will see that part

of the curve forms a loop. Find the area enclosed by the loop.

48. Find the area of the region bounded by the parabola ,

the tangent line to this parabola at , and the -axis.

49. Find the number such that the line divides the region

bounded by the curves and into two regions

with equal area.

50. (a) Find the number such that the line bisects the

area under the curve ,

(b) Find the number such that the line bisects the

area in part (a).

Find the values of such that the area of the region bounded

by the parabolas and is 576.

52. Suppose that . For what value of is the area of

the region enclosed by the curves , ,

and equal to the area of the region enclosed by the

curves , , and ?

The following exercises are intended only for those who have

already covered Chapter 7.

53–55 Sketch the region bounded by the given curves and ﬁnd

the area of the region.

54.

55. ,,

For what values of do the line and the curve

enclose a region? Find the area of the region.y 苷 x兾共x

⫹ 1兲

y 苷 mxm

56.

⫺

␲

兾3 艋 x 艋

␲

兾3y 苷 2 sin xy 苷 tan x

y 苷 sin x, y 苷 e

, x 苷 0, x 苷

␲

兾2

y 苷 1兾x, y 苷 1兾x

, x 苷 2

53.

y 苷 0x 苷

␲

y 苷 cos共x ⫺ c兲

x 苷 0

y 苷 cos共x ⫺ c兲y 苷 cos x

⬍

␲

兾2

y 苷 c

⫺ x

y 苷 x

⫺ c

51.

y 苷 bb

1 艋 x 艋 4.y 苷 1兾x

x 苷 aa

y 苷 4y 苷 x

y 苷 bb

x共1, 1兲

y 苷 x

苷 x

共x ⫹ 3兲

Cª(x)

10050

Rª(x)

CRx

C共x兲R共x兲

C⬘

R⬘

the Midpoint Rule to estimate how much farther Kelly travels

than Chris does during the ﬁrst ten seconds.

42. The widths (in meters) of a kidney-shaped swimming pool

were measured at 2-meter intervals as indicated in the ﬁgure.

Use the Midpoint Rule to estimate the area of the pool.

43. A cross-section of an airplane wing is shown. Measurements

of the thickness of the wing, in centimeters, at 20-centimeter

intervals are ,,,,,,,,,

, and . Use the Midpoint Rule to estimate the area of

the wing’s cross-section.

44. If the birth rate of a population is

people per year and the death

rate is people per year, ﬁnd the area

between these curves for . What does this area

represent?

Two cars, A and B, start side by side and accelerate from rest.

The ﬁgure shows the graphs of their velocity functions.

(a) Which car is ahead after one minute? Explain.

(b) What is the meaning of the area of the shaded region?

(d) Estimate the time at which the cars are again side by side.

√

t (min)

45.

0 艋 t 艋 10

d共t兲苷 1460 ⫹ 28.8t

b共t兲苷 2200 ⫹ 52.3t ⫹ 0.74t

200 cm

2.88.7

15.120.523.827.327.629.026.720.35.8

6.2

5.0

7. 2

6.8

5.6

4.8

0 0 0 6 69 80

20 22 7 75 86

32 37 8 81 93

46 52 9 86 98

54 61 10 90 102

56271

VOLUMES

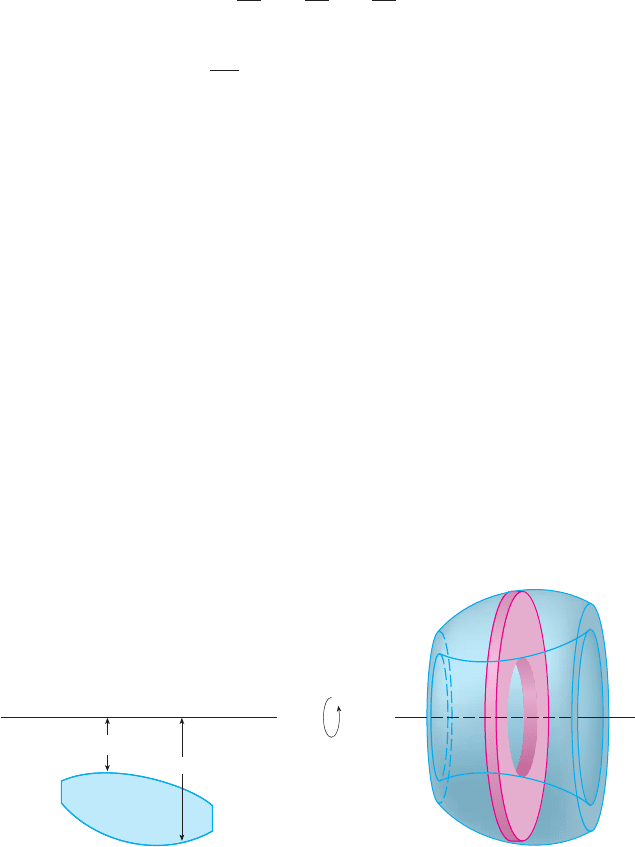
In trying to ﬁnd the volume of a solid we face the same type of problem as in ﬁnding areas.

We have an intuitive idea of what volume means, but we must make this idea precise by

using calculus to give an exact deﬁnition of volume.

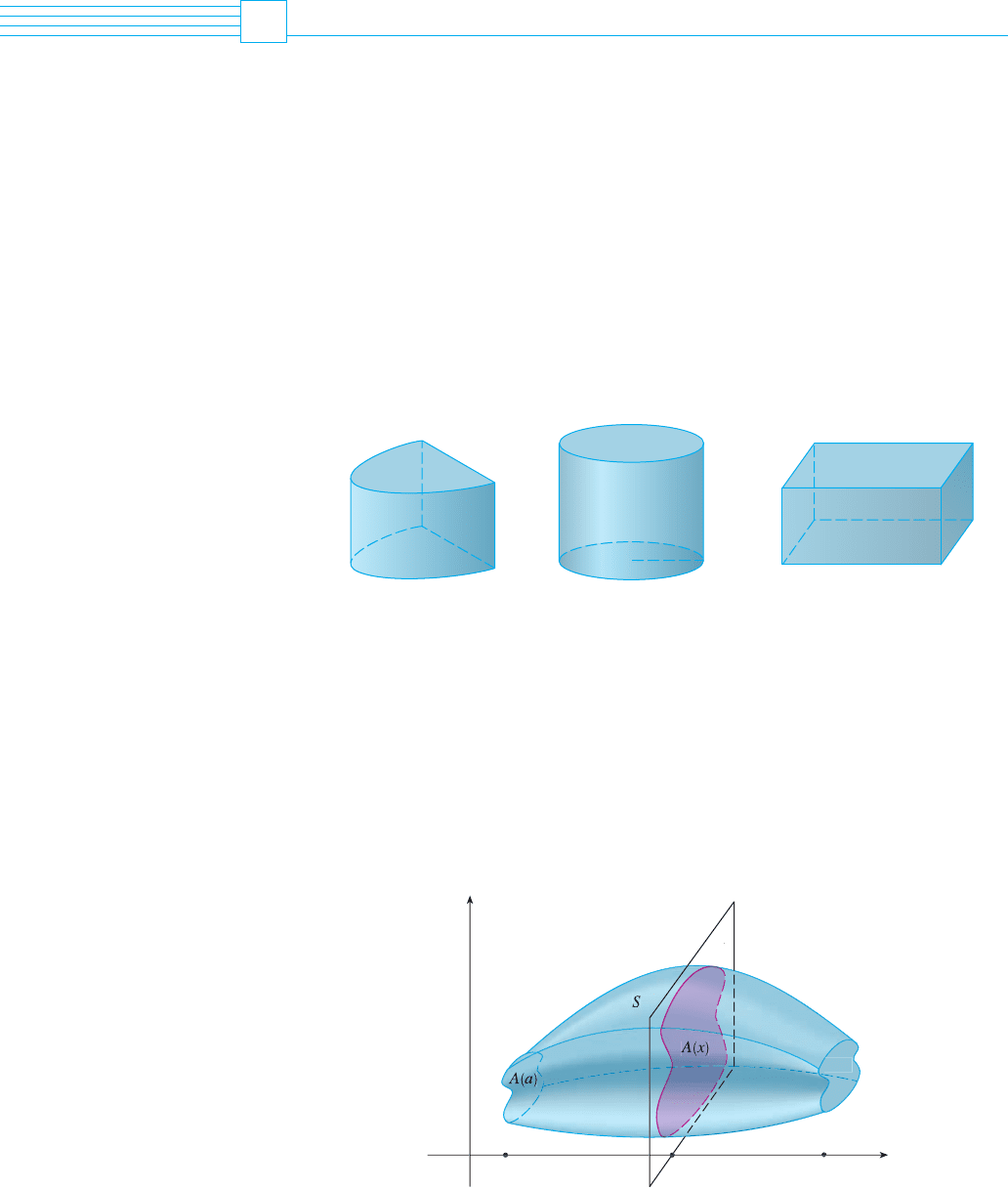
We start with a simple type of solid called a cylinder (or, more precisely, a right cylin-

der). As illustrated in Figure 1(a), a cylinder is bounded by a plane region , called the

base, and a congruent region in a parallel plane. The cylinder consists of all points on

line segments that are perpendicular to the base and join to . If the area of the base is

and the height of the cylinder (the distance from to ) is , then the volume of the

cylinder is deﬁned as

In particular, if the base is a circle with radius , then the cylinder is a circular cylinder with

volume [see Figure 1(b)], and if the base is a rectangle with length and width

, then the cylinder is a rectangular box (also called a rectangular parallelepiped) with

volume [see Figure 1(c)].

For a solid S that isn’t a cylinder we ﬁrst “cut” S into pieces and approximate each piece

by a cylinder. We estimate the volume of S by adding the volumes of the cylinders. We

arrive at the exact volume of S through a limiting process in which the number of pieces

becomes large.

We start by intersecting S with a plane and obtaining a plane region that is called a

cross-section of Let be the area of the cross-section of in a plane perpen-

dicular to the -axis and passing through the point , where . (See Figure 2.

Think of slicing with a knife through and computing the area of this slice.) The cross-

sectional area will vary as increases from to .

URE

A(b)

baxA共x兲

a 艋 x 艋 bxx

SA共x兲S.

FIGURE 1

B¡

B™

(a) Cylinder

V=Ah

(b) Circular cylinder

V=πr@h

V=lwh

V 苷 lwh

lV 苷

␲

V 苷 Ah

VhB

6.2

354

||||

CHAPTER 6 APPLICATIONS OF INTEGRATION

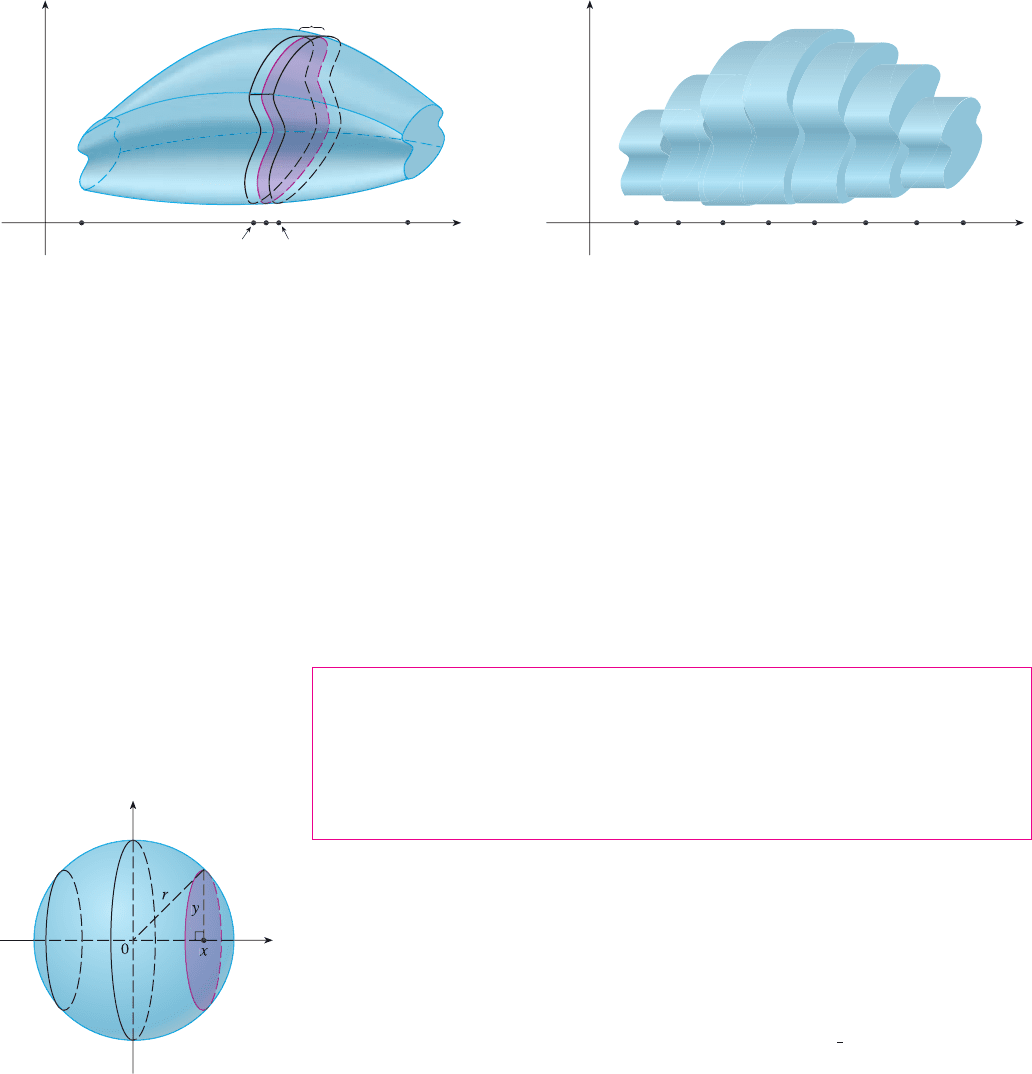
Let’s divide S into n “slabs” of equal width by using the planes , ,...to slice

the solid. (Think of slicing a loaf of bread.) If we choose sample points in , we

can approximate the th slab (the part of that lies between the planes and ) by

a cylinder with base area and “height” . (See Figure 3.)

FIGURE 3

The volume of this cylinder is , so an approximation to our intuitive concep-

tion of the volume of the th slab is

Adding the volumes of these slabs, we get an approximation to the total volume (that is,

what we think of intuitively as the volume):

This approximation appears to become better and better as . (Think of the slices as

becoming thinner and thinner.) Therefore, we deﬁne the volume as the limit of these sums

as . But we recognize the limit of Riemann sums as a deﬁnite integral and so we

have the following deﬁnition.

DEFINITION OF VOLUME Let be a solid that lies between and . If the

cross-sectional area of in the plane , through x and perpendicular to the x-axis,

is , where is a continuous function, then the volume of is

When we use the volume formula , it is important to remember that

is the area of a moving cross-section obtained by slicing through perpendicular to

the -axis.

Notice that, for a cylinder, the cross-sectional area is constant: for all . So our

deﬁnition of volume gives ; this agrees with the formula

EXAMPLE 1 Show that the volume of a sphere of radius is .

SOLUTION If we place the sphere so that its center is at the origin (see Figure 4), then the

plane intersects the sphere in a circle whose radius (from the Pythagorean Theorem) P

V 苷

␲

V 苷 Ah.V 苷 x

A dx 苷 A共b ⫺ a兲

xA共x兲苷 A

xA共x兲

V 苷 x

A共x兲 dx

V 苷 lim

⬁

兺

i苷1

A共x

兲 ⌬x 苷

A共x兲 dx

SAA共x兲

x 苷 bx 苷 aS

n l ⬁

V ⬇

兺

i苷1

A共x

兲 ⌬x

V共S

兲⬇A共x

兲 ⌬x

A共x

兲 ⌬x

⁄¤

‹

∞

i-1

Îx

⌬xA共x

兲

i⫺1

关x

i⫺1

, x

兴x

⌬x

SECTION 6.2 VOLUMES

||||

355

N It can be proved that this deﬁnition is inde-

pendent of how is situated with respect to

the -axis. In other words, no matter how we

slice with parallel planes, we always get the

same answer for .V

. So the cross-sectional area is

Using the deﬁnition of volume with and , we have

(The integrand is even.)

Figure 5 illustrates the deﬁnition of volume when the solid is a sphere with radius

. From the result of Example 1, we know that the volume of the sphere is

. Here the slabs are circular cylinders, or disks, and the three parts of Fig-

ure 5 show the geometric interpretations of the Riemann sums

when n 苷 5, 10, and 20 if we choose the sample points to be the midpoints . Notice

that as we increase the number of approximating cylinders, the corresponding Riemann

sums become closer to the true volume.

EXAMPLE 2 Find the volume of the solid obtained by rotating about the x-axis the

region under the curve from 0 to 1. Illustrate the deﬁnition of volume by sketch-

ing a typical approximating cylinder.

SOLUTION The region is shown in Figure 6(a). If we rotate about the x-axis, we get the

solid shown in Figure 6(b). When we slice through the point x, we get a disk with radius

. The area of this cross-section is

and the volume of the approximating cylinder (a disk with thickness ) is

A共x兲 ⌬x 苷

␲

x ⌬x

⌬x

A共x兲苷

␲

(

)

苷

␲

y 苷

(a) Using 5 disks, VÅ4.2726 (b) Using 10 disks, VÅ4.2097 (c) Using 20 disks, VÅ4.1940

FIGURE 5

Approximating the volume of a sphere with radius 1

兺

i苷1

A共x

兲 ⌬x 苷

兺

i苷1

␲

共1

⫺ x

兲 ⌬x

␲

⬇ 4.18879

r 苷 1

苷

␲

苷 2

␲

冋

x ⫺

册

苷 2

␲

冉

⫺

冊

苷 2

␲

共r

⫺ x

兲 dx

V 苷

⫺r

A共x兲 dx 苷

⫺r

␲

共r

⫺ x

兲 dx

b 苷 ra 苷 ⫺r

A共x兲苷

␲

苷

␲

共r

⫺ x

兲

y 苷

⫺ x

356

||||

CHAPTER 6 APPLICATIONS OF INTEGRATION

Visual 6.2A shows an animation

of Figure 5.

TEC

The solid lies between and , so its volume is

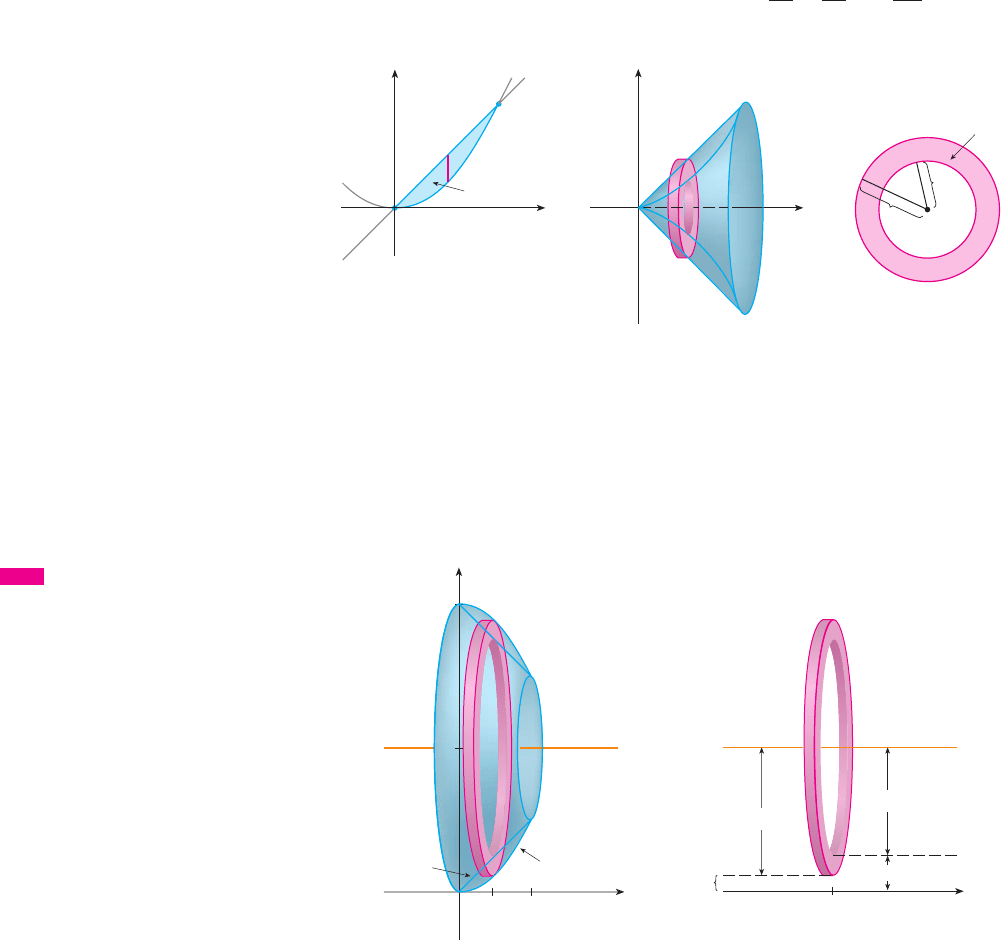
EXAMPLE 3 Find the volume of the solid obtained by rotating the region bounded by

, , and about the -axis.

SOLUTION The region is shown in Figure 7(a) and the resulting solid is shown in

Figure 7(b). Because the region is rotated about the y-axis, it makes sense to slice the

solid perpendicular to the y-axis and therefore to integrate with respect to y. If we slice

at height y, we get a circular disk with radius x, where . So the area of a cross-

section through y is

and the volume of the approximating cylinder pictured in Figure 7(b) is

Since the solid lies between y 苷 0 and y 苷 8, its volume is

(

)

(

x,y

)

(

)

œ„

苷

␲

[

5兾3

]

苷

␲

V 苷

A共y兲 dy 苷

␲

2兾3

A共y兲 ⌬y 苷

␲

2兾3

⌬y

A共y兲苷

␲

苷

␲

(

)

苷

␲

2兾3

x 苷

yx 苷 0y 苷 8y 苷 x

FIGURE

(

)

œ„

(

)

V 苷

A共x兲 dx 苷

␲

xdx苷

␲

册

苷

␲

x 苷 1x 苷 0

SECTION 6.2 VOLUMES

||||

357

N Did we get a reasonable answer in

Example 2? As a check on our work, let’s

replace the given region by a square with base

and height . If we rotate this square,

we get a cylinder with radius , height , and

volume . We computed that the

given solid has half this volume. That seems

about right.

␲

ⴢ 1

ⴢ 1 苷

␲

1关0, 1兴

EXAMPLE 4 The region enclosed by the curves and is rotated about the

-axis. Find the volume of the resulting solid.

SOLUTION The curves and intersect at the points and . The region

between them, the solid of rotation, and a cross-section perpendicular to the -axis are

shown in Figure 8. A cross-section in the plane has the shape of a washer (an annular

ring) with inner radius and outer radius , so we ﬁnd the cross-sectional area by sub-

tracting the area of the inner circle from the area of the outer circle:

Therefore we have

EXAMPLE 5 Find the volume of the solid obtained by rotating the region in Example 4

about the line .

SOLUTION The solid and a cross-section are shown in Figure 9. Again the cross-section is

a washer, but this time the inner radius is and the outer radius is .

FIGURE 9

y=2

y=≈

y=x

2-≈

≈

2-x

2 ⫺ x

y 苷 2

FIGURE 8

(1,1)

y=≈

y=x

᏾

(b)

(a)

(c)

≈

A(x)

(0, 0)

苷

␲

冋

⫺

册

苷

␲

V 苷

A共x兲 dx 苷

␲

共x

⫺ x

兲 dx

A共x兲苷

␲

⫺

␲

共x

兲

苷

␲

共x

⫺ x

兲

共1, 1兲共0, 0兲y 苷 x

y 苷 x

y 苷 x᏾

358

||||

CHAPTER 6 APPLICATIONS OF INTEGRATION

Visual 6.2B shows how solids of

revolution are formed.

TEC

The cross-sectional area is

and so the volume of is

The solids in Examples 1–5 are all called solids of revolution because they are obtained

by revolving a region about a line. In general, we calculate the volume of a solid of revo-

lution by using the basic deﬁning formula

and we ﬁnd the cross-sectional area or in one of the following ways:

If the cross-section is a disk (as in Examples 1–3), we ﬁnd the radius of the disk

(in terms of x or y) and use

If the cross-section is a washer (as in Examples 4 and 5), we ﬁnd the inner

radius and outer radius from a sketch (as in Figures 8, 9, and 10) and

compute the area of the washer by subtracting the area of the inner disk from the

area of the outer disk:

The next example gives a further illustration of the procedure.

FIGURE 10

out

A 苷

␲

共outer radius兲

⫺

␲

共inner radius兲

out

A 苷

␲

共radius兲

A共y兲A共x兲

V 苷

A共x兲 dx or V 苷

A共y兲 dy

苷

␲

苷

␲

冋

⫺ 5

⫹ 4

册

苷

␲

共x

⫺ 5x

⫹ 4x兲 dx

苷

␲

关共2 ⫺ x

兲

⫺ 共2 ⫺ x兲

兴 dx

V 苷

A共x兲 dx

A共x兲苷

␲

共2 ⫺ x

兲

⫺

␲

共2 ⫺ x兲

SECTION 6.2 VOLUMES

||||

359

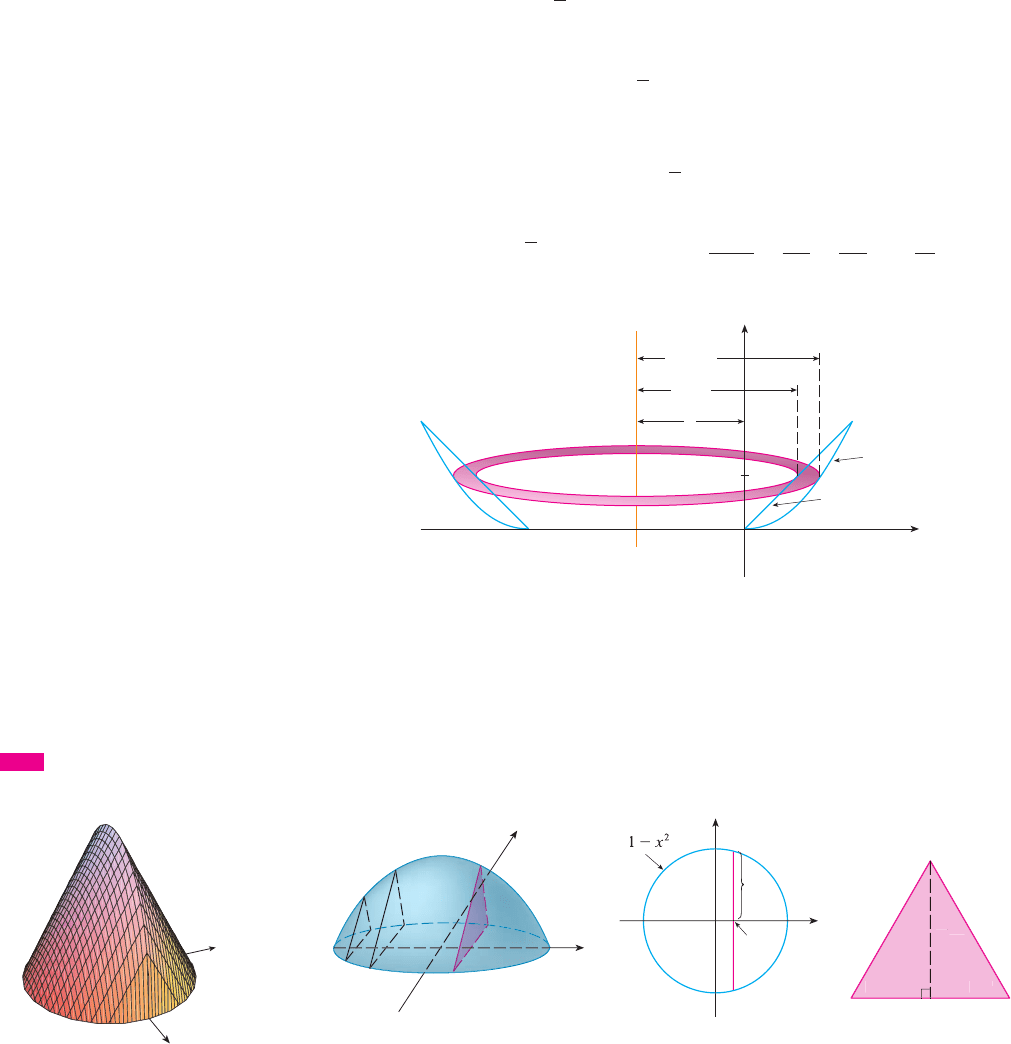
EXAMPLE 6 Find the volume of the solid obtained by rotating the region in Example 4

about the line .

SOLUTION Figure 11 shows a horizontal cross-section. It is a washer with inner radius

and outer radius , so the cross-sectional area is

The volume is

We now ﬁnd the volumes of three solids that are not solids of revolution.

EXAMPLE 7 Figure 12 shows a solid with a circular base of radius 1. Parallel cross-

sections perpendicular to the base are equilateral triangles. Find the volume of the solid.

SOLUTION Let’s take the circle to be . The solid, its base, and a typical cross-

section at a distance from the origin are shown in Figure 13.

URE 1

„

(

)

A cross-sectio

(x,

)

œ„„„„„

„

≈

(

b) Its bas

(

)

The soli

RE 1

Computer-

enerated pictur

of the solid in Exam

⫹ y

苷 1

FIGURE 11

x=_1

x=œ„y

x=y

1+y

1+œ„

苷

␲

冋

3兾2

⫺

册

苷

␲

苷

␲

(

⫺ y ⫺ y

)

苷

␲

[

(

1 ⫹

)

⫺ 共1 ⫹ y兲

]

dy V 苷

A共y兲 dy

苷

␲

(

1 ⫹

)

⫺

␲

共1 ⫹ y兲

A共y兲苷

␲

共outer radius兲

⫺

␲

共inner radius兲

1 ⫹

1 ⫹ y

x 苷 ⫺1

360

||||

CHAPTER 6 APPLICATIONS OF INTEGRATION

Visual 6.2C shows how the solid

in Figure 12 is generated.

TEC

Since lies on the circle, we have and so the base of the triangle

is . Since the triangle is equilateral, we see from Figure 13(c) that its

height is . The cross-sectional area is therefore

and the volume of the solid is

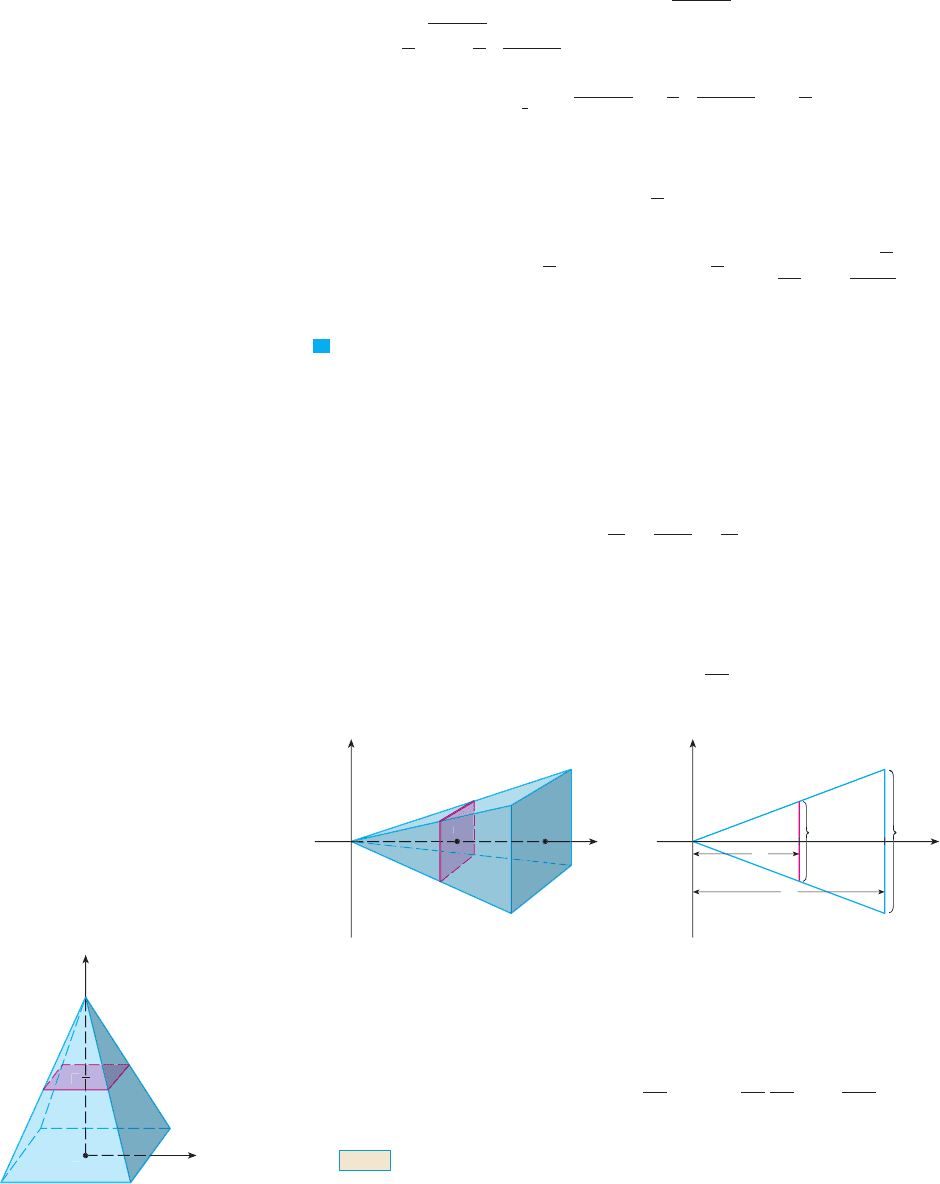
EXAMPLE 8 Find the volume of a pyramid whose base is a square with side and

whose height is .

SOLUTION We place the origin at the vertex of the pyramid and the -axis along its cen-

tral axis as in Figure 14. Any plane that passes through and is perpendicular to the

-axis intersects the pyramid in a square with side of length , say. We can express in

terms of by observing from the similar triangles in Figure 15 that

and so . [Another method is to observe that the line has slope and

so its equation is .] Thus the cross-sectional area is

The pyramid lies between and , so its volume is

We didn’t need to place the vertex of the pyramid at the origin in Example 8.

We did so merely to make the equations simple. If, instead, we had placed the center of the

base at the origin and the vertex on the positive -axis, as in Figure 16, you can verify that y

NOTE

苷

册

苷

V 苷

A共x兲 dx 苷

x 苷 hx 苷 0

URE 1

RE 1

A共x兲苷 s

苷

y 苷 Lx兾共2h兲

L兾共2h兲OPs 苷 Lx兾h

苷

s兾2

L兾2

苷

ssx

苷 2

共1 ⫺ x

兲 dx 苷 2

冋

x ⫺

册

苷

V 苷

⫺1

A共x兲 dx 苷

⫺1

共1 ⫺ x

兲 dx

A共x兲苷

ⴢ 2

1 ⫺ x

ⴢ

1 ⫺ x

苷

共1 ⫺ x

兲

y 苷

1 ⫺ x

ⱍ

苷 2

1 ⫺ x

ABCy 苷

1 ⫺ x

SECTION 6.2 VOLUMES

||||

361

URE 1