Stewart J. Calculus

Подождите немного. Документ загружается.

382

11. A clepsydra, or water clock, is a glass container with a small hole in the bottom through

which water can ﬂow. The “clock” is calibrated for measuring time by placing markings on

the container corresponding to water levels at equally spaced times. Let be continu-

ous on the interval and assume that the container is formed by rotating the graph of

about the -axis. Let denote the volume of water and the height of the water level at time .

(a) Determine as a function of .

(b) Show that

Torricelli’s Law that the rate of change of the volume of the water is given by

where is a negative constant. Determine a formula for the function such that is a

constant . What is the advantage in having ?

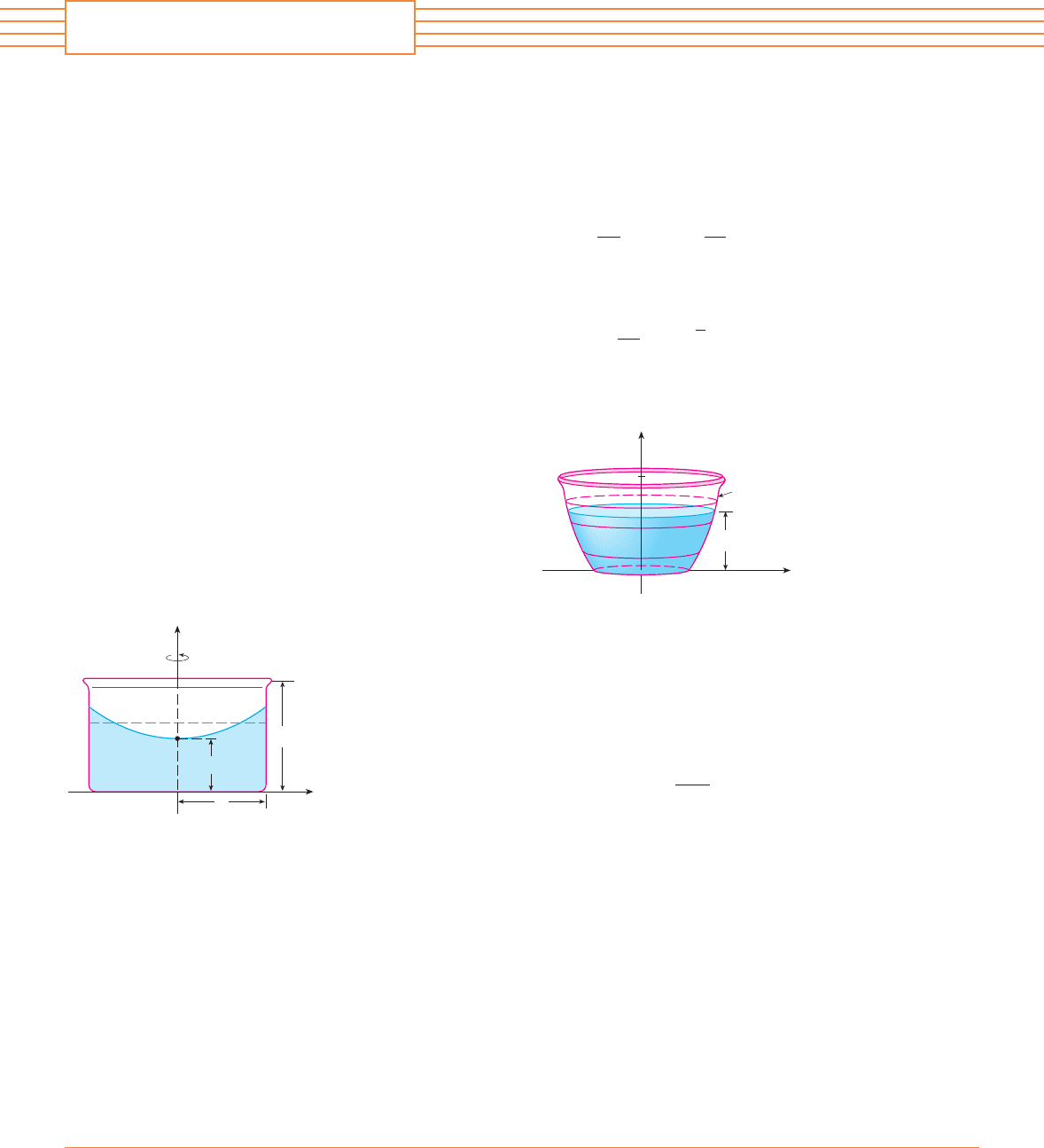
12. A cylindrical container of radius and height is partially ﬁlled with a liquid whose volume

is . If the container is rotated about its axis of symmetry with constant angular speed , then

the container will induce a rotational motion in the liquid around the same axis. Eventually,

the liquid will be rotating at the same angular speed as the container. The surface of the liquid

will be convex, as indicated in the ﬁgure, because the centrifugal force on the liquid particles

increases with the distance from the axis of the container. It can be shown that the surface of

the liquid is a paraboloid of revolution generated by rotating the parabola

about the -axis, where is the acceleration due to gravity.

(a) Determine as a function of .

(b) At what angular speed will the surface of the liquid touch the bottom? At what speed will

it spill over the top?

are rotating at the same constant angular speed. At the central axis the surface of the liquid

is 5 ft below the top of the tank, and 1 ft out from the central axis the surface is 4 ft below

the top of the tank.

(i) Determine the angular speed of the container and the volume of the ﬂuid.

(ii) How far below the top of the tank is the liquid at the wall of the container?

13. Suppose the graph of a cubic polynomial intersects the parabola when , ,

and , where . If the two regions between the curves have the same area, how

is related to ?ab



bx 苷 b

x 苷 ax 苷 0y 苷 x



y 苷 h 



x=f(y)

dh兾dt 苷 CC

dh兾dtfk

苷 kA

苷



关 f 共h兲兴

thVy

f关0, b兴

x 苷 f 共y兲

PROBLEMS PLUS

FIGURE FOR PROBLEM 12

383

14. Suppose we are planning to make a taco from a round tortilla with diameter 8 inches by bend-

ing the tortilla so that it is shaped as if it is partially wrapped around a circular cylinder. We

will ﬁll the tortilla to the edge (but no more) with meat, cheese, and other ingredients. Our

problem is to decide how to curve the tortilla in order to maximize the volume of food it can

hold.

(a) We start by placing a circular cylinder of radius along a diameter of the tortilla and

folding the tortilla around the cylinder. Let represent the distance from the center of the

tortilla to a point on the diameter (see the ﬁgure). Show that the cross-sectional area of

the ﬁlled taco in the plane through perpendicular to the axis of the cylinder is

and write an expression for the volume of the ﬁlled taco.

(b) Determine (approximately) the value of that maximizes the volume of the taco. (Use a

graphical approach with your CAS.)

15. If the tangent at a point on the curve intersects the curve again at , let be the

area of the region bounded by the curve and the line segment . Let be the area of the

region deﬁned in the same way starting with instead of . What is the relationship between

and ?BA

BPQ

AQy 苷 x

A共x兲苷 r

16  x



sin

冉

16  x

冊

CAS

PROBLEMS PLUS

384

The common theme that links the functions of this chapter is that they occur as pairs of

inverse functions. In particular, two of the most important functions that occur in

mathematics and its applications are the exponential function and its inverse

function, the logarithmic function . In this chapter we investigate their

properties, compute their derivatives, and use them to describe exponential growth and

decay in biology, physics, chemistry, and other sciences. We also study the inverses of

trigonometric and hyperbolic functions. Finally, we look at a method (l’Hospital’s Rule)

for computing difﬁcult limits and apply it to sketching curves.

There are two possible ways of deﬁning the exponential and logarithmic functions

and developing their properties and derivatives. One is to start with the exponential

function (deﬁned as in algebra or precalculus courses) and then deﬁne the logarithm as

its inverse. That is the approach taken in Sections 7.2, 7.3, and 7.4 and is probably the

most intuitive method. The other way is to start by deﬁning the logarithm as an integral

and then deﬁne the exponential function as its inverse. This approach is followed in

Sections 7.2*, 7.3*, and 7.4* and, although it is less intuitive, many instructors prefer it

because it is more rigorous and the properties follow more easily. You need only read

one of these two approaches (whichever your instructor recommends).

t!x" ! log

f !x" ! a

The exponential and

logarithmic functions are

inverse functions of each other.

INVERSE FUNCTIONS:

EXPONENTIAL,

LOGARITHMIC, AND

INVERSE TRIGONOMETRIC

FUNCTIONS

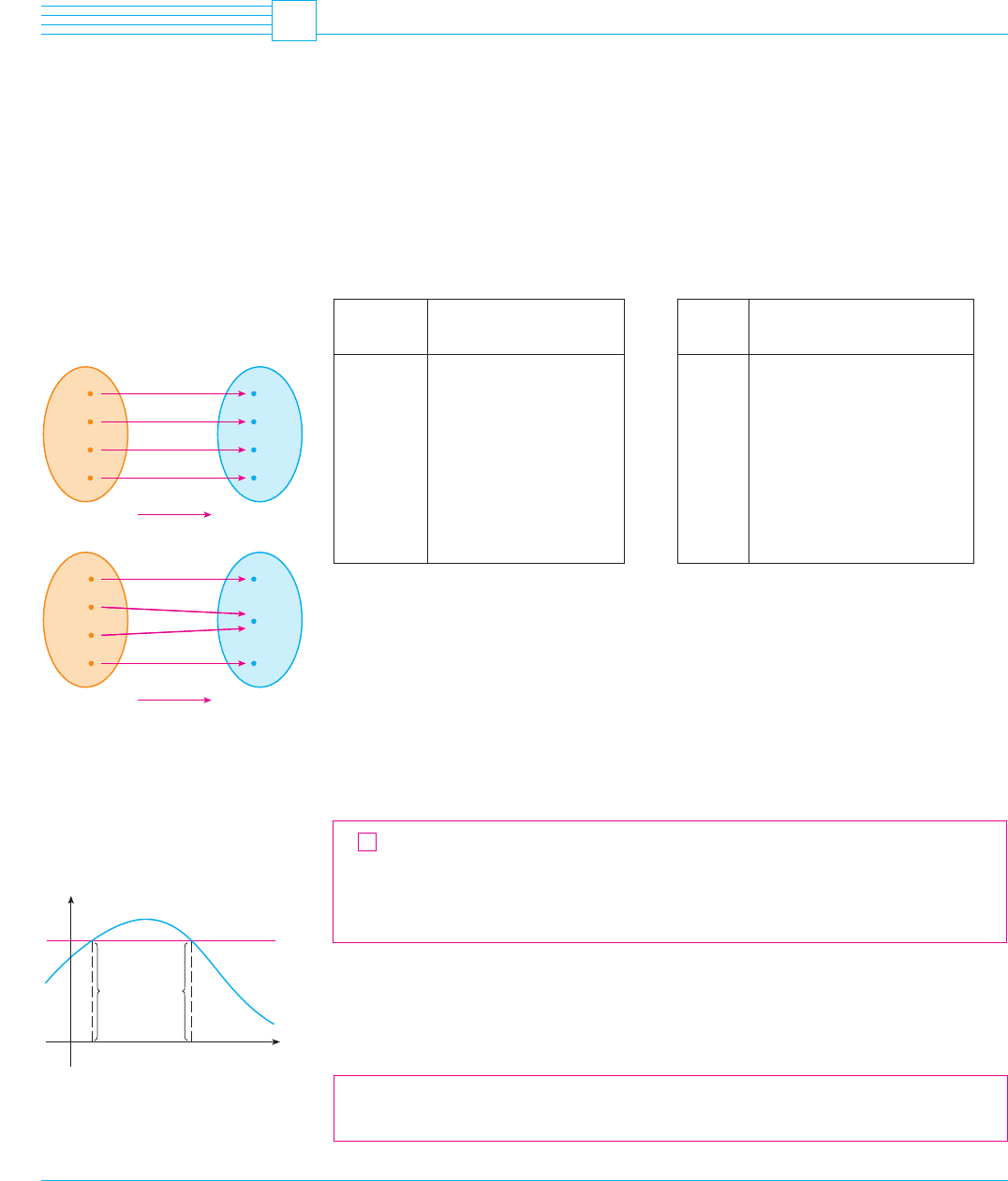
INVERSE FUNCTIONS

Table 1 gives data from an experiment in which a bacteria culture started with 100 bacte-

ria in a limited nutrient medium; the size of the bacteria population was recorded at hourly

intervals. The number of bacteria N is a function of the time t: .

Suppose, however, that the biologist changes her point of view and becomes interested

in the time required for the population to reach various levels. In other words, she is think-

ing of t as a function of N. This function is called the inverse function of f, denoted by ,

and read “f inverse.” Thus is the time required for the population level to reach

N. The values of can be found by reading Table 1 from right to left or by consulting

Table 2. For instance, because

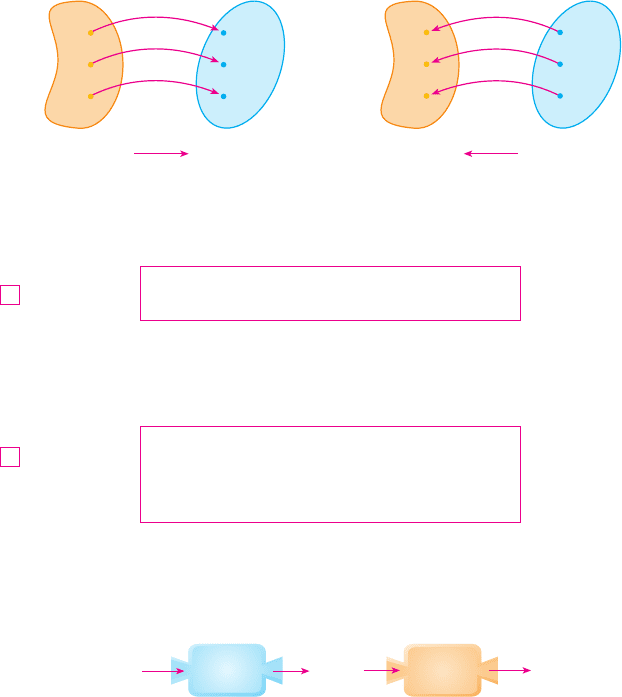
Not all functions possess inverses. Let’s compare the functions and whose arrow

diagrams are shown in Figure 1. Note that never takes on the same value twice (any two

inputs in have different outputs), whereas does take on the same value twice (both 2

and 3 have the same output, 4). In symbols,

but

Functions that share this property with are called one-to-one functions.

DEFINITION A function is called a one-to-one function if it never takes on

the same value twice; that is,

If a horizontal line intersects the graph of in more than one point, then we see from

Figure 2 that there are numbers and such that . This means that is not

one-to-one. Therefore we have the following geometric method for determining whether a

function is one-to-one.

HORIZONTAL LINE TEST A function is one-to-one if and only if no horizontal line

intersects its graph more than once.

ff !x

" ! f !x

whenever x

" x

f !x

" " f !x

whenever x

" x

f !x

" " f !x

t!2" ! t!3"

f !6" ! 550.f

!550" ! 6

t ! f

!N"

N ! f !t"

7.1

385

TA B L E 2 t as a function of N

N ! time to reach N bacteria

100 0

168 1

259 2

358 3

445 4

509 5

550 6

573 7

586 8

t ! f

!N"

TA B L E 1 N as a function of t

(hours) ! population at time t

0 100

1 168

2 259

3 358

4 445

5 509

6 550

7 573

8 586

N ! f !t"

A B

F I G U R E 1

A B

f is one-to-one; g is not

‡ﬂ

y=ƒ

F I G U R E 2

This function is not one-to-one

because f(⁄)=f(¤).

⁄

N In the language of inputs and outputs, this

deﬁnition says that is one-to-one if each out-

put corresponds to only one input.

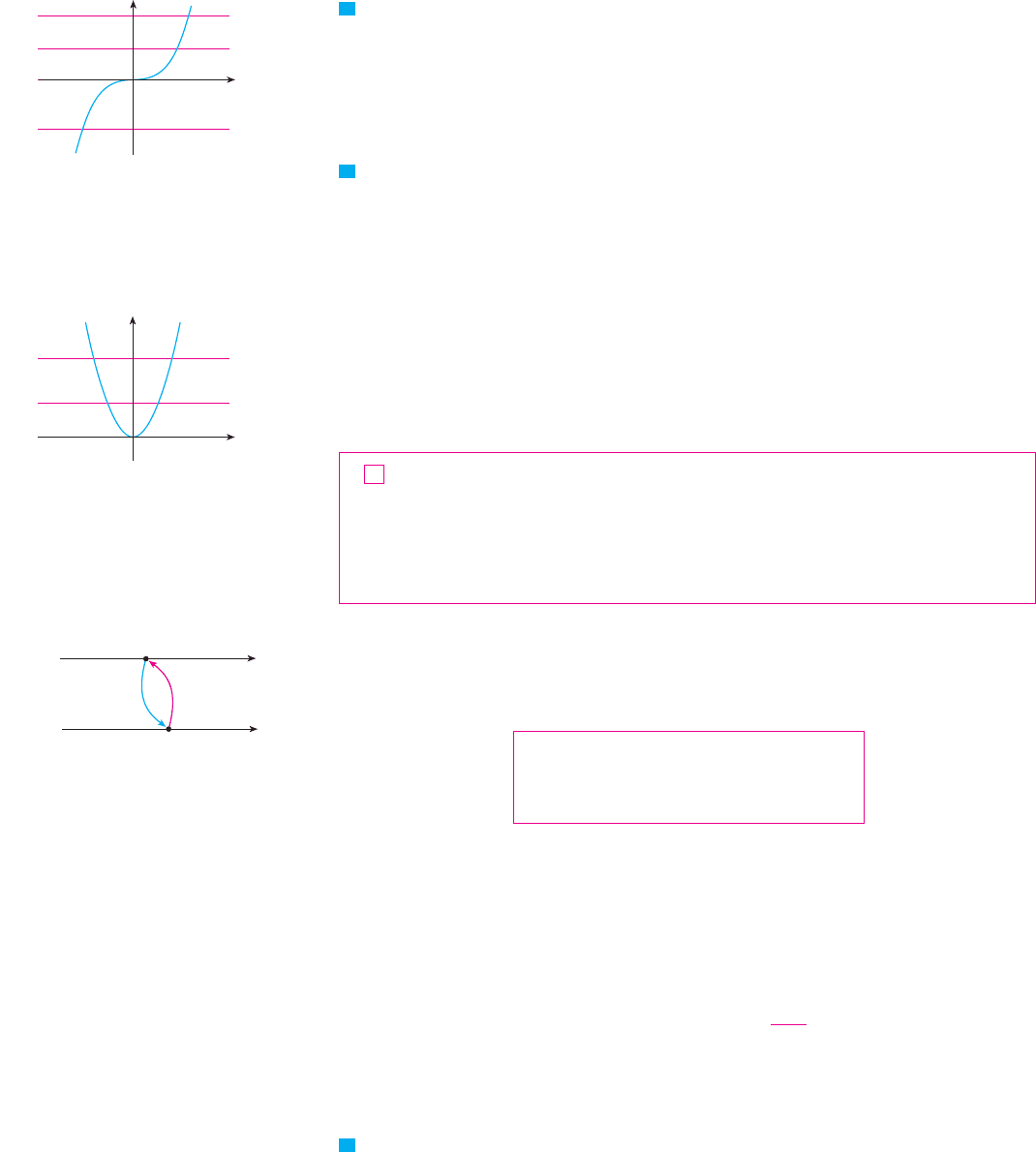
EXAMPLE 1 Is the function one-to-one?

SOLUTION 1 If , then (two different numbers can’t have the same cube).

Therefore, by Deﬁnition 1, is one-to-one.

SOLUTION 2 From Figure 3 we see that no horizontal line intersects the graph of

more than once. Therefore, by the Horizontal Line Test, is one-to-one. M

EXAMPLE 2 Is the function one-to-one?

SOLUTION 1 This function is not one-to-one because, for instance,

and so 1 and have the same output.

SOLUTION 2 From Figure 4 we see that there are horizontal lines that intersect the graph of

more than once. Therefore, by the Horizontal Line Test, is not one-to-one. M

One-to-one functions are important because they are precisely the functions that pos-

sess inverse functions according to the following deﬁnition.

DEFINITION Let be a one-to-one function with domain and range . Then

its inverse function has domain and range and is deﬁned by

for any in .

This deﬁnition says that if maps into , then maps back into . (If were not

one-to-one, then would not be uniquely deﬁned.) The arrow diagram in Figure 5 indi-

cates that reverses the effect of . Note that

For example, the inverse function of is because if , then

CAUTION

Do not mistake the in for an exponent. Thus

The reciprocal could, however, be written as .

EXAMPLE 3 If , , and , ﬁnd

and .f

!!10"

!5",f

!7",f !8" ! !10f !3" ! 7f !1" ! 5

# f !x"$

1%f !x"

f !x"

does not meanf

!x"

!y" ! f

" ! !x

1%3

! x

y ! x

!x" ! x

1%3

f !x" ! x

range of f

! domain of f

domain of f

! range of f

fxyf

yxf

f !x" ! y&?f

!y" ! x

ABf

BAf

t!1" ! 1 ! t!!1"

t!x" ! x

f !x" ! x

" x

f !x" ! x

386

|| ||

CHAPTER 7 INVERSE FUNCTIONS

F I G U R E 3

ƒ=˛ is one-to-one.

y=˛

f –!

F I G U R E 5

F I G U R E 4

=≈ is not one-to-one.

y=≈

SOLUTION

From the deﬁnition of we have

The diagram in Figure 6 makes it clear how reverses the effect of in this case.

The letter is traditionally used as the independent variable, so when we concentrate

on rather than on , we usually reverse the roles of and in Deﬁnition 2 and write

By substituting for in Deﬁnition 2 and substituting for in (3), we get the following

cancellation equations:

The ﬁrst cancellation equation says that if we start with , apply , and then apply we

arrive back at , where we started (see the machine diagram in Figure 7). Thus undoes

what does. The second equation says that undoes what does.

For example, if , then and so the cancellation equations become

These equations simply say that the cube function and the cube root function cancel each

other when applied in succession.

Now let’s see how to compute inverse functions. If we have a function and are

able to solve this equation for in terms of , then according to Deﬁnition 2 we must have

. If we want to call the independent variable x, we then interchange and and

arrive at the equation .y ! f

!x"

yxx ! f

!y"

y ! f !x"

f ! f

!x"" ! !x

1%3

! x

! f !x"" ! !x

1%3

! x

!x" ! x

1%3

f !x" ! x

F I G U R E 7

x x

f –!

,fx

f ! f

!x"" ! x for every x in B

! f !x"" ! x for every x in A

f !y" ! x&?f

!x" ! y

yxff

F I G U R E 6

The inverse function reverses

inputs and outputs.

_10

f –!

_10

f !8" ! !10becausef

!!10" ! 8

f !1" ! 5becausef

!5" ! 1

f !3" ! 7becausef

!7" ! 3

SECTION 7.1 INVERSE FUNCTIONS

|| ||

387

Openmirrors.com

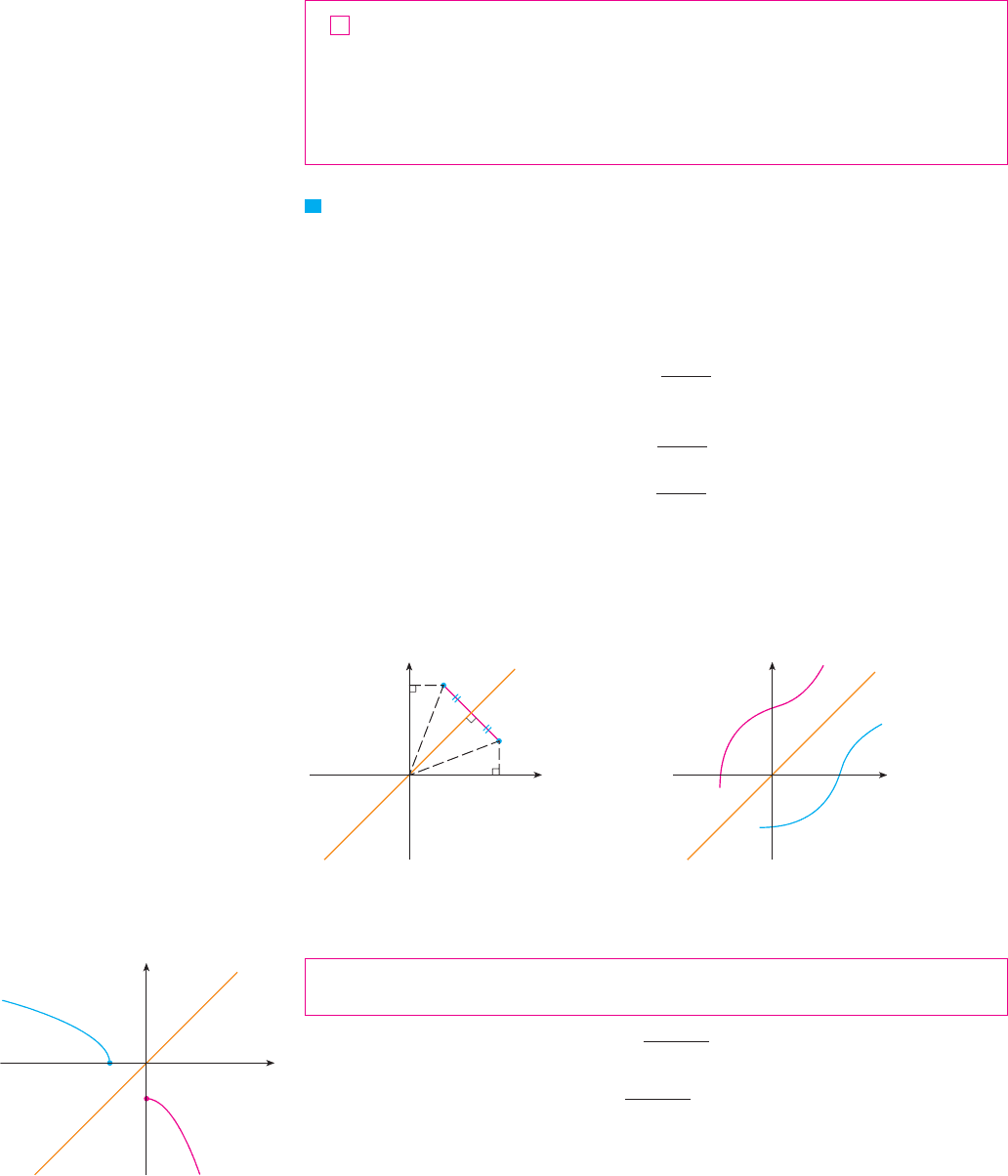
HOW TO FIND THE INVERSE FUNCTION OF A ONE-TO-ONE FUNCTION f

STEP 1 Write .

STEP 2 Solve this equation for in terms of (if possible).

STEP 3 To express as a function of x, interchange and .

The resulting equation is .

EXAMPLE 4 Find the inverse function of .

SOLUTION According to (5) we ﬁrst write

Then we solve this equation for :

Finally, we interchange and :

Therefore the inverse function is . M

The principle of interchanging and to ﬁnd the inverse function also gives us the

method for obtaining the graph of from the graph of . Since if and only if

, the point is on the graph of if and only if the point is on the

graph of . But we get the point from by reﬂecting about the line . (See

Figure 8.)

Therefore, as illustrated by Figure 9:

The graph of is obtained by reﬂecting the graph of about the line .

EXAMPLE 5 Sketch the graphs of and its inverse function using the

same coordinate axes.

SOLUTION First we sketch the curve (the top half of the parabola

, or ) and then we reﬂect about the line to get the

graph of . (See Figure 10.) As a check on our graph, notice that the expression for

is . So the graph of is the right half of the parabola

and this seems reasonable from Figure 10. My ! !x

! 1

!x" ! !x

! 1, x " 0f

y ! xx ! !y

! 1y

! !1 ! x

y !

!1 ! x

f !x" !

!1 ! x

y ! xff

F I G U R E 8

F I G U R E 9

(b,a)

(a,b)

y=x

f –!

y=x

y ! x!a, b"!b, a"f

!b, a"f!a, b"f

!b" ! a

f !a" ! bff

!x" !

x ! 2

y !

x ! 2

x !

y ! 2

! y ! 2

y ! x

# 2

f !x" ! x

# 2

y ! f

!x"

yxf

y ! f !x"

388

|| ||

CHAPTER 7 INVERSE FUNCTIONS

N In Example 4, notice how reverses the

effect of . The function is the rule “Cube,

then add 2”; is the rule “Subtract 2, then

take the cube root.”

y=x

y=ƒ

(0,_1)

y=f –!(x)

(_1,0)

F I G U R E 1 0

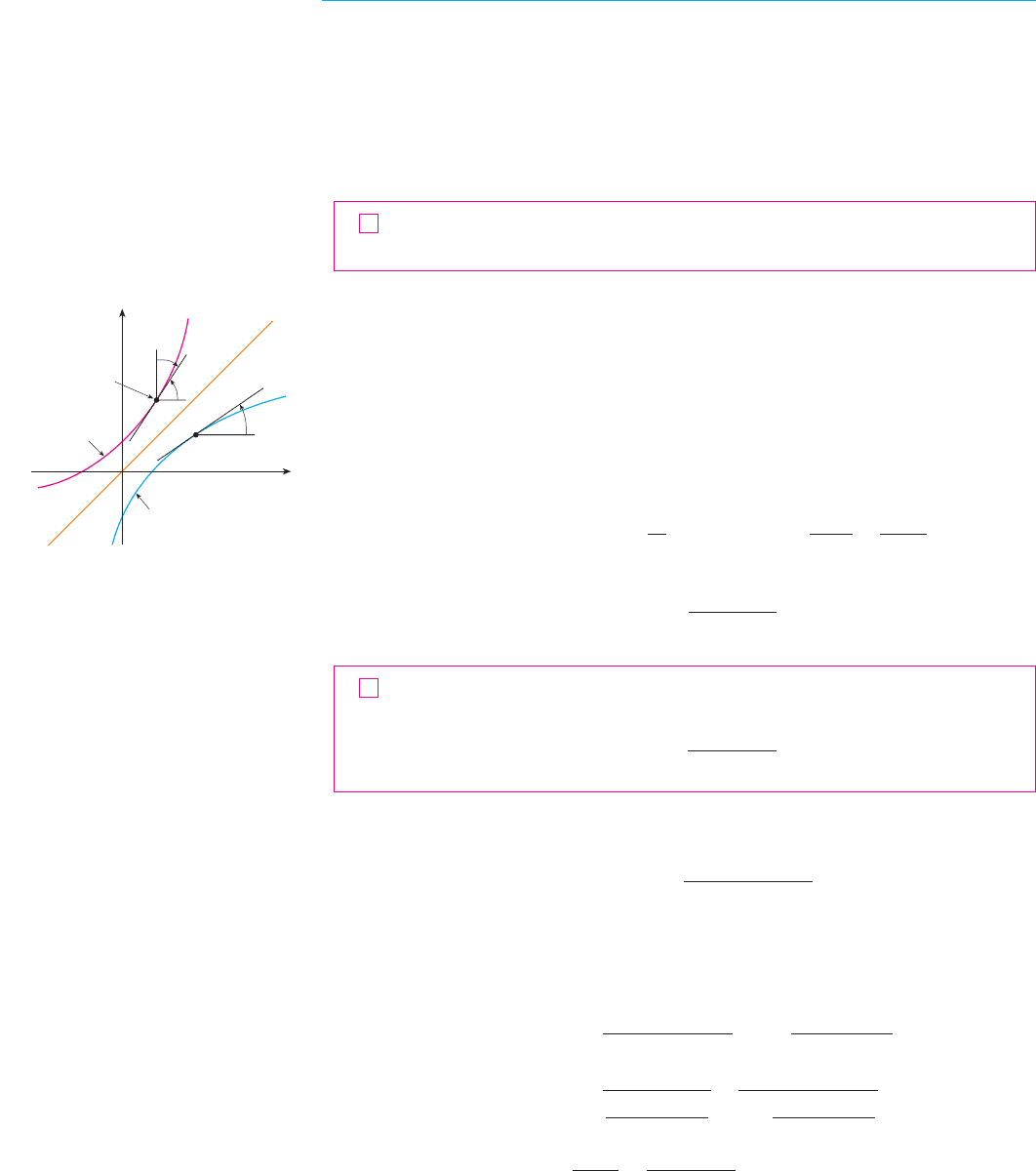
THE CALCULUS OF INVERSE FUNCTIONS

Now let’s look at inverse functions from the point of view of calculus. Suppose that is

both one-to-one and continuous. We think of a continuous function as one whose graph has

no break in it. (It consists of just one piece.) Since the graph of is obtained from the

graph of by reﬂecting about the line , the graph of has no break in it either (see

Figure 9). Thus we might expect that is also a continuous function.

This geometrical argument does not prove the following theorem but at least it makes

the theorem plausible. A proof can be found in Appendix F.

THEOREM If is a one-to-one continuous function deﬁned on an interval, then

its inverse function is also continuous.

Now suppose that is a one-to-one differentiable function. Geometrically we can think

of a differentiable function as one whose graph has no corner or kink in it. We get the graph

of by reﬂecting the graph of about the line , so the graph of has no corner

or kink in it either. We therefore expect that is also differentiable (except where its tan-

gents are vertical). In fact, we can predict the value of the derivative of at a given point

by a geometric argument. In Figure 11 the graphs of and its inverse are shown. If

, then and is the slope of the tangent to the graph of at

, which is . Likewise, . From Figure 11 we see that ,

that is,

THEOREM If is a one-to-one differentiable function with inverse function

and , then the inverse function is differentiable at and

PROOF Write the deﬁnition of derivative as in Equation 3.1.5:

If , then . And if we let , then . Since is differ-

entiable, it is continuous, so is continuous by Theorem 6. Thus if , then

, that is, . Therefore

M !

f $!b"

f $! f

!a""

! lim

f !y" ! f !b"

y ! b

lim

f !y" ! f !b"

y ! b

! f

"$!a" ! lim

!x" ! f

!a"

x ! a

! lim

y ! b

f !y" ! f !b"

y l bf

!x" l f

!a"

x l af

ff !y" ! xy ! f

!x"f

!a" ! bf !b" ! a

! f

"$!a" ! lim

!x" ! f

!a"

x ! a

! f

"$!a" !

f $! f

!a""

af $! f

!a"" " 0

! f

"$!a" !

f $! f

!a""

! f

"$!a" ! tan

! tan

! cot

tan

f $!b"

%2f $!b" ! tan

tan

!a, b"

! f

"$!a"f

!a" ! bf !b" ! a

y ! xff

y ! xf

SECTION 7.1 INVERSE FUNCTIONS

|| ||

389

N Note that because

is one-to-one.

x " a ? f ! y" " f !b"

graph of f

graph

(b,a)

(a, b)

y=x

f –!

F I G U R E 1 1

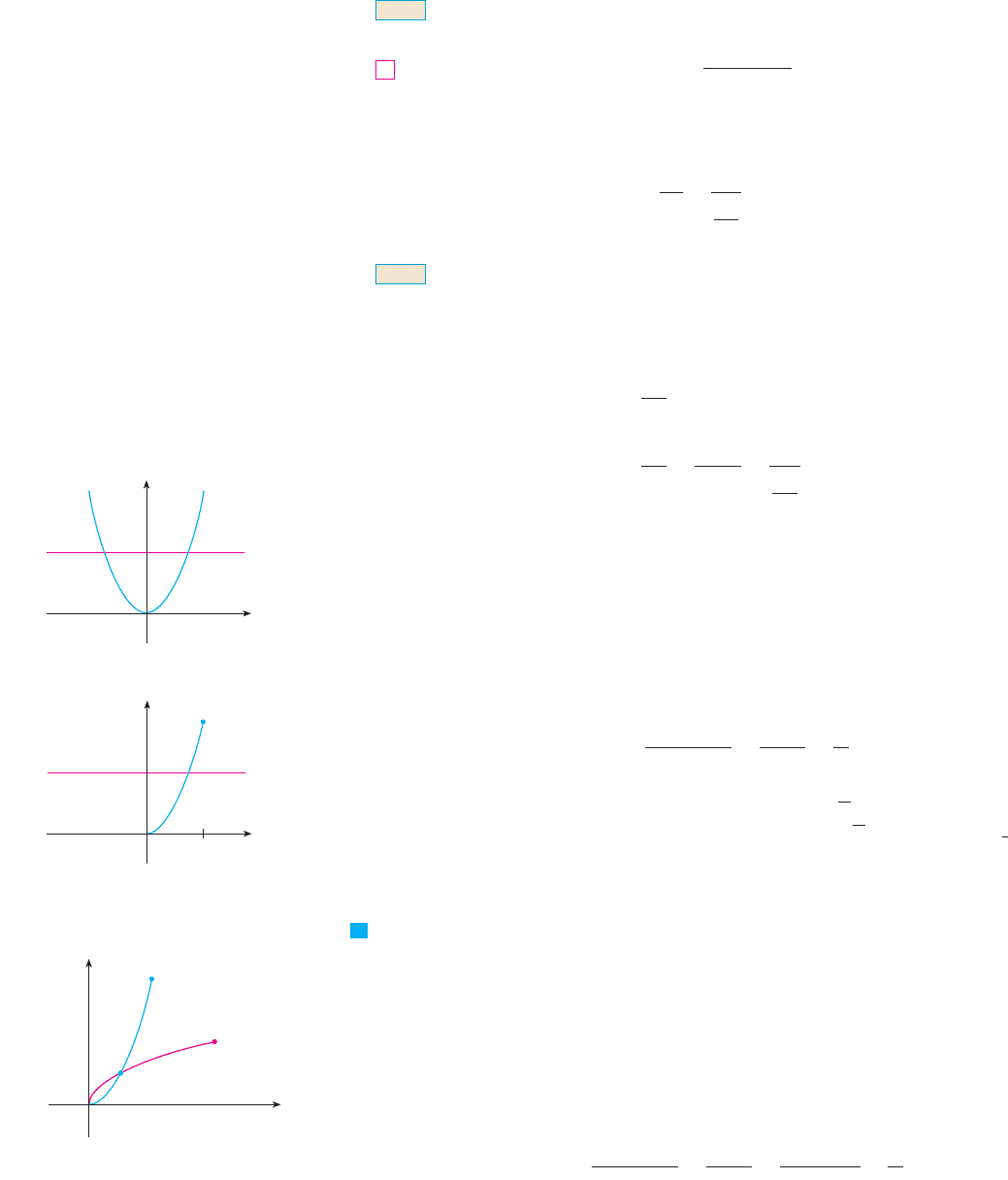
Replacing by the general number in the formula of Theorem 7, we get

If we write , then , so Equation 8, when expressed in Leibniz notation,

becomes

If it is known in advance that is differentiable, then its derivative can be

computed more easily than in the proof of Theorem 7 by using implicit differentiation. If

, then . Differentiating the equation implicitly with respect to

, remembering that is a function of , and using the Chain Rule, we get

Therefore

EXAMPLE 6 Although the function , , is not one-to-one and therefore does

not have an inverse function, we can turn it into a one-to-one function by restricting its

domain. For instance, the function , , is one-to-one (by the Horizon-

tal Line Test) and has domain and range . (See Figure 12.) Thus has an

inverse function with domain and range .

Without computing a formula for we can still calculate . Since

, we have . Also . So by Theorem 7 we have

In this case it is easy to ﬁnd explicitly. In fact, , . [In general,

we could use the method given by (5).] Then , so ,

which agrees with the preceding computation. The functions and are graphed in

Figure 13.

EXAMPLE 7 If , ﬁnd .

SOLUTION Notice that is one-to-one because

and so is increasing. To use Theorem 7 we need to know and we can ﬁnd it by

inspection:

Therefore M

! f

"$!1" !

f $! f

!1""

f $!0"

2 ! sin 0

!1" ! 0?f !0" ! 1

!1"f

f $!x" ! 2 ! sin x ( 0

! f

"$!1"f !x" ! 2x # cos x

! f

!1" !

! f

!x" ! 1%

(

)

0 ) x ) 4f

!x" !

! f

!1" !

f $! f

!1""

f $!1"

f $!x" ! 2xf

!1" ! 1f !1" ! 1

! f

!1"! f

#0, 2$#0, 4$f

f#0, 4$#0, 2$

0 ) x ) 2f !x" ! x

x ! !y ! x

f $!y"

! 1

xyx

f !y" ! xf !y" ! xy ! f

!x"

NOTE 2

f !y" ! xy ! f

!x"

! f

"$!x" !

f $! f

!x""

NOTE 1

390

|| ||

CHAPTER 7 INVERSE FUNCTIONS

F I G U R E 1 2

(a) y=≈, x ! R

(2,4)

(b) ƒ=≈, 0¯x¯2

(2,4)

(4,2)

(1,1)

F I G U R E 1 3

f –!

SECTION 7.1 INVERSE FUNCTIONS

|| ||

391

(d) Estimate the value of .

The formula , where , expresses

the Celsius temperature C as a function of the Fahrenheit tem-

perature F. Find a formula for the inverse function and interpret

it. What is the domain of the inverse function?

22. In the theory of relativity, the mass of a particle with speed is

where is the rest mass of the particle and is the speed of

light in a vacuum. Find the inverse function of and explain

its meaning.

23–28 Find a formula for the inverse of the function.

23.

25. 26.

27. 28.

;

29–30 Find an explicit formula for and use it to graph ,

and the line on the same screen. To check your work, see

whether the graphs of and are reﬂections about this line.

29. , 30. ,

31–32 Use the given graph of to sketch the graph of .

31. 32.

33 –36

(a) Show that is one-to-one.

(b) Use Theorem 7 to ﬁnd .

!x"

! f

"$!a"

x ( 0

f !x" !

# 2x

x " 0f !x" ! x

# 1

y ! x

x " 2f !x " ! 2 x

! 8 xy !

1 !

1 #

y ! 2x

# 3f !x" !

10 ! 3x

f !x" !

4x ! 1

2x # 3

24.

f!x " ! 3 ! 2x

m ! f !v" !

1 ! v

F " !459.67C !

!F ! 32"

21.

!0"

!2"

1. (a) What is a one-to-one function?

(b) How can you tell from the graph of a function whether it is

one-to-one?

2. (a) Suppose is a one-to-one function with domain and

range . How is the inverse function deﬁned? What is

the domain of ? What is the range of ?

(b) If you are given a formula for , how do you ﬁnd a

formula for ?

of ?

3–16 A function is given by a table of values, a graph, a formula, or

a verbal description. Determine whether it is one-to-one.

5. 6.

9. 10.

11. 12.

13.

14.

is the height of a football t seconds after kickoff.

16. is your height at age t.

17. If is a one-to-one function such that , what

is ?

18. If , ﬁnd .

If , ﬁnd .

20. The graph of is given.

(a) Why is one-to-one?

(b) What are the domain and range of ?f

!6"h!x" ! x #

19.

!1"f !x" ! x # cos x

!9"

f !2" ! 9f

f !t"

15.

0 ) x )

h!x" ! 1 # cos x

t!x" !

(

t!x" ! 1%x

f !x" ! 10 ! 3xf !x" ! x

! 2x

E X E R C I S E S

7.1

x 1 2 3 4 5 6

1.5 2.0 3.6 5.3 2.8 2.0f !x"

x 1 2 3 4 5 6

1 2 4 8 16 32f !x"