Stewart J. Calculus

Подождите немного. Документ загружается.

402

|| ||

CHAPTER 7 INVERSE FUNCTIONS

17–18 Find the exponential function whose graph is

given.

18.

19. Suppose the graphs of and are drawn on

a coordinate grid where the unit of measurement is 1 inch.

Show that, at a distance 2 ft to the right of the origin, the

height of the graph of is 48 ft but the height of the graph

of is about 265 mi.

;

20. Compare the rates of growth of the functions and

by graphing both functions in several viewing rect-

angles. Find all points of intersection of the graphs correct to

one decimal place.

;

Compare the functions and by graphing

both and in several viewing rectangles. When does the

graph of ﬁnally surpass the graph of ?

;

22. Use a graph to estimate the values of such that

23–30 Find the limit.

23. 24.

25. 26.

27. 28.

29. 30.

lim

)

#2"

tan x

lim

!2x

cos x"

lim

3#!2!x"

lim

3#!2!x"

lim

x l %

! e

!3x

" e

!3x

lim

!1.001"

lim

x l %

!1.001"

# 1,000,000,000

t!x" ! e

f !x" ! x

21.

t!x" ! 5

f !x" ! x

t!x" ! 2

f !x" ! x

”2, ’

(1,6)

(3,24)

17.

f !x" ! Ca

1. (a) Write an equation that deﬁnes the exponential function

with base .

(b) What is the domain of this function?

(d) Sketch the general shape of the graph of the exponential

function for each of the following cases.

(i) (ii) (iii)

2. (a) How is the number deﬁned?

(b) What is an approximate value for ?

;

3–6 Graph the given functions on a common screen. How are

these graphs related?

3. , , ,

4. , , ,

, , ,

6. , , ,

7–12 Make a rough sketch of the graph of the function. Do not

use a calculator. Just use the graphs given in Figures 3 and 12 and,

if necessary, the transformations of Section 1.3.

7. 8.

10.

12.

Starting with the graph of , write the equation of the

graph that results from

(a) shifting 2 units downward

(b) shifting 2 units to the right

(d) reﬂecting about the y-axis

(e) reﬂecting about the x-axis and then about the y-axis

14. Starting with the graph of , ﬁnd the equation of the

graph that results from

(a) reﬂecting about the line

(b) reﬂecting about the line

15–16 Find the domain of each function.

15. (a) (b)

16. (a) (b)

t!t" !

1 ! 2

t!t" ! sin!e

f !x" !

1 ! e

f !x" !

1 " e

x ! 2

y ! 4

y ! e

13.

y ! 2!1 ! e

"y ! 1 !

11.

y ! 1 " 2e

y ! !2

y ! 4

x! 3

y ! 4

! 3

y ! 0.1

y ! 0.3

y ! 0.6

y ! 0.9

y !

(

)

y !

(

)

y ! 10

y ! 3

y ! 8

y ! e

y ! 20

y ! 5

y ! e

y ! 2

a ! 1a # 1

a " 1

a # 0

E X E R CI SE S

7.2

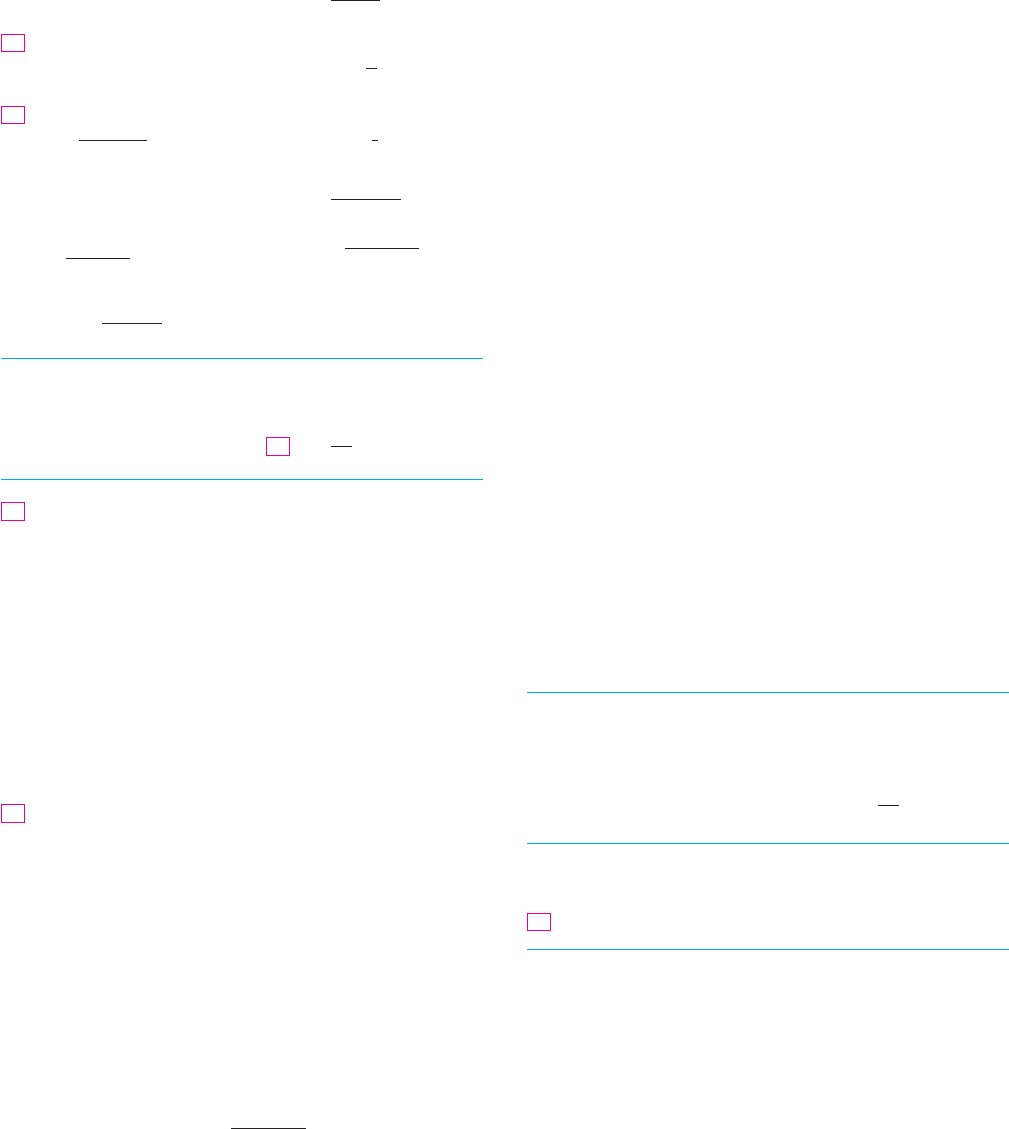
rumor at time and and are positive constants. [In Sec-

tion 10.4 we will see that this is a reasonable model for .]

(a) Find .

(b) Find the rate of spread of the rumor.

;

hours. Use the graph to estimate how long it will take for

80% of the population to hear the rumor.

;

60. An object is attached to the end of a vibrating spring

and its displacement from its equilibrium position is

, where is measured in seconds and is

measured in centimeters.

(a) Graph the displacement function together with the func-

tions and . How are these graphs

related? Can you explain why?

(b) Use the graph to estimate the maximum value of the dis-

placement. Does it occur when the graph touches the

graph of ?

its equilibrium position?

(d) Use the graph to estimate the time after which the

displacement is no more than 2 cm from equilibrium.

61. Find the absolute maximum value of the function

62. Find the absolute minimum value of the function

, .

63–64 Find the absolute maximum and absolute minimum values

of on the given interval.

63. , 64. ,

65–66 Find (a) the intervals of increase or decrease, (b) the inter-

vals of concavity, and (c) the points of inﬂection.

65. 66.

67–68 Discuss the curve using the guidelines of Section 4.5.

68.

;

69. A drug response curve describes the level of medication in

the bloodstream after a drug is administered. A surge

function is often used to model the response

curve, reﬂecting an initial surge in the drug level and then a

more gradual decline. If, for a particular drug,

, and is measured in minutes, estimate the

times corresponding to the inﬂection points and explain their

signiﬁcance. If you have a graphing device, use it to graph

the drug response curve.

tp ! 4, k ! 0.07

A ! 0.01,

S!t" ! At

!kt

y ! e

sin xy ! e

!1#!x"1"

67.

f !x" !

f !x" ! !1 ! x"e

)!1, 6*f !x" ! x

!x#2

)!1, 4*f !x" ! xe

x # 0t!x" ! e

f !x" ! x ! e

y ! 8e

!t#2

y ! !8e

!t#2

y ! 8e

!t#2

yty ! 8e

!t#2

sin 4t

tk ! 0.5a ! 10p

lim

t l %

p!t"

kat

31– 46 Differentiate the function.

31. 32.

34.

35. 36.

38.

39. 40.

41. 42.

43. 44.

45. 46.

47– 48 Find an equation of the tangent line to the curve at the

given point.

47. ,

Find if .

50. Find an equation of the tangent line to the curve

at the point .

51. Show that the function satisﬁes the differen-

tial equation .

52. Show that the function satisﬁes the differ-

ential equation .

53. For what values of does the function satisfy the

equation ?

54. Find the values of for which satisﬁes the equation

If , ﬁnd a formula for .

56. Find the thousandth derivative of .

57. (a) Use the Intermediate Value Theorem to show that there is

a root of the equation .

(b) Use Newton’s method to ﬁnd the root of the equation in

part (a) correct to six decimal places.

;

58. Use a graph to ﬁnd an initial approximation (to one decimal

place) to the root of the equation .

Then use Newton’s method to ﬁnd the root correct to eight

decimal places.

59. Under certain circumstances a rumor spreads according to the

equation

where is the proportion of the population that knows the p!t"

p!t" !

1 " ae

!kt

sin x ! x

! x " 1

" x ! 0

f !x" ! xe

!n"

!x"f !x" ! e

55.

y " y& ! y'

y ! e

y' " 6y& " 8y ! 0

y ! e

y' " 2y& " y ! 0

y ! Ae

" Bxe

2y' ! y& ! y ! 0

y ! e

" e

! x / 2

!0, 1"xe

" ye

! 1

! x " yy&

49.

!1, e"y !

48.

y ! e

cos

)

x, !0, 1"

f !t" ! sin

sin

"y ! cos

1 ! e

1 " e

y !

1 " xe

!2x

y !

" b

" d

y !

! e

" e

y ! e

k tan

y !

1 " 2e

f !t" ! sin!e

" " e

sin t

F!t" ! e

t sin 2t

37.

t!x" !

f !u" ! e

1#u

y ! e

!cos u " cu"y ! e

33.

y !

1 " x

f !x" ! !x

" 2x"e

SECTION 7.2 EXPONENTIAL FUNCTIONS AND THEIR DERIVATIVES

|| ||

403

87. The error function

is used in probability, statistics, and engineering.

(a) Show that .

(b) Show that the function satisﬁes the differ-

ential equation .

88. A bacteria population starts with 400 bacteria and grows at a

rate of bacteria per hour. How many

bacteria will there be after three hours?

89. If , ﬁnd .

90. Evaluate .

;

91. If you graph the function

you’ll see that appears to be an odd function. Prove it.

;

92. Graph several members of the family of functions

where . How does the graph change when changes?

How does it change when changes?

93. (a) Show that if .

[Hint: Show that is increasing

for .]

(b) Deduce that .

94. (a) Use the inequality of Exercise 93(a) to show that, for

(b) Use part (a) to improve the estimate of given in

Exercise 93(b).

95. (a) Use mathematical induction to prove that for and

any positive integer ,

(b) Use part (a) to show that .

for any positive integer .k

lim

x l !

! !

e " 2.7

# 1 $ x $

$ % % % $

x # 0

# 1 $ x $

x # 0,

& x

dx & e

x " 0

f !x" ! e

' !1 $ x"

x # 0e

# 1 $ x

ba " 0

f !x" !

1 $ ae

f !x" !

1 ' e

1#x

1 $ e

1#x

lim

x l

(

sin x

' 1

x '

(

! f

")!4"f !x" ! 3 $ x $ e

r!t" ! !450.268"e

1.12567t

y) ! 2xy $ 2#

(

y ! e

erf!x"

dt !

(

$erf!b" ' erf!a"%

erf!x" !

(

;

70 – 71 Draw a graph of that shows all the important aspects of

the curve. Estimate the local maximum and minimum values and

then use calculus to ﬁnd these values exactly. Use a graph of

to estimate the inﬂection points.

70. 71.

72. The family of bell-shaped curves

occurs in probability and statistics, where it is called the nor-

mal density function. The constant is called the mean and

the positive constant is called the standard deviation. For

simplicity, let’s scale the function so as to remove the factor

and let’s analyze the special case where .

So we study the function

(a) Find the asymptote, maximum value, and inﬂection points

of .

(b) What role does play in the shape of the curve?

;

same screen.

73– 82 Evaluate the integral.

73. 74.

76.

77. 78.

79. 80.

82.

83. Find, correct to three decimal places, the area of the region

bounded by the curves , , and .

84. Find if , , and .

85. Find the volume of the solid obtained by rotating about the

-axis the region bounded by the curves , , ,

and .

Find the volume of the solid obtained by rotating about the

-axis the region bounded by the curves , ,

, and .x ! 1x ! 0

y ! 0y ! e

86.

x ! 1

x ! 0y ! 0y ! e

f )!0" ! 2f !0" ! 1f *!x" ! 3e

$ 5 sin xf !x"

x ! 1y ! e

y ! e

sin!e

" dx

81.

1#x

sin x e

cos x

!4 $ e

$ e

!1 $ e

1 $ e

75.

'3x

f !x" ! e

#!2

! 01#

(

)

y !

(

'!x'

#!2

f !x" ! e

cos x

f *

404

|| ||

CHAPTER 7 INVERSE FUNCTIONS

LOG ARIT HMI C FUN CTI O NS

If and , the exponential function is either increasing or decreasing

and so it is one-to-one. It therefore has an inverse function , which is called the logarith-

mic function with base a and is denoted by . If we use the formulation of an inverse

function given by (7.1.3),

then we have

Thus, if , then is the exponent to which the base must be raised to give .

EXAMPLE 1 Evaluate (a) , (b) , and (c) .

SOLUTION

(a) because

(b) because

The cancellation equations (7.1.4), when applied to and ,

become

The logarithmic function has domain and range and is continuous since it

is the inverse of a continuous function, namely, the exponential function. Its graph is the

reﬂection of the graph of about the line .

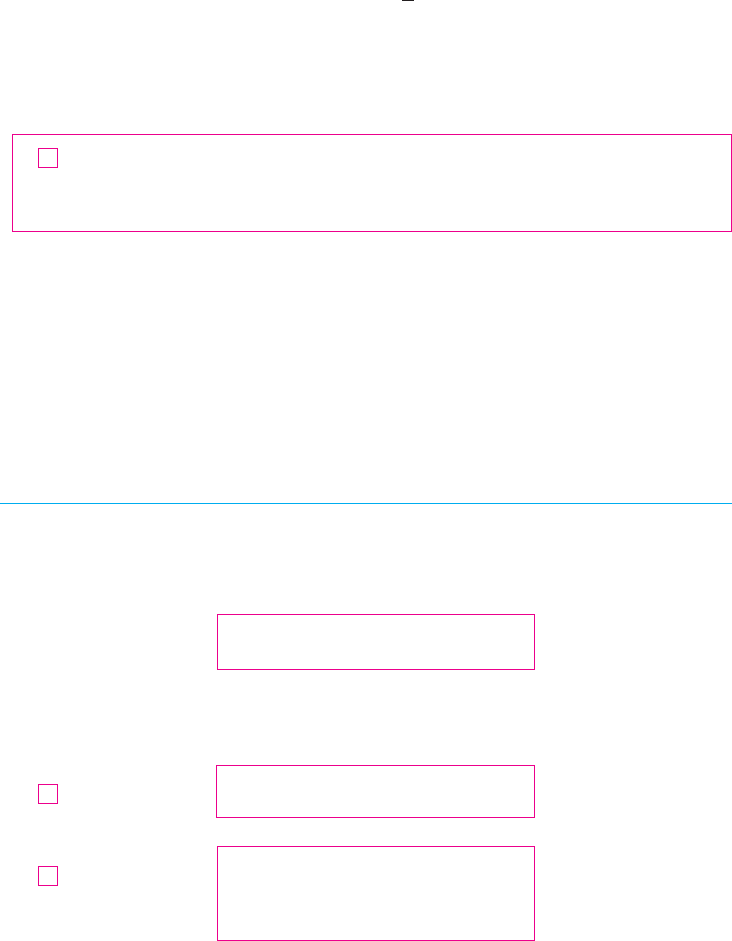
Figure 1 shows the case where . (The most important logarithmic functions have

base .) The fact that is a very rapidly increasing function for is

reﬂected in the fact that is a very slowly increasing function for .

Figure 2 shows the graphs of with various values of the base . Since

, the graphs of all logarithmic functions pass through the point .

The following theorem summarizes the properties of logarithmic functions.

THEOREM If , the function is a one-to-one, continuous,

increasing function with domain and range . If , and r is any real

number, then

3. log

" ! r log

log

! log

x ' log

log

!xy" ! log

x $ log

y " 0x!!0, !"

f !x" ! log

xa " 1

!1, 0"log

1 ! 0

ay ! log

x " 1y ! log

x " 0y ! a

a " 1

y ! xy ! a

!!0, !"log

log

! x for every x " 0

log

" ! x for every x ! !

!x" ! log

xf !x" ! a

! 0.001log

0.001 ! '3

1#2

! 5log

5 !

! 81log

81 ! 4

log

0.001log

5log

xalog

xx " 0

! x&?log

x ! y

f !y" ! x&?f

!x" ! y

log

f !x" ! a

a " 1a " 0

7.3

SECTION 7.3 LOGARITHMIC FUNCTIONS

|| ||

405

y=x

y=a®,a>1

y=log

x, a>1

F I G U R E 1

F I G U R E 2

y=log£x

y=log™x

y=log∞x

y=log¡¸x

Properties 1, 2, and 3 follow from the corresponding properties of exponential functions

given in Section 7.2.

EXAMPLE 2 Use the properties of logarithms in Theorem 3 to evaluate the following.

(a) (b)

SOLUTION

(a) Using Property 1 in Theorem 3, we have

since .

(b) Using Property 2 we have

since .

The limits of exponential functions given in Section 7.2 are reﬂected in the following

limits of logarithmic functions. (Compare with Figure 1.)

If , then

In particular, the -axis is a vertical asymptote of the curve .

EXAMPLE 3 Find .

SOLUTION As , we know that and the values of are positive.

So by (4) with , we have

NATURAL LOGA R I T H M S

Of all possible bases for logarithms, we will see in the next section that the most con-

venient choice of a base is the number , which was deﬁned in Section 7.2. The logarithm

with base is called the natural logarithm and has a special notation:

If we put and replace with “ln” in (1) and (2), then the deﬁning properties

of the natural logarithm function become

ln x

! x x " 0

ln!e

" ! x x ! !

! x&?ln x ! y

log

a ! e

log

x ! ln x

lim

log

!tan

x" ! lim

log

t ! '!

a ! 10 " 1

tt ! tan

x l tan

0 ! 0x l 0

lim

x l 0

log

!tan

y ! log

lim

log

x ! ! and lim

log

x ! '!

a " 1

! 16

log

80 ' log

5 ! log

(

)

! log

16 ! 4

! 64

log

2 $ log

32 ! log

!2 " 32" ! log

64 ! 3

log

80 ' log

5log

2 $ log

406

|| ||

CHAPTER 7 INVERSE FUNCTIONS

N NOTATION FOR LOGARITHMS

Most textbooks in calculus and the sciences, as

well as calculators, use the notation for the

natural logarithm and for the “common

logarithm,” . In the more advanced mathe-

matical and scientiﬁc literature and in computer

languages, however, the notation usually

denotes the natural logarithm.

log x

log

log x

ln x

In particular, if we set , we get

EXAMPLE 4 Find if .

SOLUTION 1 From (5) we see that

Therefore .

(If you have trouble working with the “ln” notation, just replace it by . Then the

equation becomes ; so, by the deﬁnition of logarithm, .)

SOLUTION 2 Start with the equation

and apply the exponential function to both sides of the equation:

But the second cancellation equation in (6) says that . Therefore . M

EXAMPLE 5 Solve the equation .

SOLUTION We take natural logarithms of both sides of the equation and use (6):

Since the natural logarithm is found on scientiﬁc calculators, we can approximate the

solution: to four decimal places, .

EXAMPLE 6 Express as a single logarithm.

SOLUTION Using Properties 3 and 1 of logarithms, we have

The following formula shows that logarithms with any base can be expressed in terms

of the natural logarithm.

! ln

(

)

! ln a $ ln

ln a $

ln b ! ln a $ ln b

1#2

ln a $

ln b

x ( 0.8991

x !

!5 ' ln 10"

3x ! 5 ' ln 10

5 ' 3x ! ln 10

ln!e

5'3x

" ! ln 10

5'3x

! 10

x ! e

ln x

! x

ln x

! e

ln x ! 5

! xlog

x ! 5

log

x ! e

! xmeansln x ! 5

ln x ! 5x

ln e ! 1

x ! 1

SECTION 7.3 LOGARITHMIC FUNCTIONS

|| ||

407

CHANGE OF BASE FORMULA For any positive number , we have

PROOF Let . Then, from (1), we have . Taking natural logarithms of both

sides of this equation, we get . Therefore

Scientiﬁc calculators have a key for natural logarithms, so Formula 7 enables us to use

a calculator to compute a logarithm with any base (as shown in the following example).

Similarly, Formula 7 allows us to graph any logarithmic function on a graphing calculator

or computer (see Exercises 20–22).

EXAMPLE 7 Evaluate correct to six decimal places.

SOLUTION Formula 7 gives

The graphs of the exponential function and its inverse function, the natural log-

arithm function, are shown in Figure 3. Because the curve crosses the y-axis with

a slope of 1, it follows that the reﬂected curve crosses the x-axis with a slope of 1.

In common with all other logarithmic functions with base greater than 1, the natural

logarithm is a continuous, increasing function deﬁned on and the y-axis is a vertical

asymptote.

If we put in (4), then we have the following limits:

EXAMPLE 8 Sketch the graph of the function .

SOLUTION We start with the graph of as given in Figure 3. Using the transforma-

tions of Section 1.3, we shift it 2 units to the right to get the graph of and

then we shift it 1 unit downward to get the graph of . (See Figure 4.)

Notice that the line is a vertical asymptote since

F I G U R E 4

(3,0)

x=2

y=ln(x-2)

y=lnx

(1,0)

x=2

(3,_1)

y=ln(x-2)-1

lim

$ln!x ' 2" ' 1% ! '!

x ! 2

y ! ln!x ' 2" ' 1

y ! ln!x ' 2"

y ! ln x

y ! ln!x ' 2" ' 1

lim

ln x ! ! lim

ln x ! '!

a ! e

!0, !"

y ! ln x

y ! e

log

5 !

ln 5

ln 8

( 0.773976

log

y !

ln x

ln a

y ln a ! ln x

! xy ! log

log

x !

ln x

ln a

!a " 1"a

408

|| ||

CHAPTER 7 INVERSE FUNCTIONS

y=x

y=´

y=lnx

F I G U R E 3

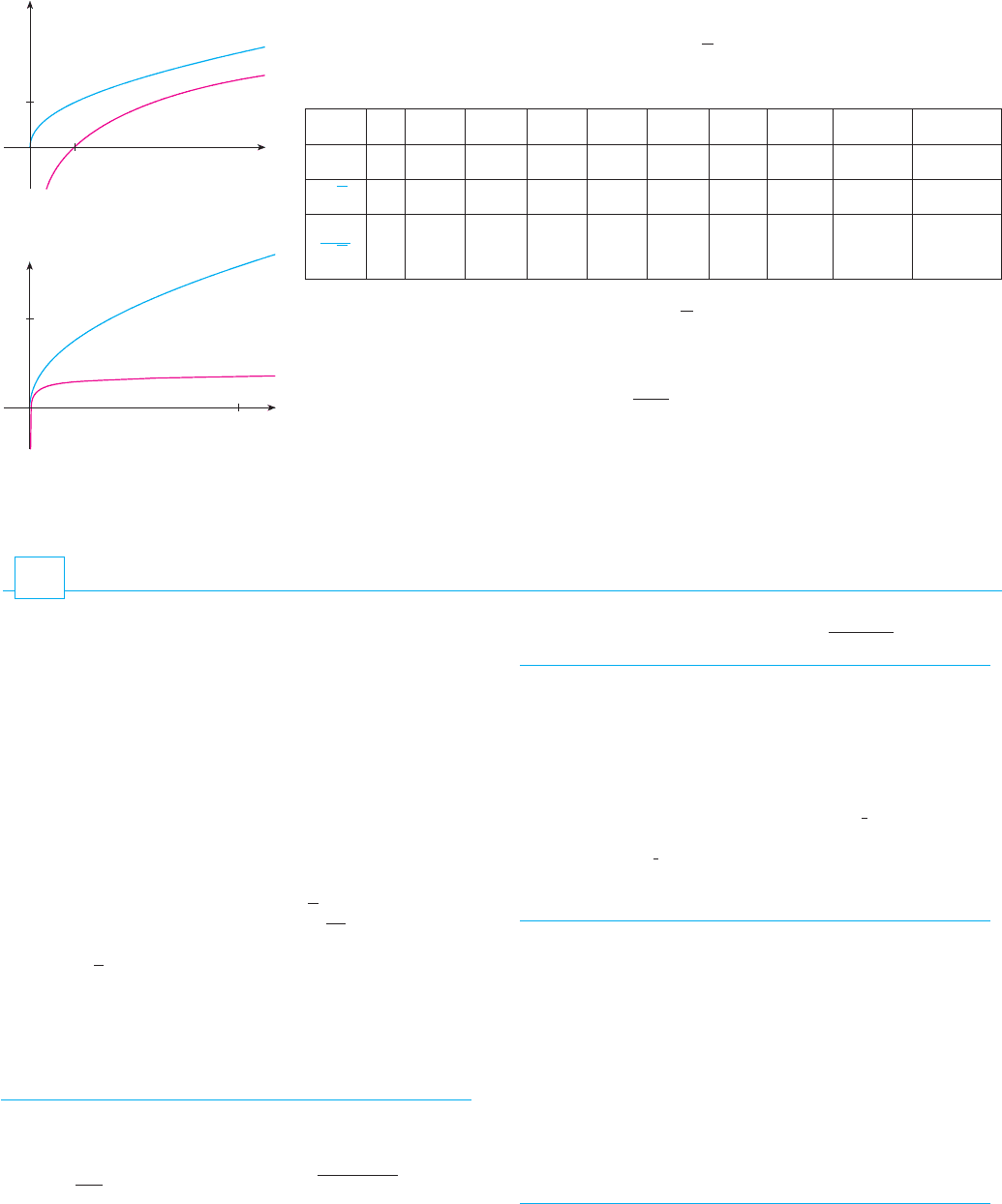
We have seen that as . But this happens very slowly. In fact, grows

more slowly than any positive power of x. To illustrate this fact, we compare approximate

values of the functions and in the following table and we graph

them in Figures 5 and 6.

You can see that initially the graphs of and grow at comparable rates,

but eventually the root function far surpasses the logarithm. In fact, we will be able to show

in Section 7.8 that

for any positive power . So for large , the values of are very small compared with

. (See Exercise 70.)x

ln xxp

lim

x l !

ln x

! 0

y ! ln xy !

y ! x

1#2

y ! ln x

ln xx l !ln x l !

SECTION 7.3 LOGARITHMIC FUNCTIONS

|| ||

409

x 1 2 5 10 50 100 500 1000 10,000 100,000

0 0.69 1.61 2.30 3.91 4.6 6.2 6.9 9.2 11.5

1 1.41 2.24 3.16 7.07 10.0 22.4 31.6 100 316

0 0.49 0.72 0.73 0.55 0.46 0.28 0.22 0.09 0.04

ln x

y=œ

„

y=lnx

F I G U R E 5

1000

y=œ

„

y=lnx

F I G U R E 6

11. 12.

13–18 Express the quantity as a single logarithm.

13.

14.

15. 16.

17.

18.

19. Use Formula 7 to evaluate each logarithm correct to six deci-

mal places.

(a) (b) (c)

;

20 – 22 Use Formula 7 to graph the given functions on a com-

mon screen. How are these graphs related?

20. , , ,

21. , , ,

22. , , , y ! 10

y ! e

y ! log

xy ! ln x

y ! log

xy ! log

xy ! ln xy ! log

1.5

y ! log

xy ! log

log

(

log

13.54log

ln!a $ b" $ ln!a ' b" ' 2 ln c

ln!1 $ x

" $

ln x ' ln sin x

ln 3 $

ln 8ln 5 $ 5 ln 3

ln!x $ y" $ ln!x ' y" ' 2 ln z

log

a ' log

b $ log

!x $ 1"

ln!uv"

1. (a) How is the logarithmic function deﬁned?

(b) What is the domain of this function?

(d) Sketch the general shape of the graph of the function

if .

2. (a) What is the natural logarithm?

(b) What is the common logarithm?

the natural exponential function with a common set of

axes.

3– 8 Find the exact value of each expression.

3. (a) (b)

4. (a) (b)

5. (a) (b)

6. (a) (b)

7. (a)

(b)

8. (a) (b)

9–12 Use the properties of logarithms to expand the quantity.

9. 10. ln

a!b

$ c

log

(

ln e

)

'2 ln 5

log

100 ' log

18 ' log

log

6 ' log

15 $ log

log

320 ' log

5log

0.1

ln 15

log

ln!1#e"

log

125

a " 1y ! log

y ! log

E X E R C I S E S

7.3

loudness, in decibels (dB), of a sound with intensity is then

deﬁned to be . Ampliﬁed rock music is

measured at 120 dB, whereas the noise from a motor-driven

lawn mower is measured at 106 dB. Find the ratio of the inten-

sity of the rock music to that of the mower.

43.

If a bacteria population starts with 100 bacteria and doubles

every three hours, then the number of bacteria after hours

is .

(a) Find the inverse of this function and explain its meaning.

(b) When will the population reach 50,000?

44.

When a camera ﬂash goes off, the batteries immediately begin

to recharge the ﬂash’s capacitor, which stores electric charge

given by

(The maximum charge capacity is and is measured in

seconds.)

(a) Find the inverse of this function and explain its meaning.

(b) How long does it take to recharge the capacitor to 90% of

capacity if ?

45–50

Find the limit.

45. 46.

48.

49.

50.

51–52

Find the domain of the function.

51. 52.

53–54

Find (a) the domain of and (b) and its domain.

53. 54.

55–60

Find the inverse function.

55. 56.

58.

59. 60.

61.

On what interval is the function increasing?

62. On what interval is the curve concave

downward?

63. On what intervals is the curve concave

upward?

y ! !x

' 2"e

y ! 2e

' e

'3x

f !x" ! e

' e

y !

1 $ 2e

y ! log

1 $

x # 1y ! !ln x"

f !x" ! e

57.

y ! 2

y ! ln!x $ 3"

f!x" ! ln!2 $ ln x"f!x" !

3 ' e

f !x" ! ln x $ ln!2 ' x"f !x" ! log

' 9"

lim

x l !

$ln!2 $ x" ' ln!1 $ x"%

lim

$ln!1 $ x

" ' ln!1 $ x"%

lim

ln!sin x"lim

ln!cos x"

47.

lim

log

!8x ' x

"lim

ln!x

' 9"

a ! 2

Q!t" ! Q

!1 ' e

't#a

n ! f !t" ! 100 % 2

t#3

L ! 10 log

!I#I

23–24

Make a rough sketch of the graph of each function. Do not

use a calculator. Just use the graphs given in Figures 2 and 3 and,

if necessary, the transformations of Section 1.3.

(a) (b)

24.

(a) (b)

25–34

Solve each equation for .

25.

(a) (b)

26.

(a) (b)

28.

(a) (b)

29. 30.

31. 32.

33.

35 –36

Find the solution of the equation correct to four decimal

places.

35.

(a) (b)

36.

(a) (b)

37–38

Solve each inequality for .

37.

(a) (b)

38.

(a) (b)

Suppose that the graph of is drawn on a coordinate

grid where the unit of measurement is an inch. How many

miles to the right of the origin do we have to move before the

height of the curve reaches ft?

40.

The velocity of a particle that moves in a straight line under the

inﬂuence of viscous forces is , where and are

positive constants.

(a) Show that the acceleration is proportional to the velocity.

(b) Explain the signiﬁcance of the number .

41.

The geologist C. F. Richter deﬁned the magnitude of an

earthquake to be , where is the intensity of the

quake (measured by the amplitude of a seismograph 100 km

from the epicenter) and is the intensity of a “standard”

earthquake (where the amplitude is only 1 micron cm).

The 1989 Loma Prieta earthquake that shook San Francisco

had a magnitude of 7.1 on the Richter scale. The 1906 San

Francisco earthquake was 16 times as intense. What was its

magnitude on the Richter scale?

42.

A sound so faint that it can just be heard has intensity

watt#m at a frequency of 1000 hertz (Hz). The

! 10

'12

! 10

Ilog

!I#S "

!t" ! ce

'kt

y ! log

39.

2'3x

" 4

ln x

ln x " '1

1#!x'4"

! 7ln

(

1 $

)

! 2

ln!e

' 2" ! 3e

2$5x

! 100

ln!2x $ 1" ! 2 ' ln x

34.

' e

' 6 ! 0

! 10ln!ln x" ! 1

10!1 $ e

! 33xe

$ x

! 0

log

!mx" ! c

3x$1

! k

ln x $ ln!x ' 1" ! 12

x'5

! 3

27.

ln!5 ' 2x" ! '3e

2x$ 3

' 7 ! 0

! 52 ln x ! 1

y ! ln

)

y ! ln!'x"

y ! 'ln xy ! log

!x $ 5"

23.

410

|| ||

CHAPTER 7 INVERSE FUNCTIONS

Openmirrors.com

then

71. Solve the inequality .

72. A prime number is a positive integer that has no factors

other than 1 and itself. The ﬁrst few primes are , , , , ,

, , . . . . We denote by the number of primes that are

less than or equal to . For instance, because there

are six primes smaller than 15.

(a) Calculate the numbers and .

[Hint: To ﬁnd , ﬁrst compile a list of the primes up

to 100 using the sieve of Eratosthenes: Write the numbers

from 2 to 100 and cross out all multiples of 2. Then cross

out all multiples of 3. The next remaining number is 5, so

cross out all remaining multiples of it, and so on.]

(b) By inspecting tables of prime numbers and tables of loga-

rithms, the great mathematician K. F. Gauss made the

guess in 1792 (when he was 15) that the number of

primes up to is approximately when is large.

More precisely, he conjectured that

This was ﬁnally proved, a hundred years later, by Jacques

Hadamard and Charles de la Vallée Poussin and is called

the Prime Number Theorem. Provide evidence for the

truth of this theorem by computing the ratio of to

for , , , , , and . Use the

following data: , ,

, , .

of primes up to a billion.

(

!10

" ! 664,579

(

!10

" ! 78,498

(

!10

" ! 9592

(

!10

" ! 1229

(

!1000" ! 168

1000n ! 100n#ln n

(

!n"

lim

n l !

(

!n"

n#ln n

! 1

nn#ln nn

(

!100"

(

!100"

(

!25"

(

!15" ! 6n

(

!n"1713

117532

ln!x

' 2x ' 2" & 0

ln x

0.1

0.1x " Nif

;

64. For the period from 1980 to 2000, the percentage of house-

holds in the United States with at least one VCR has been

modeled by the function

where the time is measured in years since midyear 1980, so

. Use a graph to estimate the time at which the

number of VCRs was increasing most rapidly. Then use

derivatives to give a more accurate estimate.

65. (a) Show that the function is an

odd function.

(b) Find the inverse function of .

66. Find an equation of the tangent to the curve that is

perpendicular to the line .

67. Show that the equation has no solution. What can

you say about the function ?

68. Any function of the form , where ,

can be analyzed as a power of by writing so

that . Using this device, calculate each limit.

(a) (b)

69. Let . Prove, using Deﬁnitions 4.4.6 and 4.4.7, that

(a) (b)

;

70. (a) Compare the rates of growth of and

by graphing both and in several viewing

rectangles. When does the graph of ﬁnally surpass the

graph of ?

(b) Graph the function in a viewing rect-

angle that displays the behavior of the function as .x l !

h!x" ! !ln x"#x

0.1

tft!x" ! ln x

f !x" ! x

0.1

lim

! !lim

! 0

a " 1

lim

!ln 2x"

'ln x

lim

1#x

lim

'ln x

lim

ln x

f !x" ! e

h!x" ln t!x"

t!x" ! e

ln t!x"

t!x" " 0f !x" ! $ t!x"%

h!x"

f !x" ! x

1#ln x

1# ln x

! 2

2x ' y ! 8

y ! e

f !x" ! ln

(

x $

$ 1

)

0 & t & 20

V!t" !

1 $ 53e

'0.5t

SECTION 7.4 DERIVATIVES OF LOGARITHMIC FUNCTIONS

|| ||

411

DER IVATIV ES O F LO GARI THM I C FU NCT I ONS

In this section we ﬁnd the derivatives of the logarithmic functions and the expo-

nential functions . We start with the natural logarithmic function . We know

that it is differentiable because it is the inverse of the differentiable function .

PROOF Let . Then

! x

y ! ln x

!ln x" !

y ! e

y ! ln xy ! a

y ! log

7.4