Stewart J. Calculus

Differentiating this equation implicitly with respect to , we get

and so

M

EXAMPLE 1 Differentiate .

SOLUTION To use the Chain Rule, we let . Then , so

M

In general, if we combine Formula 1 with the Chain Rule as in Example 1, we get

or

EXAMPLE 2 Find .

SOLUTION Using (2), we have

M

EXAMPLE 3 Differentiate .

SOLUTION This time the logarithm is the inner function, so the Chain Rule gives

M

EXAMPLE 4 Find .

SOLUTION 1

SOLUTION 2

If we ﬁrst simplify the given function using the laws of logarithms, then the

differentiation becomes easier:

!

1

x $ 1

'

1

2

&

1

x ' 2

'

d

dx

ln

x $ 1

s

x ' 2

!

d

dx

[

ln!x $ 1" '

1

2

ln!x ' 2"

]

!

x ' 2 '

1

2

!x $ 1"

!x $ 1"!x ' 2"

!

x ' 5

2!x $ 1"!x ' 2"

!

s

x ' 2

x $ 1

s

x ' 2

% 1 ' !x $ 1"

(

1

2

)

!x ' 2"

'1#2

x ' 2

d

dx

ln

x $ 1

s

x ' 2

!

1

x $ 1

s

x ' 2

d

dx

x $ 1

s

x ' 2

d

dx

ln

x $ 1

s

x ' 2

f )!x" !

1

2

!ln x"

'1#2

d

dx

!ln x" !

1

2

s

ln x

"

1

x

!

1

2x

s

ln x

f !x" !

s

ln x

d

dx

ln!sin x" !

1

sin x

d

dx

!sin x" !

1

sin x

cos x ! cot x

d

dx

ln!sin x"

V

d

dx

$ln t!x"% !

t)!x"

t!x"

d

dx

!ln u" !

1

u

du

dx

2

dy

dx

!

dy

du

dx

!

1

u

du

dx

!

1

x

3

$ 1

!3x

2

" !

3x

2

x

3

$ 1

y ! ln uu ! x

3

$ 1

y ! ln!x

3

$ 1"

V

dy

dx

!

1

e

y

!

1

x

e

y

dy

dx

! 1

x

412

|| ||

CHAPTER 7 INVERSE FUNCTIONS

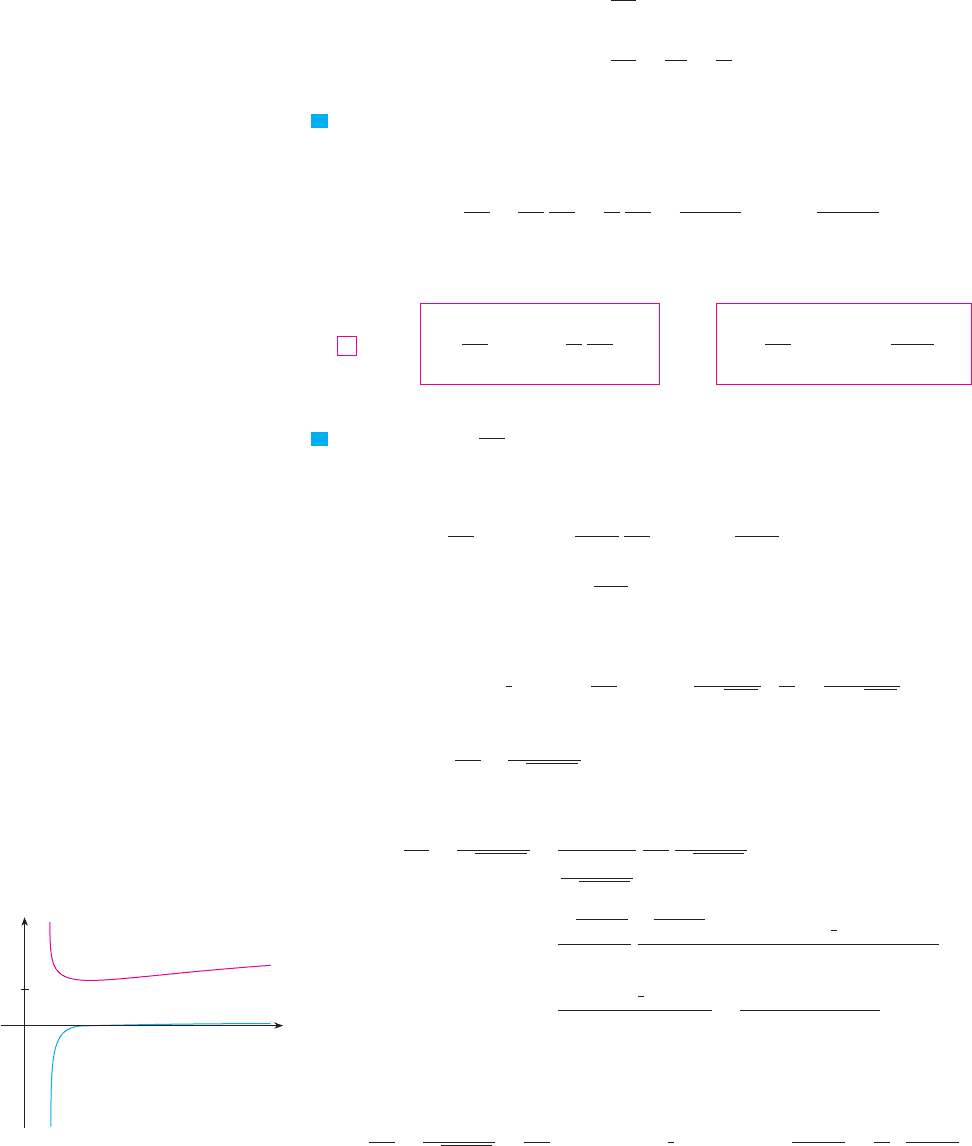
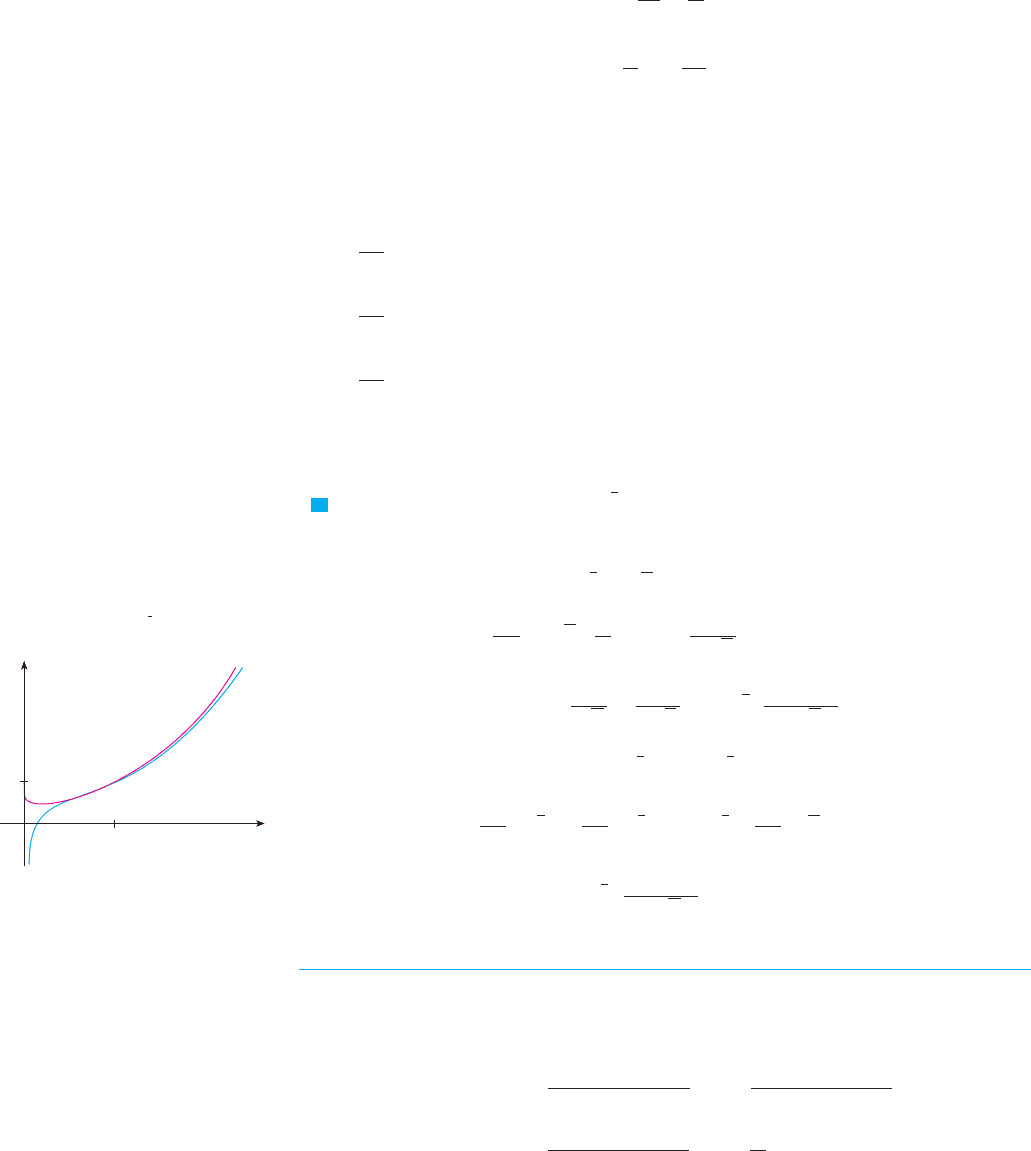
N Figure 1 shows the graph of the function

of Example 4 together with the graph of its deriv-

ative. It gives a visual check on our calculation.

Notice that is large negative when is

rapidly decreasing and when has

a minimum.

ff )!x" ! 0

ff )!x"

f

x

0

y

1

f

fª

F I G U R E 1

(This answer can be left as written, but if we used a common denominator we would see

that it gives the same answer as in Solution 1.) M

EXAMPLE 5 Find the absolute minimum value of .

SOLUTION The domain is and the Product Rule gives

Therefore when , that is, , or . Also,

when and for . So, by the First Derivative Test for

Absolute Extreme Values, is the absolute minimum.

M

EXAMPLE 6 Discuss the curve using the guidelines of Section 4.5.

SOLUTION

A. The domain is

B. The -intercept is . To ﬁnd the -intercept we set

We know that (since ), so we have

and therefore the -intercepts are .

C. Since , is even and the curve is symmetric about the -axis.

D. We look for vertical asymptotes at the endpoints of the domain. Since

as and also as , we have

and

by (7.3.8). Thus the lines and are vertical asymptotes.

E.

Since when and when , is increasing

on and decreasing on .

F. The only critical number is . Since changes from positive to negative at ,

is a local maximum by the First Derivative Test.

G.

Since for all , the curve is concave downward on and has no

inﬂection point.

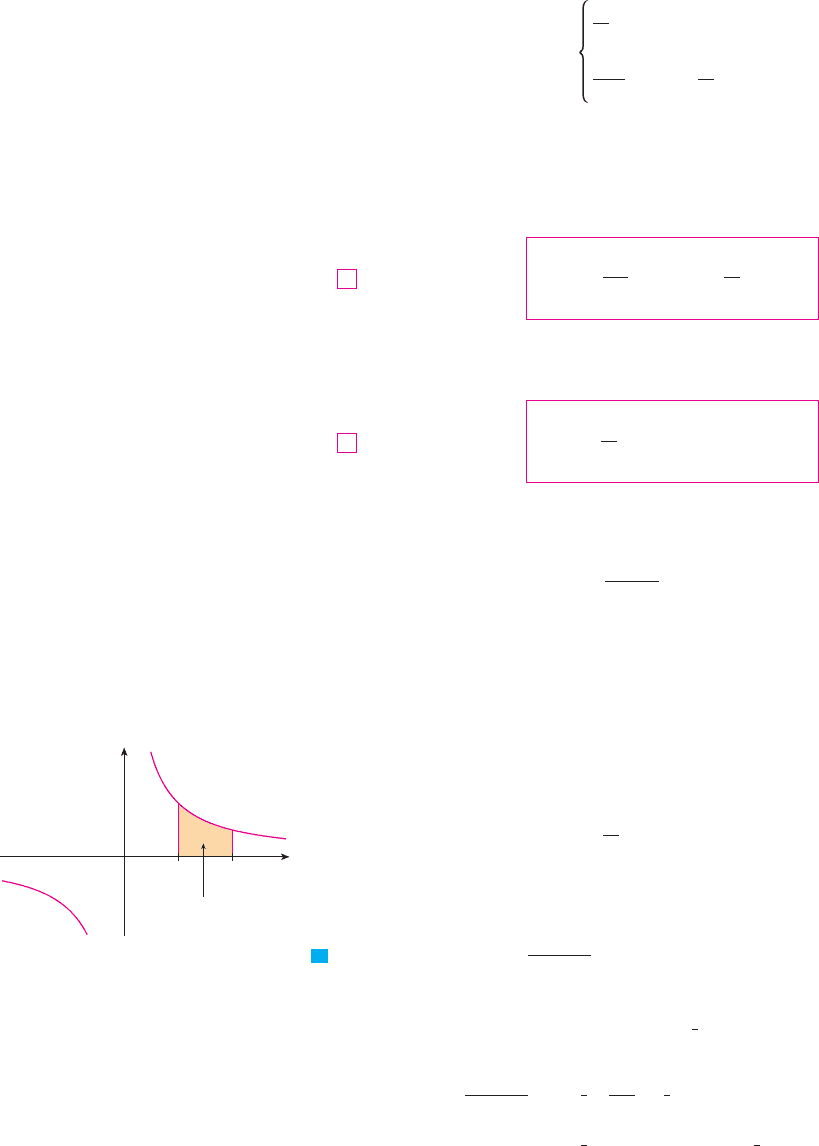
H. Using this information, we sketch the curve in Figure 2. M

EXAMPLE 7 Find if .

SOLUTION Since

f !x" !

*

ln x

ln!'x"

if x " 0

if x

-

0

f !x" ! ln

)

x

)

f )!x"

V

!'2, 2"x

f *!x"

-

0

f *!x" !

!4 ' x

2

"!'2" $ 2x!'2x"

!4 ' x

2

"

2

!

'8 ' 2x

2

!4 ' x

2

"

2

f !0" ! ln 4

0f )x ! 0

!0, 2"!'2, 0"

f

0

-

x

-

2f )!x"

-

0'2

-

x

-

0

f )!x" " 0

f )!x" !

'2x

4 ' x

2

x ! '2x ! 2

lim

x

l

'2

$

ln!4 ' x

2

" ! '!lim

x

l

2

'

ln!4 ' x

2

" ! '!

x l '2

$

x l 2

'

4 ' x

2

l 0

$

yff !'x" ! f !x"

.

s

3

x

4 ' x

2

! 1 ? x

2

! 3e

0

! 1ln 1 ! log

e

1 ! 0

y ! ln!4 ' x

2

" ! 0

xf !0" ! ln 4y

+x

)

4 ' x

2

" 0, ! +x

)

x

2

-

4, ! +x

)

x

)

-

2, ! !'2, 2"

y ! ln!4 ' x

2

"

f

(

1#

s

e

)

! '1#!2e"

0

-

x

-

e

'1#2

f )!x"

-

0x " e

'1#2

f )!x" " 0x ! e

'1#2

ln x ! '

1

2

2 ln x ! '1f )!x" ! 0

f )!x" ! x

2

"

1

x

$ 2x ln x ! x!1 $ 2 ln x"

!0, !"

f !x" ! x

2

ln x

SECTION 7.4 DERIVATIVES OF LOGARITHMIC FUNCTIONS

|| ||

413

{œ„3,0}

{_œ„3,0}

0

y

x

x=2x=_2

(0,ln4)

F I G U R E 2

y

=ln(4 -≈)

it follows that

Thus for all .

M

The result of Example 7 is worth remembering:

The corresponding integration formula is

Notice that this ﬁlls the gap in the rule for integrating power functions:

The missing case is supplied by Formula 4.

EXAMPLE 8 Find, correct to three decimal places, the area of the region under the

hyperbola from to .

SOLUTION The given region is shown in Figure 3. Using Formula 4 (without the absolute

value sign, since ), we see that the area is

M

EXAMPLE 9 Evaluate .

SOLUTION We make the substitution because the differential occurs

(except for the constant factor 2). Thus and

!

1

2

ln

!

x

2

! 1

!

! C !

1

2

ln"x

2

! 1# ! C

y

x

2

! 1

dx !

1

2

y

du

u

!

1

2

ln

!

u

!

! C

x dx !

1

2

du

du ! 2x dxu ! x

2

! 1

y

x

2

! 1

dx

V

! ln 2 " ln 1 ! ln 2 $ 0.693

A !

y

2

1

x

dx ! ln x

]

1

2

x # 0

x ! 2x ! 1xy ! 1

"n ! "1#

if n " "1

y

x

n

dx !

x

n!1

n ! 1

! C

y

1

x

dx ! ln

!

x

!

! C

4

d

dx

(

ln

!

x

!

)

!

1

x

3

x " 0f $"x# ! 1%x

1

x

if x # 0

1

"x

""1# !

1

x

if x

%

0

f $"x# !

414

|| ||

CHAPTER 7 INVERSE FUNCTIONS

F I G U R E 3

0

y

t

1 2

y=∆

area=ln2

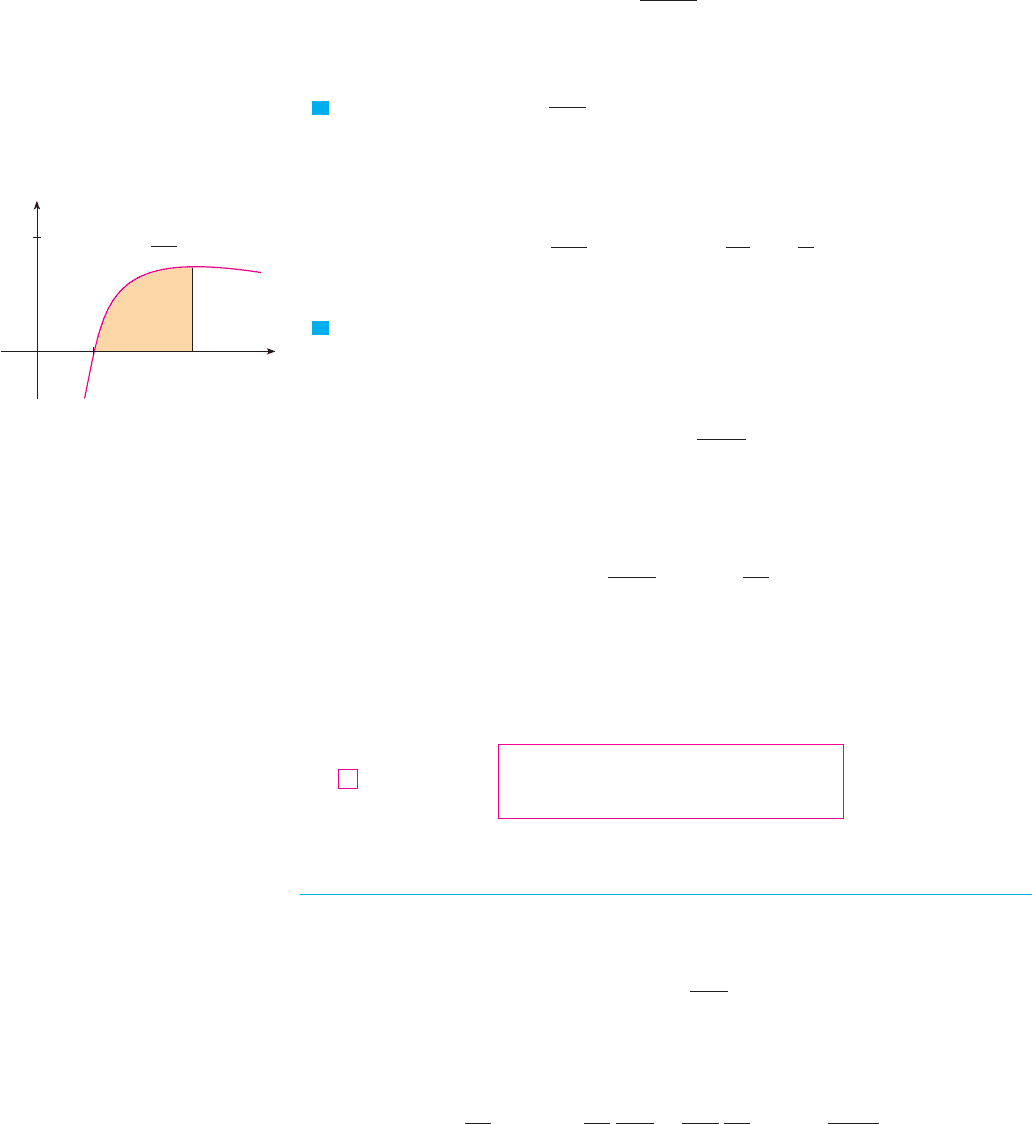
Notice that we removed the absolute value signs because for all . We could

use the properties of logarithms to write the answer as

but this isn’t necessary.

M

EXAMPLE 10 Calculate .

SOLUTION We let because its differential occurs in the integral. When

, ; when , . Thus

M

EXAMPLE 11 Calculate .

SOLUTION First we write tangent in terms of sine and cosine:

This suggests that we should substitute since then and so

:

M

Since , the result of Example 11 can also be

written as

GENERAL LOGARIT H M I C AN D E X P O NE N T I AL FU N C T I ON S

Formula 7 in Section 7.3 expresses a logarithmic function with base in terms of the nat-

ural logarithmic function:

Since is a constant, we can differentiate as follows:

d

dx

"log

a

x# !

d

dx

ln x

ln a

!

1

ln a

d

dx

"ln x# !

1

x ln a

ln a

log

a

x !

ln x

ln a

a

y

tan x dx ! ln

!

sec x

!

! C

5

"ln

!

cos x

!

! ln"1%

!

cos x

!

# ! ln

!

sec x

!

! "ln

!

u

!

! C ! "ln

!

cos x

!

! C

y

tan x dx !

y

sin x

cos x

dx ! "

y

du

u

sin x dx ! "du

du ! "sin x dxu ! cos x

y

tan x dx !

y

sin x

cos x

dx

y

tan x dx

V

y

e

1

ln x

x

dx !

y

1

0

u du !

u

2

&

0

1

!

1

2

u ! ln e ! 1x ! eu ! ln 1 ! 0x ! 1

du ! dx%xu ! ln x

y

e

1

ln x

x

dx

V

ln

s

x

2

! 1 ! C

xx

2

! 1 # 0

SECTION 7.4 DERIVATIVES OF LOGARITHMIC FUNCTIONS

|| ||

415

x

0

y

0.5

1

e

y=

lnx

x

F I G U R E 4

N Since the function in

Example 10 is positive for , the integral

represents the area of the shaded region in

Figure 4.

x # 1

f "x# ! "ln x#%x

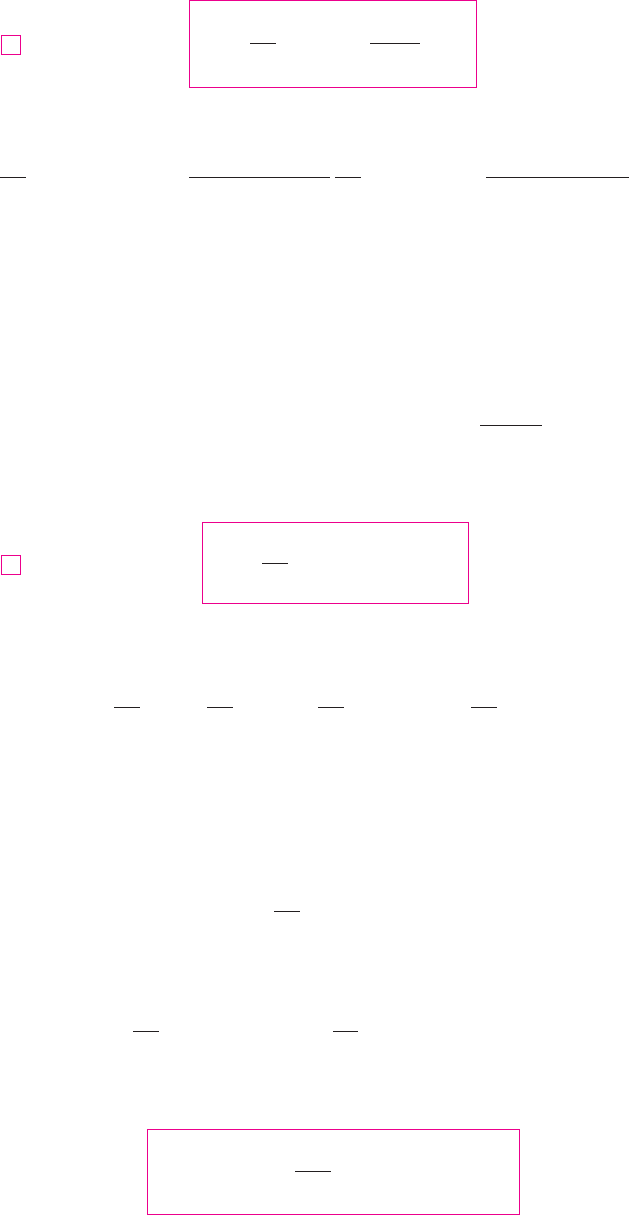
EXAMPLE 12 Using Formula 6 and the Chain Rule, we get

M

From Formula 6 we see one of the main reasons that natural logarithms (logarithms

with base ) are used in calculus: The differentiation formula is simplest when

because .

EXPONENTIAL FUNCTIONS WITH BASE In Section 7.2 we showed that the derivative

of the general exponential function , is a constant multiple of itself:

We are now in a position to show that the value of the constant is .

PROOF We use the fact that :

M

In Example 6 in Section 3.7 we considered a population of bacteria cells that doubles

every hour and we saw that the population after hours is , where is the initial

population. Formula 7 enables us to ﬁnd the growth rate:

EXAMPLE 13 Combining Formula 7 with the Chain Rule, we have

M

The integration formula that follows from Formula 7 is

a " 1

y

a

x

dx !

a

x

ln a

! C

d

dx

(

10

x

2

)

! 10

x

2

"ln 10#

d

dx

"x

2

# ! "2 ln 10#x10

x

2

dn

dt

! n

0

2

t

ln 2

n

0

n ! n

0

2

t

! "e

ln a

#

x

"ln a# ! a

x

ln a

d

dx

"a

x

# !

d

dx

"e

ln a

#

x

!

d

dx

e

"ln a#x

! e

"ln a#x

d

dx

"ln a#x

e

ln a

! a

d

dx

"a

x

# ! a

x

ln a

7

f $"0# ! ln a

f $"0# ! lim

h l 0

a

h

" 1

h

wheref $"x# ! f $"0#a

x

f "x# ! a

x

, a # 0

a

ln e ! 1

a ! ee

d

dx

log

10

"2 ! sin x# !

1

"2 ! sin x# ln 10

d

dx

"2 ! sin x# !

cos x

"2 ! sin x# ln 10

d

dx

"log

a

x# !

1

x ln a

6

416

|| ||

CHAPTER 7 INVERSE FUNCTIONS

EXAMPLE 14 M

LOGARITHMI C DIF F E R E NT I ATION

The calculation of derivatives of complicated functions involving products, quotients, or

powers can often be simpliﬁed by taking logarithms. The method used in the following

example is called logarithmic differentiation.

EXAMPLE 15 Differentiate .

SOLUTION We take logarithms of both sides of the equation and use the properties of loga-

rithms to simplify:

Differentiating implicitly with respect to gives

Solving for , we get

Because we have an explicit expression for , we can substitute and write

M

STEPS IN LOGARITHMIC DIFFERENTIATION

1.

Take natural logarithms of both sides of an equation and use the

properties of logarithms to simplify.

2. Differentiate implicitly with respect to .

3. Solve the resulting equation for .

If for some values of , then is not deﬁned, but we can write

and use Equation 3. We illustrate this procedure by proving the general ver-

sion of the Power Rule, as promised in Section 3.3.

THE POWER RULE If is any real number and , then

PROOF Let and use logarithmic differentiation:

x " 0ln

!

y

!

! ln

!

x

!

n

! n ln

!

x

!

y ! x

n

f $"x# ! nx

n"1

f "x# ! x

n

!

y

!

f "x#

!

ln f "x#xf "x#

%

0

y$

x

y ! f "x#

dy

dx

!

x

3%4

s

x

2

! 1

"3x ! 2#

5

'

3

4x

!

x

2

! 1

"

15

3x ! 2

(

y

dy

dx

! y

'

3

4x

!

x

2

! 1

"

15

3x ! 2

(

dy%dx

1

y

dy

dx

!

3

4

!

1

x

!

1

2

!

2x

x

2

! 1

" 5 !

3

3x ! 2

x

ln y !

3

4

ln x !

1

2

ln"x

2

! 1# " 5 ln"3x ! 2#

y !

x

3%4

s

x

2

! 1

"3x ! 2#

5

y

5

0

2

x

dx !

2

x

ln 2

&

0

5

!

2

5

ln 2

"

2

0

ln 2

!

31

ln 2

SECTION 7.4 DERIVATIVES OF LOGARITHMIC FUNCTIONS

|| ||

417

N If we hadn’t used logarithmic differentiation in

Example 15, we would have had to use both the

Quotient Rule and the Product Rule. The resulting

calculation would have been horrendous.

N If , we can show that for

directly from the deﬁnition of a derivative.n # 1

f $"0# ! 0x ! 0

Therefore

Hence M

|

You should distinguish carefully between the Power Rule , where

the base is variable and the exponent is constant, and the rule for differentiating exponen-

tial functions , where the base is constant and the exponent is variable.

In general there are four cases for exponents and bases:

1. ( and are constants)

2.

3.

4.

To ﬁnd , logarithmic differentiation can be used, as in the next

example.

EXAMPLE 16 Differentiate .

SOLUTION 1 Using logarithmic differentiation, we have

SOLUTION 2 Another method is to write :

(as in Solution 1) M

THE NUMBER

e

AS A LIMIT

We have shown that if , then . Thus . We now use this fact

to express the number as a limit.

From the deﬁnition of a derivative as a limit, we have

! lim

x l 0

ln"1 ! x#

1%x

! lim

x l 0

ln"1 ! x# " ln 1

x

! lim

x l 0

1

x

ln"1 ! x#

f $"1# ! lim

h l 0

f "1 ! h# " f "1#

h

! lim

x l 0

f "1 ! x# " f "1#

x

e

f $"1# ! 1f $"x# ! 1%xf "x# ! ln x

! x

s

x

'

2 ! ln x

2

s

x

(

d

dx

(

x

s

x

)

!

d

dx

(

e

s

x

ln x

)

! e

s

x

ln x

d

dx

(

s

x

ln x

)

x

s

x

! "e

ln x

#

s

x

y$ ! y

'

1

s

x

!

ln x

2

s

x

(

! x

s

x

'

2 ! ln x

2

s

x

(

y$

y

!

s

x

!

1

x

! "ln x#

1

2

s

x

ln y ! ln x

s

x

!

s

x

ln x

y ! x

s

x

V

"d%dx#) f "x#*

t"x#

d

dx

)a

t"x#

* ! a

t"x#

"ln a#t$"x#

d

dx

) f "x#*

b

! b) f "x#*

b"1

f $"x#

ba

d

dx

"a

b

# ! 0

)"d%dx# a

x

! a

x

ln a*

)"d%dx# x

n

! nx

n"1

*

y$ ! n

y

x

! n

x

n

x

! nx

n"1

y$

y

!

n

x

418

|| ||

CHAPTER 7 INVERSE FUNCTIONS

N Figure 5 illustrates Example 16 by showing

the graphs of and its derivative.f "x# ! x

s

x

F I G U R E 5

1

f

fª

x

0

y

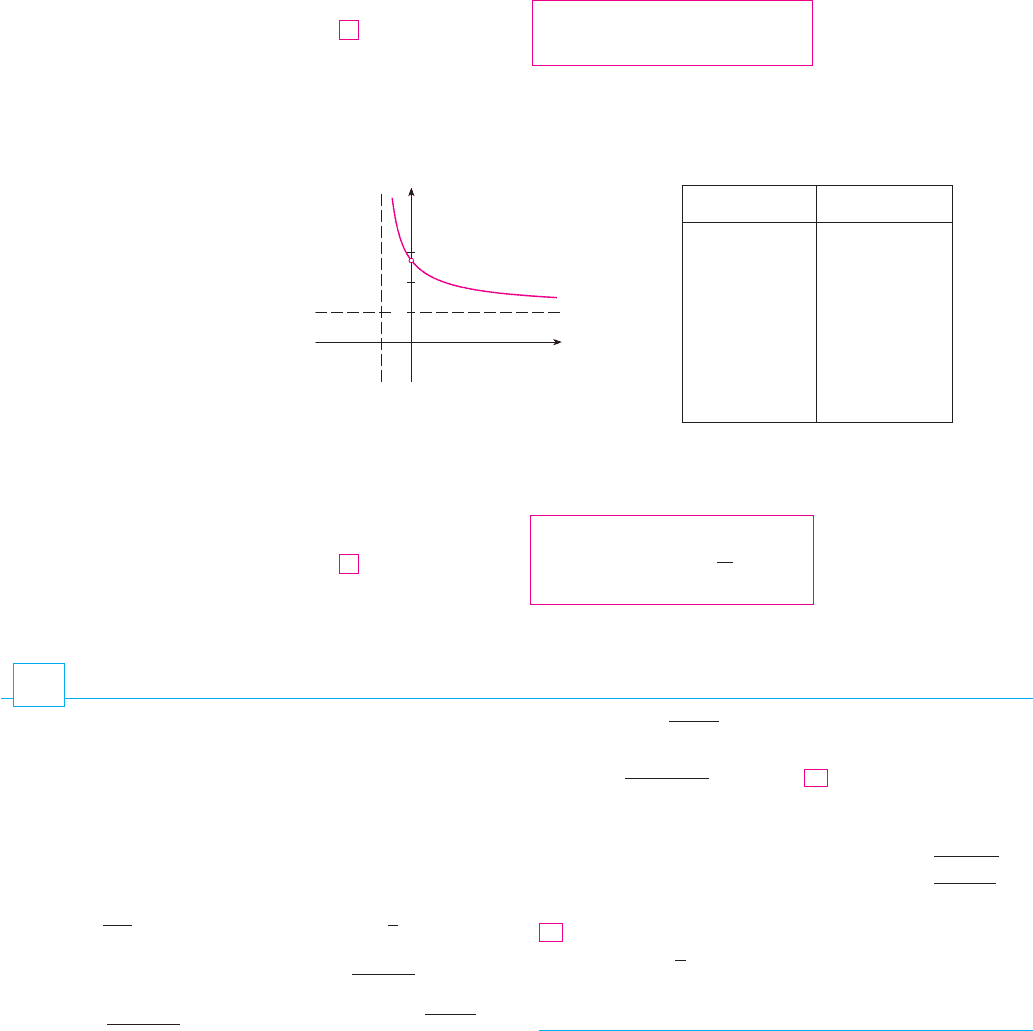
Because , we have

Then, by Theorem 2.5.8 and the continuity of the exponential function, we have

Formula 8 is illustrated by the graph of the function in Figure 6 and a

table of values for small values of .

If we put in Formula 8, then as and so an alternative expression

for is

e ! lim

n l &

'

1 !

1

n

(

n

9

e

x l 0

!

n l &n ! 1%x

F I G U R E 6

2

3

y=(1+x)!?®

1

0

y

x

y ! "1 ! x#

1%x

e ! lim

x l 0

"1 ! x#

1%x

8

e ! e

1

! e

lim

x

l

0

ln"1!x#

1%x

! lim

x

l

0

e

ln"1!x#

1%x

! lim

x

l

0

"1 ! x#

1%x

lim

x

l

0

ln"1 ! x#

1%x

! 1

f $"1# ! 1

SECTION 7.4 DERIVATIVES OF LOGARITHMIC FUNCTIONS

|| ||

419

x

0.1 2.59374246

0.01 2.70481383

0.001 2.71692393

0.0001 2.71814593

0.00001 2.71826824

0.000001 2.71828047

0.0000001 2.71828169

0.00000001 2.71828181

(1 ! x)

1/x

13. 14.

15.

17. 18.

19. 20.

22.

23. 24.

25. 26.

y ! 2

3

x

2

y ! 5

"1%x

y ! log

2

"e

"x

cos

'

x#y ! 2x log

10

s

x

y ! )ln"1 ! e

x

#*

2

y ! ln"e

"x

! xe

"x

#

21.

H"z# ! ln

+

a

2

" z

2

a

2

! z

2

y ! ln

!

2 " x " 5x

2

!

y ! 10

tan

(

h"t# ! t

3

" 3

t

y ! ln"x

4

sin

2

x#

16.

f "u# !

ln u

1 ! ln"2u#

F"y# ! y ln"1 ! e

y

#t"x# ! ln

(

x

s

x

2

" 1

)

1. Explain why the natural logarithmic function is used

much more frequently in calculus than the other logarithmic

functions .

2–26 Differentiate the function.

2.

3. 4.

5. 6.

7. 8.

9. 10.

11. 12.

h"x# ! ln

(

x !

s

x

2

" 1

)

F"t# ! ln

"2t ! 1#

3

"3t " 1#

4

f "t# !

1 ! ln t

1 " ln t

f "x# ! sin x ln"5x#

f "x# ! ln

s

5

x

f "x# !

s

5

ln x

f "x# ! log

5

"xe

x

#f "x# ! log

2

"1 " 3x#

f "x# ! ln"sin

2

x#f "x# ! sin"ln x#

f "x# ! ln"x

2

! 10#

y ! log

a

x

y ! ln x

E X E R C I S E S

7.4

Find the intervals of concavity and the inﬂection points of the

function .

60. Find the absolute minimum value of the function

.

61–64 Discuss the curve under the guidelines of Section 4.5.

61. 62.

63. 64.

65. If , use the graphs of , , and to

estimate the intervals of increase and the inﬂection points of

on the interval .

;

66. Investigate the family of curves . What

happens to the inﬂection points and asymptotes as changes?

Graph several members of the family to illustrate what you

discover.

;

67. The ﬂash unit on a camera operates by storing charge on a

capacitor and releasing it suddenly when the ﬂash is set off.

The following data describe the charge remaining on the

capacitor (measured in microcoulombs, )C) at time (mea-

sured in seconds).

(a) Use a graphing calculator or computer to ﬁnd an expo-

nential model for the charge.

(b) The derivative represents the electric current (mea-

sured in microamperes, )A) ﬂowing from the capacitor to

the ﬂash bulb. Use part (a) to estimate the current when

s. Compare with the result of Example 2 in

Section 2.1.

;

68. The table gives the US population from 1790 to 1860.

(a) Use a graphing calculator or computer to ﬁt an exponen-

tial function to the data. Graph the data points and the

exponential model. How good is the ﬁt?

(b) Estimate the rates of population growth in 1800 and 1850

by averaging slopes of secant lines.

(c) Use the exponential model in part (a) to estimate the rates

of growth in 1800 and 1850. Compare these estimates

with the ones in part (b).

t ! 0.04

Q$"t#

t

Q

c

f "x# ! ln"x

2

! c#

"0, 15*f

f *f $ff "x# ! ln"2x ! x sin x#

CAS

y ! ln"x

2

" 3x ! 2#y ! ln"1 ! x

2

#

y ! ln"tan

2

x#y ! ln"sin x#

f "x# ! x ln x

f "x# ! "ln x#%

s

x

59.

27–30 Find and .

27. 28.

29. 30.

31–34 Differentiate and ﬁnd the domain of .

32.

33. 34.

35. If , ﬁnd .

36. If , ﬁnd .

37–38 Find an equation of the tangent line to the curve at the

given point.

37. , 38.

;

39. If , ﬁnd . Check that your answer is

reasonable by comparing the graphs of and .

;

40. Find equations of the tangent lines to the curve

at the points and . Illustrate by graphing the

curve and its tangent lines.

41–52 Use logarithmic differentiation to ﬁnd the derivative of the

function.

41. 42.

43. 44.

46.

48.

49. 50.

51. 52.

53. Find if .

Find if .

55. Find a formula for if .

56. Find .

;

57–58 Use a graph to estimate the roots of the equation correct

to one decimal place. Then use these estimates as the initial

approximations in Newton’s method to ﬁnd the roots correct to

six decimal places.

57. 58.

ln"4 " x

2

# ! x"x " 4#

2

! ln x

d

9

dx

9

"x

8

ln x#

f "x# ! ln"x " 1#f

"n#

"x#

x

y

! y

x

y$

54.

y ! ln"x

2

! y

2

#y$

y ! "ln x#

cos x

y ! "tan x#

1%x

y ! "sin x#

ln x

y ! "cos x#

x

y !

s

x

y ! x

sin x

47.

y ! x

cos x

y ! x

x

45.

y !

+

4

x

2

! 1

x

2

" 1

y !

sin

2

x tan

4

x

"x

2

! 1#

2

y !

s

x

e

x

2

"x

2

! 1#

10

y ! "2x ! 1#

5

"x

4

" 3#

6

"e, 1%e#"1, 0#

y ! "ln x#%x

f $f

f $"x#f "x# ! sin x ! ln x

y ! ln"x

3

" 7#, "2, 0#"1, 1#y ! ln

(

xe

x

2

)

f $"0#f "x# ! ln"1 ! e

2x

#

f $"1#f "x# !

ln x

1 ! x

2

f "x# ! ln ln ln xf "x# ! ln"x

2

" 2x#

f "x# !

1

1 ! ln x

f "x# !

x

1 " ln"x " 1#

31.

ff

y ! ln"sec x ! tan x#y ! ln

(

x !

s

1 ! x

2

)

y ! "ln x#%x

2

y ! x

2

ln"2x#

y*y$

420

|| ||

CHAPTER 7 INVERSE FUNCTIONS

t 0.00 0.02 0.04 0.06 0.08 0.10

Q 100.00 81.87 67.03 54.88 44.93 36.76

Year Population Year Population

1790 3,929,000 1830 12,861,000

1800 5,308,000 1840 17,063,000

1810 7,240,000 1850 23,192,000

1820 9,639,000 1860 31,443,000

SECTION 7.2* THE NATURAL LOGARITHMIC FUNCTION

|| ||

421

84. Find the volume of the solid obtained by rotating the region

under the curve

from 0 to 3 about the -axis.

85. The work done by a gas when it expands from volume

to volume is , where is the

pressure as a function of the volume . (See Exercise 27 in

Section 6.4.) Boyle’s Law states that when a quantity of gas

expands at constant temperature, , where is a con-

stant. If the initial volume is 600 and the initial pressure

is 150 kPa, ﬁnd the work done by the gas when it expands at

constant temperature to 1000 .

86. Find if , , , and .

87. If is the inverse function of , ﬁnd .

88. If and , ﬁnd .

89. For what values of do the line and the curve

enclose a region? Find the area of the region.

;

90. (a) Find the linear approximation to near l.

(b) Illustrate part (a) by graphing and its linearization.

(c) For what values of is the linear approximation accurate

to within 0.1?

Use the deﬁnition of derivative to prove that

92. Show that for any .x # 0lim

n l &

'

1 !

x

n

(

n

! e

x

lim

x

l

0

ln"1 ! x#

x

! 1

91.

x

f

f "x# ! ln x

y ! x%"x

2

! 1#

y ! mxm

h$"e#h"x# ! f

"1

"x#f "x# ! e

x

! ln x

t$"2#f "x# ! 2x ! ln xt

f "2# ! 0f "1# ! 0x # 0f *"x# ! x

"2

f

cm

3

cm

3

CPV ! C

V

P ! P"V #W !

x

V

2

V

1

P dVV

2

V

1

y

y !

1

x

2

! 1

(d) Use the exponential model to predict the population in

1870. Compare with the actual population of 38,558,000.

Can you explain the discrepancy?

69– 80 Evaluate the integral.

69. 70.

71. 72.

73. 74.

76.

77. 78.

79. 80.

81. Show that by (a) differentiating

the right side of the equation and (b) using the method of

Example 11.

82. Find, correct to three decimal places, the area of the region

above the hyperbola , below the -axis, and

between the lines and .

83. Find the volume of the solid obtained by rotating the region

under the curve

from 0 to 1 about the -axis.x

y !

1

s

x ! 1

x ! "1x ! "4

xy ! 2%"x " 2#

x cot x dx ! ln

!

sin x

!

! C

y

x2

x

2

dx

y

2

1

10

t

dt

y

e

x

e

x

! 1

dx

y

sin 2x

1 ! cos

2

x

dx

y

cos x

2 ! sin x

dx

y

"ln x#

2

x

dx

75.

y

sin"ln x#

x

dx

y

e

1

x

2

! x ! 1

x

dx

y

9

4

'

s

x

!

1

s

x

(

2

dx

y

2

1

dt

8 " 3t

y

2

1

4 ! u

2

u

3

du

y

4

2

3

x

dx

THE NATURAL L OGA RITH MIC FU NCTI ON

In this section we deﬁne the natural logarithm as an integral and then show that it obeys

the usual laws of logarithms. The Fundamental Theorem makes it easy to differentiate this

function.

DEFINITION The natural logarithmic function is the function deﬁned by

The existence of this function depends on the fact that the integral of a continuous func-

tion always exists. If , then can be interpreted geometrically as the area under ln xx # 1

x # 0ln x !

y

x

1

t

dt

1

7.2*

N If your instructor has assigned Sections

7.2–7.4, you need not read Sections 7.2*, 7.3*,

and 7.4* (pp. 421–446).

Stewart J. Calculus

Подождите немного. Документ загружается.