Stewart J. Calculus

Подождите немного. Документ загружается.

Since the natural logarithm is found on scientiﬁc calculators, we can approximate the

solution to four decimal places: . M

The exponential function is one of the most frequently occurring functions

in calculus and its applications, so it is important to be familiar with its graph (Figure 2)

and its properties (which follow from the fact that it is the inverse of the natural logarith-

mic function).

PROPERTIES OF THE NATURAL EXPONENTIAL FUNCTION The exponential func-

tion is an increasing continuous function with domain and range

. Thus for all . Also

So the -axis is a horizontal asymptote of .

EXAMPLE 3 Find .

SOLUTION We divide numerator and denominator by :

We have used the fact that as and so

We now verify that has the properties expected of an exponential function.

LAWS OF EXPONENTS If and are real numbers and is rational, then

1. 2. 3.

PROOF OF LAW 1 Using the ﬁrst law of logarithms and Equation 5, we have

Since is a one-to-one function, it follows that

Laws 2 and 3 are proved similarly (see Exercises 95 and 96). As we will see in the

next section, Law 3 actually holds when is any real number.

! e

x"y

.ln

ln"e

# ! ln"e

# " ln"e

# ! x " y ! ln"e

x"y

! e

x$y

x"y

! e

ryx

f "x# ! e

lim

x l #

$2x

! lim

t l $#

! 0

x l #t ! $2x l $#

1 " 0

! 1

lim

" 1

! lim

1 " e

$2x

1 " lim

$2x

lim

x l #

" 1

f "x# ! e

lim

x l $#

! 0 lim

x l #

! #

& 0"0, ##

!f "x# ! e

f "x# ! e

x % 0.8991

432

|| ||

CHAPTER 7 INVERSE FUNCTIONS

y=´

F I G U R E 2

The natural exponential function

DIFFERENTIATION

The natural exponential function has the remarkable property that it is its own derivative.

PROOF

The function is differentiable because it is the inverse function of ,

which we know is differentiable with nonzero derivative. To ﬁnd its derivative, we use

the inverse function method. Let . Then and, differentiating this latter

equation implicitly with respect to , we get

The geometric interpretation of Formula 8 is that the slope of a tangent line to the curve

at any point is equal to the -coordinate of the point (see Figure 3). This property

implies that the exponential curve grows very rapidly (see Exercise 100).

EXAMPLE 4

Differentiate the function .

SOLUTION

To use the Chain Rule, we let . Then we have , so

In general, if we combine Formula 8 with the Chain Rule, as in Example 4, we get

EXAMPLE 5

Find if .

SOLUTION

Using Formula 9 and the Product Rule, we have

EXAMPLE 6

Find the absolute maximum value of the function .

SOLUTION

We differentiate to ﬁnd any critical numbers:

Since exponential functions are always positive, we see that when ,

that is, when . Similarly, when . By the First Derivative Test for

Absolute Extreme Values, has an absolute maximum value when and the value is

f "1# ! "1#e

% 0.37

x ! 1f

x & 1f !"x#

1 $ x & 0f !"x# & 0

f !"x# ! xe

"$1# " e

"1# ! e

"1 $ x#

f "x# ! xe

y! ! e

$4x

"cos 5x#"5# " "sin 5x#e

$4x

"$4# ! e

$4x

"5 cos 5x $ 4 sin 5x#

y ! e

$4x

sin 5xy!

# ! e

! e

tan x

sec

y ! e

u ! tan x

y ! e

tan x

y ! e

yy ! e

! y ! e

! 1

ln y ! xy ! e

y ! ln xy ! e

# ! e

SECTION 7.3* THE NATURAL EXPONENTIAL FUNCTION

|| ||

433

F I G U R E 3

slope=1

slope=e®

y=e®

{x,e®}

Visual 7.2 /7.3* uses the slope-a-

scope to illustrate this formula.

TE C

Openmirrors.com

EXAMPLE 7 Use the ﬁrst and second derivatives of , together with asymp-

totes, to sketch its graph.

SOLUTION Notice that the domain of is , so we check for vertical asymptotes

by computing the left and right limits as . As , we know that ,

and this shows that is a vertical asymptote. As , we have ,

As , we have and so

This shows that is a horizontal asymptote.

Now let’s compute the derivative. The Chain Rule gives

Since and for all , we have for all . Thus is

decreasing on and on . There is no critical number, so the function has no

maximum or minimum. The second derivative is

Since and , we have when and

when . So the curve is concave downward on and concave upward on

and on . The inﬂection point is .

To sketch the graph of we ﬁrst draw the horizontal asymptote (as a dashed

line), together with the parts of the curve near the asymptotes in a preliminary sketch

[Figure 4(a)]. These parts reﬂect the information concerning limits and the fact that is

decreasing on both and . Notice that we have indicated that as

even though does not exist. In Figure 4(b) we ﬁnish the sketch by incorpo-

rating the information concerning concavity and the inﬂection point. In Figure 4(c) we

check our work with a graphing device.

(a) Preliminary sketch (b) Finished sketch

F I G U R E 4

_3 3

y=1

y=‰

inﬂection

point

y=1

f !0"x l 0

f !x" l 0!0, ""!!", 0"

y ! 1f

(

, e

)

!0, ""

(

, 0

)

(

!", !

)

f $!x"

0!x " 0"x % !

f $!x" % 0x

% 0e

1#x

% 0

f $!x" ! !

1#x

!!1#x

" ! e

1#x

!2x"

1#x

!2x & 1"

!0, ""!!", 0"

fx " 0f '!x"

0x " 0x

% 0e

1#x

% 0

f '!x" ! !

1#x

y ! 1

lim

x l("

1#x

! e

! 1

1#x l 0x l ("

lim

1#x

! lim

! 0

t ! 1#x l !"x l 0

x ! 0

lim

1#x

! lim

! "

t ! 1#x l "x l 0

x l 0

x " 0&f

f !x" ! e

1#x

434

|| ||

CHAPTER 7 INVERSE FUNCTIONS

INTEGRATIO N

Because the exponential function has a simple derivative, its integral is also simple:

EXAMPLE 8 Evaluate .

SOLUTION We substitute . Then , so and

EXAMPLE 9 Find the area under the curve from 0 to l.

SOLUTION The area is

MA !

!3x

dx ! !

!3x

]

!1 ! e

y ! e

!3x

dx !

du !

& C !

& C

dx !

dudu ! 3x

dxu ! x

dx ! e

& C

y ! e

SECTION 7.3* THE NATURAL EXPONENTIAL FUNCTION

|| ||

435

16. (a) (b)

17–20 Make a rough sketch of the graph of the function. Do not

use a calculator. Just use the graph given in Figure 2 and, if neces-

sary, the transformations of Section 1.3.

17. 18.

20.

21–22 Find (a) the domain of and (b) and its domain.

21. 22.

23–26 Find the inverse function.

23. 24. ,

26.

27–32 Find the limit.

27. 28.

29. 30.

31. 32.

lim

)

#2"

tan x

lim

!2x

cos x"

lim

3#!2!x"

lim

3#!2!x"

lim

x l "

! e

!3x

& e

!3x

y !

1 & 2e

f !x" ! e

25.

x * 1y ! !ln x"

y ! ln!x & 3"

f!x" ! ln!2 & ln x"f ! x" !

3 ! e

y ! 2!1 ! e

"y ! 1 !

19.

y ! 1 & 2e

y ! e

2!3x

% 4

ln x

1. Sketch, by hand, the graph of the function with par-

ticular attention to how the graph crosses the y-axis. What fact

allows you to do this?

2– 4 Simplify each expression.

2. (a) (b)

3. (a) (b)

4. (a) (b)

5–12 Solve each equation for .

5. (a) (b)

6. (a) (b)

7. (a) (b)

8. (a) (b)

9. 10.

11.

13–14 Find the solution of the equation correct to four decimal

places.

13. (a) (b)

14. (a) (b)

15–16 Solve each inequality for .

15. (a) (b) ln x % !1

1#!x!4"

! 7ln

(

1 &

)

! 2

ln!e

! 2" ! 3e

2&5x

! 100

ln!2x & 1" ! 2 ! ln x

12.

! e

! 6 ! 0

10!1 & e

! 33xe

& x

! 0

! 10ln!ln x" ! 1

ln x & ln!x ! 1" ! 1e

3x&1

! k

ln!5 ! 2x" ! !3e

2x& 3

! 7 ! 0

! 52 ln x ! 1

x & ln x

ln e

sin x

(

ln e

)

!2 ln 5

ln!1#e"e

ln 15

f !x" ! e

E X E R C I S E S

7.3*

436

|| ||

CHAPTER 7 INVERSE FUNCTIONS

tion 10.4 we will see that this is a reasonable equation

for .]

(a) Find .

(b) Find the rate of spread of the rumor.

;

hours. Use the graph to estimate how long it will take for

80% of the population to hear the rumor.

;

62. For the period from 1980 to 2000, the percentage of house-

holds in the United States with at least one VCR has been

modeled by the function

where the time is measured in years since midyear 1980, so

. Use a graph to estimate the time at which the

number of VCRs was increasing most rapidly. Then use

derivatives to give a more accurate estimate.

63. Find the absolute maximum value of the function

64. Find the absolute minimum value of the function

, .

65–66 Find the absolute maximum and absolute minimum values

of on the given interval.

65. , 66. ,

67–68 Find (a) the intervals of increase or decrease, (b) the inter-

vals of concavity, and (c) the points of inﬂection.

67. 68.

69–70 Discuss the curve using the guidelines of Section 4.5.

70.

;

71. A drug response curve describes the level of medication in

the bloodstream after a drug is administered. A surge

function is often used to model the response

curve, reﬂecting an initial surge in the drug level and then a

more gradual decline. If, for a particular drug,

, and is measured in minutes, estimate the

times corresponding to the inﬂection points and explain their

signiﬁcance. If you have a graphing device, use it to graph

the drug response curve.

;

72–73 Draw a graph of that shows all the important aspects of

the curve. Estimate the local maximum and minimum values and

then use calculus to ﬁnd these values exactly. Use a graph of

to estimate the inﬂection points.

72. 73. f !x" ! e

f !x" ! e

cos x

f $

tp ! 4, k ! 0.07

A ! 0.01,

S!t" ! At

!kt

y ! e

2 x

! e

y ! e

!1#!x&1"

69.

f !x" !

f !x" ! !1 ! x"e

'!1, 6(f !x" ! x

!x#2

'!1, 4(f !x" ! xe

x % 0t!x" ! e

f !x" ! x ! e

0 + t + 20

V!t" !

1 & 53e

!0.5t

tk ! 0.5a ! 10p

lim

p!t"

33 – 48 Differentiate the function.

33. 34.

36.

37. 38.

40.

41. 42.

43. 44.

45. 46.

47. 48.

49–50 Find an equation of the tangent line to the curve at the

given point.

49.

Find if .

52. Find an equation of the tangent line to the curve

at the point .

53. Show that the function satisﬁes the differen-

tial equation .

54. Show that the function satisﬁes the differ-

ential equation .

55. For what values of does the function satisfy the

equation ?

56. Find the values of for which satisﬁes the equation

If , ﬁnd a formula for .

58. Find the thousandth derivative of .

59. (a) Use the Intermediate Value Theorem to show that there is

a root of the equation .

(b) Use Newton’s method to ﬁnd the root of the equation in

part (a) correct to six decimal places.

;

60. Use a graph to ﬁnd an initial approximation (to one decimal

place) to the root of the equation .

Then use Newton’s method to ﬁnd the root correct to eight

decimal places.

61. Under certain circumstances a rumor spreads according to the

equation

where is the proportion of the population that knows the

rumor at time and and are positive constants. [In Sec-

kat

p!t"

p!t" !

1 & ae

!k t

sin x ! x

! x & 1

& x ! 0

f !x" ! xe

!n"

!x"f !x" ! e

57.

y & y' ! y$

y ! e

y$ & 6y' & 8y ! 0

y ! e

y$ & 2y' & y ! 0

y ! Ae

& Bxe

2y$ ! y' ! y ! 0

y ! e

& e

! x / 2

!0, 1"xe

& ye

! 1

! x & yy'

51.

y ! e

#x, !1, e"

50.

y ! e

cos

)

x, !0, 1"

f !t" ! sin

sin

"y ! cos

)

1 ! e

1 & e

y !

1 & xe

!2x

y !

& b

& d

y !

! e

& e

y ! e

k tan

y !

1 & 2e

f !t" ! sin!e

" & e

sin t

F!t" ! e

t sin 2t

39.

t!x" !

f !u" ! e

1#u

y ! e

!cos u & cu"y ! e

35.

y !

1 & x

f !x" ! !x

& 2x"e

91. If , ﬁnd .

92. Evaluate .

;

93. If you graph the function

you’ll see that appears to be an odd function. Prove it.

;

94. Graph several members of the family of functions

where . How does the graph change when changes?

How does it change when changes?

95. Prove the second law of exponents [see (7)].

96. Prove the third law of exponents [see (7)].

97. (a) Show that if .

[Hint: Show that is increasing

for .]

(b) Deduce that .

98. (a) Use the inequality of Exercise 97(a) to show that, for

(b) Use part (a) to improve the estimate of given in

Exercise 97(b).

99. (a) Use mathematical induction to prove that for and

any positive integer ,

(b) Use part (a) to show that .

for any positive integer .

;

100. This exercise illustrates Exercise 99(c) for the case .

(a) Compare the rates of growth of and

by graphing both and in several viewing rectangles.

When does the graph of ﬁnally surpass the graph of ?

(b) Find a viewing rectangle that shows how the function

behaves for large .

if then

% 10

x % N

xh!x" ! e

t!x" ! e

f !x" ! x

k ! 10

lim

x l "

! "

e % 2.7

* 1 & x &

& - - - &

x * 0

* 1 & x &

x * 0,

+ x

dx + e

x % 0

f !x" ! e

! !1 & x"

x * 0e

* 1 & x

ba % 0

f !x" !

1 & ae

f !x" !

1 ! e

1#x

1 & e

1#x

lim

x l

)

sin x

! 1

x !

)

! f

"'!4"f !x" ! 3 & x & e

74. The family of bell-shaped curves

occurs in probability and statistics, where it is called the nor-

mal density function. The constant is called the mean and

the positive constant is called the standard deviation. For

simplicity, let’s scale the function so as to remove the factor

and let’s analyze the special case where .

So we study the function

(a) Find the asymptote, maximum value, and inﬂection points

of .

(b) What role does play in the shape of the curve?

;

same screen.

75– 84 Evaluate the integral.

75. 76.

78.

79. 80.

81. 82.

84.

85. Find, correct to three decimal places, the area of the region

bounded by the curves , , and .

86. Find if , , and .

87. Find the volume of the solid obtained by rotating about the

-axis the region bounded by the curves , , ,

and .

Find the volume of the solid obtained by rotating about the

-axis the region bounded by the curves , ,

, and .

89. The error function

is used in probability, statistics, and engineering.

(a) Show that .

(b) Show that the function satisﬁes the differ-

ential equation .

90. A bacteria population starts with 400 bacteria and grows at a

rate of bacteria per hour. How many

bacteria will there be after three hours?

r!t" ! !450.268"e

1.12567t

y' ! 2xy & 2#

)

y ! e

erf!x"

dt !

)

'erf!b" ! erf!a"(

erf!x" !

)

x ! 1x ! 0

y ! 0y ! e

88.

x ! 1

x ! 0y ! 0y ! e

f '!0" ! 2f !0" ! 1f $!x" ! 3e

& 5 sin xf !x"

x ! 1y ! e

y ! e

sin!e

" dx

83.

1#x

sin x e

cos x

!4 & e

& e

!1 & e

1 & e

77.

!3x

f !x" ! e

#!2

! 01#

(

)

y !

)

!!x!

#!2

SECTION 7.3* THE NATURAL EXPONENTIAL FUNCTION

|| ||

437

438

|| ||

CHAPTER 7 INVERSE FUNCTIONS

GEN ERAL LOG ARIT HMIC AND EXP ONEN TIA L FUN CTI ONS

In this section we use the natural exponential and logarithmic functions to study exponen-

tial and logarithmic functions with base .

GENERAL EXPONEN T I A L F U N C TI O N S

If and is any rational number, then by (4) and (7) in Section 7.3*,

Therefore, even for irrational numbers , we deﬁne

Thus, for instance,

The function is called the exponential function with base a. Notice that is

positive for all because is positive for all .

Deﬁnition 1 allows us to extend one of the laws of logarithms. We know that

when is rational. But if we now let be any real number we have, from

Deﬁnition 1,

Thus

The general laws of exponents follow from Deﬁnition 1 together with the laws of expo-

nents for .

LAWS OF EXPONENTS If and are real numbers and , , then

1. 2. 3. 4.

PROOF

1. Using Deﬁnition 1 and the laws of exponents for , we have

3. Using Equation 2 we obtain

The remaining proofs are left as exercises. M

! e

xy ln a

! a

! e

y ln!a

! e

yx ln a

! e

x ln a

y ln a

! a

x&y

! e

!x&y" ln a

! e

x ln a & y ln a

!ab"

! a

x!y

! a

x&y

! a

b % 0ayx

ln a

! r ln a for any real number r

ln a

! ln!e

r ln a

" ! r ln a

rrln!a

" ! r ln a

f !x" ! a

! e

3 ln 2

+ e

1.20

+ 3.32

! e

x ln a

! !e

ln a

! e

r ln a

ra % 0

a % 0

7.4*

The differentiation formula for exponential functions is also a consequence of

Deﬁnition 1:

PROOF M

Notice that if , then and Formula 4 simpliﬁes to a formula that we

already know: . In fact, the reason that the natural exponential function is

used more often than other exponential functions is that its differentiation formula is

simpler.

EXAMPLE 1 In Example 6 in Section 3.7 we considered a population of bacteria cells in

a homogeneous nutrient medium. We showed that if the population doubles every hour,

then the population after hours is

where is the initial population. Now we can use (4) to compute the growth rate:

For instance, if the initial population is cells, then the growth rate after two

hours is

EXAMPLE 2 Combining Formula 4 with the Chain Rule, we have

EXPONENTIA L GRA P H S

If , then , so , which shows that is increas-

ing (see Figure 1). If , then and so is decreasing (see Figure 2).

F I G U R E 1

y=a®, a>1

F I G U R E 2

y=a®,0<a<1

lim a®=0, lim a®=`

lim a®=`, lim a®=0

y ! a

ln a

y ! a

!d#dx" a

! a

ln a % 0ln a % 0a % 1

(

)

! 10

!ln 10"

" ! !2 ln 10"x10

! 4000 ln 2 + 2773 cells#h

t!2

! !1000"2

ln 2

t!2

! 1000

! n

ln 2

n ! n

!d#dx" e

! e

ln e ! 1a ! e

! a

ln a

" !

x ln a

" ! e

x ln a

!x ln a"

" ! a

ln a

SECTION 7.4* GENERAL LOGARITHMIC AND EXPONENTIAL FUNCTIONS

|| ||

439

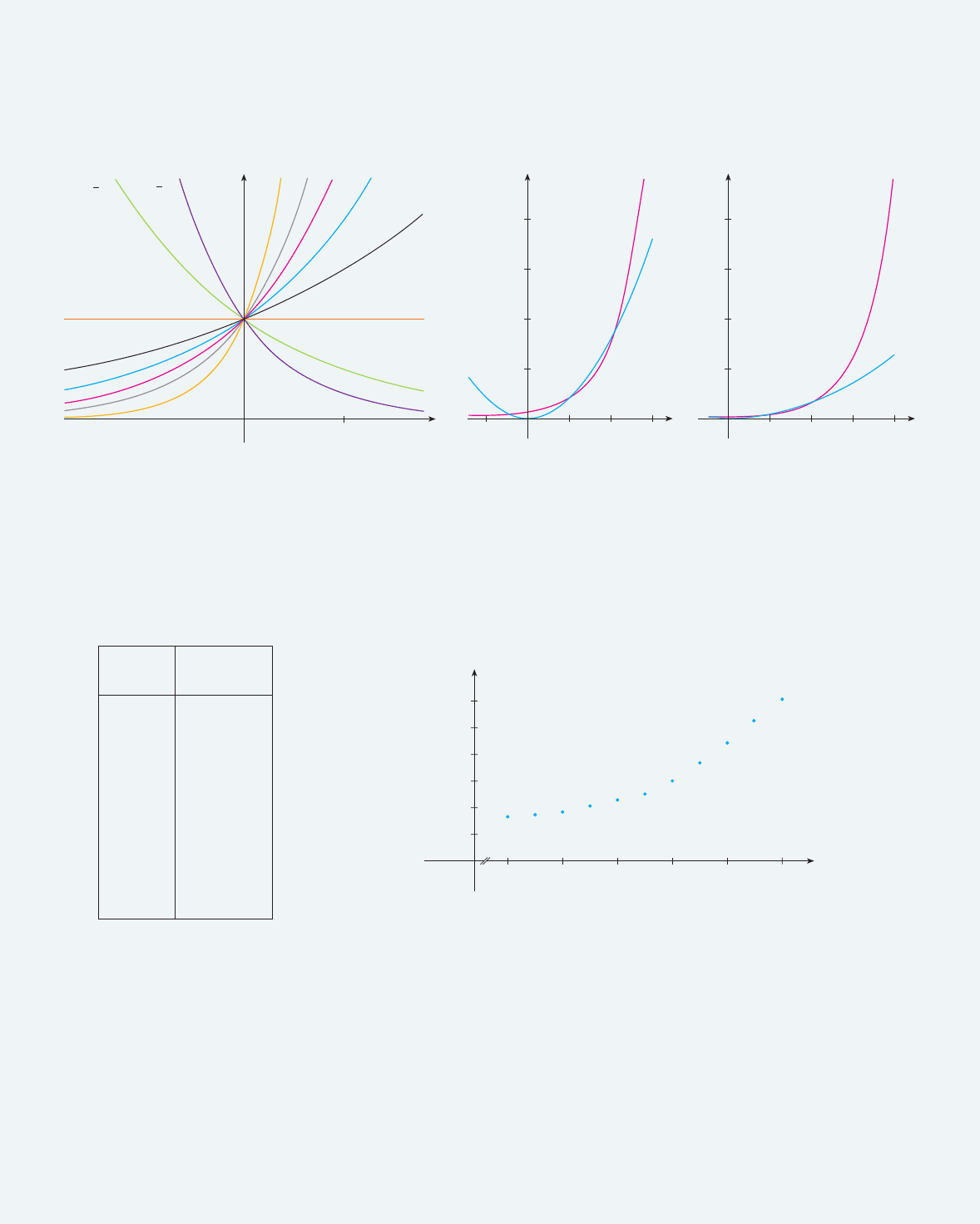
Notice from Figure 3 that as the base a gets larger, the exponential function grows more

rapidly (for ).

Figure 4 shows how the exponential function compares with the power function

. The graphs intersect three times, but ultimately the exponential curve

grows far more rapidly than the parabola . (See also Figure 5.)

In Section 7.5 we will show how exponential functions occur in the description of pop-

ulation growth and radioactive decay. Let’s look at human population growth. Table 1

shows data for the population of the world in the 20th century and Figure 6 shows the cor-

responding scatter plot.

The pattern of the data points in Figure 6 suggests exponential growth, so we use a

graphing calculator with exponential regression capability to apply the method of least

squares and obtain the exponential model

Figure 7 shows the graph of this exponential function together with the original data

points. We see that the exponential curve ﬁts the data reasonably well. The period of rela-

P ! !0.008079266" ! !1.013731"

F I G U R E 6 Scatter plot for world population growth

1900

6x10'

1920 1940 1960 1980 2000

y ! x

y ! 2

y ! x

y ! 2

F I G U R E 3

y=2®

y=≈

100

200

F I G U R E 5

y=2®

y=≈

F I G U R E 4

1.5®

1®

2®

4®

10®

”’

e®

x % 0

440

|| ||

CHAPTER 7 INVERSE FUNCTIONS

TA B L E 1

Population

Year (millions)

1900 1650

1910 1750

1920 1860

1930 2070

1940 2300

1950 2560

1960 3040

1970 3710

1980 4450

1990 5280

2000 6080

Members of the family of

exponential functions

tively slow population growth is explained by the two world wars and the Great Depres-

sion of the 1930s.

EXPONENTIA L INT E G R A LS

The integration formula that follows from Formula 4 is

EXAMPLE 3 M

THE POWE R RU L E VERSUS TH E E X P O N EN T I A L RULE

Now that we have deﬁned arbitrary powers of numbers, we are in a position to prove the

general version of the Power Rule, as promised in Section 3.3.

THE POWER RULE If is any real number and , then

PROOF Let and use logarithmic differentiation:

Therefore

Hence

You should distinguish carefully between the Power Rule , where

the base is variable and the exponent is constant, and the rule for differentiating exponen-

tial functions , where the base is constant and the exponent is variable.

'!d#dx" a

! a

ln a(

'!d#dx" x

! nx

n!1

(

y' ! n

! n

! nx

n!1

x " 0ln

! ln

! n ln

y ! x

f '!x" ! nx

n!1

f !x" ! x

dx !

ln 2

a " 1

dx !

ln a

& C

F I G U R E 7

Exponential model for

population growth

1900

6x10'

1920 1940 1960 1980 2000

SECTION 7.4* GENERAL LOGARITHMIC AND EXPONENTIAL FUNCTIONS

|| ||

441

N If , we can show that for

directly from the deﬁnition of a derivative.

n % 1

f '!0" ! 0x ! 0