Stewart J. Calculus
Подождите немного. Документ загружается.

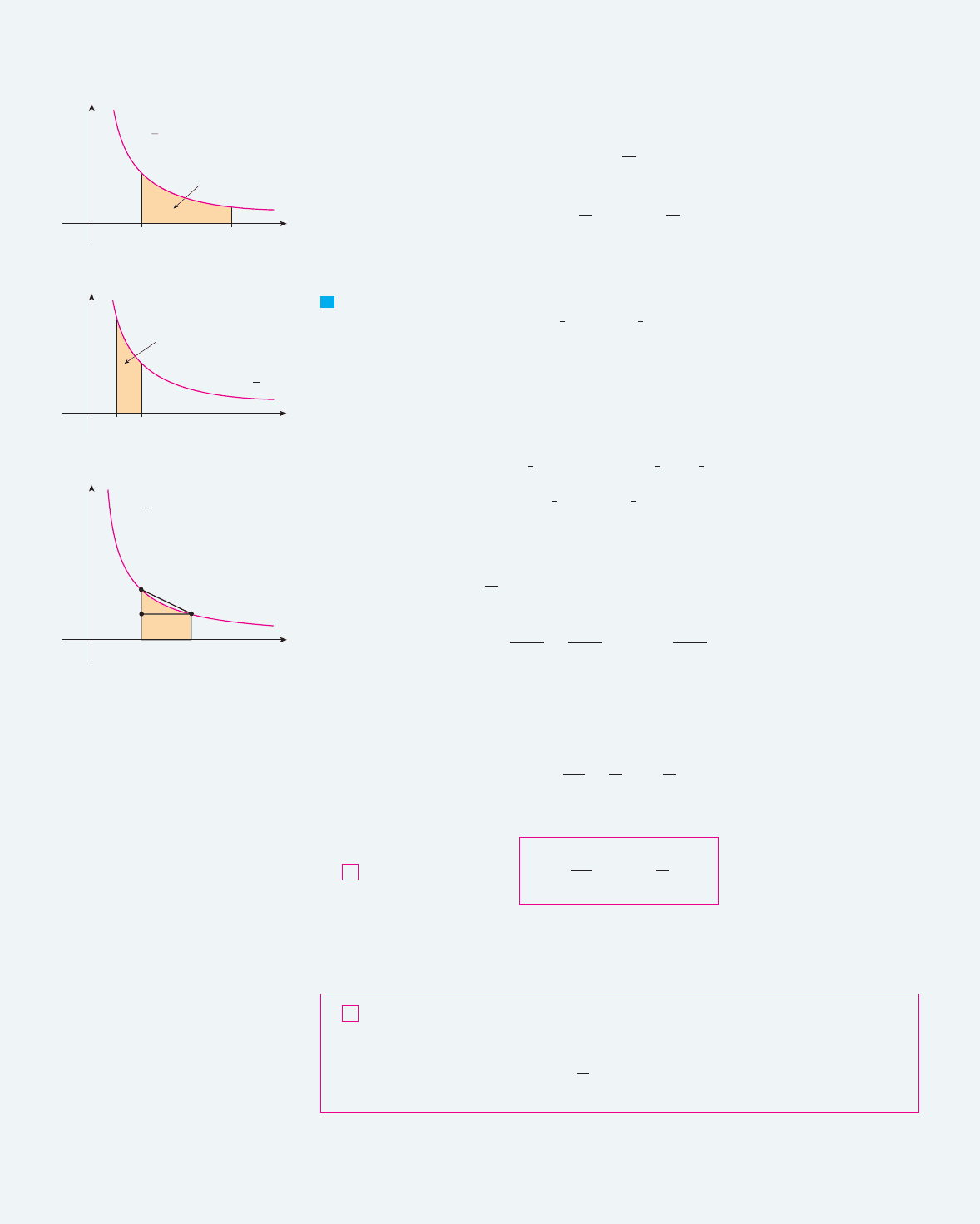
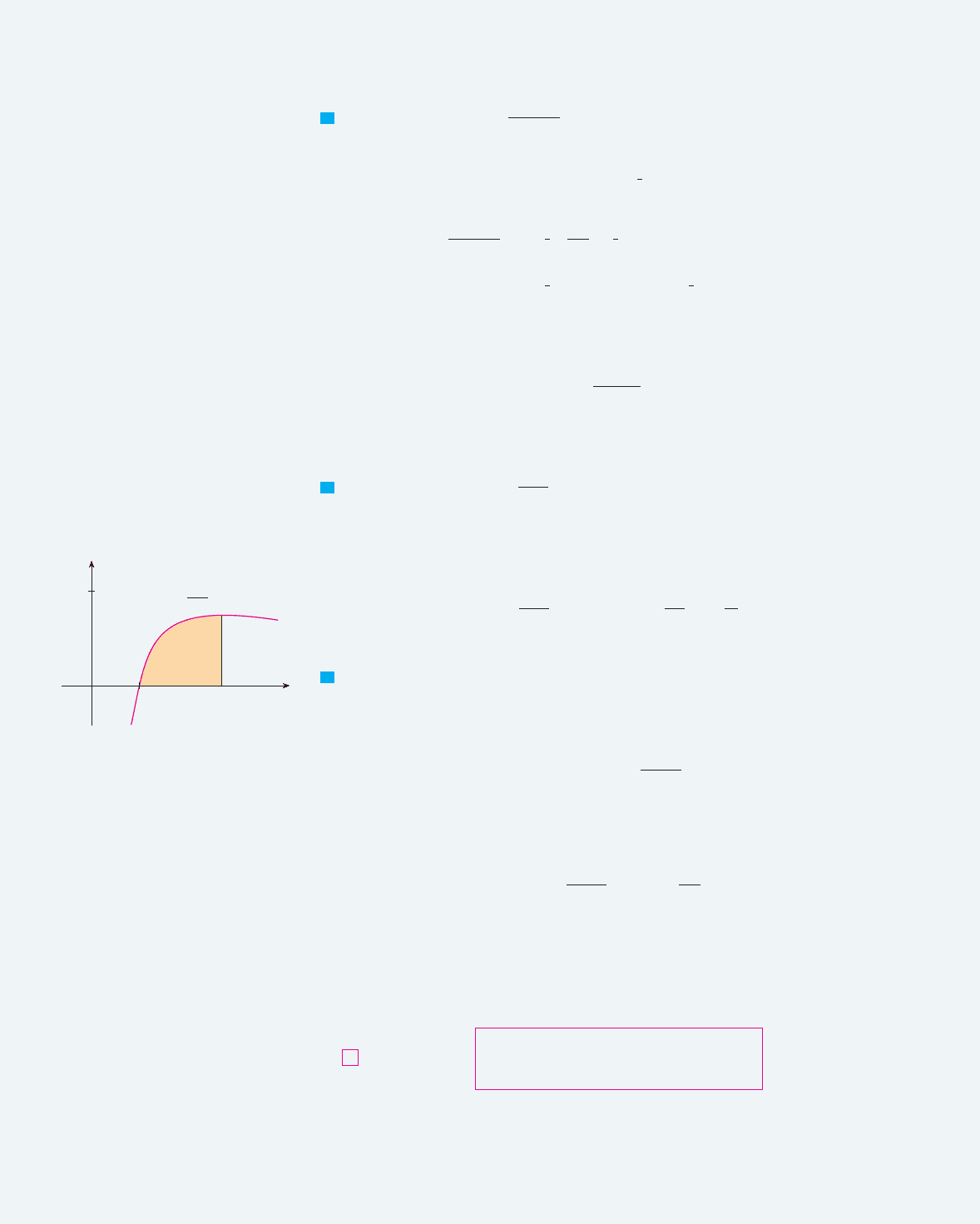
the hyperbola from to . (See Figure 1.) For , we have
For ,
and so is the negative of the area shown in Figure 2.
EXAMPLE 1
(a) By comparing areas, show that .
(b) Use the Midpoint Rule with to estimate the value of .
SOLUTION
(a) We can interpret as the area under the curve from 1 to 2. From Figure 3
we see that this area is larger than the area of rectangle and smaller than the area
of trapezoid . Thus we have
(b) If we use the Midpoint Rule with , and , we get
M
Notice that the integral that defines is exactly the type of integral discussed in Part 1
of the Fundamental Theorem of Calculus (see Section 5.3). In fact, using that theorem,
we have
and so
We now use this differentiation rule to prove the following properties of the logarithm
function.
LAWS OF LOGARITHMS If and are positive numbers and is a rational
number, then
1. 2. 3.
ln"x
r
# ! r ln xln
'
x
y
(
! ln x " ln yln"xy# ! ln x ! ln y
ryx
3
d
dx
"ln x# !
1
x
2
d
dx
y
x
1
1
t
dt !
1
x
ln x
! "0.1#
'
1
1.05
!
1
1.15
! + + + !
1
1.95
(
$ 0.693
ln 2 !
y
2
1
1
t
dt $ "0.1#) f "1.05# ! f "1.15# ! + + + ! f "1.95#*
,t ! 0.1f "t# ! 1%t, n ! 10
1
2
%
ln 2
%
3
4
1
2
! 1
%
ln 2
%
1 !
1
2
(
1 !
1
2
)
ABCD
BCDE
y ! 1%tln 2
ln 2n ! 10
1
2
%
ln 2
%
3
4
V
ln x
ln x !
y
x
1
1
t
dt ! "
y
1
x
1
t
dt
%
00
%
x
%
1
ln 1 !
y
1
1
1
t
dt ! 0
x ! 1t ! xt ! 1y ! 1%t
422
|| ||
CHAPTER 7 INVERSE FUNCTIONS
F I G U R E 2
F I G U R E 1
F I G U R E 3
y=
1
t
0
y
1 x
t
area=lnx
y=
1
t
0
y
1x
t
area=_lnx
y=
1
t
0
y
1 2
t
A
B
C
D
E
PROOF
1. Let , where is a positive constant. Then, using Equation 2 and the
Chain Rule, we have
Therefore and have the same derivative and so they must differ by a constant:
Putting in this equation, we get . Thus
If we now replace the constant by any number , we have
2. Using Law 1 with , we have
and so
Using Law 1 again, we have
The proof of Law 3 is left as an exercise. M
EXAMPLE 2 Expand the expression .
SOLUTION Using Laws 1, 2, and 3, we get
M
EXAMPLE 3 Express as a single logarithm.
SOLUTION Using Laws 3 and 1 of logarithms, we have
M
In order to graph , we first determine its limits:
(a) (b)
lim
x
l
0
!
ln x ! "&lim
x l &
ln x ! &
4
y ! ln x
! ln
(
a
s
b
)
! ln a ! ln
s
b
ln a !
1
2
ln b ! ln a ! ln b
1%2
ln a !
1
2
ln b
V
! 4 ln"x
2
! 5# ! ln sin x " ln"x
3
! 1#
ln
"x
2
! 5#
4
sin x
x
3
! 1
! ln"x
2
! 5#
4
! ln sin x " ln"x
3
! 1#
ln
"x
2
! 5#
4
sin x
x
3
! 1
ln
'
x
y
(
! ln
'
x !
1
y
(
! ln x ! ln
1
y
! ln x " ln y
ln
1
y
! "ln y
ln
1
y
! ln y ! ln
'
1
y
! y
(
! ln 1 ! 0
x ! 1%y
ln"xy# ! ln x ! ln y
ya
ln"ax# ! ln x ! ln a
ln a ! ln 1 ! C ! 0 ! C ! Cx ! 1
ln"ax# ! ln x ! C
ln xf "x#
f $"x# !
1
ax
d
dx
"ax# !
1
ax
! a !
1
x
af "x# ! ln"ax#
SECTION 7.2* THE NATURAL LOGARITHMIC FUNCTION
|| ||
423

PROOF
(a) Using Law 3 with and (where n is any positive integer), we have
. Now , so this shows that as . But is an
increasing function since its derivative is positive. Therefore as .
(b) If we let , then as . Thus, using (a), we have
M
If , then
and
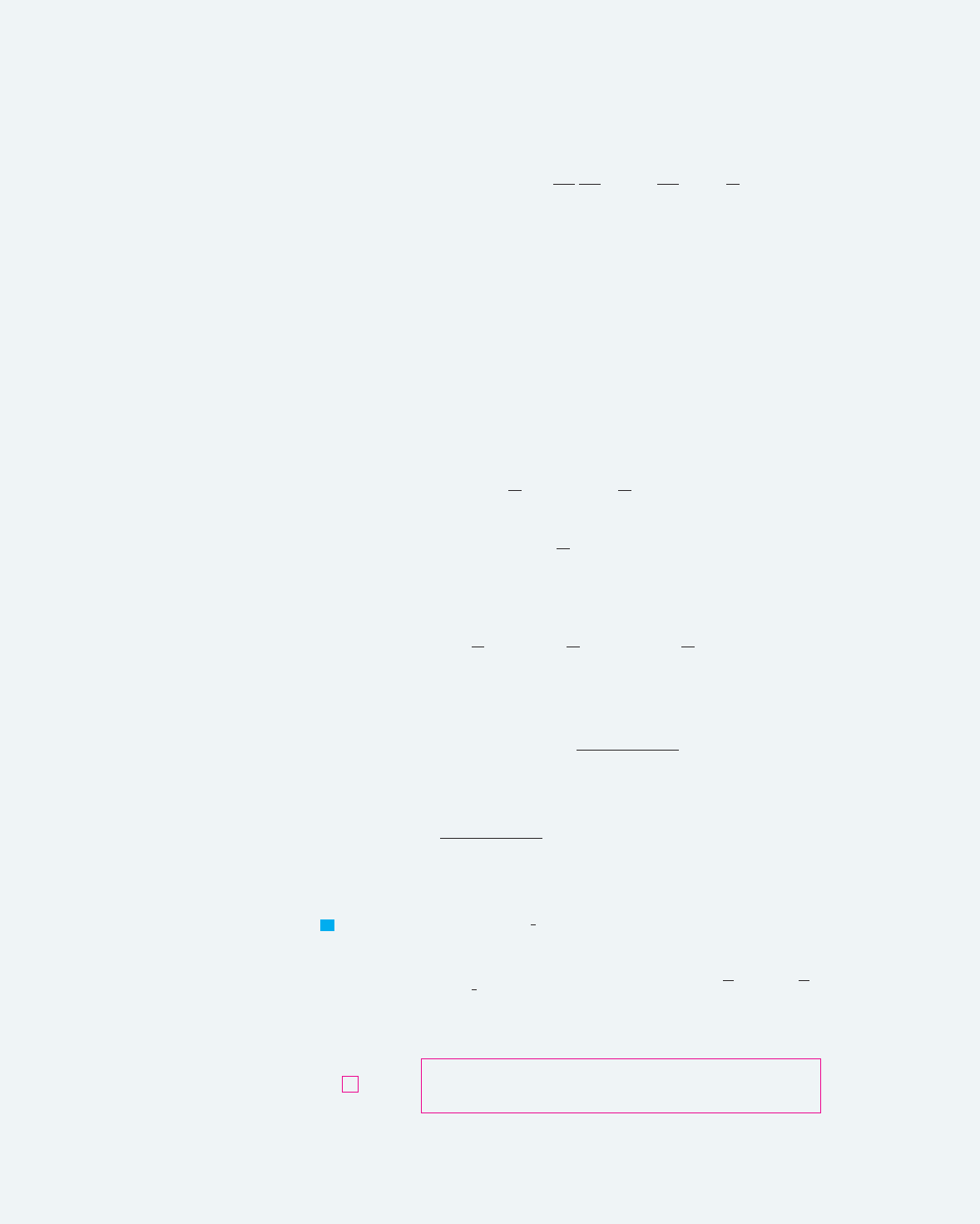
which shows that is increasing and concave downward on . Putting this informa-
tion together with (4), we draw the graph of in Figure 4.
Since and is an increasing continuous function that takes on arbitrarily
large values, the Intermediate Value Theorem shows that there is a number where takes
on the value 1. (See Figure 5.) This important number is denoted by .
DEFINITION is the number such that .
EXAMPLE 4 Use a graphing calculator or computer to estimate the value of .
SOLUTION According to Definition 5, we estimate the value of by graphing the curves
and and determining the -coordinate of the point of intersection. By
zooming in repeatedly, as in Figure 6, we find that
M
With more sophisticated methods, it can be shown that the approximate value of , to 20
decimal places, is
The decimal expansion of is nonrepeating because is an irrational number.
Now let’s use Formula 2 to differentiate functions that involve the natural logarithmic
function.
EXAMPLE 5 Differentiate .
SOLUTION To use the Chain Rule, we let . Then , so
M
In general, if we combine Formula 2 with the Chain Rule as in Example 5, we get
or
d
dx
!ln t"x#$ !
t!"x#
t"x#
d
dx
"ln u# !
1
u
du
dx
6
dy
dx
!
dy
du
du
dx
!
1
u
du
dx
!
1
x
3
" 1
"3x
2
# !
3x
2
x
3
" 1
y ! ln uu ! x
3
" 1
y ! ln"x
3
" 1#
V
ee
e % 2.71828182845904523536
e
e % 2.718
xy ! 1y ! ln x
e
e
ln e ! 1e
5
e
ln x
ln xln 1 ! 0
y ! ln x
"0, ##ln x
d
2
y
dx
2
! $
1
x
2
%
0
dy
dx
!
1
x
& 0
y ! ln x, x & 0
lim
x
l
0
"
ln x ! lim
t
l
#
ln
&
1
t
'
! lim
t
l
#
"$ln t# ! $#
x l 0
"
t l #t ! 1(x
x l #ln x l #1(x
ln xn l #ln"2
n
# l #ln 2 & 0ln"2
n
# ! n ln 2
r ! nx ! 2
424
|| ||
CHAPTER 7 INVERSE FUNCTIONS
F I G U R E 4
0
y
x
1
y=lnx
F I G U R E 5
0
y
1
x
1
e
y=lnx
y=1
y=lnx
0.98
2.752.7
1.02
F I G U R E 6
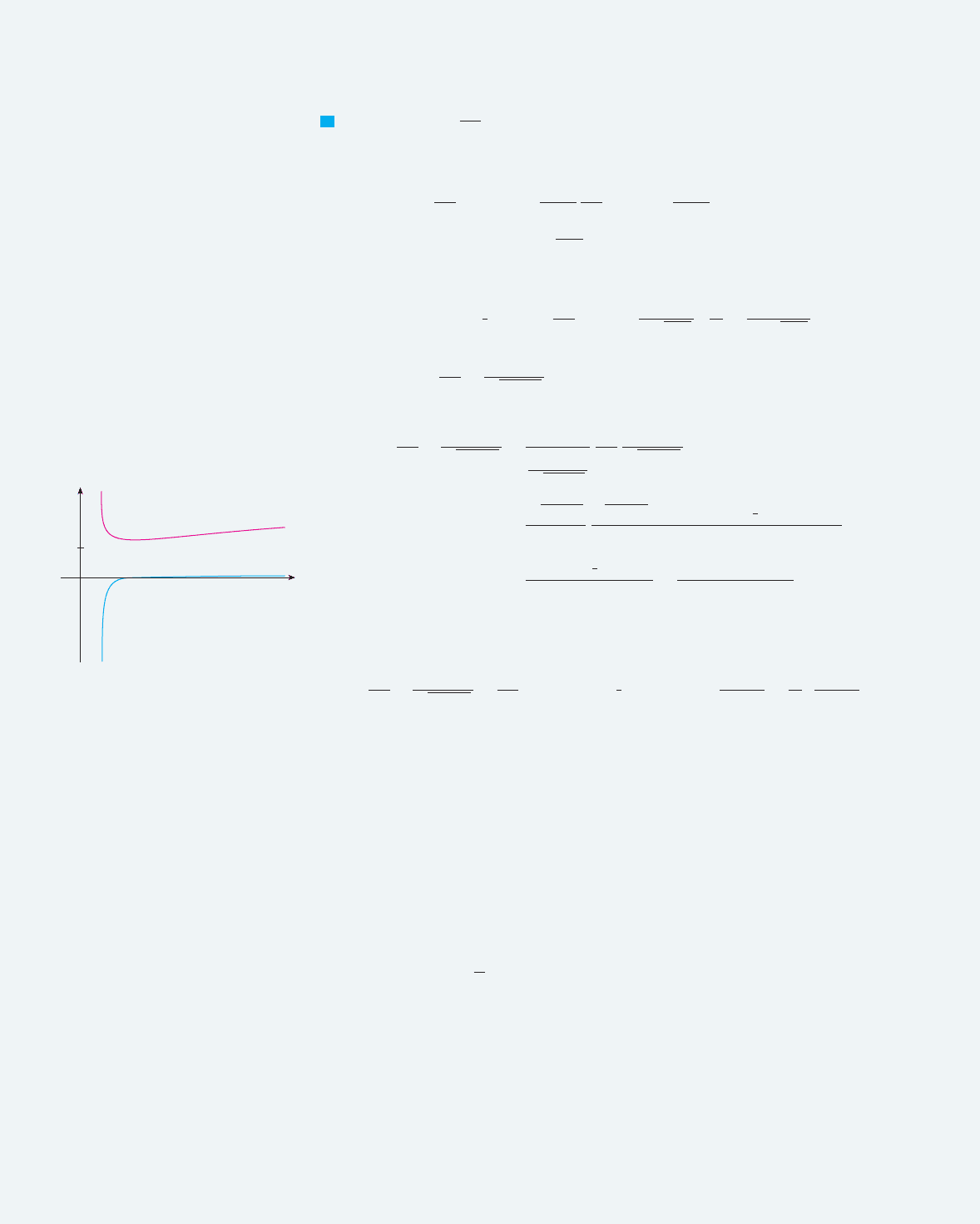
EXAMPLE 6 Find .
SOLUTION Using (6), we have
M
EXAMPLE 7 Differentiate .
SOLUTION This time the logarithm is the inner function, so the Chain Rule gives
M
EXAMPLE 8 Find .
SOLUTION 1
SOLUTION 2
If we first simplify the given function using the laws of logarithms, then the
differentiation becomes easier:
(This answer can be left as written, but if we used a common denominator we would see
that it gives the same answer as in Solution 1.) M
EXAMPLE 9 Discuss the curve using the guidelines of Section 4.5.
SOLUTION
A. The domain is
B. The -intercept is . To find the -intercept we set
We know that , so we have and therefore the
-intercepts are .
C. Since , is even and the curve is symmetric about the -axis.
D. We look for vertical asymptotes at the endpoints of the domain. Since
as and also as , we have
and
by (4). Thus the lines and are vertical asymptotes.x ! $2x ! 2
lim
x
l
$2
"
ln"4 $ x
2
# ! $#lim
x
l
2
$
ln"4 $ x
2
# ! $#
x l $2
"
x l 2
$
4 $ x
2
l 0
"
yff "$x# ! f "x#
'
s
3
x
4 $ x
2
! 1 ? x
2
! 3ln 1 ! 0
y ! ln"4 $ x
2
# ! 0
xf "0# ! ln 4y
)x
*
4 $ x
2
& 0+ ! )x
*
x
2
%
4+ ! )x
*
*
x
*
%
2+ ! "$2, 2#
y ! ln"4 $ x
2
#
!
1
x " 1
$
1
2
&
1
x $ 2
'
d
dx
ln
x " 1
s
x $ 2
!
d
dx
[
ln"x " 1# $
1
2
ln"x $ 2#
]
!
x $ 2 $
1
2
"x " 1#
"x " 1#"x $ 2#
!
x $ 5
2"x " 1#"x $ 2#
!
s
x $ 2
x " 1
s
x $ 2
( 1 $ "x " 1#
(
1
2
)
"x $ 2#
$1(2
x $ 2
d
dx
ln
x " 1
s
x $ 2
!
1
x " 1
s
x $ 2
d
dx
x " 1
s
x $ 2
d
dx
ln
x " 1
s
x $ 2
f !"x# !
1
2
"ln x#
$1(2
d
dx
"ln x# !
1
2
s
ln x
!
1
x
!
1
2x
s
ln x
f "x# !
s
ln x
d
dx
ln"sin x# !
1
sin x
d
dx
"sin x# !
1
sin x
cos x ! cot x
d
dx
ln"sin x#
V
SECTION 7.2* THE NATURAL LOGARITHMIC FUNCTION
|| ||
425
N Figure 7 shows the graph of the function
of Example 8 together with the graph of its deriv-
ative. It gives a visual check on our calculation.
Notice that is large negative when is
rapidly decreasing and when has
a minimum.
ff!"x# ! 0
ff !"x#
f
x
0
y
1
f
fª
F I G U R E 7
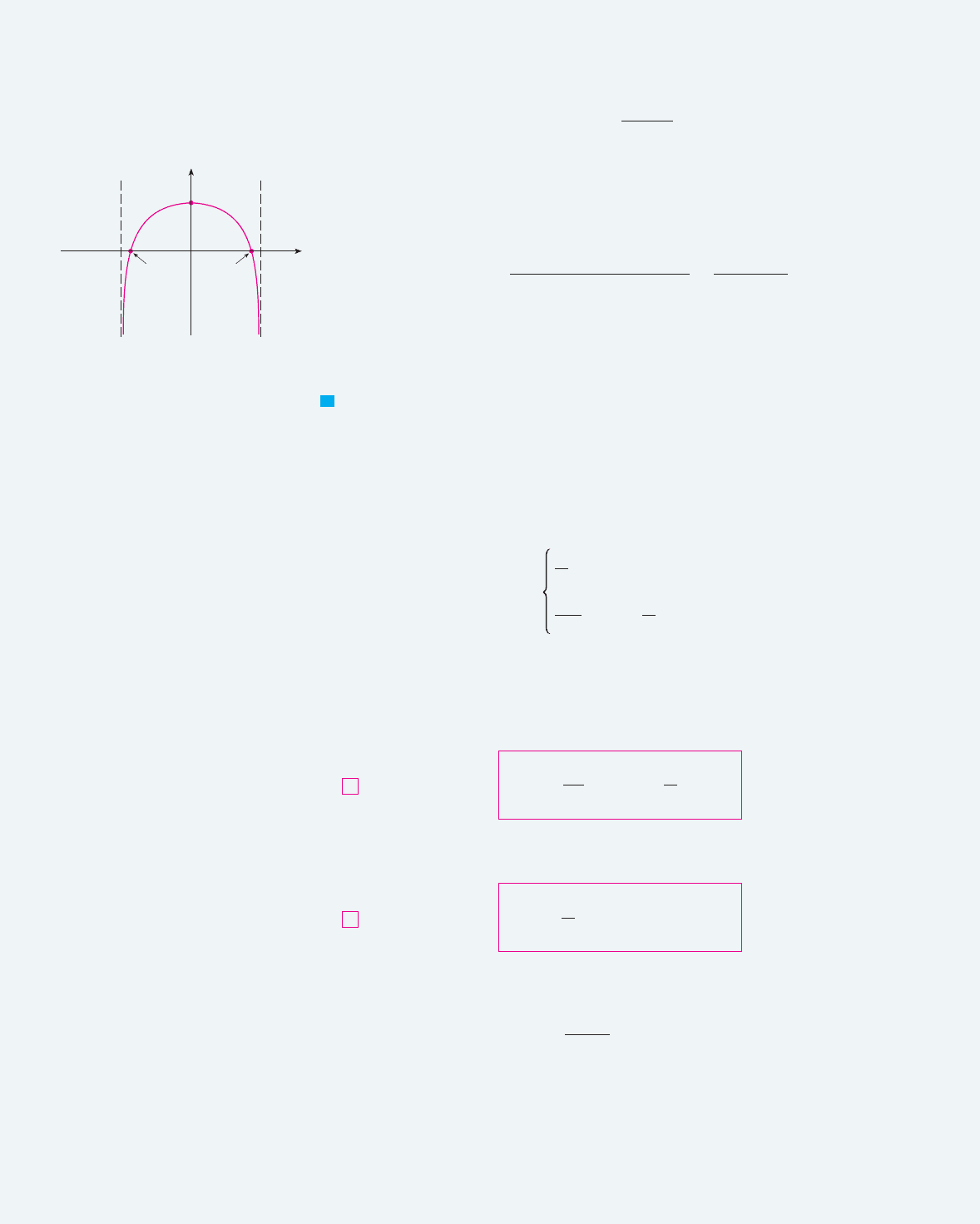
E.
Since when and when , is increasing
on and decreasing on .
F. The only critical number is . Since changes from positive to negative at ,
is a local maximum by the First Derivative Test.
G.
Since for all , the curve is concave downward on and has no
inflection point.
H. Using this information, we sketch the curve in Figure 8. M
EXAMPLE 10 Find if .
SOLUTION Since
it follows that
Thus for all . M
The result of Example 10 is worth remembering:
The corresponding integration formula is
Notice that this fills the gap in the rule for integrating power functions:
The missing case is supplied by Formula 8."n ! $1#
if n " $1
y
x
n
dx !
x
n"1
n " 1
" C
y
1
x
dx ! ln
*
x
*
" C
8
d
dx
(
ln
*
x
*
)
!
1
x
7
x " 0f !"x# ! 1(x
1
x
if x & 0
1
$x
"$1# !
1
x
if x
%
0
f !"x# !
f "x# !
,
ln x
ln"$x#
if x & 0
if x
%
0
f "x# ! ln
*
x
*
f !"x#
V
"$2, 2#x
f )"x#
%
0
f )"x# !
"4 $ x
2
#"$2# " 2x"$2x#
"4 $ x
2
#
2
!
$8 $ 2x
2
"4 $ x
2
#
2
f "0# ! ln 4
0f !x ! 0
"0, 2#"$2, 0#
f
0
%
x
%
2f !"x#
%
0$2
%
x
%
0
f !"x# & 0
f !"x# !
$2x
4 $ x
2
426
|| ||
CHAPTER 7 INVERSE FUNCTIONS
{œ„3,0}
{_œ„3,0}
0
y
x
x=2x=_2
(0,ln4)
F I G U R E 8
y=ln(4 -≈)
EXAMPLE 11 Evaluate .
SOLUTION We make the substitution because the differential occurs
(except for the constant factor 2). Thus and
Notice that we removed the absolute value signs because for all . We could
use the properties of logarithms to write the answer as
but this isn’t necessary. M
EXAMPLE 12 Calculate .
SOLUTION We let because its differential occurs in the integral. When
, ; when , . Thus
M
EXAMPLE 13 Calculate .
SOLUTION First we write tangent in terms of sine and cosine:
This suggests that we should substitute since then and so
:
M
Since , the result of Example 13 can also be
written as
y
tan x dx ! ln
*
sec x
*
" C
9
$ln
*
cos x
*
! ln"1(
*
cos x
*
# ! ln
*
sec x
*
! $ln
*
u
*
" C ! $ln
*
cos x
*
" C
y
tan x dx !
y
sin x
cos x
dx ! $
y
du
u
sin x dx ! $du
du ! $sin x dxu ! cos x
y
tan x dx !
y
sin x
cos x
dx
y
tan x dx
V
y
e
1
ln x
x
dx !
y
1
0
u du !
u
2
2
-
0
1
!
1
2
u ! ln e ! 1x ! eu ! ln 1 ! 0x ! 1
du ! dx(xu ! ln x
y
e
1
ln x
x
dx
V
ln
s
x
2
" 1 " C
xx
2
" 1 & 0
!
1
2
ln
*
x
2
" 1
*
" C !
1
2
ln"x
2
" 1# " C
y
x
x
2
" 1
dx !
1
2
y
du
u
!
1
2
ln
*
u
*
" C
x dx !
1
2
du
du ! 2x dxu ! x
2
" 1
y
x
x
2
" 1
dx
V
SECTION 7.2* THE NATURAL LOGARITHMIC FUNCTION
|| ||
427
x
0
y
0.5
1
e
y=
lnx
x
F I G U R E 9
N Since the function in
Example 12 is positive for , the integral
represents the area of the shaded region in
Figure 9.
x & 1
f "x# ! "ln x#(x

LOGARITHMIC DIFFERENTIATION
The calculation of derivatives of complicated functions involving products, quotients, or
powers can often be simplified by taking logarithms. The method used in the following
example is called logarithmic differentiation.
EXAMPLE 14 Differentiate .
SOLUTION We take logarithms of both sides of the equation and use the Laws of Loga-
rithms to simplify:
Differentiating implicitly with respect to gives
Solving for , we get
Because we have an explicit expression for , we can substitute and write
M
STEPS IN LOGARITHMIC DIFFERENTIATION
1.
Take natural logarithms of both sides of an equation and use the Laws
of Logarithms to simplify.
2. Differentiate implicitly with respect to .
3. Solve the resulting equation for .
If for some values of , then is not defined, but we can write
and use Equation 7.
*
y
*
!
*
f "x#
*
ln f "x#xf "x#
%
0
y!
x
y ! f "x#
dy
dx
!
x
3(4
s
x
2
" 1
"3x " 2#
5
&
3
4x
"
x
x
2
" 1
$
15
3x " 2
'
y
dy
dx
! y
&
3
4x
"
x
x
2
" 1
$
15
3x " 2
'
dy(dx
1
y
dy
dx
!
3
4
!
1
x
"
1
2
!
2x
x
2
" 1
$ 5 !
3
3x " 2
x
ln y !
3
4
ln x "
1
2
ln"x
2
" 1# $ 5 ln"3x " 2#
y !
x
3(4
s
x
2
" 1
"3x " 2#
5
V
428
|| ||
CHAPTER 7 INVERSE FUNCTIONS
N If we hadn’t used logarithmic differentiation in
Example 14, we would have had to use both the
Quotient Rule and the Product Rule. The resulting
calculation would have been horrendous.
7.
8.
9–12 Make a rough sketch of the graph of each function. Do not
use a calculator. Just use the graph given in Figure 4 and, if neces-
sary, the transformations of Section 1.3.
9. 10.
11. 12.
y ! 1 " ln"x $ 2#y ! ln"x " 3#
y ! ln
*
x
*
y ! $ln x
ln"a " b# " ln"a $ b# $ 2 ln c
ln"1 " x
2
# "
1
2
ln x $ ln sin x
1– 4 Use the Laws of Logarithms to expand the quantity.
1. 2.
3. 4.
5– 8 Express the quantity as a single logarithm.
5. 6. ln 3 "
1
3
ln 8ln 5 " 5 ln 3
ln
3x
2
"x " 1#
5
ln"uv#
10
ln
s
a"b
2
" c
2
#
ln
r
2
3
s
s
E X E R CI SE S
7.2*
49. Find a formula for if .
50. Find .
;
51–52 Use a graph to estimate the roots of the equation correct
to one decimal place. Then use these estimates as the initial
approximations in Newton’s method to find the roots correct to
six decimal places.
51. 52.
53–56 Discuss the curve under the guidelines of Section 4.5.
53. 54.
55. 56.
57. If , use the graphs of , , and to
estimate the intervals of increase and the inflection points of
on the interval .
;
58. Investigate the family of curves . What
happens to the inflection points and asymptotes as changes?
Graph several members of the family to illustrate what you
discover.
59–62 Use logarithmic differentiation to find the derivative of the
function.
59. 60.
61. 62.
63–72 Evaluate the integral.
63. 64.
65. 66.
67.
70.
71. 72.
73. Show that by (a) differentiating
the right side of the equation and (b) using the method of
Example 13.
74. Find, correct to three decimal places, the area of the region
above the hyperbola , below the -axis, and
between the lines and .
x ! $1x ! $4
xy ! 2("x $ 2#
x cot x dx ! ln
*
sin x
*
" C
y
sin"ln x#
x
dx
y
sin 2x
1 " cos
2
x
dx
y
cos x
2 " sin x
dx
y
"ln x#
2
x
dx
69.
y
6
e
dx
x ln x
68.
y
e
1
x
2
" x " 1
x
dx
y
9
4
&
s
x
"
1
s
x
'
2
dx
y
2
1
dt
8 $ 3t
y
2
1
4 " u
2
u
3
du
y
4
2
3
x
dx
y !
.
4
x
2
" 1
x
2
$ 1
y !
sin
2
x tan
4
x
"x
2
" 1#
2
y !
"x
3
" 1#
4
sin
2
x
s
3
x
y ! "2x " 1#
5
"x
4
$ 3#
6
c
f "x# ! ln"x
2
" c#
"0, 15$f
f )f !ff "x# ! ln"2x " x sin x#
CAS
y ! ln"x
2
$ 3x " 2#y ! ln"1 " x
2
#
y ! ln"tan
2
x#y ! ln"sin x#
ln"4 $ x
2
# ! x"x $ 4#
2
! ln x
d
9
dx
9
"x
8
ln x#
f "x# ! ln"x $ 1#f
"n#
"x#
13–14 Find the limit.
13.
14.
15–34 Differentiate the function.
15. 16.
17. 18.
19. 20.
21. 22.
24.
25. 26.
27.
29. 30.
31. 32.
33. 34.
35 –36 Find and .
35. 36.
37– 40 Differentiate and find the domain of .
38.
39. 40.
41. If , find .
42. If , find .
;
43– 44 Find . Check that your answer is reasonable by com-
paring the graphs of and .
43. 44.
45– 46 Find an equation of the tangent line to the curve at the
given point.
,
46.
47. Find if .
48. Find if .
ln xy ! y sin xy!
y ! ln"x
2
" y
2
#y!
y ! ln"x
3
$ 7#, "2, 0#"1, 0#y ! sin"2 ln x#
45.
f "x# ! ln"x
2
" x " 1#f "x# ! sin x " ln x
f !f
f !"x#
f )"e#f "x# !
ln x
x
f !"1#f "x# !
ln x
1 " x
2
f "x# ! ln ln ln xf "x# !
s
1 $ ln x
f "x# ! ln"x
2
$ 2x#f "x# !
x
1 $ ln"x $ 1#
37.
ff
y ! ln"sec x " tan x#y ! x
2
ln"2x#
y)y!
y ! ln
*
cos"ln x#
*
y ! tan!ln"ax " b#$
y ! ln tan
2
xy ! ln
*
2 $ x $ 5x
2
*
y ! "ln tan x#
2
f "u# !
ln u
1 " ln"2u#
y ! ln"x
4
sin
2
x#
28.
t"x# ! ln
(
x
s
x
2
$ 1
)
H"z# ! ln
.
a
2
$ z
2
a
2
" z
2
F"t# ! ln
"2t " 1#
3
"3t $ 1#
4
f "t# !
1 " ln t
1 $ ln t
t"x# ! ln
a $ x
a " x
23.
h"x# ! ln
(
x "
s
x
2
$ 1
)
f "x# ! sin x ln"5x#
f "x# ! ln
s
5
x
f "x# !
s
5
ln x
f "x# ! ln"sin
2
x#f "x# ! sin"ln x#
f "x# ! ln"x
2
" 10#f "x# !
s
x
ln x
lim
x l #
!ln"2 " x# $ ln"1 " x#$
lim
x
l
3
"
ln"x
2
$ 9#
SECTION 7.2* THE NATURAL LOGARITHMIC FUNCTION
|| ||
429

82. Refer to Example 1.
(a) Find an equation of the tangent line to the curve
that is parallel to the secant line .
(b) Use part (a) to show that .
83. By comparing areas, show that
84. Prove the third law of logarithms. [Hint: Start by showing
that both sides of the equation have the same derivative.]
85. For what values of do the line and the curve
enclose a region? Find the area of the region.
;
86. (a) Compare the rates of growth of and
by graphing both and in several viewing
rectangles. When does the graph of finally surpass the
graph of ?
(b) Graph the function in a viewing rect-
angle that displays the behavior of the function as .
(c) Find a number such that
then
Use the definition of derivative to prove that
lim
x
l
0
ln"1 " x#
x
! 1
87.
ln x
x
0.1
%
0.1x & Nif
N
x l #
h"x# ! "ln x#(x
0.1
t
f
tft"x# ! ln x
f "x# ! x
0.1
y ! x("x
2
" 1#
y ! mxm
1
2
"
1
3
" ( ( ( "
1
n
%
ln n
%
1 "
1
2
"
1
3
" ( ( ( "
1
n $ 1
ln 2 & 0.66
AD
y ! 1(t
75. Find the volume of the solid obtained by rotating the region
under the curve from 0 to 1 about the -axis.
76. Find the volume of the solid obtained by rotating the region
under the curve
from 0 to 3 about the -axis.
77. The work done by a gas when it expands from volume
to volume is , where is the
pressure as a function of the volume . (See Exercise 27 in
Section 6.4.) Boyle’s Law states that when a quantity of gas
expands at constant temperature, , where is a con-
stant. If the initial volume is 600 and the initial pressure
is 150 kPa, find the work done by the gas when it expands at
constant temperature to 1000 .
78. Find if , , , and .
79. If is the inverse function of , find .
;
80. (a) Find the linear approximation to near l.
(b) Illustrate part (a) by graphing and its linearization.
(c) For what values of is the linear approximation accurate
to within 0.1?
81. (a) By comparing areas, show that
(b) Use the Midpoint Rule with to estimate .
ln 1.5n ! 10
1
3
%
ln 1.5
%
5
12
x
f
f "x# ! ln x
t!"2#f "x# ! 2x " ln xt
f "2# ! 0f "1# ! 0x & 0f )"x# ! x
$2
f
cm
3
cm
3
CPV ! C
V
P ! P"V #W !
x
V
2
V
1
P dVV
2
V
1
y
y !
1
x
2
" 1
xy ! 1(
s
x " 1
430
|| ||
CHAPTER 7 INVERSE FUNCTIONS
THE NATURAL EXPONENTIAL FUNCTION
Since ln is an increasing function, it is one-to-one and therefore has an inverse function,
which we denote by exp. Thus, according to the definition of an inverse function,
and the cancellation equations are
In particular, we have
We obtain the graph of by reflecting the graph of about the line
y ! ln xy ! exp x
exp"1# ! e since ln e ! 1
exp"0# ! 1 since ln 1 ! 0
exp"ln x# ! x and ln"exp x# ! x
2
exp"x# ! y &? ln y ! x
1
7.3*
f
$1
"x# ! y &? f " y# ! x
f " f
$1
"x## ! x
f
$1
" f "x## ! x

(See Figure 1.) The domain of is the range of ln, that is, ; the range of
exp is the domain of ln, that is, .
If is any rational number, then the third law of logarithms gives
Therefore, by (1),
Thus whenever is a rational number. This leads us to define , even for irra-
tional values of , by the equation
In other words, for the reasons given, we define to be the inverse of the function . In
this notation (1) becomes
and the cancellation equations (2) become
EXAMPLE 1 Find if .
SOLUTION 1 From (3) we see that
Therefore .
SOLUTION 2 Start with the equation
and apply the exponential function to both sides of the equation:
But (4) says that . Therefore . M
EXAMPLE 2 Solve the equation .
SOLUTION We take natural logarithms of both sides of the equation and use (5):
x !
1
3
"5 $ ln 10#
3x ! 5 $ ln 10
5 $ 3x ! ln 10
ln"e
5$3x
# ! ln 10
e
5$3x
! 10
V
x ! e
5
e
ln x
! x
e
ln x
! e
5
ln x ! 5
x ! e
5
e
5
! xmeansln x ! 5
ln x ! 5x
ln"e
x
# ! x for all x
5
e
ln x
! x x & 0
4
e
x
! y &? ln y ! x
3
ln xe
x
e
x
! exp"x#
x
e
x
xexp"x# ! e
x
exp"r# ! e
r
ln"e
r
# ! r ln e ! r
r
"0, ##
"$#, ##expy ! x.
SECTION 7.3* THE NATURAL EXPONENTIAL FUNCTION
|| ||
431
F I G U R E 1
y
1
0
x
y=x
y=lnx
y=expx
1
