Trauth M.H., MATLAB® Recipes for Earth Sciences, Third edition

Подождите немного. Документ загружается.

128 5 TIME-SERIES ANALYSIS

Original data point

Linearly-interpolated

data series

Spline-interpolated

data series

350 360 370 380 390 400 410 420 430 440 450

−25

−20

−15

−10

−5

x(t)

Interpolated Signals

Fig. 5.9 Interpolation artifacts. Whereas the linearly interpolated points are always within

the range of the original data, the spline interpolation method causes unrealistic high and

low values.

series1S = interp1(series1(:,1),series1(:,2),t,'spline');

series2L = interp1(series2(:,1),series2(:,2),t,'linear');

series2S = interp1(series2(:,1),series2(:,2),t,'spline');

 e results are compared by plotting the  rst series before and a er inter-

polation.

plot(series1(:,1),series1(:,2),'ko'), hold on

plot(t,series1L,'b-',t,series1S,'r-'), hold off

We can already observe some signi cant artifacts at ca. 370 kyrs. Whereas

the linearly-interpolated points are always within the range of the original

data, the spline interpolation method produces values that are unrealisti-

cally high or low (Fig. 5.9).  e results can be compared by plotting the sec-

ond data series.

plot(series2(:,1),series2(:,2),'ko'), hold on

plot(t,series2L,'b-',t,series2S,'r-'), hold off

In this series, only a few artifacts can be observed. We can apply the func-

tion used above to calculate the power spectrum computing the FFT for

256 data points, with a sampling frequency of 1/3 kyrs

–1

[Pxx,f] = periodogram(series1L,[],256,1/3);

plot(f,Pxx)

xlabel('Frequency')

5.5 INTERPOLATING AND ANALYZING UNEVENLY-SPACED DATA 129

5 TIME-SERIES ANALYSIS

ylabel('Power')

title('Auto-Spectrum')

Signi cant peaks occur at frequencies of approximately 0.01, 0.025 and 0.05,

corresponding approximately to the 100, 40 and 20 kyr cycles. Analysis of

the second time series

[Pxx,f] = periodogram(series2L,[],256,1/3);

plot(f,Pxx)

xlabel('Frequency')

ylabel('Power')

title('Auto-Spectrum')

also yields signi cant peaks at frequencies of 0.01, 0.025 and 0.05 (Fig. 5.10).

Now we compute the cross-spectrum for both data series.

[Pxy,f] = cpsd(series1L,series2L,[],128,256,1/3);

plot(f,abs(Pxy))

xlabel('Frequency')

ylabel('Power')

title('Cross-Spectrum')

 e correlation, as indicated by the high value for the coherence, is quite

convincing.

[Cxy,f] = mscohere(series1L,series2L,[],128,256,1/3);

plot(f,Cxy)

xlabel('Frequency')

ylabel('Magnitude Squared Coherence')

title('Coherence')

We can observe a fairly high coherence at frequencies of 0.01, 0.025 and 0.05.

 e complex part of

Pxy is required for calculating the phase di erence for

each frequency.

phase = angle(Pxy);

plot(f,phase)

xlabel('Frequency')

ylabel('Phase Angle')

title('Phase spectrum')

 e phase shi at a frequency of f=0.01 is calculated by

interp1(f,phase,0.01)

which produces the output of

130 5 TIME-SERIES ANALYSIS

t Frequency

1st data series

2nd data

series

=0.01

=0.025

=0.05

High coherence in

the 0.01 frequency

band

Phase angle in the 0.01

frequency band

0.4

0.6

0.8

0 0.05 0.15

0.1

0.2

−4

−3

−2

−1

100

200

300

400

500

600

700

−5

0 200 400 600 800 1000

0 0.05 0.1 0.15 0.2

x(t)

Power

Coherence

Phase angle

Frequency

Phase Spectrum

Time Domain

Cross-Spectrum

Coherence

Fig. 5.10 Result from cross-spectral analysis of the two linearly-interpolated signals:

a signals in the time domain, b cross-spectrum of both signals, c coherence of the signals in

the frequency domain and d phase spectrum in radians.

ans =

-0.2796

 e phase spectrum is normalized to a full period τ=2π, and therefore the

phase shi of –0.2796 equals (–0.2796*100 kyrs)/(2*π)=–4.45 kyrs.  is

corresponds roughly to the phase shi of 5 kyrs introduced to the second

data series with respect to the  rst series.

As a more convenient tool for spectral analysis, the Signal Processing

Toolbox also contains a GUI function named

sptool, which stands for

Signal Processing Tool.

5.6 EVOLUTIONARY POWER SPECTRUM 131

5 TIME-SERIES ANALYSIS

5.6 Evolutionary Power Spectrum

 e amplitude of spectral peaks usually varies with time.  is is particularly

true for paleoclimate time series. Paleoclimate records usually show trends

in the mean and variance, but also in the relative contributions of rhythmic

components such as the Milankovitch cycles in marine oxygen-isotope re-

cords. Evolutionary powerspectra have the ability to map such changes in

the frequency domain.  e evolutionary or windowed power spectrum is a

modi cation of the method introduced in Section 5.3, which computes the

spectrum of overlapping segments of the time series.  ese overlapping seg-

ments are relatively short compared to the windowed segments used by the

Welch method (Section 5.3), which is used to increase the signal-to-noise

ratio of powerspectra.  e evolutionary power spectrum method therefore

uses the Short-Time Fourier Transform (STFT) instead of the Fast Fourier

Transformation (FFT).  e output of evolutionary power spectrum is the

short-term, time-localized frequency content of the signal.  ere are vari-

ous methods to display the results. For instance, time and frequency can be

plotted on the x- and y-axes, respectively, or vice versa, with the color of the

plot being dependent on the height of the spectral peaks.

As an example, we generate a data set that is similar to those used in

Section 5.5.  e data series contains three main periodicities of 100, 40 and 20

kyrs and additive Gaussian noise.  e amplitudes, however, change through

time and this example can therefore be used to illustrate the advantage of the

evolutionary power spectrum method. We  rst create a time vector

clear

t = 0 : 3 : 1000;

We then introduce some Gaussian noise to the time vector t to make the

data unevenly spaced.

randn('seed',0);

t = t + randn(size(t));

Next, we compute the signal with the three periodicities and varying am-

plitudes.  e 40 kyr cycle appears a er ca. 450 kyrs, whereas the 100 and 20

kyr cycles are present throughout the time series.

x1 = 0.5*sin(2*pi*t/100) + ...

1.0*sin(2*pi*t/40) + ...

0.5*sin(2*pi*t/20);

x2 = 0.5*sin(2*pi*t/100) + ...

0.5*sin(2*pi*t/20);

132 5 TIME-SERIES ANALYSIS

x = x1; x(1,150:end) = x2(1,150:end);

We then add Gaussian noise to the signal.

x = x + 0.5*randn(size(x));

Finally, we save the synthetic data series to the  le series3.txt on the hard

disk and clear the workspace.

series3(:,1) = t;

series3(:,2) = x;

series3(1,1) = 0;

series3(end,1) = 1000;

series3 = sortrows(series3,1);

save series3.txt series3 -ascii

 e above series of commands illustrates how to generate synthetic time

series that show the same characteristics as oxygen-isotope data from cal-

careous algae (foraminifera) in deep-sea sediments.  is synthetic data set

is suitable for use in demonstrating the application of methods for spectral

analysis.  e following sequence of commands assumes that real data are

contained in a  le named series3.txt. We  rst load and display the data

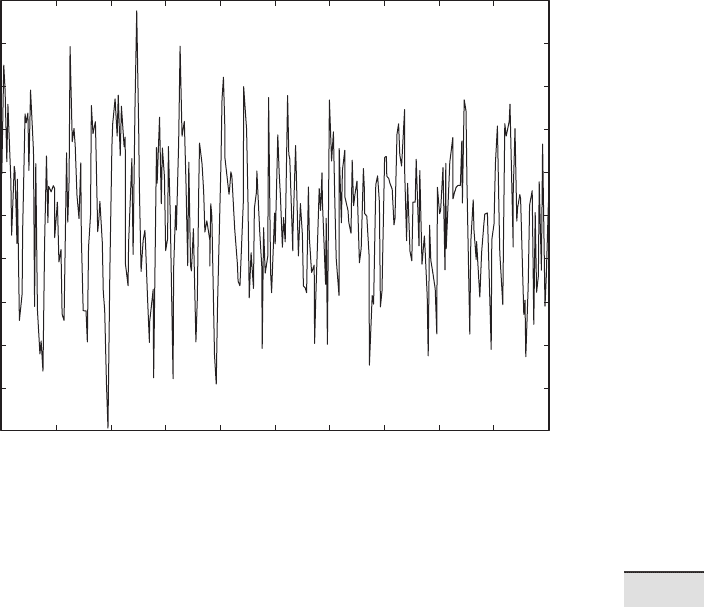
(Fig. 5.11).

clear

series3 = load('series3.txt');

plot(series3(:,1),series3(:,2))

xlabel('Time (kyr)')

ylabel('d18O (permille)')

title('Signal with Varying Cyclicities')

Since both, the standard and the evolutionary power spectrum methods re-

quire evenly-spaced data, we interpolate the data to an evenly-spaced time

vector

t as demonstrated in Section 5.5.

t = 0 : 3 : 1000;

series3L = interp1(series3(:,1),series3(:,2),t,'linear');

We then compute a non-evolutionary power spectrum for the full length of

the time series (Fig. 5.12).  is exercise helps us to compare the di erences

between the results of the standard and the evolutionary power spectrum

methods.

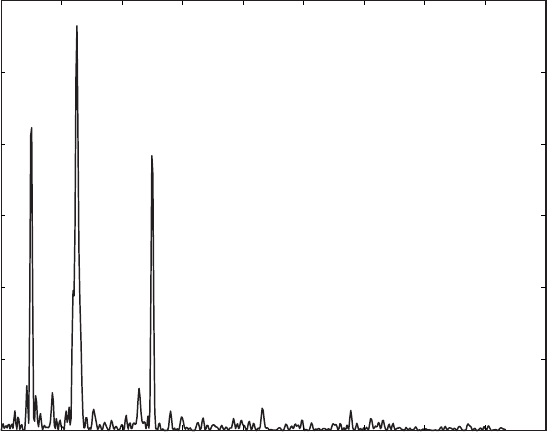
[Pxx,f] = periodogram(series3L,[],1024,1/3);

plot(f,Pxx)

xlabel('Frequency')

ylabel('Power')

title('Power Spectrum')

5.6 EVOLUTIONARY POWER SPECTRUM 133

5 TIME-SERIES ANALYSIS

0 100 200 300 400 500 600 700 800 900 1000

−2.5

−2.0

−1.5

−1.0

−0.5

0.0

0.5

1.0

1.5

2.0

2.5

d18O (permille)

Time (kyr)

Signal with Varying Cyclicities

Fig. 5.11 Synthetic data set containing three main periodicities of 100, 40, and 20 kyrs and

additive Gaussian noise. Whereas the 100 and 20 kyr cycles are present throughout the time

series, the 40 kyr cycle only appears at around 450 kyrs before present.

 e auto-spectrum shows signi cant peaks at 100, 40 and 20 kyr cyclicities,

as well as some noise.  e power spectrum, however, does not provide any

information about  uctuations in the amplitudes of these peaks.  e non-

evolutionary power spectrum simply represents an average of the spectral

information contained in the data.

We now use the function

spectrogram to map the changes in the

power spectrum with time. By default, the time series is divided into eight

segments with a 50 % overlap. Each segment is windowed with a Hamming

window to suppress spectral leakage (Section 5.3).  e function

spectro-

gram uses similar input parameters to those used in periodogram in

Section 5.3. We then compute the evolutionary power spectrum for a win-

dow of 64 data points with a 50 data point overlap.  e STFT is computed

for

nfft=256. Since the spacing of the interpolated time vector is 3 kyrs,

134 5 TIME-SERIES ANALYSIS

0.02

0.04

0.06

0.08

0.1

0.140.12 0.16 0.18

100

120

Power

Frequency

Power Spectrum

Fig. 5.12 Power spectrum for the full time series showing signi cant peaks at 100, 40 and

20 kyrs.  e plot, however, does not provide any information on the temporal behavior of

the cyclicities.

the sampling frequency is 1/3 kyr

–1

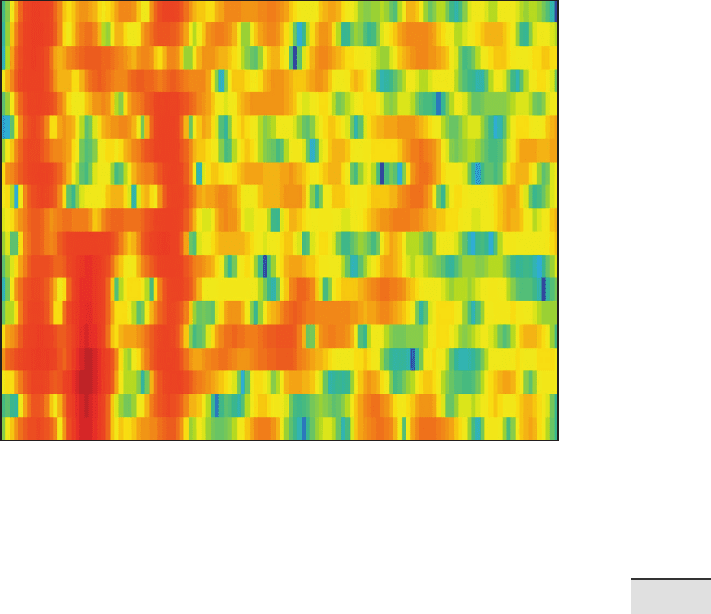
spectrogram(series3L,64,50,256,1/3)

title('Evolutionary Power Spectrum')

xlabel('Frequency (1/kyr)')

ylabel('Time (kyr)')

 e output of spectrogram is a color plot (Fig. 5.13) that displays vertical

stripes in red representing signi cant maxima at frequencies of 0.01 and

0.05 kyr

–1

, or 100 and 20 kyr cyclicities.  e 40 kyr cycle (corresponding

to a frequency of 0.025 kyr

–1

), however, only occurs a er ca. 450 kyrs, as

documented by the vertical red stripe in the lower half of the graph.

To improve the visibility of the signi cant cycles, the coloration of the

graph can be modi ed using the colormap editor.

colormapeditor

5.7 LOMB-SCARGLE POWER SPECTRUM 135

5 TIME-SERIES ANALYSIS

0 0.02 0.04 0.06 0.08 0.1 0.12 0.14 0.16

100

200

300

400

500

600

700

800

900

Frequency (1/kyr)

Time (kyr)

Evolutionary Power Spectrum

Fig. 5.13 Evolutionary power spectrum using spectrogram, which computes the short-

time Fourier transform STFT of overlapping segments of the time series. We use a Hamming

window of 64 data points and 50 data points overlap.  e STFT is computed for a nfft=256.

Since the spacing of the interpolated time vector is 3 kyrs the sampling frequency is 1/3 kyr

-1

 e plot shows the onset of the 40 kyr cycle at around 450 kyrs before present.

 e colormap editor displays the colormap of the  gure as a strip of rect-

angular cells.  e nodes that separate regions of uniform slope in the RGB

colormap can be shi ed by using the mouse, which introduces distortions

in the colormap and results in modi cation of the spectrogram colors. For

example, shi ing the yellow node towards the right increases the contrast

between vertical peak areas at 100, 40 and 20 kyrs, and the background.

5.7 Lomb-Scargle Power Spectrum

 e power spectrum methods introduced in the previous sections require

evenly-spaced data. In earth sciences, however, time series are o en un-

evenly spaced. Although interpolating the unevenly-spaced data to a grid of

136 5 TIME-SERIES ANALYSIS

evenly-spaced times is one way to overcome this problem (Section 5.5), in-

terpolation introduces numerous artifacts to the data, in both the time and

frequency domains. For this reason, an alternative method of time-series

analysis has become increasingly popular in earth sciences Lomb-Scargle

algorithm (e. g., Scargle 1981, 1982, 1989, 1990, Press et al. 1992, Schulz et al.

1998).

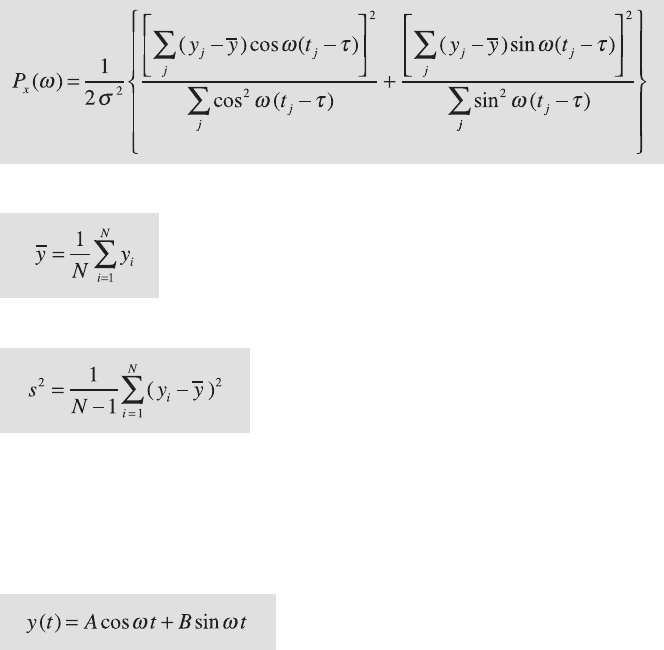
 e Lomb-Scargle algorithm evaluates the data of the time series only

at the times t

that are actually measured. Assuming a series y(t) of N data

points, the Lomb-Scargle normalized periodogram P

as a function of an-

gular frequency ω = 2πf > 0 is given by

where

and

are the arithmetic mean and the variance of the data (Section 3.2).  e con-

stant τ is an o set that makes P

(ω) independent of shi ing the t

’s by any

constant amount. Scargle (1982) showed that this particular choice of the

o set τ has the consequence that the solution for P

(ω) is identical to a

least-squares  t of sine and cosine functions to the data series y(t):

 e least-squares  t of harmonic functions to data series in conjunction

with spectral analysis had previously been investigated by Lomb (1976), and

hence the method is called the normalized Lomb-Scargle Fourier transform.

 e term normalized refers to the factor s

in the dominator of the equation

for the periodogram.

5.7 LOMB-SCARGLE POWER SPECTRUM 137

5 TIME-SERIES ANALYSIS

Scargle (1982) has shown that the Lomb-Scargle periodogram has an

exponential probability distribution with unit mean.  e probability that

(ω) will be between some positive quantity z and z+dz is exp(–z)dz. If

we scan M independent frequencies, the probability of none of them having

a larger value than z is (1–exp(–z))M. We can therefore compute the false-

alarm probability of the null hypothesis, e. g., the probability that a given

peak in the periodogram is not signi cant, by

Press et al. (1992) suggested using the Nyquist criterion (Section 5.2) to de-

termine the number of independent frequencies M assuming that the data

were evenly spaced. In this case, the appropriate value for the number of in-

dependent frequencies is M = 2N, where N is the length of the time series.

More detailed discussions of the Lomb-Scargle method are given in

Scargle (1989) and Press et al. (1992). An excellent summary of the method

and a TURBO PASCAL program to compute the normalized Lomb-Scargle

power spectrum of paleoclimatic data have been published by Schulz and

Stattegger (1998). A convenient MATLAB algorithm

lombscargle for com-

puting the Lomb-Scargle periodogram has been published by Brett Shoelson

( e MathWorks Inc.) and can be downloaded from File Exchange at

http://www.mathworks.com/matlabcentral/fileexchange/

 e following MATLAB code is based on the original FORTRAN code pub-

lished by Scargle (1989). Signi cance testing uses the methods proposed by

Press et al. (1992) explained above.

We  rst load the synthetic data that were generated to illustrate the use

of the evolutionary or windowed power spectrum method in Section 5.6.

 e data contain periodicities of 100, 40 and 20 kyrs, as well as additive

Gaussian noise, and are unevenly spaced about the time axis. We de ne two

new vectors

t and x that contain the original time vector and the synthetic

oxygen-isotope data sampled at times

clear

series3 = load('series3.txt');

t = series3(:,1);

x = series3(:,2);

We then generate a frequency axis f. Since the Lomb-Scargle method is not

able to deal with the zero-frequency portion, i. e., with in nite periods, we

start at a frequency value that is equivalent to the spacing of the frequency