Волькенштейн М.В. Общая биофизика

Подождите немного. Документ загружается.

9.5. ТЕРМОДИНАМИКА И ЭВОЛЮЦИЯ 501

Мы

видим, что уравнения

(9.32)

(9.33)

описывают эволюцию

системы в разных шкалах времени. Уравнения

(9.32)

(9.36)

представляют быструю продукцию нового вещества Y при прак-

тически постоянных значениях {л:}, уравнения (9.33)—медлен-

ное

изменение {х} после того, как у достигло своего стабильного

значения,

отвечающего

G({x},

у, 0) = 0. Тем самым селекция

должна происходить весьма быстро. С термодинамической точки

зрения

ситуация эквивалентна представленной на рис. 9.4 — из-

быточная продукция энтропии, созданная флуктуациями, т. е.

добавочная диссипация, становится отрицательной. Энтропия и

ее продукция являются стохастическими функциями флуктуи-

рующих переменных, и термодинамические величины получаются

путем усреднения этих функций. При появлении нового веще-

ства Y можно построить функцию состояния, связанную с вводи-

мой

таким образом диссипацией. Для устойчивой системы эта

функция

имеет минимум. Эволюция возникает, если функция

имеет более чем один экстремум или

седловую

точку. Это — ва-

риационный

принцип, характеризующий эволюцию. После точки

перехода продукция энтропии возрастает, так как система пере-

ключается на путь быстрого синтеза вещества Y.

В случае, характеризуемом ю

-ц ~ е (см. (9.31)), уравнения

(9.34)

(9.35)

описывают (при неустойчивости) медленную эво-

люцию вещества Y к новому режиму. Сравнение с уравнением

Эйгена

(9.14)

показывает, что фактор е можно интерпретиро-

вать как среднюю скорость мутаций, причем неустойчивость не-

посредственно определяется ошибками копирования. В

случае

(о„+1

~ е~' (см. (9.30)) роль мутаций состояла во введении свя-

зей

между

старыми и новыми переменными. Эволюция через

неустойчивость определялась появлением новых элементов, как,

например,

новых ферментов.

Положим

в уравнении

(9.34)

G\ = 0, т. е. допустим, что но-

вое вещество производится только мутациями. Исходная си-

стема

(9.29)

может стать неустойчивой, если

— возрастаю-

щая

функция у вблизи

({х

у, 0), где х

— решения- исходной

системы. В точке перехода добавочная диссипация, вводимая Y

соответствующими изменениями x

, становится отрицательной.

Наиболее интересно положение, относящееся к

случаю

(9.30),—

когда система, эволюционируя к новому устойчивому режиму,

увеличивает свою диссипацию. Такое поведение противоположно

поведению вблизи стационарного состояния, не сильно удален-

ного от равновесия и устойчивого по отношению к флуктуациям.

После

достижения нового режима система вновь стремится

уменьшить свою диссипацию.

Эти представления можно иллюстрировать простой кинети-

ческой моделью [53, 54]. Рассмотрим открытую систему, в кото-

рой

имеется поток мономеров

двух

видов (скажем, нуклеотидов)

502

ГЛ.

ПРОБЛЕМЫ РАЗВИТИЯ

и Ь.

Внутри системы,

«ящике», происходит полимеризация,

образуются цепи

Ai и В.

Реакция образования

протекает

через промежуточную форму

соответствующую объединению

мономеров

а в

линейный ансамбль, образованный нехимиче-

скими

взаимодействиями. Такой ансамбль может переходить

другое

состояние

R*.

Имеем реакции

Как

только образовались

Ai, R* и В,

включается автокаталити-

ческий цикл,

котором

действует

как

матрица

для

синтеза

из b и В

действует

как мат-

рица, превращающая

R* в At.

А] и В

диффундируют

из

«ящика»

или

дезактивируются.

Имеем

д диффузия

диффузия

7,5

ZM 2,5 3,0

Концентрация

мономеров

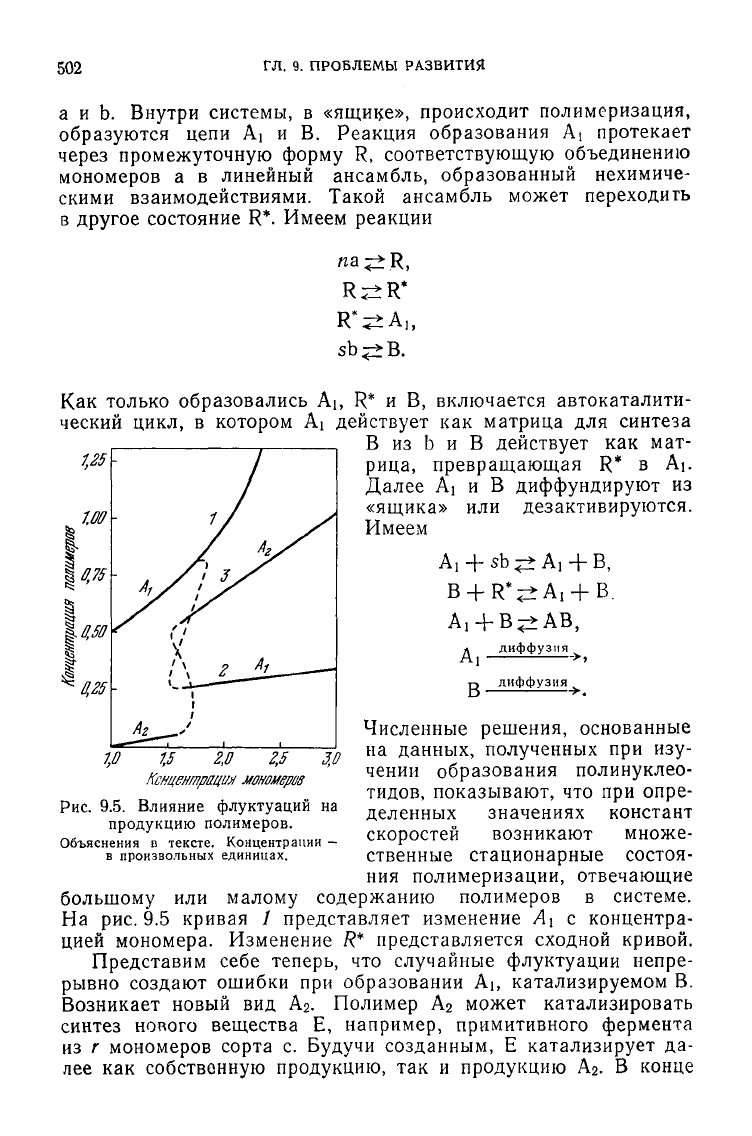
Рис.

9.5. Влияние флуктуации на

продукцию полимеров.

Объяснения

тексте. Концентрации

—

в произвольных единицах.

Численные решения, основанные

на

данных, полученных

при изу-

чении образования полинуклео-

тидов, показывают,

что при

опре-

деленных значениях констант

скоростей возникают множе-

ственные стационарные состоя-

ния

полимеризации, отвечающие

большому

или

малому содержанию полимеров

системе.

На

рис.

9.5

кривая

представляет изменение

А\ с

концентра-

цией

мономера. Изменение

представляется сходной кривой.

Представим себе теперь,

что

случайные флуктуации непре-

рывно создают ошибки

при

образовании

Аь

катализируемом

В.

Возникает новый

вид А

Полимер

может катализировать

синтез нового вещества

Е,

например, примитивного фермента

из

мономеров сорта

с.

Будучи созданным,

катализирует

да-

лее

как

собственную продукцию,

так и

продукцию

. В

конце

9.5. ТЕРМОДИНАМИКА И ЭВОЛЮЦИЯ 503

концов

Е и А

уходят

из «ящика». Имеем

B + R*§A

+B,

rc + A

j±E + A

B + R

+ E^B + A

+ E,

rc + A

+ E^2E + A

диффузия

Эта система реакций описывает нелинейное сопряжение

между

и Е, которое тем сильнее, чем больше R*. А] и R* зависят от

стационарного состояния, достигнутого при полимеризации. Ре-

зультаты численных расчетов показаны на рис. 9.5. При малой

концентрации

мономеров доминируют полимеры Аь Это стацио-

нарное

состояние могло бы продолжаться (кривая У), но флук-

туации создают новый полимер А

и катализатор, усиливающий

продукцию А

. При критическом значении концентрации моно-

меров возникают неустойчивости (пунктирные кривые), и си-

стема резко переключается в новое стационарное состояние,

котором доминируют полимеры А

(кривые 2 и 3). Переход

вызван как мутациями, так и появлением катализатора Е. Пер-

вые

служат

триггером неустойчивости, второй определяет ост-

роту перехода. В этом смысле модель объединяет случаи

(9.30)

(9.31). Описанное эволюционное поведение системы связано

с ее автокаталитическими, нелинейными свойствами.

Термодинамика

дает

общее понимание эволюции. В частно-

сти,

возрастание диссипации может привести к эволюционной

обратной связи, создающей путь к новой неустойчивости, к даль-

нейшей

эволюции системы. Наибольшая приспособленность при

этом не обязательно означает наибольшее размножение.

Конечно,

такой детерминистический анализ должен быть до-

полнен

и уточнен стохастическим (см. стр. 491).

Очевидно, что приведенное рассмотрение не

дает

еще теории

эволюции

в истинном значении этого слова. Однако оно раскры-

вает физический смысл эволюции и имеет безусловное иллюстра-

тивное значение.

Следует

отметить, что качественные соображения сходного

характера были высказаны ранее Молчановым [12], указавшим,

что статистическая термодинамика, как таковая, применима

лишь

к ранним стадиям эволюции. Смысл этого утверждения

состоит в том, что «применимость статистических представлений

уменьшается в процессе эволюции, так как уменьшается число

частиц» — скажем, из мономеров образуются полимеры. Теории

Эйгена и Пригожина имеют уже не термодинамический, но

504 ГЛ. 9.

ПРОБЛЕМЫ

РАЗВИТИЯ

кинетический

характер. Роль термодинамики сводится, в конеч-

ном

счете, к анализу неустойчивостей.

Изложенная

в §§

9.3—9.5

область теоретической физики на-

ходится на начальной стадии своего развития. Однако пути этого

развития намечены, и понимание добиологической эволюции вы-

шло за пределы качественных спекуляций.

§ 9.6. ТЕОРИЯ ПЕРЕХОДА К БИОЛОГИЧЕСКОЙ ЭВОЛЮЦИИ

В теории Эйгена селекция и эволюция реализуются в си-

стеме нуклеиново-белковых гиперциклов. Ответ на вопрос о том,

что было ранее — «законодательная» нуклеиновая кислота или

«исполнительный» белок — гласит: и то, и

другое.

Та же схема

фигурирует в только что приведенной кинетической модели.

Кун

предложил качественную модель происхождения жизни,

исходящую из того, что вторая стадия добиологической эволю-

ции

началась со сравнительно коротких цепей РНК [55]. Опи-

шем эту модель.

В «первичном

бульоне»

происходит синтез и распад нуклео-

тидов. Процессы эти

грубо

периодичны — за фазой образования

следует

фаза разложения. Чередование фаз определяется сменой

высыхания и увлажнения прибрежного раствора. Однако обра-

зовавшиеся нуклеотиды полимеризуются, причем в цепи с рав-

ной

вероятностью

входят

правая и левая рибоза. Случайное

возникновение

цепи, содержащей 20 D-рибозных звеньев, имеет

вероятность (1/2)

= 1(H.

Упорядоченные, т. е. содержащие лишь один стереоизомер,

короткие

цепи

могут

служить матрицами для саморепродукции

они более устойчивы к гидролизу. Тем самым они оказываются

способными

пережать

«фазу

вымирания» и реплицироваться

дальше. Маловероятные события становятся необходимыми

большой популяции.

Образовавшиеся короткие цепи РНК свертываются в третич-

ные

структуры. Мы знаем, что молекулы

тРНК

обладают ком-

пактной

третичной структурой [56]. Возникает дивергентная

фаза

эволюции — набор различных третичных

структур

пра-

РНК,

различных мутантов. Среди мутантов имеются более

устойчивые к гидролизу. Через некоторое число п периодов син-

теза и распада сохранятся и размножатся преимущественно эти

мутанты

пра-РНК-

Условие селекции состоит в том, что следую-

щая

ошибка репродукции возникает в среднем не ранее чем че-

рез п периодов.

Если

Z есть число нормальных молекул, приходящихся па

один

мутант, то вероятность его появления есть 1/Z. В п

поко-

лениях нет ошибок репродукции. Вероятность появления новой

ошибки

равна Р, т.е. после \/Р поколений каждый потомок му-

9.6. ТЕОРИЯ ПЕРЕХОДА К БИОЛОГИЧЕСКОЙ ЭВОЛЮЦИИ 505

танта содержит ошибки. Будем считать для простоты, что

1/Р поколениях после первого появления выгодного мутанта

ошибок

нет, а затем они появляются, п есть число поколений,

обеспечивающее превращение мутанта в исходную форму. Если

\/Р < п, мутант вымирает. При 1/Р > п вся популяция стано-

вится мутантной. Оптимальная вероятность ошибок репродукции

дается условием 1/Р = п, т.е. Рп = 1. Пусть число звеньев

цепи РНК N =* 50, что примерно соответствует цепи

тРНК.

При

меньших N молекула подвергается гидролизу, при больших

синтез слишком долог. Положим Z = 10

и примем, что ве-

роятность выживания выгодного мутанта г вдвое больше ве-

роятности выживания исходной цепи, т. е. г

= Z или 2™ = 10

Находим п = 20. Условие отбора

дает

Р ^ 1/20. С

другой

сто-

роны,

Р = Nw, где w — вероятность ошибки в одном основании.

При

N = 50 ш должно быть меньше или равно 10~

. Опыт

дает,

однако,

на порядок большую величину, а именно w ~ 10~

. Сле-

довательно, должен существовать добавочный механизм отбора.

Кун

предполагает, что этот механизм обеспечивается образова-

нием

и распадом агрегатов молекул

пра-РНК.

Возникает почти

безошибочная репродукция агрегатов, несмотря на частые

ошибки

в репродукции отдельных молекул РНК. Молекулы

с ошибками агрегатов не образуют. Для агрегатов условие се-

лекции

достижимо, хотя для отдельных молекул Р = Nw =

50-10~

= 0,5. С ростом числа репликаций s в фазе синтеза

уменьшается доля экземпляров без ошибок иг — фактор пре-

имущества — убывает. Возрастание Р = Nws и уменьшение т

ведут

к обострению условий отбора. Они соблюдаются, если п

не

слишком велико, т. е. г превышает некоторую критическую

величину.

Молекулы РНК в

агрегатах

лучше защищены от гидролиза.

Для того чтобы агрегаты образовывались достаточно быстро,

подходящие молекулы РНК должны встретиться за время т, су-

щественно меньшее, чем продолжительность фазы вымирания,

которую можно считать равной одному дню. Это может быть до-

стигнуто путем компартментализации. Если она реализуется

результате

попадания молекул

пра-РНК

в водную

среду

ме-

жду частицами глины, занимающую объем порядка размеров

клетки

V ~ 10~

см

, то время, необходимое для образования

агрегата, можно оценить из коэффициента диффузии. По оценке

Куна

образование линейного агрегата из 20 молекул

пра-РНК

требует

1 час. Это время может оказаться значительно меньше,

если

агрегат

представляет собой компактную молекулу РНК,

служащую

для нуклеации агрегата, и присоединенную к ней

цепь

(пра-мРНК),

служащую

направляющей для сборки линей-

ного агрегата (рис. 9.6), т. е. для объединения пра-тРНК. В этом

случае

трехмерная диффузия заменяется одномерной.

506 ГЛ. 9. ПРОБЛЕМЫ РАЗВИТИЯ

Таким образом, в принципе возможен устойчивый отбор агре-

гатов РНК без участия белков, т. е. без гиперциклов по Эйгену.

В модели Куна реализуется ценность информации всей цепи

пра-РНК

как при возникновении третичной ее структуры, так

при образовании агрегатов.

Предположим далее, что поверхности отобранных линейных

агрегатов способны катализировать поликонденсацию активи-

рованных аминокислот в пептидные цепи. Это

дает

селекцион-

ные преимущества — агрегаты стабилизуются

пептидными молекулами. Ошибки реплика-

ции

могут

оставлять неизменными контакт-

0 \]

ные, каталитические, участки поверхности.

. Частицы глины (монтмориллонита) также ка-

' тализируют образование полипептидов [57].

П\

s~~xr~\D

Здесь возникает поворотный пункт — си-

^^^\\l)

стемы образуют полипептидные оболочки и

становятся поэтому независимыми от внеш-

{ него компартмента (см. опыты Фокса по об-

разованию протеиноидных микросфер [38]).

—ту—^г П Линейный агрегат, состоящий из пра-мРНК

V V и пра-тРНК, играет роль пра-рибосомы.

{ Наступает новая конвергентная фаза — си-

стема, которая быстрее строит свою обо-

лочку, имеет селекционные преимущества. Без

образования оболочки были бы невозмож-

Рис.

9.6. Модель ны переходы на следующие ступени эво-

сборки агрегата из люции

молекул пра-РНК г\

по

Куну. Описанная ситуация должна возникать в

достаточно больших популяциях пра-РНК.

Пра-рибосомы эволюционируют далее — скорость продукции

полипептидов оболочки растет вследствие более точного узна-

вания

аминокислот контактными участками пра-тРНК.

Возникновение кода начинается предположительно с узна-

вания

цепью пра-мРНК частиц пра-тРНК. В начале узнается

лишь средний нуклеотид триплета, т. е. имеются четыре сорта

пра-тРНК.

Узнавание означает лучший контакт

между

молеку-

лами и способствует сборке агрегата. Тем самым создается код

для четырех аминокислот, но он еще не фиксирован. Форма,

случайно синтезирующая особенно полезный полипептид, не мо-

жет еще отбираться из-за частых ошибок репликации. Но если

полипептид случайно оказывается РНК-репликазой, то вероят-

ность ошибки может понизиться по оценке Куна с 10~

до 10~

Такая система имеет автокаталитические свойства и получает

селекционные преимущества — увеличенный фактор преимуще-

ства при размножении г. Информация, заложенная в специфи-

ческой последовательности аминокислот, консервируется, и фик-

9.6. ТЕОРИЯ ПЕРЕХОДА К БИОЛОГИЧРХКОЙ ЭВОЛЮЦИИ 507

сируется код для

четырех

аминокислот или, что более суще-

ственно,

для

четырех

групп аминокислот. Дивергентная фаза

эволюции

переходит

при этом в конвергентную. Происходит се-

лекция

систем, синтезирующих полипептиды с избранной после-

довательностью аминокислотных остатков.

постепенно образуются ферменты — аминоацил-синте-

тазы для

четырех

пра-тРНК, что повышает специфичность свя-

зывания

аминокислот. Как только вероятность ошибки стано-

вится меньше критического значения, дальнейшая эволюция

происходит с необходимостью. Очевидно, что опасны ошибки

среднем нуклеотиде антикодока. Но после того, как возникла

форма,

способная к ферментативной репликации с малым чис-

лом ошибок, ошибка в антикодоне перестает быть суще-

ственной.

Каждый индивидуум с такой ошибкой синтезирует

неправильный

полипептид и в дальнейшей эволюции не уча-

ствует.

Таким

образом, должен реализоваться

переход

к системе,

служащей новым целям.

Аппарат

синтеза неспецифических по-

липептидов, образующих оболочку,

улучшается

и приводит к си-

стемам с полипептидами, обладающими определенными после-

довательностями остатков. Это означает новые возможности

химического поведения. На той же стадии фиксируется хираль-

ность аминокислот. В сущности, создается примитивный орга-

низм

— пра-клетка.

Последующий отбор означает выживание систем с наилуч-

шими

ферментами. Уменьшается вероятность синтеза «бессмыс-

ленных»

белков. На этом этапе начинает играть роль первый

нуклеотид антикодона. Однако эволюции мешает образование

комплементарных нитей РНК, не

участвующих

в синтезе бел-

ков.

Рано или поздно случайно возникает белок, катализирую-

щий

образование ДНК на матрице РНК, что ускоряет размно-

жение.

Таким образом, предполагается возникновение

РНК-за-

висимой

ДНК-полимеразы. В дальнейшем, после включения

ДНК

в генетический аппарат, этот фермент более не нужен, но

должна функционировать транскриптаза. Цепи ДНК объеди-

няются

посредством лигаз, создается геном. Сосредоточение

всего информационного плана в ДНК

дает

селекционные пре-

имущества, так как уменьшаются нарушения синтеза из-за по-

тери тех или иных

мРНК

и облегчается решение проблем взаи-

мосвязи

структуре

системы. Репликация ДНК обеспечивает

умножение матрицы и, следовательно, добавочное селекционное

преимущество.

результате

перечисленных событий возникает «машина»,

которой инструктированные белки «подогнаны

друг

другу»,

как

колесики в часовом механизме. Практически каждая ошиб-

ка

останавливает

работу

всей системы.

508 ГЛ. 9.

ПРОБЛЕМЫ

РАЗВИТИЯ

Кун

предлагает

грубую

оценку времени, необходимого для

инструктирования 10

белков, что

соответствует

содержанию

белков в одной бактериальной клетке.

Заметные селекционные преимущества возникают лишь в тех

случаях,

когда у вновь инструктируемых белков по крайней

мере v мест занято надлежащими остатками. Соответственно 3v

кодонов

должны располагаться правильно (вырождение кода

уменьшает это число). Вероятность найти определенное основа-

ние

в 3v местах есть ('Д)

^ Следовательно, предельное допусти-

мое число мутаций — одна мутация на Z = 4

особей. Фактор

преимущества г находится из условия п = In Z/ln г. Если уже

имеется репликационная система, работающая с оптимальной

частотой ошибок, то

п = 1/р = 1/wN

Примем,

что каждый добавочный белок

дает

селекционные пре-

имущества, в частности, повышает шансы на выживание при-

мерно

на 20% (г = 1,2). Величина г должна сильно возрастать

с v. Допустим, что это возрастание экспоненциально, т. е. г =

exp(v/a). Если при v = 300 г = 1,2, то а = 500;

тогда

при

v = 5 г

=1,01.

Примем v = 5, N = 10

, что

соответствует

белку из 300 аминокислотных остатков. Следовательно,

«10

rt=ln

/ln

1,01 « Ю

o)»10~

Инструктирование всего белка есть процесс оптимизации. Он

требует,

чтобы сменилось

q = N/(3vw)

поколений

(принято, что за N/(3v) последовательных шагов ин-

структируется v аминокислот, 1/ш — число поколений, соответ-

ствующее одной ошибке в каждом кодоне). Находим q ~ 10

поколений.

За это число поколений ДНК удлиняется на 10

нуклеотидов. Число поколений, нужных для инструктирования

белков, равно

Если

новое поколение возникает каждые 20 мин, то время, тре-

буемое

для эволюции до уровня сложности бактериальной

клетки,

равно по порядку величины 10

— 10

лет, если на одно

поколение

нужны сутки, то оно составляет

—10

лет. Вели-

чина

Q слабо зависит от г. Эволюция идет тем быстрее, чем

больше популяция, т. е. число Z.

9.7.

ФИЗИКО-ХИМИЧЕСКИЕ

ОСНОВЫ

ЭВОЛЮЦИИ

509

Таким образом, согласно оценкам Куна, эволюция вполне

могла осуществиться за время, протекшее с эпохи возникнове-

ния

жизни на Земле.

Дальнейшая эволюция — возникновение многоклеточных ор-

ганизмов из одноклеточных и возникновение всего многообразия

видов — связана с возможностью слияния систем с различными

белками. Можно привести соображения в пользу того, что это

требовало меньшего времени, чем создание первых клеток (см.

ниже).

Дальнейшее обсуждение проблем, рассмотренных в из-

ложенной работе Куна, приведено в следующем параграфе.

В работе [58] выполнены расчеты, иллюстрирующие описанную

модель эволюции.

Чернавский и Чернявская предложили несколько отличную

модель [59] (подробное изложение см. в [90]). В этой работе

проведен строгий анализ основных положений теории и развита

математическая теория самоорганизации макромолекул, хими-

ческой и биологической эволюции, основанная на анализе устой-

чивости возникающих состояний системы. В расчетах исполь-

зуется метод фазовых портретов. Важным моментом этой теории

является предположение об антагонистических взаимодействиях

между

равноправными объектами, описываемых уравнением

= axi — b X х

{

(9.37)

где а, Ъ > 0. Наличие антагонистических взаимодействий озна-

чает нелинейность, которая может вести к эволюции. Анализ

уравнений типа

(9.37)

приводится ниже.

§ 9.7. ФИЗИКО-ХИМИЧЕСКИЕ ОСНОВЫ БИОЛОГИЧЕСКОЙ ЭВОЛЮЦИИ

ЦЕННОСТЬ ИНФОРМАЦИИ

Модельная теория Куна, изложенная в предыдущем пара-

графе, естественно, не претендует на то, чтобы реконструиро-

вать истинный путь эволюции на Земле. Как пишет Кун, задача

теории состоит в том, чтобы «описать модель, эксперименталь-

ная

проверка которой позволяет лучше познать принципы, важ-

ные для эволюции» [55]. Эта модель основана на действительно

важных принципах. Первый принцип — необходимая реализа-

ция

маловероятных событий в больших популяциях, размножаю-

щихся в открытой системе, далекой от равновесия. Второй

прин-

цип

— определяющее значение ценности информации при воз-

никновении

вторичной и третичной структуры, агрегации и т. д.

Третий принцип — организующее значение периодичности, на-

личие чередующихся стадий синтеза и распада, определяемых

сменой дня и ночи. Последний принцип впервые введен в рас-

смотрение в работе Куна.

510 ГЛ. 9. ПРОБЛЕМЫ РАЗВИТИЯ

Остановимся на втором принципе. Ценность информации, со-

держащейся в макромолекуле в соответствии с теорией Эйгена,

можно представить селективной ценностью, выражаемой через

кинетические

параметры. Для осуществления эволюции кинети-

ческие процессы должны быть автокаталитическими и, тем са-

мым,

нелинейными. Здесь важно положение, отмеченное на

стр. 494: автокатализ должен определяться узнаванием

доста-

точно протяженной системы мономерных звеньев, а не отдель-

ных звеньев. Только при этом условии селективная ценность об-

ретает

смысл ценности информации, заложенной в макромоле-

кулярной

цепи.

Ценность

информации впервые появляется в модели Куна

при

рассмотрении селекции D- или L-рибозы, необходимой для

образования

стереоспецифической цепи пра-тРНК, обладающей

определенной вторичной структурой. Тем самым, возникновение

хиральности считается очень ранним событием. В принципе по-

явление хиральности можно отнести и к более поздней стадии.

Преимущество хиральности для структурирования РНК оче-

видно,

однако необходимо объяснить, каким образом хираль-

ность может быть зафиксирована. Вообще говоря, возможно од-

новременное

образование

двух

энантиомерных популяций, одна

из

которых состоит из D-звеньев, а

другая

— из L-звеньев. В це-

лом система рацемична, подобно, например, месторождению

кристаллического кварца, в котором встречаются с равной ве-

роятностью правые и левые кристаллы. Однако при случайном,

флуктуационном превышении численности одной развивающейся

популяции

над

другой

возможно эволюционное предпочтение

первой популяции и ее преимущественное развитие (ср. [33]).

Приведем иллюстративные расчеты.

Пусть Х\ и х

— числа молекул

пра-РНК

в системе, построен-

ных соответственно из D- и L-мономеров, обозначаемых т.\ и т

Скорости

образования Х\ из т

и х

из т

одинаковы, одина-

ковы

и скорости их распада. Кинетические уравнения, описы-

вающие развитие системы, имеют вид

Xy —

XXiWi

— lX\, )

. \

(9.38)

— лх

, )

где х и % — константы скоростей полимеризации и распада со-

ответственно, а

Ш] + т

— вероятности встречи матриц 1 и 2 соответственно с мономе-

рами т,\ и т

. При

любых

значениях mi и т

= xi

(0)

ехр

[{%

—

2К)

/].

(9.39)