Волькенштейн М.В. Общая биофизика

Подождите немного. Документ загружается.

9.3. ТЕОРИЯ ДОБИОЛОГИЧЕСКОЙ ЭВОЛЮЦИИ 491

талитическое усиление приводит к макроскопическому проявле-

нию

случайных микроскопических событий. Сам процесс роста

численности подвержен статистическим флуктуациям, которые

должны учитываться. Эйген провел вероятностное рассмотрение

проблемы [43], основываясь на стохастической теории процессов

рождения и гибели (см. [45]). Стохастические модели представ-

ляют собой в данном

случае

цепи Маркова [43—46]. Детерми-

нистическая

теория соответственно модифицируется. Рассмотрим

вслед за Эйгеном три примера.

Допустим, что имеется п различных носителей информации,

причем каждый из них представлен одной цепью. Редупликация

точная,

все Q

= 1. Все F

{

и R

одинаковы, т.е. W

= Е

Со-

гласно детерминистической теории в системе не

будет

никаких

изменений.

Стохастическая теория показывает, однако, что си-

стема

будет

утрачивать информацию при распаде каждого неиз-

быточного носителя, происходящем до его редупликации. Со-

держание информации сузится до немногих или

даже

одной

сильно

избыточной последовательности, а затем вся популяция

вымрет вследствие «флуктуационной катастрофы». Это неиз-

бежно, так как флуктуации образования и распада цепей неза-

висимы.

Полное вымирание произойдет достаточно быстро —

стационарная

популяция, состоявшая при t = 0 из п видов,

среднем просуществует в течение времени n/F < t < n

/F. Нет

критерия

выживания, кроме самого выживания, нет оптимиза-

ции.

Если

система та же, все Wi одинаковы, но Q, < 1, то

судьба

всей популяции

будет

такой же. Однако поведение отдельных

носителей информации

будет

иным. Если A

= D,- и Q,- < 1, то

AiQi

— Di < 0. Это вымирание компенсируется продукцией

новой

информации вследствие ошибок копирования. Система

«беспорядочно дрейфует в информационном пространстве», но

конце концов уничтожается «флуктуационной катастрофой».

Лишь при Wi ф W

и Qi < 1 реализуется устойчивое вос-

произведение и отбор цепей с максимальным значением W

Пока

эти цепи образовались в малом числе, они подвергаются

опасности

вымирания вследствие флуктуации. С ростом их числа

система становится более устойчивой и, в конце концов, главные

копии

доминируют в соответствии с детерминистической тео-

рией.

В этом

случае

система

ведет

себя сходно с системой, на-

ходящейся в устойчивом равновесии, в котором флуктуации,

пропорциональные

л/п, несущественны для больших значе-

ний

п. Однако при образовании системы каждое макросостоя-

ние

вырастает из микросостояния, представленного вначале

единичной

копией. Следовательно, для таких метастабильных

систем детерминистическое поведение ограничено гораздо силь-

нее,

чем для систем, близких к истинному равновесию.

492

ГЛ. 9.

ПРОБЛЕМЫ

РАЗВИТИЯ

Следует

остановиться на информационных аспектах описан-

ной

модели самоорганизации и эволюции информационных мак-

ромолекул. Работе Эйгена предшествовала работа Кастлера,

имеющая близкое название — «Возникновение биологической

организации» [88]. Приведем пространную цитату из этой ра-

боты: «В добиологической полинуклеотидной системе почти все

последовательности оснований равноправны. Отсюда

следует,

что такая последовательность сама по себе не имеет никакого

«смысла»,

т. е. не несет никакой информации, являясь лишь

«шумом»...

Вместе с тем исходная «бессмысленная» последова-

тельность становится весьма осмысленной, как только возникает

необходимость точно следовать ей. Информация возникла бла-

годаря

тому,

что какая-то одна определенная нить стала праро-

дительницей системы, т. е. она возникла благодаря стабильности

системы, порожденной этой особой нитью.

Следует

подчеркнуть,

что возникновение информации из шума — это совсем не то, что

обнаружение информации, замаскированной шумом, например

при

выявлении ранее не известной закономерности... Запоми-

нание

случайного выбора служит механизмом создания

инфор-

мации,

и по своей природе этот механизм совершенно отличен

от механизма обнаружения информации».

В свете этих представлений теория Эйгена оперирует не со-

зданием новой информации, но обнаружением ранее существо-

вавшей, поскольку главная копия закономерно обладает наи-

большей селективной ценностью. Отбор идет не по количеству,

но

по ценности информации.

В моделях, основанных на рассмотрении неустойчивых со-

стояний

(см. далее, стр. 501, 512), фигурирует уже не выявле-

ние

ранее существовавшей информации, но ее возникновение в

результате

случайной флуктуации в начальных условиях.

Вопрос о ценности информации рассмотрен далее (см.

стр. 514).

9.4.

ПОЛИНУКЛЕОТИДНЫЕ

ПОЛИПЕПТИДНЫЕ

СИСТЕМЫ

Экспериментально установлено матричное автокопирование

полирибоадениловой кислоты при низких рН, а также автоко-

пирование

полирибоцитидиловой кислоты. Представим себе ав-

токопирование

нуклеиновой кислоты с X разных нуклеотидов.

Считая

узнавание равновесным, имеем

Вероятность

пары ii

Сумма

вероятностей для

всех

пар *•

где Кн, = ехр(—SGiJRT)—константы равновесия, \G

— сво-

бодные энергии

9.4. ПОЛИНУКЛЕОТИДНЫЕ И ПОЛИПЕПТИДНЫЕ СИСТЕМЫ 493

В природе, однако, происходит не автокопирование, но ком-

плементарное копирование нуклеиновых кислот. В этом

случае

система описывается чередованием плюс- и минус-копий -Ц и

—L

Отбор происходит среди коллективов ±г, представляемых

циклами

Теория

в принципе не изменяется. В этом

случае

существенно,

что

даже

при большом избытке одного мономера система долж-

на

накопить по меньшей мере два разных мономера, которые

затем встречаются у отобранного вида в почти равных количе-

ствах.

Вследствие копирования ошибок система всегда образует

смешанные последовательности. Это служит предпосылкой для

возникновения

любого кода, который может приобрести

«смысл»,

если каждая из смешанных последовательностей

дает

селектив-

ное

преимущество для самовоспроизведения.

Однако неферментативное узнавание не является вполне точ-

ным,

значения

порядка 3 ккал/моль и факторы q не пре-

вышают 0,99 (ср. стр. 488). Соответственно, воспроизводимое

образование нуклеотидных цепей возможно лишь для относи-

тельно коротких последовательностей, содержащих не более

30—100

звеньев —для q = 0,99 и v = 100, Q = 1/е. Отсюда Эй-

ген

делает

вывод о невозможности достижения уровня само-

организации,

необходимого для согласованного фукционирова-

ния,

путем неферментативного матричного синтеза полинукле-

отидов.

Эта аргументация, однако, недостаточна [47]. И. М. Лифшиц

обратил внимание на то, что теория Эйгена не учитывает одного

важного обстоятельства. Селективная ценность, выражаемая

кинетическим

параметром W

не однозначно коррелирует с пер-

вичной

структурой цепи. В цепи

могут

возникать мутации и мат-

ричный

синтез может происходить с ошибками без того, чтобы

параметр W

изменился. Матричная редупликация основана на

узнавании отдельных единиц и их ближайших соседей. Таким

образом, например, двойная мутационная замена

...CABBD ... CACBD ... -> ... CACBD ... CABBD ...

не

должна сказываться на значении W

т. е. на скорости син-

теза цепи как целого.

Двойная

мутация, конечно, маловероятна. Единичная замена

звена меняет W*, но при большом числе звеньев v это измене-

ние

очень мало. Относительное изменение скорости матричного

494 ГЛ. 9. ПРОБЛЕМЫ РАЗВИТИЯ

синтеза при замене одного звена имеет порядок величины v~

Допустим, что в

результате

замены W

увеличилась на соответ-

ствующую

малую

величину. Селекция

требует

времени. Если за

время преимущественного выживания главных копий появится

вторая мутация, возвращающая Wi к прежнему значению, то но-

вая

главная копия не возникает. Следовательно, селективная

ценность

Wi не выражает ценности информации в

случае

про-

стой или комплементарной репродукции.

Как

бы ни были малы вероятности мутаций и ошибок

реду-

пликации,

через достаточное время в системе

будут

накапли-

ваться цепи, вырожденные по значению W

, но разнящиеся пер-

вичной

структурой. Если цепи достаточно длинны, то число та-

ких вырожденных макромолекул станет очень большим. В ко-

нечном

счете наиболее вероятному состоянию системы

будет

соответствовать максимальное разнообразие первичных струк-

тур цепей с одинаковыми значениями

. Селекционное равно-

весие не только неустойчиво, но неизбежно должно вырож-

даться.

Вслед

за стадией селекции, строго рассмотренной Эйге-

ном,

наступит стадия релаксации к вырожденному состоянию.

Тем самым система

будет

не эволюционировать, но деградиро-

вать. Селекция на первой стадии еще не означает эволюции.

Для эволюционного добиологического развития необходима

автокаталитическая система, использующая информацию цепи,

т. е. репродуцируемая путем узнавания не отдельных единиц, но

всей первичной структуры. Такая система также рассмотрена

Эйгеном.

Полипептидные

цепи, белки, также

могут,

в принципе, обра-

зовать самоинструктируемые системы. Белки характеризуются

значительно большей точностью узнавания определенных суб-

стратов благодаря наличию пространственной структуры и зна-

чительно большим объемом информации. Показано, что полный

синтез полипептида, например грамицидина S, представляющего

собой циклический декапептид, возможен с помощью одного

фермента, без участия нуклеиновых кислот [48]. Фермент функ-

ционирует как белковая матрица, соединяя активированные

АТФ аминокислоты в точную последовательность

О-Фен-Ь-Про-Ь-Вал-Ь-Орн-Ь-Лей

(Орн

— орнитил), которая остается прикрепленной к ферменту,

пока

два законченных пентапептида не соединятся с образова-

нием

циклической молекулы грамицидина S. Однако для само-

воспроизведения белка требуется ряд

других

белков-ферментов.

Например,

если фермент узнает последовательность из 5 амино-

кислот, то для синтеза цепи с 80 пептидными связями требуется

не

менее 5 ферментов

-£i*

5 —

•>

10-^> 20 -^> 40 —

80.

9.4.

ПОЛИНУКЛЕОТИДНЫЕ

ПОЛИПЕПТИДНЫЕ СИСТЕМЫ

495

Чем больше ферментов

такой цепи,

тем

больше вероятность

образования

замкнутого автокаталитического цикла. Независи-

мые циклы

ведут

себя

как

самоинструктируемые

или

компле-

ментарные коллективы.

Они

могут

быть взаимозависимы вслед-

ствие полифункциональности ферментов

— в

этом

случае

ото-

бранный

вид с

максимальной

несет

за

собой

все

связанные

ним

ветви

циклы. Разветвление циклов означает бесполез-

ный

для

саморепродукции балласт,

пони-

жающий

Wi.

Наиболее существенное

пре-

пятствие саморепродукции ферментных

циклов

состоит

в том, что

способность

уз-

навания

является свойством

не

любых,

лишь

уникальных цепей,

обусловлена

ред-

ким

совпадением специальных функцио-

нальных свойств различных белков. Поэто-

^ у

му белки, катализирующие свою репродук-

цию

специфических циклах, неспособны

Рис

Репродукция

репродуцировать мутантные цепи,

даже

ТитГеском'цГлГ'

дающие преимущества.

На рис. 9.2

изобра-

жен цикл, оставшийся

результате

отбора. Пусть Е'.

— му-

тант.

Для

эволюции недостаточно того,

что Е[ —

лучший ката-

лизатор,

чем Е\, так как он

по-прежнему

будет

репродуциро-

вать

, . .. , Е

приведет снова

к Е\, а не к Е[. Для

повыше-

ния

селективной ценности цикл должен испытать

ряд

специфи-

ческих мутаций

Е^Е', Е

^-Е'

, ...,

-+Е'

т.е.

образовать

новый

цикл. Вероятность такого события ничтожно мала.

Си-

стема

не

может использовать селективные преимущества,

бу-

дучи

нагружена слишком большим количеством информации,

имеющей

малую

селективную ценность.

Из

приведенных рассуждений

следует,

что ни

нуклеиновые

кислоты,

ни

белки сами

по

себе

не

могут

обеспечить самоорга-

низацию.

Эйген считает необходимым

для

этого комбинацию

свойства инструктируемой комплементарной репродукции

ну-

клеиновых кислот

большой информационной емкостью белков,

т.

е.

гиперцикл, содержащий

оба

типа информационных макро-

молекул.

Рассмотрим самоинструктируемый каталитический

гиперцикл

(рис.

9.3) и

перечислим

его

свойства:

1. Каждый гиперцикл способен

автокаталитическому

росту.

2. Независимые циклы конкурируют

подвергаются

от-

бору.

3. Вследствие нелинейности отбор очень жесткий.

4. Система способна использовать малые селективные

пре-

имущества

быстро эволюционировать.

496

ГЛ.

ПРОБЛЕМЫ РАЗВИТИЯ

5. Реплицируемая длина отдельной кодирующей единицы

должна быть достаточно мала, чтобы обеспечить воспроизводи-

мость.

6. Генотипические мутации,

т. е.

изменения

в /,-,

могут

не-

медленно использоваться ферментом

£,-ь

При

конкуренции нуклеиново-белковых гиперциклов

не дол-

жна возникать деградация, описанная

на стр. 494. В

гиперцикле

используется ценность информа-

ции

цепи

РНК или ее

участка,

так

как она

определяется

спо-

собностью программировать

син-

тез белковой цепи

£,-.

Модельные количественные

расчеты проведенные

помощью

ЭВМ

(см.

[44]),

подтверждают

эти

положения.

Очевидно,

что

гиперцикл

воз-

можен лишь

при

наличии нуклео-

тидно-аминокислотного кода.

Во-

прос

о том, как

этот

код

возник,

требует

специального рассмотре-

ния.

Современный

код

обладает

высокой помехоустойчивостью

по

отношению

мутациям, сильно

искажающим биологически функ-

циональную пространственную

структуру

(см. [7], § 9.7). Код

универсален. Маловероятно,

что

он

развился

из

предшествую-

щего синглетного

или

дублет-

ного кода. Изменение величины

кодона повлекло

бы за

собой полную потерю ранее накоплен-

ной

информации

[49].

Наиболее существен центральный нуклео-

тид кодона. Восемь кодонов, содержащих

А и У,

отвечают

го-

раздо большему разнообразию аминокислот,

чем

восемь кодо-

нов,

содержащих

Г и Ц.

Смысл узнавания аминокислоты

тРНК,

несущей антикодон,

до

сих пор не

ясен. Несомненно,

что в

этом узнавании суще-

ственную роль играет фермент аминоацил

—

тРНК-синтетаза.

Эйген ставит законный вопрос:

«если

специфические взаимодей-

ствия

отсутствуют,

то не

могло

ли

однозначное кодовое соот-

ветствие появиться

из

случайных комбинаций аминокислот

с ан-

тикодонами?»

[44].

Допустим,

что

имеется

единиц аминокислоты

а, Ь, с, ...,

которым

соответствуют

кодоны

А, В, С ...,

соединяющиеся

а,Ь,с...

при

посредстве комплементарных адапторов

Рис.

9.3. Самоинструктируемый

каталитический гиперцикл.

— носители информации,

т. е.

±/-цик-

лы РНК;

£»

—ферменты, кодируемые

катализирующие образование носи-

теля

/<_J.J;

•,

В, и т. д.

—ферменты,

катализирующие паразитные процессы.

9.4. ПОЛИНУКЛЕОТИДНЫЕ И ПОЛИПЕПТИДНЫЕ СИСТЕМЫ 497

Л', В', С ... Имеется X

таких соответствий, например, при Х=2

аА, аВ, ЬА, ЬВ (если все соответствия равновероятны). Рассмо-

трим элемент объема, в котором имеется X таких соответствий.

Вероятность найти данный набор соответствий обратно пропор-

циональна

числу

всех

возможных наборов, равному числу

всех

сочетаний с повторениями из X

элементов по X

Среди

всех

соответствий имеется Х\ уникальных, т. е. таких,

которых данная аминокислота соответствует только одному

кодону и наоборот. Вероятность р существования элемента

объема, в котором имеется какое-либо уникальное соответствие,

равна

_ AI

(Я1)

(Я

1)1

рХ

со

(Я,

+ Я

—1)!

В таком элементе объема может начаться трансляция нуклео-

тидных последовательностей в аминокислотные. Чтобы этот про-

цесс стабилизовался, среди нуклеотидных последовательностей

должны иметься такие, которые усиливают использование того

же кода после трансляции. Должен возникнуть самоусиливаю-

щийся

гиперцикл. При близости концентраций случайных нук-

леотидных последовательностей и концентраций случайных по-

липептидов вероятность р' нахождения определенного набора

нуклеотидов также обратно пропорциональна со. Совместная ве-

роятность равна приближенно

При

X — 4 имеем р'= 1,6- Ю-

, при X = 8 получим р'= 4- 10~

1в

Конечно,

эта формула

дает

лишь

грубую

оценку.

Как

показывают опыты Фокса [38, 39], данная функция белка

может реализоваться большим числом разных полипептидных

последовательностей. Вероятность совпадения функций, а не

последовательностей, оказывается более высокой.

Система восьмибуквенного кода, построенного из А и У,

обеспечивает отбор восьми аминокислот, что достаточно для

широкой

функциональности белков. Возможно, что современный

код начался со случайной флуктуации — код является след-

ствием нелинейной конкуренции, обеспечивающей его универ-

сальность.

Эйген

сравнил свою теорию с результатами опытов Шпигель-

мана

по эволюции з пробирке [50—52]. Qp-фаг использует для

своего размножения специфический фермент Qp-репликазу, уз-

нающий

только РНК. этого фага. Qp-репликаза и активированные

498 ГЛ. 9. ПРОБЛЕМЫ РАЗВИТИЯ

мономеры, нуклеозидтрифосфаты помещались в пробирку, в

которую в качестве затравки, матрицы, вводилось малое ко-

личество Qp-PHK- Происходил матричный репликационный син-

тез РНК- Малая доля синтезированной РНК переносилась в ка-

честве матрицы в

следующую

пробирку, содержащую репликазу

мономеры, и т. д. При этом постепенно уменьшалось время ин-

кубации реакционной смеси. Тем самым отбирались лишь те

цепи

РНК, которые быстрее всего реплицируются.

Утрата

спо-

собности воспроизводить Qp-фаг, т. е.

утрата

инфекционности,

происходила уже после четвертого переноса. Матричный синтез

РНК,

однако, продолжался, и после 80 переносов получались

молекулы РНК, утратившие до 85% своих исходных звеньев, но

по-прежнему взаимодействующие с репликазой. Ферментатив-

ный

матричный синтез РНК использует ценность информации,

содержащейся не менее чем в 15% исходной цепи. Теория Эй-

гена

дает

прекрасное количественное описание этих эволюцион-

ных опытов [43, 44].

Какова

дальнейшая

судьба

случайно возникших и далее под-

вергающихся естественному отбору нуклеиново-полипептидных

гиперциклов? В такой системе отбор происходит против пара-

зитных цепей, если селективные ценности последних меньше,

чем у членов цикла. Паразитные цепи с высокими селективными

ценностями не

дадут

возможности циклу пройти стадию нуклеа-

ции,

если они имеются с самого начала. Напротив, если эти

ветви возникли после нуклеации, то они не имеют шансов расти

вследствие нелинейности селекционного поведения. С гиперцик-

лом

могут

сосуществовать лишь ветви, селективные ценности

которых такие же, как для гиперцикла. Точное совпадение воз-

можно лишь, если ветвь и кодирующий участок /, внутри цикла

используют один и тот же промотор, локализованный в Е^

Отсюда

следует

генная и регуляторная

структура

кодовой си-

стемы.

После нуклеации гиперцикл должен пространственно обосо-

биться от среды. Компартментализация необходима для исполь-

зования

функциональных ветвей, возникших вследствие

мута-

ций.

Компартментализованная система может «индивидуализи-

роваться» путем соединения своих кодирующих единиц в

единую цепь и воспроизводить всю эту цепь. В такой цепи, ко-

торая при участии лигаз

будет

циклической, гены, происхо-

дящие от данной единицы /,-, локализуются в соседних поло-

жениях.

Эти свойства гиперциклов означают, в сущности, переход

клетке — к следующей стадии эволюции (см. далее).

Ряд поучительных модельных расчетов, основанных на тео-

рии

Эйгена, проведен Эбелингом [89] (см. также [170]).

9.5.

ТЕРМОДИНАМИКА

ЭВОЛЮЦИЯ

499

9.5.

ТЕРМОДИНАМИКА

ЭВОЛЮЦИЯ

Теория Эйгена согласуется с термодинамикой нелинейных не-

обратимых процессов (см. гл. 2 и 8). При постоянных потоках

стационарное состояние характеризуется относительным мини-

мумом производства энтропии. Такому состоянию соответствует

доминирование отобранных гиперциклов. Если произошла сто-

хастически значимая мутация, состоящая в возникновении му-

танта с большей селективной ценностью, то это означает появ-

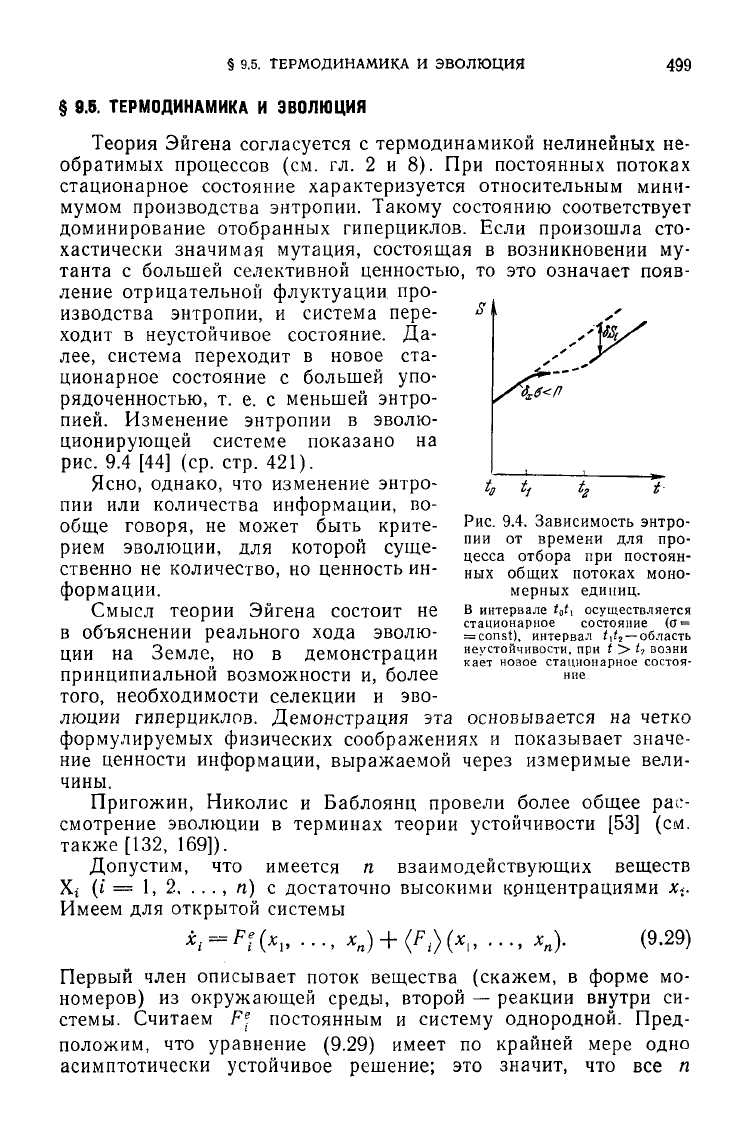
ление отрицательной флуктуации про-

изводства энтропии, и система пере-

ходит

в неустойчивое состояние. Да-

лее, система переходит в новое ста-

ционарное состояние с большей упо-

рядоченностью, т. е. с меньшей энтро-

пией.

Изменение энтропии в эволю-

ционирующей системе показано на

рис.

9.4 [44] (ср. стр. 421).

Ясно,

однако, что изменение энтро-

пии

или количества информации, во-

обще говоря, не может быть крите-

Рис

- Зависимость энтро-

рием эволюции, для которой суще-

ственно не количество, но ценность ин-

формации.

пии от времени для про-

цесса

отбора

при постоян-

ных

общих

потоках

моно-

мерных

единиц.

СМЫСЛ Теории Эйгена СОСТОИТ Не В

интервале

осуществляется

стационарное состояние

(ст^

Объяснении

реаЛЬНОГО

ХОДа

ЭВОЛЮ-

onst)

интервал

/^-область

ции

на Земле, но в демонстрации ^^Г^цГарн^еСто"-

принципиальной

возможности и, более ние

того, необходимости селекции и эво-

люции гиперциклов. Демонстрация эта основывается на четко

формулируемых физических соображениях и показывает значе-

ние

ценности информации, выражаемой через измеримые вели-

чины.

Пригожий,

Николис и Баблоянц провели более общее рас-

смотрение эволюции в терминах теории устойчивости [53] (см.

также [132, 169]).

Допустим, что имеется п взаимодействующих веществ

Xj (i = 1, 2, . . . , п) с достаточно высокими концентрациями х.

Имеем для открытой системы

Первый член описывает поток вещества (скажем, в форме мо-

номеров) из окружающей среды, второй — реакции внутри си-

стемы. Считаем F

. постоянным и систему однородной. Пред-

положим, что уравнение

(9.29)

имеет по крайней мере одно

асимптотически устойчивое решение; это значит, что все п

500 ГЛ. 9. ПРОБЛЕМЫ РАЗВИТИЯ

корней

характеристического уравнения имеют отрицательные

действительные части.

Допустим теперь, что случайно возникают мутанты веществ

Xf, т.е. их ошибочные копии Yj (/= 1, •••, s) с концентра-

циями

уj. Порядок уравнений (9.29) возрастает на s. Если s=l

(один

мутант), то характеристическое уравнение увеличенной

системы

будет

содержать дополнительный член порядка е. При

малом е характеристическое уравнение

будет

иметь п -\- 1 кор-

ней,

причем п корней

будут

близки к корням системы (9.29). На

устойчивость стационарного состояния увеличенной системы бу-

дет влиять лишь новый корень

со„+ь

который может зависеть

от е либо как

i~e-\ (9.30)

если поправочный член является множителем в члене, содержа-

щем (п + 1)-ю степень ш, либо как

е, (9.31)

если появление Y,- добавляет постоянный член в характеристи-

ческом уравнении. В результате в обоих случаях

могут

возник-

нуть корни с положительной действительной частью. Малое воз-

мущение системы (9.29) может привести к существенному из-

менению

ее стабильности. В случае (9.30) это изменение

будет

очень быстрым, в случае (9.31)—очень медленным. В случае

(9.30) эволюция Y описывается уравнением

G({x},

у, г), (9.32)

уравнения (9.29) принимают вид ({х} — совокупность всех пе-

ременных Х{)

y,B).

(9.33)

При

8 = 0 последние уравнения превращаются в (9.29). В слу-

чае (9.31) уравнения (9.32) и (9.33) переписываются в виде

*/ =

G,({*})

+ eG

(W, у, в), (9.34)

= F

t (W) + (F

) ({*}) + е (F

) ({x}, у, г). (9.35)

Эти уравнения описывают эволюцию системы посредством из-

менений

устойчивости системы при добавлении новых веществ.

В частности, может возникнуть состояние, в котором вид Y бу-

дет доминирующим.

Рассмотрим случай (9.30). Введем новую временную пере-

менную т = t/e 2> t и перепишем уравнение (9.32) в виде

4f =

G({x},

у, е). (9.36)