Wai-Fah Chen.The Civil Engineering Handbook
Подождите немного. Документ загружается.


Theory and Analysis of Structures 47-31
Final moments are obtained by adding distributed fixed-end moments and 13.06/2.99 times the
distributed assumed side sway moments.
Method of Consistent Deformations
This method makes use of the principle of deformation compatibility to analyze indeterminate structures.
It employs equations that relate the forces acting on the structure to the deformations of the structure.
These relations are formed so that the deformations are expressed in terms of the forces, and the forces
become the unknowns in the analysis.
Let us consider the beam shown in Fig. 47.27a. The first step, in this method, is to determine the
degree of indeterminacy or the number of redundants that the structure possesses. As shown in the figure,
the beam has three unknown reactions, R
A
, R
C
, and M
A
. Since there are only two equations of equilibrium
available for calculating the reactions, the beam is said to be indeterminate to the first degree. Restraints
that can be removed without impairing the load-supporting capacity of the structure are referred to as
redundants.
Once the number of redundants are known, the next step is to decide which reaction is to be removed
in order to form a determinate structure. Any one of the reactions may be chosen to be the redundant,
provided that a stable structure remains after the removal of that reaction. For example, let us take the
reaction R
C
as the redundant. The determinate structure obtained by removing this restraint is the
cantilever beam shown in Fig. 47.27b. We denote the deflection at end C of this beam, due to P, by D
CP
.
The first subscript indicates that the deflection is measured at C, and the second subscript indicates that
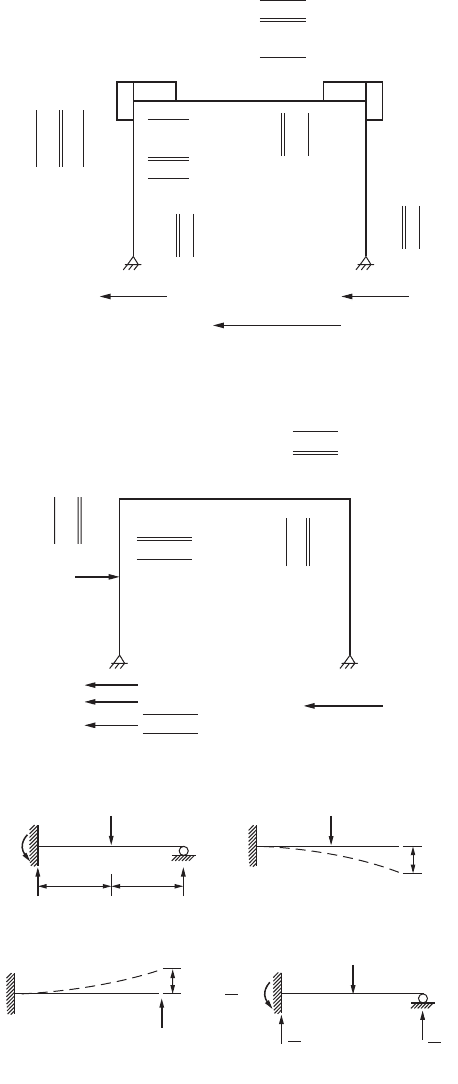
FIGURE 47.26 Example of a sway frame by moment distribution.
− 109.7
B
10
10
30
− 6.7
+ 3.8
0.64
13.06
0.57
2.44
10.00
5.50
4.50
−112.5
− 36
+ 42
0.43
+109.7
+ 0.3
−48.8
− 0.7
− 7.6
−40.5
+ 2.9
+31.5
+25
+50
−50
+50
0
0.36
D
C
A
20
20
400
1.5 (Uniformly distributed)
600
300
− 0.6
+ 0.3
48.8
− 1.2
+ 1.9
− 13.4
+21
− 72
+112.5
© 2003 by CRC Press LLC
47-32 The Civil Engineering Handbook, Second Edition
the deflection is due to the applied load P. Using the moment area method, it can be shown that D
CP
=
5PL
3
/48EI. The redundant R
C
is then applied to the determinate cantilever beam, as shown in Fig. 47.27c.
This gives rise to a deflection D
CR
at point C, the magnitude of which can be shown to be R
C
L
3
/3EI.
FIGURE 47.26 (continued).
FIGURE 47.27 Beam with one redundant reaction.
28.30
+28.5
0.57
1.59
Total
2.99
1.40
0.64
+ 7.4
− 4.2
+31.7
172.4
+ 28.8
20
10.00
1.44
8.62
11.44
−109.7
+138.5
+123.6
+ 48.8
− 28.8
−138.5
+109.7
−172.4
−123.6
− 48.8
0.43
0.36
0
−75.0
+75.0
0
−100
+100
+ 1.3
− 2.1
+14.80
+14.30
−28.3
+ 0.8
+ 8.4
+37.5
−75.0
− 31.70
− 3.2
+ 21.5
+ 50
−100
A
(a) Actual structure
M
A
R
A
R
C
L/2 L/2
BC
P
P
(d)
3
16
PL
11
16
P
5
16
P
b) Determinate structure
subject to actual loads
P
∆
CP
(c) Determinate structure
subject to redundant
R
C
∆
CR
© 2003 by CRC Press LLC

Theory and Analysis of Structures 47-33
In the actual indeterminate structure, which is subjected to the combined effects of the load P and
the redundant R
C
, the deflection at C is zero. Hence the algebraic sum of the deflection D
CP
in Fig. 47.27b
and the deflection D
CR
in Fig. 47.27c must vanish. Assuming downward deflections to be positive, we write
(47.33)
or
from which
Equation (47.33), which is used to solve for the redundant, is referred to as an equation of consistent
deformations.
Once the redundant R
C
has been evaluated, the remaining reactions can be determined by applying
the equations of equilibrium to the structure in Fig. 47.27a. Thus SF
y
= 0 leads to
and SM
A
= 0 gives
A free body of the beam, showing all the forces acting on it, is shown in Fig. 47.27d.
The steps involved in the method of consistent deformations follow:
1. The number of redundants in the structure are determined.
2. Enough redundants to form a determinate structure are removed.
3. The displacements that the applied loads cause in the determinate structure at the points where
the redundants have been removed are calculated.
4. The displacements at these points in the determinate structure, due to the redundants, are
obtained.
5. At each point where a redundant has been removed, the sum of the displacements calculated in
steps 3 and 4 must be equal to the displacement that exists at that point in the actual indeterminate
structure. The redundants are evaluated using these relationships.
6. Once the redundants are known, the remaining reactions are determined using the equations of
equilibrium.
Structures with Several Redundants
The method of consistent deformations can be applied to structures with two or more redundants. For
example, the beam in Fig. 47.28a is indeterminate to the second degree and has two redundant reactions.
If the reactions at B and C are selected to be the redundants, then the determinate structure obtained
by removing these supports is the cantilever beam, shown in Fig. 47.28b. To this determinate structure
we apply separately the given load (Fig. 47.28c) and the redundants R
B
and R
C
, one at a time (Fig. 47.28d
and e).
Since the deflections at B and C in the original beam are zero, the algebraic sum of the deflections in
Fig. 47.28c, d, and e at these same points must also vanish. Thus
DD
CP CR
-=0
5
48 3
0
3
3
PL
EI
RL
EI
C
-=
R
C
=
5
16
P
R
A
=- =P
5
16
P
11
16
P
M
A
=- =
PL
2
5
16
PL
3
16
PL
© 2003 by CRC Press LLC

47-34 The Civil Engineering Handbook, Second Edition
(47.34)
It is useful in the case of complex structures to write the equations of consistent deformations in the
form
(47.35)
in which d
BC
, for example, denotes the deflection at B due to a unit load at C in the direction of R
C
.
Solution of Eq. (47.35) gives the redundant reactions R
B
and R
C
.
Example 47.5
Determine the reactions for the beam shown in Fig. 47.29, and draw its shear force and bending moment
diagrams.
It can be seen from the figure that there are three reactions viz. M
A
, R
A
, and R
C
, one more than that
required for a stable structure. The reaction R
C
can be removed to make the structure determinate. We
know that the deflection at support C of the beam is zero. One can determine the deflection d
CP
at C
due to the applied load on the cantilever in Fig. 47.29b. In the same way the deflection d
CR
at C due to
the redundant reaction on the cantilever (Fig. 47.29c) can be determined. The compatibility equation
gives
FIGURE 47.28 Beam with two redundant reactions.
(b)
ACB
A
(a)
M
A
W
1
R
A
R
C
R
B
L/2
L/2
B
C
W
2
(c)
∆
BP
∆
CP
W
1
W
2
(d)
∆
BB
∆
CB
R
B
(e)
∆
BC
∆
CC
R
C
DDD
DDD
BP BB BC
CP CB CC
--=
--=
0
0
D
D
BP BB B BC C
CP CB B CC C
RR
RR
-- =
-- =
dd
dd
0
0
© 2003 by CRC Press LLC
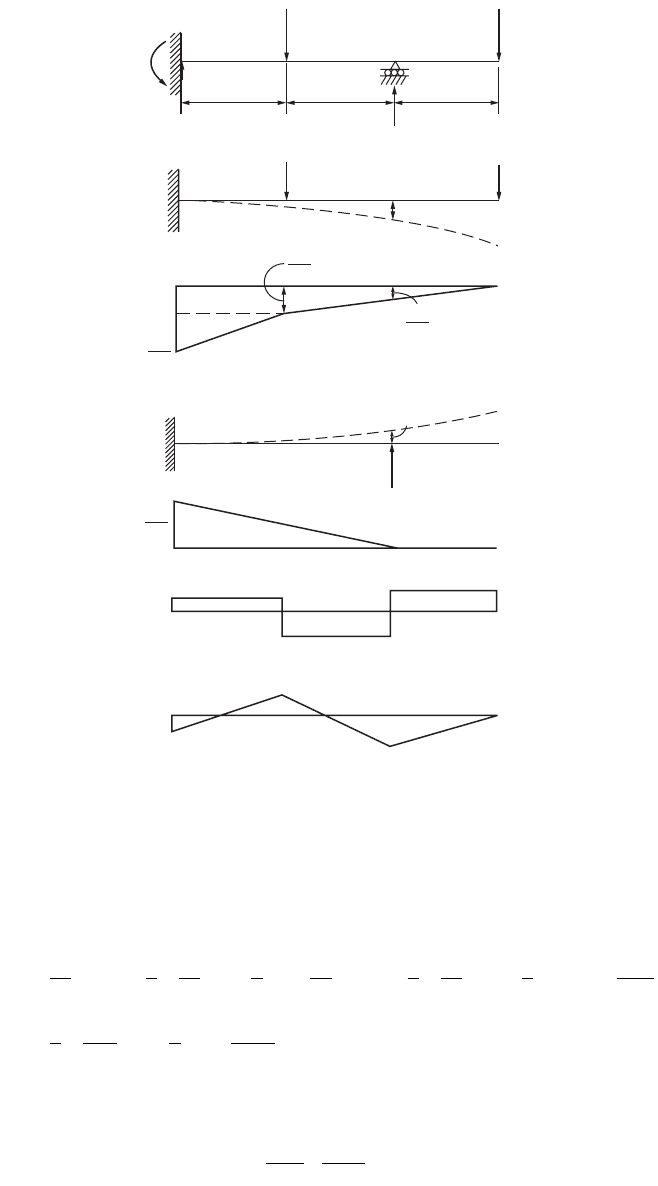
Theory and Analysis of Structures 47-35
By moment area method,
Substituting for d
CP
and d
CR
in the compatibility equation, one obtains,
FIGURE 47.29 Example 47.5.
M
A
20 kN 10 kN
R
A
2 m 2 m 2 m
EIEI
A
D
(a)
CB
20 kN
10 kN
R
C
δ
CP
(b)
40
EI
20
EI
100
EI
10 kN
6.25 kN
5 kNm
20 kNm
13.75 kN
7.5 kNm
δ
CR
R
C
(c)
(d)
4R
C
EI
+
+
+
−
−
−
dd
CP CR
-=0
d
d
CP
CR
CC
EI EI EI EI EI
R
EI
R
EI
=¥¥+¥¥¥¥+¥¥+¥¥¥¥+
Ê
Ë
Á
ˆ
¯
˜
=
=¥ ¥¥¥=
20
21
1
2
20
2
2
3
2
40
23
1
2
60
2
2
3
22
1520
3
1
2
4
4
2
3
4
64
3
1520
3EI 3EI
0-=
64R
C
© 2003 by CRC Press LLC
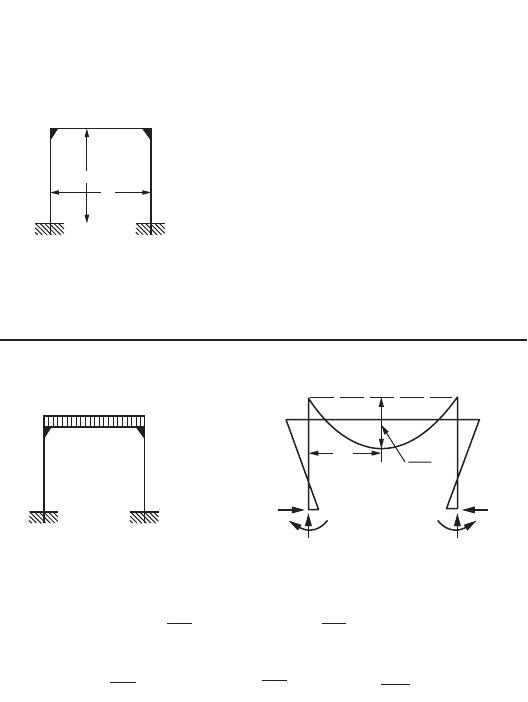
47-36 The Civil Engineering Handbook, Second Edition
from which
R
C
= 23.75 kN≠
By using statical equilibrium equations we get
R
A
= 6.25 kN≠
and M
A
= 5 kNm.
The shear force and bending moment diagrams are shown in Fig. 47.29d.
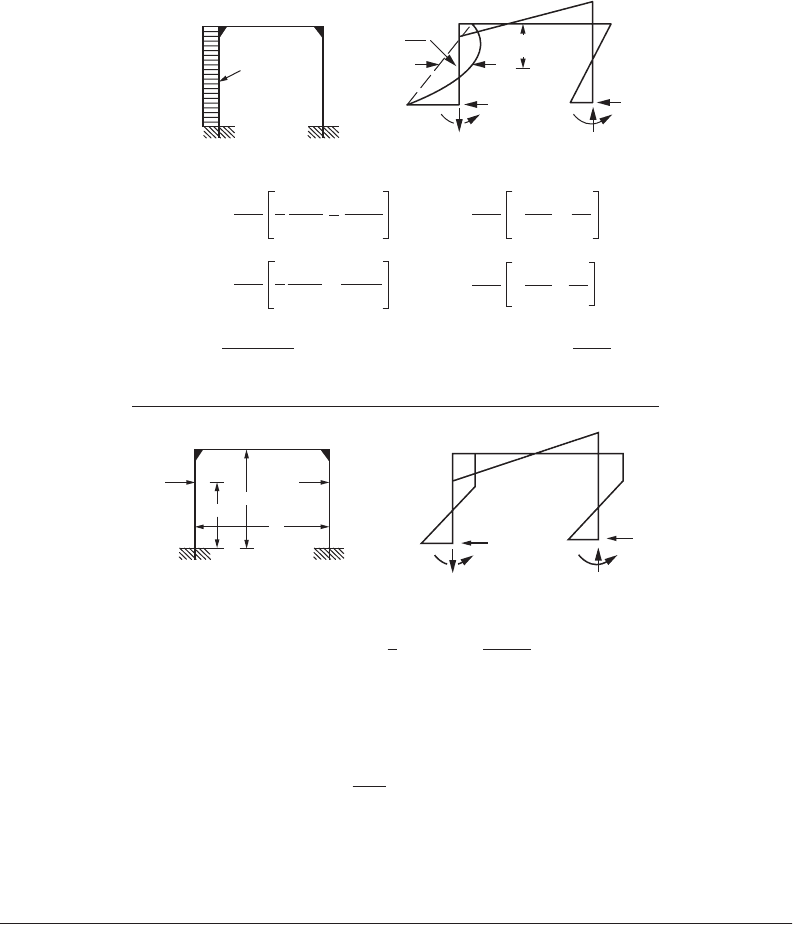
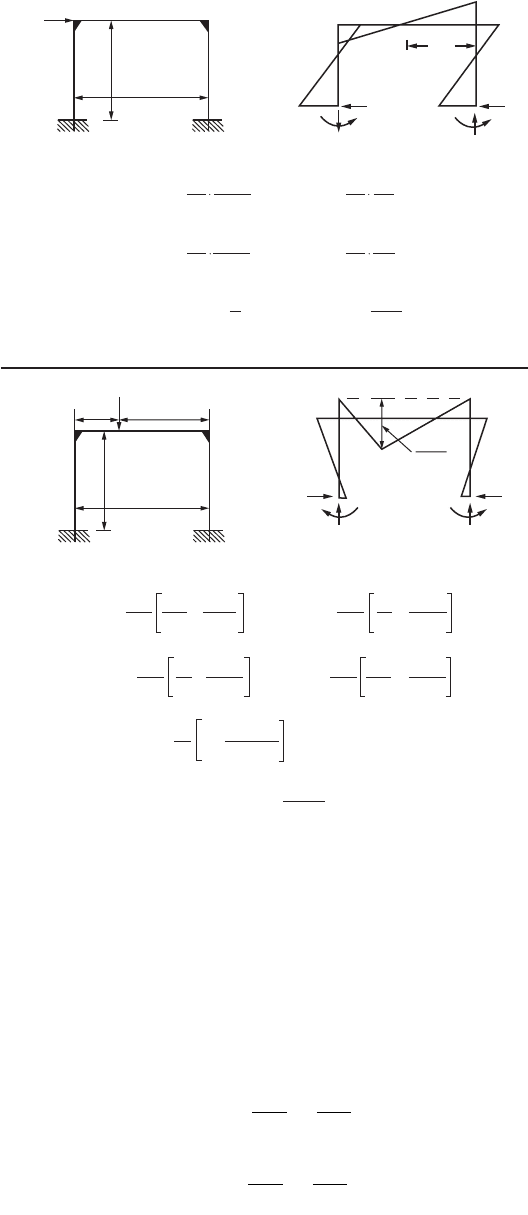
1. Solutions to fix-based portal frames subjected to various loading: Fig. 47.30 shows the bending
moment diagram and reaction forces of fix-based portal frames subjected to loading typically
encountered in practice. Closed-form solutions are provided for moments and end forces to
facilitate a quick solution to the simple frame problem.
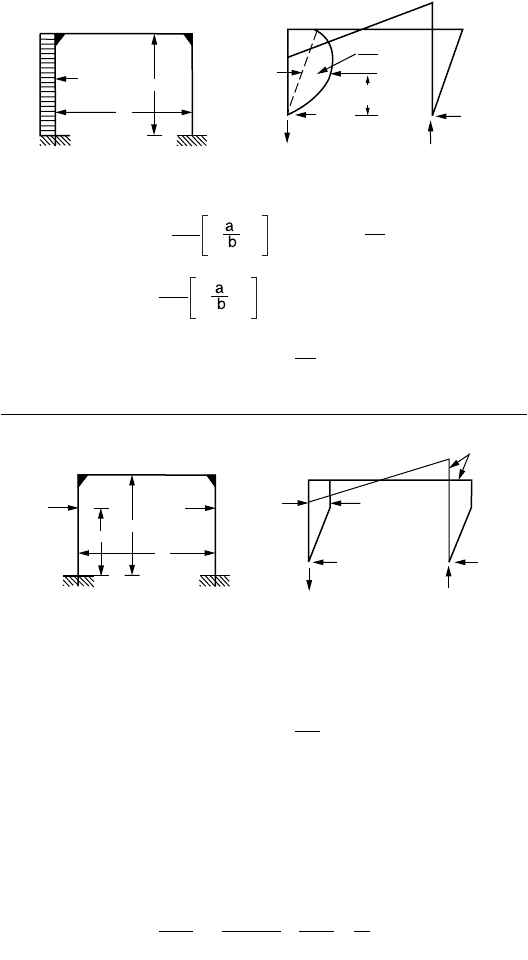
2. Solutions to pin-based portal frames subjected to various loading: Fig. 47.31 shows the bending
moment diagram and reaction forces of pin-based portal frames subjected to loading typically
encountered in practice. Closed-form solutions are provided for moments and end forces to
facilitate a quick solution to the simple frame problem.
FIGURE 47.30 Rigid frames with fixed supports.
BC
Coefficients:
FRAME DATA
h
D
A
L
I
c
I
c
a
=
(
I
b
/
L
)/(
I
c
/
h
)
b
1
=
a +
2
b
2
=
6a +
1
I
b
B
w per unit length
C
D
A
+
H
A
L
−
2
M
A
H
D
M
D
V
A
V
D
A
B
+
−−
−−
D
C
+
8
wL
2
V
A
=
V
D
=
wL
2
H
A
=
H
D
=
3
M
A
h
M
max
=
+
M
B
wL
2
8
M
A
=
M
D
=
1
w
2
L
b
2
1
M
B
=
M
C
=
−
w
6
L
b
2
1
=
- 2
M
A
Frame I
© 2003 by CRC Press LLC
Theory and Analysis of Structures 47-37
47.5 Plates
Bending of Thin Plates
A plate in which its thickness is small compared to the other dimensions is called a thin plate. The plane
parallel to the faces of the plate and bisecting the thickness of the plate, in the undeformed state, is called
the middle plane of the plate. When the deflection of the middle plane is small compared with the
thickness, h, it can be assumed that
1. There is no deformation in the middle plane.
2. The normals of the middle plane before bending are deformed into the normals of the middle
plane after bending.
3. The normal stresses in the direction transverse to the plate can be neglected.
FIGURE 47.30 (continued).
h
a
L
BC
B
B
A
D
A
+
+
+
+
+
+
D
C
h/
2
w per unit
height
DA
M
A
=
V
D
V
D
V
A
V
D
H
A
H
L
M
A
M
D
−
−
−
-
-
-
8
wh
2
wh
2
a + 3
6b
1
b
2
4a + 1
4
BC
C
P
P
DA
M
D
=
wh
2
H
D
=
H
A
=
- (
wh
-
H
D
)
wh
(2a + 3)
a + 3
6b
1
8b
1
b
2
4
V
A
=
-
V
D
=
-
wh
2
a
a
6b
1
b
2
2a
M
B
=
wh
2
4
M
C
=
wh
2
4
a
6b
1
L
b
2
H
A
=
−
H
D
=
−
PV
A
=
−
V
D
=
−
2
X
1
L
3
Paa
1
a
b
2
b
2
2a
−
−
−
H
A
M
A
a
1
=
X
1
=
M
A
=
−
Pa
+
X
1
M
D
=
+
Pa
−
X
1
M
C
=
−
X
1
M
B
=
X
1
H
D
M
D
Constants:
a
h
4a + 1
© 2003 by CRC Press LLC
47-38 The Civil Engineering Handbook, Second Edition
Based on these assumptions, all stress components can be expressed by deflection w of the plate. w is
a function of the two coordinates (x, y) in the plane of the plate. This function has to satisfy a linear
partial differential equation, which, together with the boundary conditions, completely defines w.
Figure 47.32a shows a plate element cut from a plate whose middle plane coincides with the xy plane.
The middle plane of the plate subjected to a lateral load of intensity, q, is shown in Fig. 47.32b. It can
be shown, by considering the equilibrium of the plate element, that the stress resultants are given as
(47.36)
FIGURE 47.30 (continued).
V
A
B
L
Pab
A
D
+
+
+
+
V
D
V
A
C
BC
P
ab
DA
b
2
3a
+
1
2
M
A
=
−
Ph
M
A
=
Pab
2b
1
2
L
b
2
1
b
−
a
L
V
A
=
−
V
D
=
−
−
−
−
−
−
−
M
D
=
Pab
2b
1
2
L
b
2
2
Lh
b
1
1
b
−
a
L
-
M
B
=
−
Pab
b
1
2
L
b
2
1
+
+
V
A
=
V
D
=
P
−
V
A
H
A
=
H
D
=
Pb
L
2
b
2
1
+
a
(
b
−
a
)
L
b
-
a
L
M
C
=
−
Pab
3
Pab
b
1
2
L
b
2
1
b
−
a
L
b
2
3a
2
M
B
=
+
Ph
b
2
3a
+
1
2
M
D
=
+
Ph
b
2
3a
2
M
C
=
−
Ph
−
−
H
A
H
D
M
A
M
A
H
D
H
A
M
D
V
D
M
D
B
P
C
C
B
A
D
DA
L
/2
2
M
B
L
H
A
=
−
H
D
=
−
2
P
M
X
=-
∂
∂
+
∂
∂
Ê
Ë
Á
ˆ
¯
˜
=-
∂
∂
+
∂
∂
Ê
Ë
Á
ˆ
¯
˜
D
w
x
w
y
M
D
w
y
w
x
2
2
2
2
y
2
2
2
2
n
n
© 2003 by CRC Press LLC

Theory and Analysis of Structures 47-39
(47.37)
(47.38)
(47.39)
(47.40)
where M
x
and M
y
= the bending moments per unit length in the x and y directions, respectively
M
xy
and M
yx
= the twisting moments per unit length
Q
x
and Q
y
= the shearing forces per unit length in the x and y directions, respectively
V
x
and V
y
=are the supplementary shear forces in the x and y directions, respectively
R = the corner force
D = Eh
3
/12(1 – n
2
), the flexural rigidity of the plate per unit length
E = the modulus of elasticity; and n is Poisson’s ratio
FIGURE 47.31 Rigid frames with pinned supports.
h
L
BC
I
1
I
1
I
2
DA
FRAME DATA
Coefficients:
α = (I
b
/L)/(I
c
/h)
β = 2α + 3
B
w per unit length
C
DA
+
H
A
V
A
A
B
L/
2
C
D
−
−
−
−
8
wL
2
V
A
=
V
D
=
wL
2
H
A
=
H
D
=
−
M
B
h
M
B
=
M
C
=
−
wL
2
4b
M
max
=
+
M
B
wL
2
8
H
D
V
D
xy yx
2
MM
D1
w
xy
=- = -
()
∂
∂∂
n
V
y
=
∂
∂
+-
()
∂
∂∂
3
3
3
2
w
y
w
y
x
2 n
V
x
=
∂
∂
+-
()
∂
∂∂
3
3
3
2
w
x
w
x
y
2 n
QD
y
=-
∂
∂
∂
∂
+
∂
∂
Ê
Ë
Á
ˆ
¯
˜
y
w
x
w
y
2
2
2
2
R2D1
w
xy
2
=-
()
∂
∂∂
n
© 2003 by CRC Press LLC
47-40 The Civil Engineering Handbook, Second Edition
The governing equation for the plate is obtained as
(47.41)
Any plate problem should satisfy the governing Eq. (47.41) and boundary conditions of the plate.
Boundary Conditions
There are three basic boundary conditions for plates. These are the clamped edge, simply supported edge,
and free edge.
Clamped Edge
For this boundary condition, the edge is restrained such that the deflection and slope are zero along the
edge. If we consider the edge x = a to be clamped, we have
FIGURE 47.31 (continued).
w per unit
height
B
C
h
h
/2
D
L
A
B
A
D
C
H
A
V
A
V
D
H
D
wh
2
+
+
−
−
P
B
C
P
L
D
A
a
h
B
C
−
−
+
A
V
A
V
D
H
D
H
A
D
Pa
Pa
H
D
=
−
M
h
C
H
A
=
−(
wh
−
H
D
)
V
A
=
−
V
D
=
−
w
2
h
L
2
M
B
=
−
M
c
=
Pa
H
A
=
H
d
=
P
V
A
=
−
V
D
=
−
2
P
L
a
Moment at Loads = ±
Pa
M
B
=
w
4
h
2
−
2
+
1
M
C
=
w
4
h
2
−
2
−
1
8
4
4
4
2
2
4
4
w
x
2
w
x
y
w
y
q
D
∂
∂
+
∂
∂∂
+
∂
∂
=
© 2003 by CRC Press LLC
