Wai-Fah Chen.The Civil Engineering Handbook
Подождите немного. Документ загружается.

Theory and Analysis of Structures 47-41
(47.42)
Simply Supported Edge
If the edge x = a of the plate is simply supported, the deflection w along this edge must be zero. At the
same time this edge can rotate freely with respect to the edge line. This means that
(47.43)
Free Edge
If the edge x = a of the plate is entirely free, there are no bending and twisting moments and also vertical
shearing forces. This can be written in terms of w, the deflection, as
(47.44)
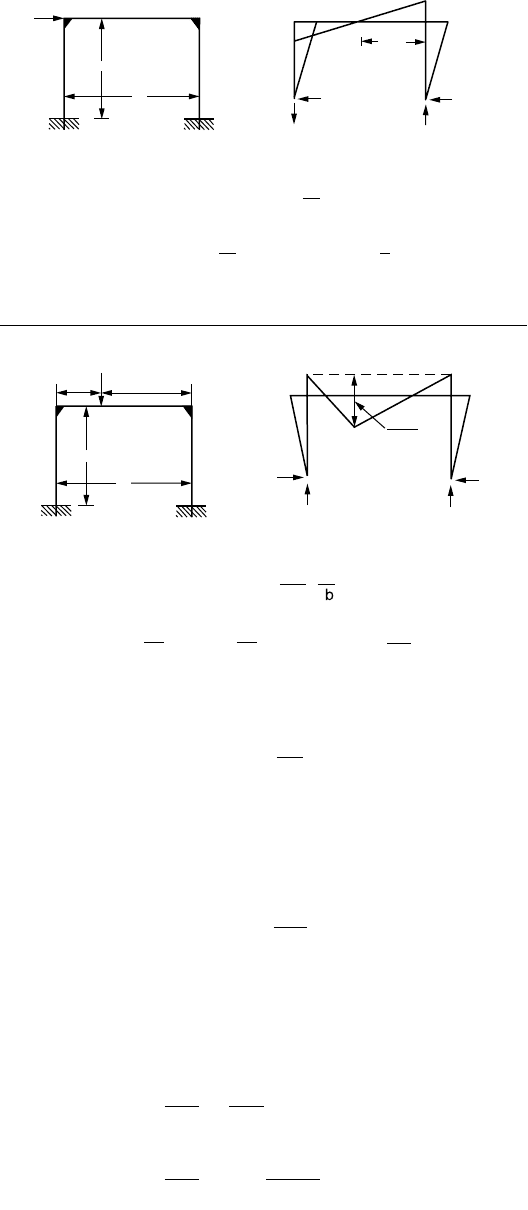
FIGURE 47.31 (continued).
P
BC
L
A
D
h
B
A
C
D
V
D
M
D
H
A
V
A
L/
2
+
a
P
b
C
B
L
D
A
h
H
A
V
D
H
D
D
C
V
A
A
B
Pa
L
b
−
−
−
−
M
B
=
−
M
C
=
+
P
2
h
V
A
=
−
V
D
=
−
P
L
h
H
A
=
−
H
D
=
−
P
2
M
B
=
M
c
=
−
P
L
ab
.
2
3
V
A
=
P
L
b
V
D
=
P
L
a
H
A
=
H
D
=
−
M
h
B
−
−
w
w
x
xa
xa
()
=
∂
∂
Ê
Ë
Á
ˆ
¯
˜
=
=
=
00;
w
w
x
xa
xa
()
=
∂
∂
Ê
Ë
Á
ˆ
¯
˜
=
=
=
00
2
2
;
x=a
22
2
x=a
33
2
ww
y
0
ww
x
y
0
∂
∂
+
∂
∂
Ê
Ë
Á
ˆ
¯
˜
=
∂
∂
+-
()
∂
∂∂
Ê
Ë
Á
ˆ
¯
˜
=
x
x
2
3
2
n
n
© 2003 by CRC Press LLC
47-42 The Civil Engineering Handbook, Second Edition
Bending of Rectangular Plates
The plate bending problem may be solved by referring to the differential Eq. (47.41). The solution,
however, depends on the loading and boundary conditions. Consider a simply supported plate subjected
to a sinusoidal loading, as shown in Fig. 47.33. The differential Eq. (47.41) in this case becomes
(47.45)
FIGURE 47.32 (a) Plate element. (b) Stress resultants.
FIGURE 47.33 Rectangular plate under sinusoidal loading.
M
xy
+
δM
δ
x
x
y
d
x
M
y
+
δM
δ
y
y
d
y
Q
x
+
δQ
δ
x
x
d
x
M
x
+
δM
δ
x
x
d
x
M
yx
+
δM
δ
y
yx
d
y
Q
y
+
δQ
δ
y
y
d
y
d
y
d
x
(a)
M
x
+
δM
δ
x
x
d
x
M
xy
+
δM
δ
x
xy
d
x
M
yx
+
δM
δ
y
yx
d
y
M
y
+
δM
δ
y
y
d
y
M
xy
M
x
M
y
M
yx
Q
y
Q
x
y
z
x
Q
x
+
δQ
δ
x
x
d
x
Q
y
+
δQ
δ
y
y
d
y
(b)
q
o
Sin
π
a
x
Sin
π
b
y
x
a
q
o
b
y
z
44
2
4
4
o
w
2
w
y
w
y
q
D
sin
x
a
sin
y
b
∂
∂
+
∂
∂∂
+
∂
∂
=
x
x
4
2
pp
© 2003 by CRC Press LLC

Theory and Analysis of Structures 47-43
The boundary conditions for the simply supported edges are
(47.46)
The deflection function becomes
(47.47)
which satisfies all the boundary conditions in Eq. (47.46). w
0
must be chosen to satisfy Eq. (47.45).
Substitution of Eq. (47.47) into Eq. (47.45) gives
The deflection surface for the plate can, therefore, be found as
(47.48)
Using Eqs. (47.48) and (47.36), we find expression for moments as
(47.49)
Maximum deflection and maximum bending moments that occur at the center of the plate can be written
by substituting x = a/2 and y = b/2 in Eq. (47.49) as
(47.50)
w0,
w
0 for x 0 and x a
w0,
w
y
0 for y 0 and y b
2
2
2
=
∂
∂
===
=
∂
∂
===
x
2
ww=
0
sin
x
a
sin
y
b
pp
4
2
22
0
o
1
a
1
b
w
q
D
p
+
Ê
Ë
Á
ˆ
¯
˜
=
w
q
D
1
a
1
b
sin
x
a
sin
y
b
o
4
22
=
+
Ê
Ë
Á
ˆ
¯
˜
p
pp
M
M
M
x
y
xy
=
+
Ê
Ë
Á
ˆ
¯
˜
+
Ê
Ë
Á
ˆ
¯
˜
=
+
Ê
Ë
Á
ˆ
¯
˜
+
Ê
Ë
Á
ˆ
¯
˜
=
+
Ê
Ë
Á
ˆ
¯
˜
o
2
2
22
22
o
2
2
22
22
o
2
2
22
q
1
a
1
b
1
ab
sin
x
a
sin
y
b
q
1
a
1
b
a
1
b
sin
x
a
sin
y
b
q
(1- )
1
a
1
b
ab
cos
x
a
cos
p
npp
p
npp
n
p
pp
yy
b
w
M
x
max
o
4
2
22
max
o
2
2
22
22
q
D
1
a
1
b
q
1
a
1
b
1
ab
=
+
Ê
Ë
Á
ˆ
¯
˜
()
=
+
Ê
Ë
Á
ˆ
¯
˜
+
Ê
Ë
Á
ˆ
¯
˜
p
p
n
© 2003 by CRC Press LLC
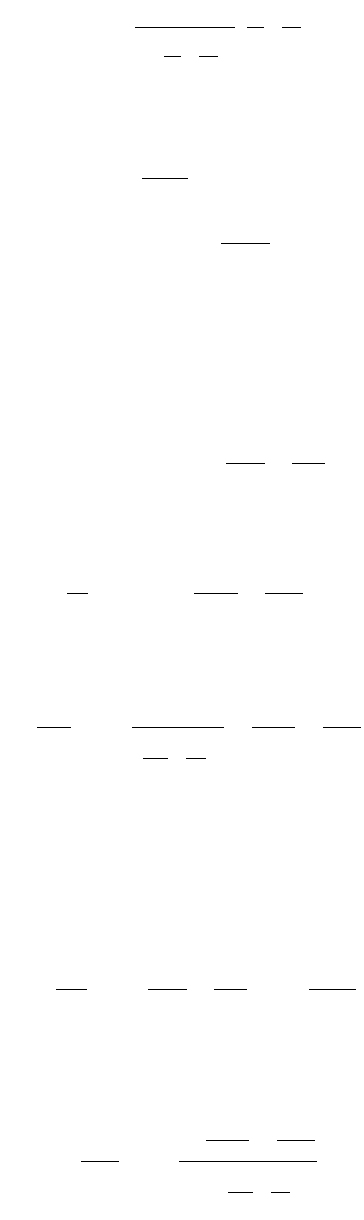
47-44 The Civil Engineering Handbook, Second Edition
If the plate is square, then a = b and Eq. (47.50) becomes
(47.51)
If the simply supported rectangular plate is subjected to any kind of loading given by
(47.52)
the function q(x, y) should be represented in the form of a double trigonometric series as
(47.53)
in which q
mn
is given by
(47.54)
From Eqs. (47.45) and (47.52) to (47.54) we can obtain the expression for deflection as
(47.55)
If the applied load is uniformly distributed of intensity q
o
, we have
and from Eq. (47.54) we obtain
(47.56)
in which m and n are odd integers. q
mn
= 0 if m or n or both are even numbers. Finally, the deflection
of a simply supported plate subjected to a uniformly distributed load can be expressed as
(47.57)
M
y
()
=
+
Ê
Ë
Á
ˆ
¯
˜
+
Ê
Ë
Á
ˆ
¯
˜
max
o
2
2
22
22
q
1
a
1
b
a
1
b
p
n
w
MM qa
xy o
max
o
4
4
max
max
q
a
4D
=
()
=
()
=
+
()
p
n
p
1
4
2
2
qqxy=
()
,
qxy q
mx
a
ny
b
mn
nm
, sin sin
()
=
=
•
=
•
ÂÂ
pp
11
mn
0
a
0
b
q
4
ab
q, sin
mx
a
sin
ny
b
dxdy=
()
ÚÚ
xy
pp
w
m
a
+
n
b
sin
mx
a
sin
ny
b
2
2
2
2
=
Ê
Ë
Á
ˆ
¯
˜
=
•
=
•
ÂÂ
1
4
2
11
p
pp
D
q
mn
nm
qxy q
o
,
()
=
q
q
ab
mx
a
ny
b
dxdy
q
mn
mn
oo
ba
==
ÚÚ
416
2
00
sin sin
pp
p
w
16
q
D
sin sin
mn
m
a
+
n
b
o
6
m=1 n=1
2
2
2
2
2
=
Ê
Ë
Á
ˆ
¯
˜
••
ÂÂ
p
ppmx
a
ny
b
© 2003 by CRC Press LLC
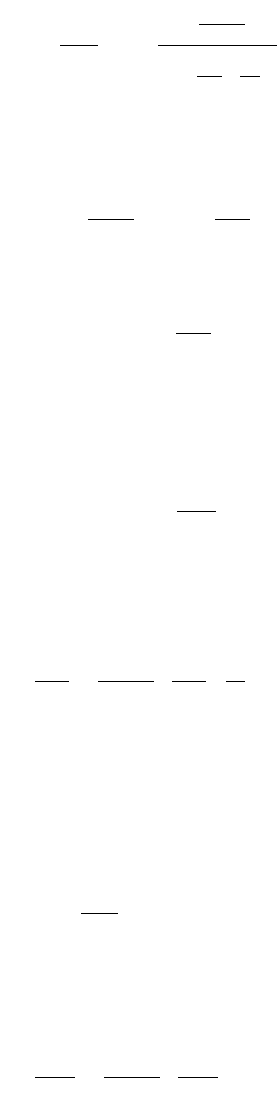
Theory and Analysis of Structures 47-45
where m = 1, 3, 5, …
n = 1, 3, 5. …
The maximum deflection occurs at the center. Its magnitude can be evaluated by substituting x = a/2
and y = b/2 in Eq. (47.57) as
(47.58)
Equation (47.58) is a rapid converging series. A satisfactory approximation can be obtained by taking
only the first term of the series; for example, in the case of a square plate,
Assuming n = 0.3, the maximum deflection can be calculated as
The expressions for bending and twisting moments can be obtained by substituting Eq. (47.57) into
Eq. (47.36). Figure 47.34 shows some loading cases and the corresponding loading functions.
If the opposite edges at x = 0 and x = a of a rectangular plate are simply supported, the solution taking
the deflection function as
(47.59)
can be adopted. Equation (47.59) satisfies the boundary conditions w = 0 and ∂
2
w/∂x
2
= 0 on the two
simply supported edges. Y
m
should be determined such that it satisfies the boundary conditions along
the edges y = +b/–2 of the plate shown in Fig. 47.35 and also the equation of the deflection surface
(47.60)
q
o
being the intensity of the uniformly distributed load.
The solution for Eq. (47.60) can be taken in the form
(47.61)
for a uniformly loaded simply supported plate. w
1
can be taken in the form
(47.62)
representing the deflection of a uniformly loaded strip parallel to the x axis. It satisfies Eq. (47.60) and
also the boundary conditions along x = 0 and x = a.
The expression w
2
has to satisfy the equation
(47.63)
w
mn
max
o
6
m=1 n=1
2
2
2
2
2
16
q
D
mn
m
a
+
n
b
=
-
()
+
-
Ê
Ë
Á
ˆ
¯
˜
••
ÂÂ
p
1
2
1
w
max
o
4
6
o
4
4
q
a
D
0.00416
q
a
D
==
p
w
max
o
4
3
0.0454
q
a
E
h
=
wY
mx
a
m
m
=
=
•
Â
sin
p
1
44
2
4
4
o
w
2
w
y
w
y
q
D
∂
∂
+
∂
∂∂
+
∂
∂
=
x
x
4
2
ww w=+
12
waxax
1
33
2=-+
()
o
4
q
24D
x
4
2
4
2
2
4
2
4
w
2
w
y
w
y
0
∂
∂
+
∂
∂∂
+
∂
∂
=
x
x
4
2
© 2003 by CRC Press LLC
47-46 The Civil Engineering Handbook, Second Edition
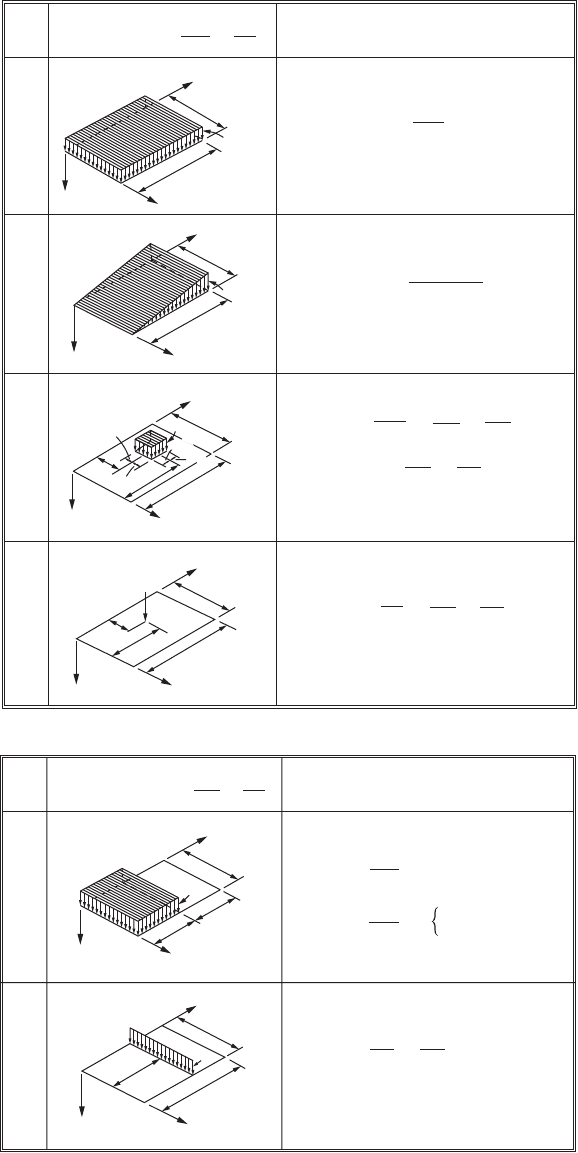
FIGURE 47.34 Typical loading on plates and loading functions.
No.
1
2
3
4
q(x,y)
=
Σ
m
Σ
n
q
mn
sin
mπ
a
x
sin
nπ
b
y
Load
Expansion Coefficients
q
mn
q
mn
=
π
1
2
6
m
q
n
o
(m,
n
=
1, 3, 5,....)
(m,
n
=
1, 3, 5,....)
(m,
n
=
1, 3, 5,....)
(m,
n
=
1, 3, 5,....)
q
mn
=
−8q
o
π
2
c
m
os
n
mπ
×
sin
m
2
π
a
c
sin
n
2
π
b
d
p
mn
=
π
1
2
6
m
q
n
o
sin
mπ
a
ξ
sin
nπ
b
η
q
mn
=
4
a
q
b
o
sin
mπ
a
ξ
sin
nπ
b
η
X
b
q
o
a
Z,w
X
b
q
o
a
Y
Y
Z,w
X
b
q
o
a
Z,w
Y
d/2
d/2
η
ξ
X
b
η
Z,w
a
ξ
P
Y
c/2
c/2
No.
q(x,y) =
Σ
m
Σ
n
q
mn
sin
mπ
a
x
sin
nπ
b
y
Load
5
6
Z,w
Z,w
Y
Y
X
X
b
b
a/2
a/2
q
o
q
o
a
ξ
Expansion Coefficients
q
mn
q
mn
=
π
2
8
m
q
n
o
for m,n
=
1, 3, 5,....
q
mn
=
π
1
2
6
m
q
n
o
for
n
=
1, 3, 5,....
m
=
2, 6, 10,....
(m,n
=
1, 2, 3, ....)
q
mn
=
π
4
a
q
n
o
sin
mπ
a
ξ
© 2003 by CRC Press LLC

Theory and Analysis of Structures 47-47
and must be chosen such that Eq. (47.61) satisfies all boundary conditions of the plate. Taking w
2
in the
form of series given in Eq. (47.59), it can be shown that the deflection surface takes the form
(47.64)
Observing that the deflection surface of the plate is symmetrical with respect to the x axis, only even
functions of y are kept in Eq. (47.64); therefore, C
m
= D
m
= 0. The deflection surface takes the form
(47.65)
Developing the expression in Eq. (47.62) into a trigonometric series, the deflection surface in Eq. (47.65)
is written as
(47.66)
Substituting Eq. (47.5.30) in the boundary conditions
(47.67)
one obtains the constants of integration A
m
and B
m
, and the expression for deflection may be written as
(47.68)
in which a
m
= mpb/2a.
Maximum deflection occurs at the middle of the plate, x = a/2, y = 0, and is given by
(47.69)
FIGURE 47.35 Rectangular plate.
a
y
x
b
/
2
b
/
2
w
q
24D
x
2
ax a
x
q
a
24D
A
cosh
my
a
B
my
a
sinh
my
a
C
sinh
my
a
D
my
a
cosh
my
a
sin
mx
a
o
433
o
4
m=1
mm
mm
=-+
()
++
Ê
Ë
Á
++
ˆ
¯
˜
•
Â
ppp
pppp
w =-+
()
++
ˆ
¯
˜
Ê
Ë
Á
•
Â
o
433
o
4
m=1
mm
q
24D
x
2
ax a
x
q
a
24D
A
cosh
my
a
B
my
a
sinh
my
a
sin
mx
a
ppp p
w =++
Ê
Ë
Á
ˆ
¯
˜
•
Â
o
4
m=1
5
5
mm
q
a
D
4
m
A
cosh
my
a
B
my
a
sin
my
a
sin
mx
a
p
pppp
w
w
y
==00
2
2
,
∂
∂
w =-
+
+
ˆ
¯
˜
Ê
Ë
Á
•
Â
4
q
a
D
1
m
1
tanh 2
2cosh
cosh
2y
b2cosh
2y
b
sinh
2y
b
sin
mx
a
o
4
5
m=1,3,5...
5
mm
m
mm
m
m
p
aa
a
aa
a
a
p
w
m
m
max
o
4
5
m=1,3,5,...
mm
m
4
q
a
D
1
tanh 2
2cosh
=
-
()
-
-
+
Ê
Ë
Á
ˆ
¯
˜
•
Â
p
aa
a
1
1
2
5
© 2003 by CRC Press LLC

47-48 The Civil Engineering Handbook, Second Edition
The solutions of plates with arbitrary boundary conditions are complicated. It is possible to make some
simplifying assumptions for plates with the same boundary conditions along two parallel edges in order
to obtain the desired solution. Alternately, the energy method can be applied more efficiently to solve
plates with complex boundary conditions. However, it should be noted that the accuracy of results
depends on the deflection function chosen. These functions must be chosen so that they satisfy at least
the kinematics boundary conditions.
Figure 47.36 gives formulas for deflection and bending moments of rectangular plates with typical
boundary and loading conditions.
FIGURE 47.36 Typical loading and boundary conditions for rectangular plates.
q
o
q
o
X
X
Z,w
0
b
a
Y
X
A
ξ
Z
q
o
0
A-A
b/2
b/2
Y
a
A
X
Small
q
o
A-A
Z,w
A
0
c
d
b
a
η
ξ
η
ξ
P
P
X
X
Z,w
Y
X
X
c/2 c/2
0
Y
a
b
1
2
3
4
Case
No.
Structural System and Static
Loading
Deflection and Internal Forces
m = 1,2,3,...
n = 1,2,3,...
w =
1
π
6
6
q
D
o
Σ
m
Σ
n
sin
mπ
a
x
sin
nπ
b
y
mn
m
a
2
2
+
n
b
2
2
2
n = 1, 3, 5,...., ∞
=
b
a
,
m = 1, 3, 5,....,∞;
m
y
=
16.
π
q
4
o
a
2
Σ
m
Σ
n
n
2
2
+ vm
2
sin
mπ
a
x
sin
nπ
b
y
mn
m
2
+
n
2
2
2
m
2
+ ν
n
2
2
sin
mπ
a
x
sin
nπ
b
y
mn
m
2
+
n
2
2
2
m
x
=
16q
π
ο
4
a
2
Σ
m
Σ
n
w =
Dπ
4P
4
ab
Σ
m
Σ
n
sin
mπ
a
ξ
sin
nπ
b
η
sin
mπ
a
x
sin
nπ
b
y
m
a
2
2
+
n
b
2
2
2
m = 1, 2, 3,...
n = 1, 2, 3,...
× sin
mπ
a
x
sin
nπ
b
y
w =
1
D
6
π
q
6
o
Σ
m
Σ
n
sin
mπ
a
ξ
sin
nπ
b
η
sin
mπ
a
c
sin
nπ
2b
d
mn
m
a
2
2
+
n
b
2
2
2
where
P
m
=
2q
a
o
sin
mπ
a
ξ
λ
m
=
m
a
π
α
m
=
m
2
π
a
b
m
=
1, 2, 3,...
+
λ
m
2
y
c
s
o
i
s
n
h
h
α
λ
m
m
y
sinλ
m
x
w =
D
a
π
4
4
m=1
P
m
m
4
1 −
2
+
2
α
c
m
os
ta
h
n
α
h
m
α
m
cosλ
m
y
∞
∋
∋
∋
∋
Σ
© 2003 by CRC Press LLC

Theory and Analysis of Structures 47-49
Bending of Circular Plates
In the case of a symmetrically loaded circular plate, the loading is distributed symmetrically about the
axis perpendicular to the plate through its center. In such cases, the deflection surface to which the middle
plane of the plate is bent will also be symmetrical. The solution of circular plates can be conveniently
carried out by using polar coordinates.
Stress resultants in a circular plate element are shown in Fig. 47.37. The governing differential equation
is expressed in polar coordinates as
(47.70)
in which q is the intensity of loading.
In the case of a uniformly loaded circular plate, Eq. (47.70) can be integrated successively and the
deflection at any point at a distance r from the center can be expressed as
(47.71)
in which q
o
is the intensity of loading and a is the radius of the plate. C
1
, C
2
, and C
3
are constants of
integration to be determined using the boundary conditions.
FIGURE 47.37 (a) Circular plate. (b) Stress resultants.
Y
ϕ
X
r
y
x
0
r
o
Middle surface
p
z
dr rd
ϕ
r
m
ϕr
q
ϕ
m
ϕ
d
ϕ
dr
q
r
m
r
0
r′,ϕ=0
m
rϕ
Z,w(r,ϕ)
h/2
h/2
m
r
+
δm
δr
r
dr
m
rϕ
+
δm
δr
rϕ
dr
m
ϕ
+
δm
δ
ϕ
ϕ
d
ϕ
q
r
+
δ
δ
q
r
r
dr
ϕ
m
ϕr
+
δm
δ
ϕ
ϕr
d
ϕ
q
ϕ
+
δq
δ
ϕ
ϕ
d
ϕ
1
r
d
dr
r
d
dr
1
r
d
dr
r
dw
dr
q
D
Ê
Ë
Á
ˆ
¯
˜
È
Î
Í
˘
˚
˙
Ï
Ì
Ó
Ô
¸
˝
˛
Ô
=
w
q
r
64D
Cr
4
C
log
r
a
C
o
4
1
2
23
=++ +
© 2003 by CRC Press LLC
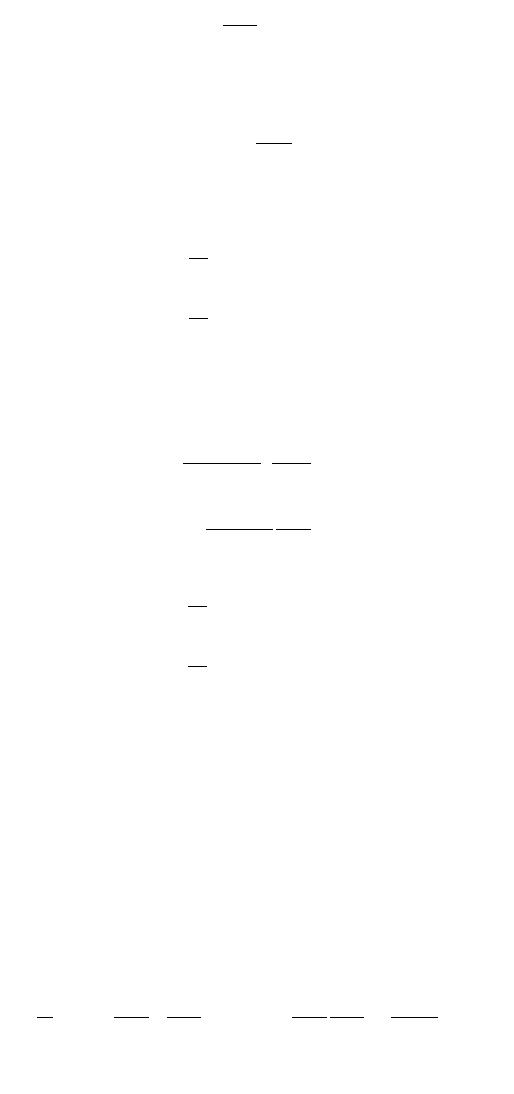
47-50 The Civil Engineering Handbook, Second Edition
For a plate with clamped edges under uniformly distributed load q
o
, the deflection surface reduces to
(47.72)
The maximum deflection occurs at the center, where r = 0, and is given by
(47.73)
Bending moments in the radial and tangential directions are respectively given by
(47.74)
The method of superposition can be applied in calculating the deflections for circular plates with
simply supported edges. The expressions for deflection and bending moment are given as
(47.75)
(47.76)
This solution can be used to deal with plates with a circular hole at the center and subjected to concentric
moment and shearing forces. Plates subjected to concentric loading and concentrated loading also can
be solved by this method. More rigorous solutions are available to deal with irregular loading on circular
plates. Once again, the energy method can be employed advantageously to solve circular plate problems.
Figure 47.38 gives deflection and bending moment expressions for typical cases of loading and boundary
conditions on circular plates.
Strain Energy of Simple Plates
The strain energy expression for a simple rectangular plate is given by
(47.77)
A suitable deflection function w(x, y) satisfying the boundary conditions of the given plate may be chosen.
The strain energy, U, and the work done by the given load, q(x, y),
w
q
D
ar
o
=-
64
222
()
w
q
a
64D
o
4
=
M
M
r
t
=+
()
-+
()
[]
=+
()
-+
()
[]
o
22
o
22
q
16
a
1
r
3
q
16
a
1
r
13
nn
nn
w
q
ar
64D
5
1
ar
5
64 1
q
a
D
o
22
22
max
o
4
=
-
()
+
+
-
Ê
Ë
Á
ˆ
¯
˜
=
+
+
()
n
n
n
n
w
M
M
r
t
=+
()
-
()
=+
()
-+
()
[]
o
22
o
22
q
16
3
ar
q
16
a
3
r
13
n
nn
U
D
2
w
x
w
y
21
w
x
w
y
w
xy
dxdy
2
2
2
2
2
2
2
2
2
2
2
=
∂
∂
+
∂
∂
Ê
Ë
Á
ˆ
¯
˜
--
()
∂
∂
∂
∂
-
∂
∂∂
Ê
Ë
Á
ˆ
¯
˜
È
Î
Í
Í
˘
˚
˙
˙
¸
˝
Ô
˛
Ô
Ï
Ì
Ô
Ó
Ô
ÚÚ
n
area
© 2003 by CRC Press LLC
