Zuo-Guang. Ye Advanced Dielectric Piezoelectric and Ferroelectric Materials: Synthesis, Characterisation and Applications

Подождите немного. Документ загружается.

Handbook of dielectric, piezoelectric and ferroelectric materials640

It has been revealed experimentally that the same domain shapes can be

obtained in a wide range of applied fields and the switching times, so the

ratio V

gen

demonstrates non-trivial dependence on the experimental

conditions. According to my general approach the V

gen

ratio is determined

by the screening efficiency, because the role of the residual depolarization

fields increases for ineffective screening.

For incomplete screening the residual depolarization field hampers the

step generation and growth processes. It can be shown that the influence of

the train of uncompensated depolarization field is more pronounced for the

step growth (1D nucleation) along the sides of a polygon as compared with

the step generation (2D nucleation) at the vertices. Thus, under non-equilibrium

conditions (for R >> 1) V

gen

can essentially exceed V

leading to increase of

the step concentration at the wall, which determines the deviation of the wall

orientation from Y directions. Formation of the regular hexagonal domain

shape in LN can be observed only for the equilibrium switching conditions

(for R << 1) with complete screening, when the step concentration is negligible

and the angles at the ‘growing vertices’ are close to 120°. The increase of R

within this approach must lead to increase of the step concentration and to

decrease of the angles at the ‘growing vertices’. In this case the ‘vicinal

walls’ formed essentially deviate from the Y directions imposed by crystal

symmetry.

Based on the above-presented considerations we can state that the shape

of individual domains is determined by domain kinetics which depends on

the switching conditions. The convincing experimental proof of this statement

is presented in Fig. 21.7, demonstrating that it is possible to produce domains

with qualitatively different shapes in the same place on the CLN wafer. The

5µm

21.7

The shapes of domains formed by switching and spontaneous

backswitching in CLN. Switching by short pulse with abrupt edge.

Optical images of domains revealed by etching.

WPNL2204

Nano- and micro-domain engineering 641

domain structure has been produced in single-domain CLN by application of

short rectangular unipolar field pulse with abrupt edge. In this case the new

domains appear within the already switched area as a result of backswitching

after the external field has been switched off (Fig. 21.1e).

The domain structure was revealed by selective chemical etching. The

dark curves on the image correspond to the position of the domain walls. The

large hexagon domain was formed during application of the pulse. The

subsequent backswitching after field switch off leads to formation of triangular

domain in the center of the switched one. The usage of abrupt pulse edge

allows the non-equilibrium conditions for backswitching to be realized.

21.5.2 Domain shape evolution during merging

The domain shape evolution after merging of hexagonal domains was studied

by in situ observation. The most interesting result is the formation of the

strictly oriented X wall after merging of two Y oriented domain walls (Fig.

21.8). The velocity of X wall motion far exceeds the velocity of Y walls. As

a result, the ‘super-mobile’ X wall disappears quickly. The limited lifetime

hinders the direct observation of X wall in the course of the switching

process in the constant field. Nevertheless, switching off the external field

allows the unusual domain polygons with both Y and X walls to be fixed.

According to the above-discussed general approach, the sideways wall

motion velocity is determined by generation rate of the elementary steps.

The abnormally high velocity of the X wall is caused by the maximum

possible density of the elementary steps remaining constant throughout the

lifetime (Fig. 21.8a). The X wall motion velocity is determined by the growth

velocity of elementary steps which reaches meters per second. It is about

1000 times faster than the average sideways Y wall motion velocity in the

same switching conditions. The computer simulation of the domain shape

(a)

(b)

(c)

(d)

(e)

21.8

Schematic drawing of domain shape evolution as a result of

domain merging; (a) formation of

wall, (b) two (

) hexagons

before merging, (c) concave (

) shape, (d) convex (

) shape,

(e) convex (

) shape.

WPNL2204

Handbook of dielectric, piezoelectric and ferroelectric materials642

evolution after merging based on the step growth mechanism allowed all

experimentally observed ‘abnormal’ convex polygonal domains with side

numbers ranging from 6 to 12 to be obtained.

The complete evolution of the domain shapes as a result of merging of

two hexagonal domains with Y walls only ((Y)

convex

) (Fig. 21.8b) can be

presented by the following scheme:

(Y)

convex

+ (Y)

convex

→ (Y + X)

concave

→ (Y + X)

convex

→ (Y)

convex

21.7

The concave domain shape (Y + X)

concave

appears just after the merging of

two convex ones (Fig. 21.8c). Such an unusual temporary shape transforms

in a short time to the convex one (Y + X)

convex

due to the fast motion of the

X wall (Fig. 21.8d). At the concave domain stage the length of the X wall

increases. Just after formation of convex domain, the length of the X wall

starts to decrease and then disappears, thus forming the hexagonal domain

with Y walls only (Fig. 21.8e).

The evolution during merging of the regular 2D domain structure produced

by the hexagonal grid electrode pattern has been studied systematically. The

merging of individual domains has been stimulated by artificial conducting

defects between neighboring electrodes. The domain evolution after merging

has been studied in detail both experimentally and by computer simulation

(Fig. 21.9). It has been shown that the shapes of the domain polygons appeared

at different stages of shape evolution are determined by the number and

succession of merging events. The abrupt switching off of the applied field

allows any intermediate domain shape to be stabilized. For example, the

simultaneous merging of three hexagon domains leads to formation of the

regular nonagon (Fig. 21.9a), while consecutive merging of the same domains

results in formation of an octagon (Fig. 21.9b). The understanding of the

origin of abnormal polygon domain shapes can be used to create desirable

domain shapes choosing the proper electrode pattern.

21.5.3 Loss of the domain wall shape stability

The various effects of loss of the domain wall shape stability are observed

for R >> 1, when switching is realized under highly non-equilibrium conditions.

The loss of stability in this case is caused by self-assembled nucleation and

oriented growth of domain rays. The typical finger and dendrite structures

formed due to wall shape instability in LN are presented in Fig. 21.10.

The non-equilibrium switching can be realized experimentally under

different conditions. There are two ways to increase the role of the screening

retardation effect. The first is to accelerate the polarization reversal process

by application of a ‘super-strong’ external field.

WPNL2204

Nano- and micro-domain engineering 643

The second is to increase the input of residual depolarization field by

deposition of the artificial surface dielectric layer. This layer effectively

increases the thickness of the dielectric gap, thus increasing the value of the

residual depolarization field remaining after completion of the fast external

screening. This residual field hampers the motion of the domain wall as a

whole.

This situation is realized during the conventional method of production of

the tailored domain structures in LN and LT by application of electric field

using periodical electrode pattern (Yamada et al., 1993; Webjörn et al.,

1994; Zhu et al., 1995; Myers et al., 1995; Batchko et al., 1999; Rozenman

et al., 1999). The area between the stripe electrodes is covered by photoresist

and domain ‘broadening’ out of the electrodes is frequently accompanied by

the loss of the regular wall shape (Shur, 2005, 2006). Various instabilities of

the domain shape leading to formation of ‘fingers’ (Fig. 21.10a), ‘branches’

and ‘dendrites’ (Fig. 21.10b) were revealed (Shur, 2005, 2006). It must be

stressed that all these self-assembled structures are formed as a result of

(a)

(b)

(c)

(d)

5µm

21.9

Experimental (right) and simulated (left) domain polygons with

and

walls formed as a result of merging of three regular

hexagon domains: (a) nonagon and (b) octagon. Optical images of

domains revealed by etching.

WPNL2204

Handbook of dielectric, piezoelectric and ferroelectric materials644

growth in strictly oriented directions. Such behavior is in accord with the

above-discussed approach.

The uncompensated depolarization field suppresses the broadening of the

strip domains by the sideways motion out of electrodes. Nevertheless, the

alternative mechanism of the broadening through formation of ‘fingers’ can

be observed. The individual finger is a ray oriented along the Y direction,

which has been generated by perturbation at the domain wall. The regular

distribution of the fingers is caused by the electrostatic interaction between

the neighbors.

21.5.4 Dendrite domain structures

The non-equilibrium switching is easily achieved during spontaneous

polarization reversal after abrupt switching off of the external electric field

(backswitching). In this case the retardation of the screening leads to the

existence of strong switching field produced by an uncompensated

depolarization field. The fast backward motion of the wall as a whole terminates

after a small backward shift under the action of appearing residual

depolarization field (Shur, 2005, 2006).

The alternative scenario of the backward wall motion is realized through

the formation and propagation of the quasi-regular structure of fingers strictly

oriented along allowed Y directions, which differ for different sides of the

stripe domain. These two finger structures grow towards each other, but the

electrostatic interaction between approaching fingers prevents their merging

(Shur, 2005). The same effect prevents merging of the neighboring fingers.

As a result, the ‘dendrite-like’ stable structure of residual domains remains

at the end of backswitching (Fig. 21.10b). The complicated shape of individual

fingers is caused by branching. It is seen from detailed analysis of the images

that the branches are also oriented only along allowed Y directions. The

(a)

(b)

5µm5µm

21.10

(a) Finger domain structure formed during periodical poling in

CLN. (b) Dendrite structure formed during backswitching in MgO:LN.

+ view. Black lines show the position of stripe electrode. Optical

images of domains revealed by etching.

WPNL2204

Nano- and micro-domain engineering 645

higher mobility of the front of finger structure as compared with the plane

domain wall is due to the diminishing of the deceleration effect for quasi-

periodic distribution of bound charges (Fatuzzo and Merz, 1967; Lines and

Glass, 1977).

21.6 Self-assembled nanoscale domain structures

The rapid development of the new SPM methods with nanoscale resolution

for visualization of the domain patterns has revolutionized our conception of

the domain kinetics in the case of ineffective screening. A recent study (Shur

et al., 2000a) reveals that along with continuous domain growth (growth of

fingers and dendrites) the discrete switching through the formation of structures

consisting of isolated nanoscale domains can be observed during polarization

reversal at the highly non-equilibrium conditions (R >> 1) (Fig. 21.11). It

has been shown experimentally that the discrete switching through formation

and enlargement of the ensemble of nano-domains occurs in LN. The self-

assembled structures usually demonstrate quasi-regular spatial distribution

of the monomers (isolated nano-domains).

We have discovered the effect of self-maintained spontaneous decay of

the stripe domain structure in CLN through arising and growth of the oriented

nanoscale domain arrays (Batchko et al., 1999; Shur et al., 2000a, 2001,

2003). The domain patterns, revealed by etching and visualized by AFM

(Fig. 21.11a) and SEM (Fig. 21.11b), demonstrate the array-assisted reversal

motion of the existing domain walls through propagation of the highly organized

quasi-periodical structure of domain arrays strictly oriented along

crystallographic directions. Each quasi-regular array is comprised of nano-

domains with a diameter 30–100nm and an average linear density exceeding

(b)

1µm

(a)

1400

µm

21.11

Stable nano-domain arrays in CLN formed as a result of

backswitching during periodical poling. Black rectangles – electrode

position.

+ view. Domain patterns revealed by etching and

visualized by (a) AFM and (b) SEM.

WPNL2204

Handbook of dielectric, piezoelectric and ferroelectric materials646

–1

. Such a domain evolution scenario was observed during switching

using periodical stripe electrodes oriented along the Y-direction deposited on

the Z+-surface. It has been shown that for a sufficient domain spreading out

of the electrodes (obtained for short switching pulse duration ∆t

~ 5ms and

a small field-diminishing amplitude ∆E ~ 2kV/mm) the backswitched domain

evolution represents self-maintained, self-organized growth of oriented

nanoscale domain arrays.

The typical structure produced in CLN covered by artificial dielectric

layer (photoresist) as a result of backswitching after the electric field switch-

off is shown in Fig. 21.10. This domain pattern is stable (frozen-in) and does

not undergo any evident changes for years. According to the optical visualization

with low spatial resolution this structure consists of fingers strictly oriented

along three crystallographic directions similar to the dendrite structures. But

the detailed visualization of these stable domain patterns by SPM reveals

that in this case each finger is an array of nanoscale monomers (Fig. 21.11).

The statistical analysis of the monomer distribution along the array reveals

that the distances between the neighboring monomers are highly correlated.

The effect of correlated nucleation was studied also during switching in

uniform electric field in CLN with surface layer modified by proton exchange.

The in situ recording of the set of instantaneous domain patterns reveals that

the stripe area filled by isolated nanoscale domains propagates in front of the

moving domain wall (Fig. 21.12). The domain growth in this case is achieved

through the appearance of new chains of individual nano-domains in front of

the stripe, while the trailing edge of the stripe is swept by the wall of the

growing solid domain (Shur et al., 2006). It is necessary to point out that in

this experiment the non-equilibrium switching conditions (R >> 1) are fulfilled

100µm

21.12

Propagation of the stripe area filled by isolated nano-scale

domains in front of the moving domain wall during switching in CLN

with proton-exchanged surface layer. Instantaneous optical image.

WPNL2204

Nano- and micro-domain engineering 647

as the proton exchange leads to the formation of the thick surface dielectric

layer (Shur et al., 2004b).

Another clear demonstration of correlated nucleation effect was observed

for switching in a uniform electric field in SLT completely covered by a

thick artificial dielectric layer (2 µm-thick photoresist) using liquid electrodes

(Shur et al., 2002b; Shur, 2005, 2006). In these conditions the web-like self-

assembled domain structures appear around the pinholes in the dielectric

layer (Fig. 21.13).

The switching process starts as the formation of a ‘hexagon’ domain

around the pinhole. The visualization of the structure by optical microscope

reveals that its subsequent growth is achieved through propagation of the

quasi-regular ensemble of microscale isolated domains. It is possible to

obtain the information about the domain structure evolution by analysis of

the static domain pattern as the positions of the domain chains can be attributed

to the subsequent locations of the ensemble boundary. Such analysis allows

us to conclude that the growth of this structure (evolution of the ensemble

(a)

(c)

15µm

(b)

(d)

Frequency

0.3

0.2

0.1

0.0

0.5 1.0 1.5 2.0 2.5

Distance (µm)

21.13

Web-like self-assembled domain structures formed in SLT

covered by photoresist. (a), (c) Optical images of structures revealed

by etching. (b) Boundary of ensemble of microscale isolated

domains. (d) Distributions function of the distances between the

neighboring domains.

WPNL2204

Handbook of dielectric, piezoelectric and ferroelectric materials648

boundary) follows the same rules as the continuous growth of the isolated

domain. For discrete switching the ensemble boundary shown in

Fig. 21.13b plays the role of the domain wall. The shape of the switched area

is the same regular polygon as in the case of isolated domain growth (see

Section 21.5). The boundaries are oriented in strict crystallographic directions.

One can observe the formation of the steps and their propagation along the

boundary.

The spatial correlation of the individual domain distribution is clearly

demonstrated by statistical analysis of the distances between the neighboring

domains (Fig. 21.13d). The obtained averaged distance between domains is

very close to the thickness of the artificial dielectric gap. This fact opens the

possibility of evaluating the effective depth of the intrinsic dielectric layer

for any material and any experimental condition by measuring the average

period of the quasi-regular structure appearing during discrete switching for

R >> 1.

All the above-discussed self-assembled structures are formed as a result

of correlated nucleation in the vicinity of the moving domain wall or the

propagating boundary of the enlarging domain ensemble. The effect is caused

by the influence on the nucleation probability of the trail of the uncompensated

depolarization field behind the moving wall or propagating boundary. To

explain the effect we have calculated the spatial distribution of the electric

field in the vicinity of the domain wall with the trail in the ferroelectric

capacitor (plate covered by uniform electrodes) with the surface dielectric

layers. It has been shown that the distribution of the field value at the boundary

between the ferroelectric and dielectric layer demonstrates a pronounced

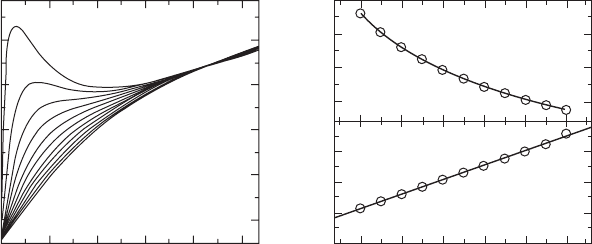
maximum at some distance from the wall (Fig. 21.14a). This distance is

about the thickness of the surface dielectric layer L.

While the field maximum diminishes with the depth (Fig. 21.14),

nevertheless the existence of the field maximum drastically changes the

domain kinetics. On one hand, the trail of uncompensated depolarization

field suppresses the nucleation at the wall, thus terminating the classical wall

motion. On the other hand, it induces the field maximum, which increases

the probability of nucleation at the definite distance in front of the wall. The

growth of nuclei leads to the appearance along the wall of the isolated

needle-like micro-domains with charged walls. The sideways growth of any

isolated domains that arise is suppressed due to the same effect of the

uncompensated depolarization field. The decrease of the local electric field

in the vicinity of each isolated domain initiates the formation of new domains

at some distance from each other. As a result, the quasi-regular domain chain

aligns along the wall.

It has been calculated that the new field maximum appears at the distance

from the formed domain chain thus initiating formation of the new chain,

leading to self-maintained enlarging of the domain ensemble. It has been

WPNL2204

Nano- and micro-domain engineering 649

shown experimentally that these self-assembled structures can cover areas of

several square millimeters.

There are two ways to intensify the role of the correlated nucleation

process. One of them has been realized by increasing the ratio R, by

amplification of the switching field or by hindering the screening processes.

This possibility has been demonstrated in the above-discussed backswitching

experiments. The alternative possibility is the deposition of the artificial

surface dielectric layer, thus increasing the residual depolarization field. The

period of the quasi-regular structure increases accordingly in this case.

21.7 Modern tricks in nanoscale domain engineering

21.7.1 Backswitch poling

The backswitching process is always considered as undesirable one, because

it destroys the tailored domain structure, but its detailed study is useful. An

original poling method for creation of short-pitch periodical domain structures

in LN and LT, so-called ‘backswitched poling’, has been proposed (Batchko

et al., 1999, 2003; Shur et al., 2000a). The unique feature of backswitched

poling is that the polarization reversal occurs without application of any

external electric field. The domain kinetics is induced by internal source –

residual depolarization field existing after abrupt switch-off of the external

field due to retardation of the bulk screening.

Two distinguishable stages of domain evolution can be revealed during

backswitched poling (Fig. 21.15). The process starts with nucleation of chains

Local field

–2

–3

–4

–5

–6

Depth from 0.1L to 3.9L

0246810

Distance from domain wall

max

–2.0

–2.5

–3.0

1.5

1.0

0.5

0.0

∆

max

(a)

(b)

(c)

0.1 0.2 0.3 0.4 0.5 0.6

Depth

21.14

(a) The simulated local field distributions near the stripe non-

through domain for different depth under the dielectric surface layer.

Depth dependences of (b) value of local field maximum

max

, (c)

distance between the wall and field maximum ∆

max

. The distance

from the domain wall and depth are normalized by the thickness of

the surface dielectric layer

WPNL2204