Афанасьев, Ю.О. Гидрогазомеханика
Подождите немного. Документ загружается.

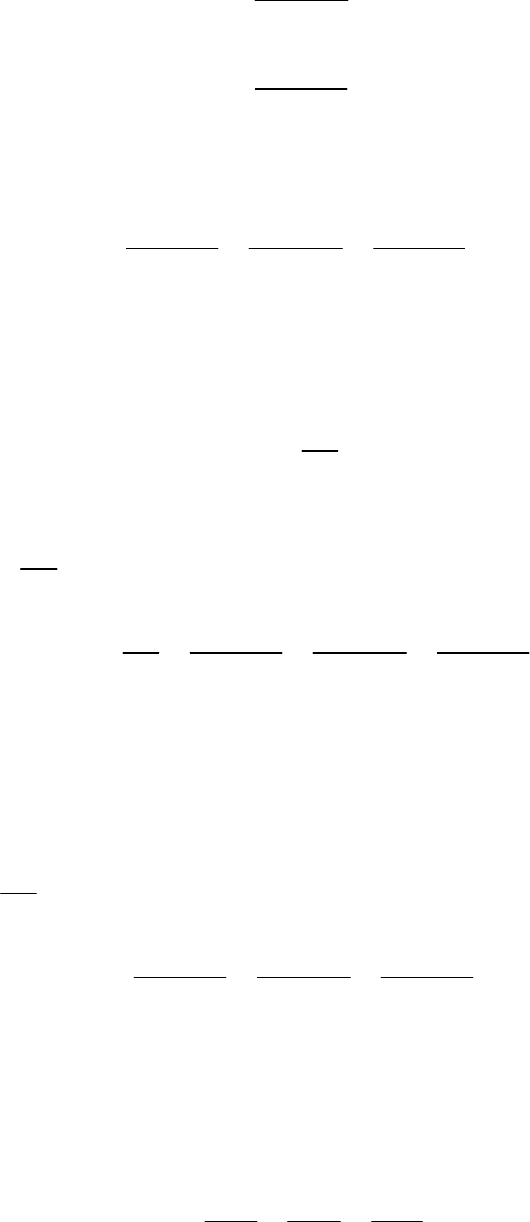
30
тарном объеме вдоль этих осей по аналогии составят:
( )
d d d d d
y
y
w
m y x z t
y
;
( )
d d d d d
z
z
w
m z y x t
z
.
Общее накопление массы жидкости в параллелепипеде за
время dt равно сумме ее приращений вдоль всех осей координат:
( )
( ) ( )
d [ ]d d d d
y
x z
w
w w
m x y z t
x y z
.
Вместе с тем изменение массы в полностью заполненном
жидкостью объеме параллелепипеда возможно только вследствие
изменения плотности жидкости в этом объеме, поэтому
d d d d d
m x y z t
t
.
Приравнивая оба выражения dm, сокращая на (–dxdydzdt)
и перенося
t
в левую часть уравнения, окончательно получим:
( )
( ) ( )
0
y
x z
w
w w
t x y z
. (5.1)
Уравнение (5.1) представляет собой дифференциальное
уравнение неразрывности потока для неустановившегося
движения сжимаемой жидкости.
В установившемся потоке плотность не изменяется во вре-
мени, т.е.
0
t
, и уравнение (5.1) принимает вид
( )
( )
( )
0
y
x z
w
w w
x y z
. (5.2)
Для капельных жидкостей, которые практически несжимае-
мы, а также для газов в условиях изотермического потока при
скоростях, значительно меньших скорости звука, ρ = const и, сле-
довательно,
0
y
x z
w
w w
x y z
. (5.3)
31
Уравнение (5.3) является дифференциальным уравнением
неразрывности потока несжимаемой жидкости.
Сумма изменений скорости вдоль осей координат в левой
части уравнения (5.3) называется дивергенцией вектора скорости
и обозначается через div w. Поэтому данное уравнение можно
представить как
div w = 0. (5.4)
Для того чтобы перейти от элементарного объема ко всему
объему жидкости, движущейся сплошным потоком (без разрывов
и пустот) по трубопроводу переменного сечения, проинтегрируем
дифференциальное уравнение (5.2).
Если бы площадь поперечного сечения трубопровода не из-
менялась, то для стационарного движения вдоль оси х интегри-
рование уравнения (5.2) дало бы зависимость
const
w
,
где w – средняя скорость жидкости.
Если же площадь сечения S трубопровода переменна, то ин-
тегрирование также по площади дает уравнение постоянства
расхода
ρwS = const. (5.5)
Для трех различных сечений трубопровода:
1 1 1 2 2 2 3 3 3
w S w S w S
(5.6)
или
М
1
= М
2
= М
3
,
где М = ρwS – массовый расход жидкости, кг/с.
Выражения (5.5) или (5.6) представляют собой уравнение
неразрывности (сплошности) потока в его интегральной
форме для стационарного движения. Это уравнение называется
также уравнением постоянства расхода.
Согласно уравнению постоянства расхода, при установив-
шемся движении жидкости, полностью заполняющей тру-
бопровод, через каждое его поперечное сечение проходит в
единицу времени одна и та же масса жидкости.
Для капельных жидкостей ρ
1
= ρ
2
= ρ
3
= const и уравнение
(5.6) принимает вид
1 1 2 2 3 3
const
w S w S w S
(5.7)

32
или
Q
1
= Q
2
= Q
3
= const.
Таким образом, уравнение постоянства расхода является
частным случаем закона сохранения массы и выражает мате-
риальный баланс потока.
5.2. Субстациональная производная
По методу Эйлера для каждой частицы движущейся жидко-
сти изменение ее параметров во времени и в пространстве выра-
жается не частной, а полной производной во времени, называе-
мой в гидродинамике субстациональной производной. По сво-
ему смыслу эта производная может быть названа также произ-
водной, следующей за потоком.
Обозначим параметром u любую величину, изменяющуюся
в потоке как во времени, так и пространстве, например: плот-
ность ρ, температуру t, давление р или любую из составляющих
w
x
, w
у
и w
z
ее скорости w в направлениях осей координат.
Допустим, что наблюдатель может мгновенно регистриро-
вать значения u в каждый момент времени в данной точке пото-
ка. Изменение и за единицу времени в фиксированной точке про-
странства (x, y, z) = const выражается частной производной
u t
.
Изменение и в указанной точке за бесконечно малый промежуток
времени dt составляет
d
u
t
t
. Эта величина является местным,
или локальным, изменением данной переменной, которое, как
отмечалось, при стационарном движении равно нулю.
Если наблюдатель перемещается вместе с потоком (с какой-
либо его частицей), то, измеряя значение и, можно установить,
что изменение этой величины складывается из двух составляю-
щих (рис. 13).
Пусть за время dt частица жидкости переместилась из точки
А с координатами (x, y, z)
в точку В с координатами
(x+dx, y+dy, z+dz). В ре-
зультате перемещения
А (x, y, z)
В (x+dx, y+dy, z+dz)
Рис. 13. К выводу выражения
субстационарной производной

33
частицы жидкости в пространстве из точки А
в точку В изменения и, соответствующие проекциям пути dx, dy и
dz, равны
d
u
x
x
,
d
u
y
y
и
d
u
z
z
. Эти изменения не связаны с из-
менением и во времени в какой-либо фиксированной точке про-
странства. Таким образом, если бы движение частицы было уста-
новившимся (
d
u
t
t
= 0), то при переходе из точки А
в точку В изменение и выражалось бы как
d d d d
u u u
u x y z
x y z
.
Это выражение характеризует конвективное изменение
рассматриваемого параметра и.
Вследствие изменения и во времени в каждой точке потока
в условиях нестационарного движения u = f(x, y, z, t), и за время
dt значение указанного параметра также изменится на
d
u
t
t
. Зна-
чит, полное изменение и при нестационарном движении является
суммой локального и конвективного изменений:
d d d d d
u u u u
u t x y z
t x y z
,
откуда производная du по времени
d d d d
d d d d
u u u x u y u z
t t x t y t z t
.
Первая производная координаты по времени является проекцией
вектора скорости на соответствующую ось координат:
d
d
x
x
w
t
,
d
d
y
y
w
t
и
d
d
z
z
w
t
.
Окончательно имеем
d
d
x y z
u u u u u
w w w
t t x y z
. (5.8)
В частном случае стационарного движения жидкости
d
d
x y z
u u u u
w w w
t x y z
. (5.9)
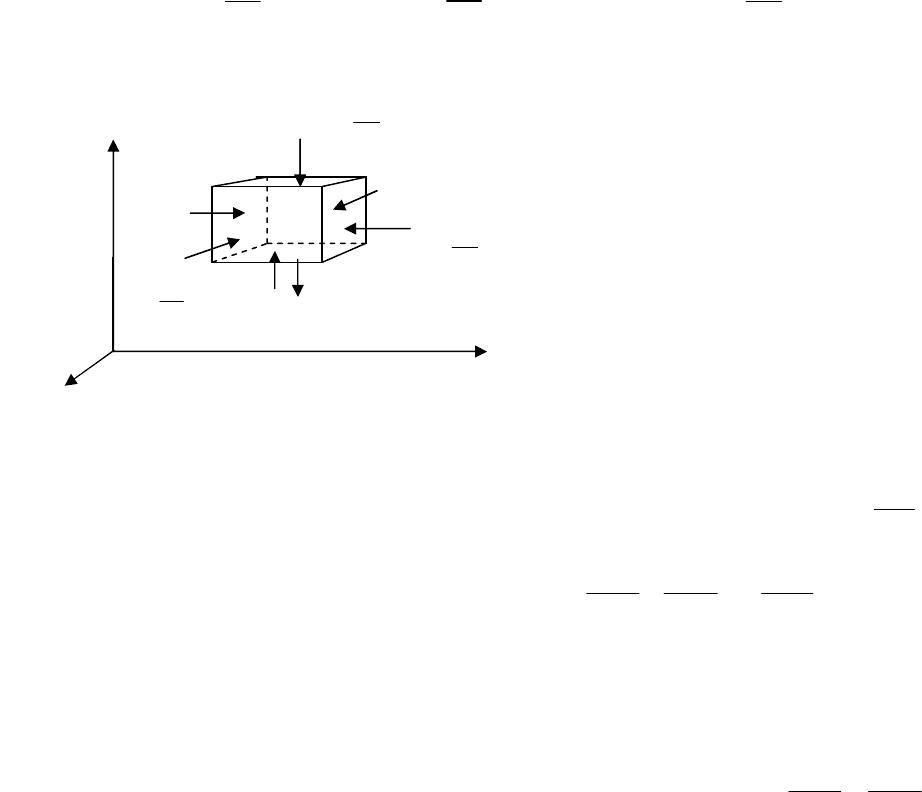
34
Уравнения (5.8), (5.9) выражают субстациональную произ-
водную данного параметра. Субстациональная производная ха-
рактеризует изменение какого-либо параметра или свойства ма-
терии (субстанции) во времени при перемещении материальных
частиц в пространстве.
5.3. Дифференциальные уравнения движения Эйлера
Выделим в стационарном потоке идеальной жидкости эле-
ментарный объем в форме параллелепипеда со сторонами dx, dy,
dz, ориентированными относительно осей координат (рис. 14).
При выводе уравнений равновесия Эйлера было показано,
что проекции на оси координат сил тяжести и давления, дейст-
вующих на параллелепипед, составляют:
для осей: х –
d d d
p
x y z
x
, у –
d d d
p
x y z
y
, z –
d d d .
p
g x y z
z
Согласно принципу динамики, сумма проекций сил, дей-
ствующих на движущий-
ся элементарный объем
жидкости, равна произ-
ведению массы жидкости
на ее ускорение.
Масса жидкости
в объеме параллелепипеда
d d d d
m x y z
.
Если жидкость дви-
жется со скоростью w, то
ее ускорение равно
d
d
w
t
,
а проекции ускорения на оси координат
d
d
x
w
t
,
d
d
y
w
t
и
d
d
z
w
t
, где w
x
,
w
y
и w
z
– составляющие скорости вдоль осей x, y и z. Разумеется,
при этом соответствующие производные по времени не означают
изменений во времени составляющих скорости в какой-либо
фиксированной точке пространства. Такие изменения
x
w
t
,
y
w
t
Рис. 14. К выводу дифференциальных
уравнений движения Эйлера
y
z
d
p
p z
z
d
p
p x
x
d
p
p y
y
x
gdm
p
p
p
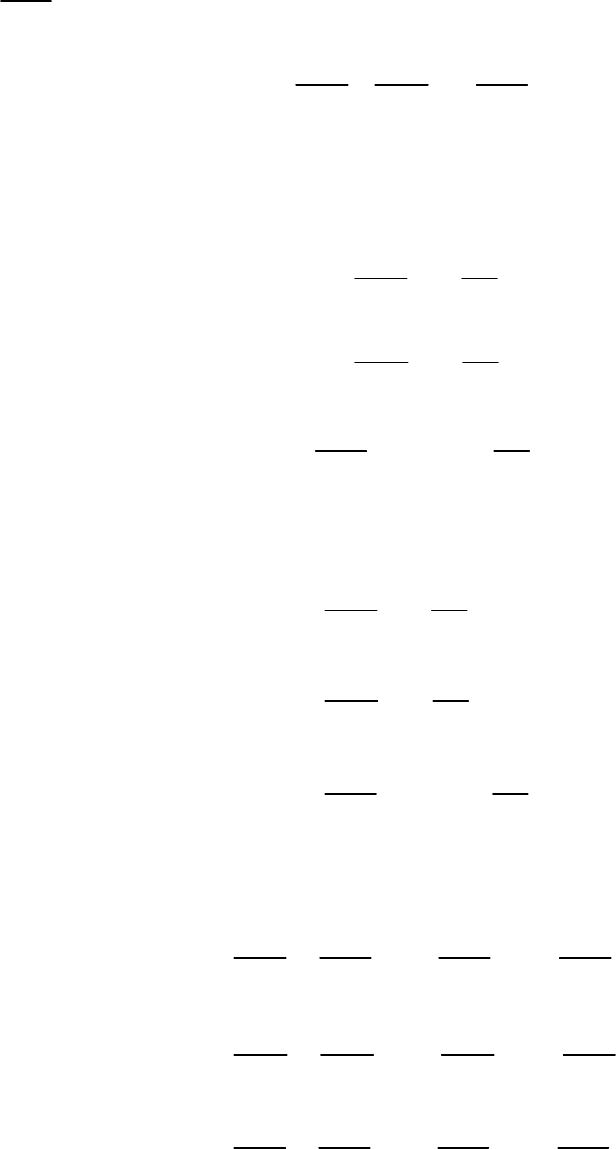
35
и
z
w
t
равны нулю в рассматриваемом случае стационарного по-
тока. Производные же
d
d
x
w
t
,
d
d
y
w
t
и
d
d
z
w
t
отвечают изменению во
времени значений w
x
, w
y
и w
z
при перемещении частицы жидко-
сти из одной точки пространства (потока) в другую.
В соответствии с принципом динамики
d
d d d d d d
d
x
w
p
x y z x y z
t x
;
d
d d d d d d
d
y
w
p
x y z x y z
t y
;
d
d d d ( )d d d
d
z
w p
x y z g x y z
t z
.
Или после сокращения
d
;
d
d
;
d
d
,
d
x
y
z
w p
t x
w
p
t y
w
p
g
t z
(5.10)
где, согласно уравнению (5.9), субстациональные производные
соответствующих составляющих скорости равны
d
;
d
d
;
d
d
.
d
x x x x
x y z
y y y y
x y z
z z z z
x y z
w w w w
w w w
t x y z
w w w w
w w w
t x y z
w w w w
w w w
t x y z
(5.11)
Система уравнений (5.10) с учетом выражений (5.11) пред-
ставляет собой дифференциальные уравнения движения иде-
альной жидкости Эйлера для установившегося потока.

36
При неустановившемся движении скорость жидкости изме-
няется не только при перемещении частицы потока из одной точ-
ки пространства в другую, но и с течением в каждой точке. По-
этому, в соответствии с уравнением (5.8), составляющие ускоре-
ния в уравнении (5.10), выражаемые субстациональными произ-
водными для нестационарного потока, имеют следующий вид:
d
;
d
d
;
d
d
.
d
x x x x x
x y z
y y y y y
x y z
z z z z z
x y z
w w w w w
w w w
t t x y z
w w w w w
w w w
t t x y z
w w w w w
w w w
t t x y z
(5.12)
Система уравнений (5.10) с учетом выражений (5.12) пред-
ставляет собой дифференциальные уравнения движения иде-
альной жидкости Эйлера для неустановившегося потока.
Интегралом уравнений движения Эйлера для стационарного
потока является уравнение Бернулли, широко используемое для
решения многих технических задач.
5.4. Уравнение Бернулли
Умножим левые и правые части каждого из уравнений
(5.10) соответственно на dx, dy и dz и, разделив на плотность ρ
жидкости, получим
d 1
d d
d
x
x p
w x
t x
;
d 1
d d
d
y
y p
w y
t y
;
d 1
d d d
d
z
z p
w g z z
t z
.
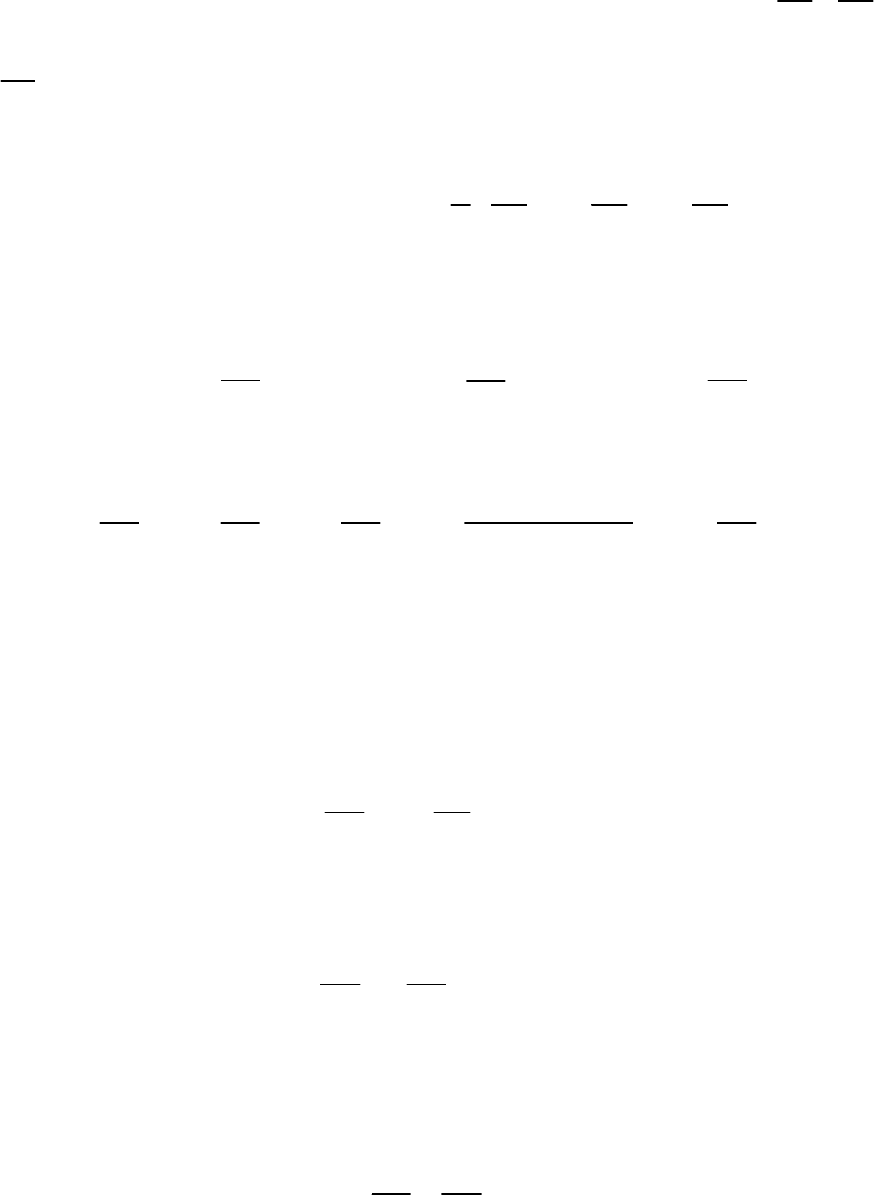
37
Сложим эти уравнения, учитывая, что производные
d
d
x
t
,
d
d
y
t
и
d
d
z
t
выражают проекции w
x
, w
y
и w
z
скорости на соответствую-
щие оси координат. Тогда
1
d d d d d d d
x x y y z z
p p p
w w w w w w g z x y z
x y z
. (5.13)
Слагаемые левой части этого уравнения могут быть пред-
ставлены как
2
d d
2
x
x x
w
w w
,
2
d d
2
y
y y
w
w w
,
2
d d
2
z
z z
w
w w
.
Следовательно, их сумма
2 2 2 2
2
2
2
d d d d d
2 2 2 2 2
y x y z
x
z
w w w w
w
w
w
,
где w – скорость, составляющие которой вдоль соответствующих
осей равны w
x
, w
y
и w
z
.
Сумма членов, стоящих в скобках в правой части уравнения
(5.13), представляет собой полный дифференциал давления dp,
следовательно, это уравнение можно представить:
2
d
d d
2
w p
g z
.
Разделив обе части этого уравнения на ускорение свободно-
го падения g и перенеся все его члены в левую часть, находим:
2
d
d d 0
2
w p
z
g g
,
причем для несжимаемой, однородной жидкости ρ = const.
Сумма дифференциалов может быть заменена дифферен-
циалом суммы; следовательно,
2
d 0
2
p w
z
g g
,
откуда после интегрирования

38
2
const
2
p w
z
g g
. (5.14)
Уравнение (5.14) для любых двух поперечных сечений 1 и 2
потока можно представить в виде
2 2
1 1 2 2
1 2
2 2
p w p w
z z
g g g g
. (5.15)
Уравнение (5.14) является уравнением Бернулли для иде-
альной жидкости.
Величину
2
2
p w
z
g g
называют полным гидродинами-
ческим напором, или просто гидродинамическим напором.
Следовательно, согласно уравнению Бернулли, для всех по-
перечных сечений стационарного потока идеальной жидко-
сти гидродинамический напор остается постоянным.
Гидродинамический напор включает три слагаемых, из ко-
торых первые два слагаемых, z и
p
g
, входили в основное урав-
нение гидростатики (2.13): z – нивелирная высота, называемая
также геометрическим, или высотным, напором (h
г
), представ-
ляет собой удельную потенциальную энергию положения
в данной точке (данном сечении);
p
g
– напор давления (h
давл
),
или пьезометрический напор (высота), характеризует удель-
ную потенциальную энергию давления в данной точке (данном
сечении);
2
2
w
g
– представляет собой скоростной, или динамиче-
ский, напор (h
ск
), он характеризует удельную кинетическую
энергию
в данной точке (данном сечении).
Все три составляющих уравнения Бернулли могут быть вы-
ражены как в единицах длины, так и в единицах удельной энер-
гии, т.е. энергии, приходящейся на единицу веса жидкости, на-
пример, скоростной напор:

39
2 2 2
2
м с
м
2 с м
w
g
;
2
Ô Õ Ö×
2 Ô Ô
w
g
.
Таким образом, согласно уравнению Бернулли, при уста-
новившемся движении идеальной жидкости сумма
скоростного и статического напоров, равная гидродина-
мическому напору, не меняется при переходе от одного
поперечного сечения потока к другому.
Вместе с тем из уравнения Бернулли в соответствии с энер-
гетическим смыслом его членов следует, что при стационарном
движении идеальной жидкости сумма потенциальной
p
z
g
и кинетической
2
2
w
g
энергии жидкости для каждо-
го из поперечных сечений потока остается неизменной.
При изменении поперечного сечения трубопровода и соот-
ветственно скорости движения жидкости происходит превраще-
ние энергии. При сужении трубопровода часть потенциальной
энергии давления переходит в кинетическую и, наоборот, при
расширении трубопровода часть кинетической энергии перехо-
дит в потенциальную. Однако общее количество энергии для по-
тока идеальной жидкости остается постоянным.
Таким образом, уравнение Бернулли является частным
случаем закона сохранения энергии и выражает энергетиче-
ский баланс потока.
Рассмотрим применение уравнения Бернулли на примере
потока идеальной жидкости, движущейся через произвольно рас-
положенный в пространстве трубопровод переменного сечения
(рис. 15). Пусть для точек, лежащих на оси трубопровода в попе-
речных сечениях 1-1 и 2-2, нивелирные высоты равны z
1
и z
2
со-
ответственно. Установим в каждой из этих точек две вертикаль-
ные открытые так называемые пьезометрические трубки (на-
порные трубки Пито – Прандтля), у одной из которых нижний
конец загнут навстречу потоку жидкости в трубопроводе (так на-
зываемая трубка Пито). Прямую трубку называют трубкой
Прандтля.
