Афанасьев, Ю.О. Гидрогазомеханика
Подождите немного. Документ загружается.


50
2
2
Re
w l wl
w l
. (7.3)
Полученный безразмерный комплекс величин
wl
называ-
ется, как известно, критерием Рейнольдса.
Таким образом, критерий Рейнольдса отражает влияние
силы трения на движение жидкости. Он характеризует отно-
шение инерционных сил к силам трения в подобных потоках.
Величина l в критерии Re, как и в других критериях подо-
бия, представляет собой определяющий линейный размер. При
движении жидкости через трубопроводы или аппараты за такой
размер принимается их диаметр d, а в случае некруглого сечения
потока – эквивалентный диаметр d
э
.
При неустановившемся движении жидкости в уравнении
Навье – Стокса
0
z
w
t
. Заменив член, отражающий влияние не-
стационарности движения (
z
w
w
t t
), охарактеризуем соотно-
шение между силой инерции и этой величиной:
2
w l wt
w t l
.
Безразмерный комплекс
wt
l
называется критерием гомо-
хронности и обозначается через Но. Следовательно,
Ho
wt
l
. (7.4)
Критерий гомохронности учитывает нестационарный
характер движения в подобных потоках.
7.2. Критериальное уравнение гидродинамики
Во всех сходственных точках движущихся подобно жидко-
стей
Fr = Fr , Eu = Eu , Re = Re , Ho = Ho
.
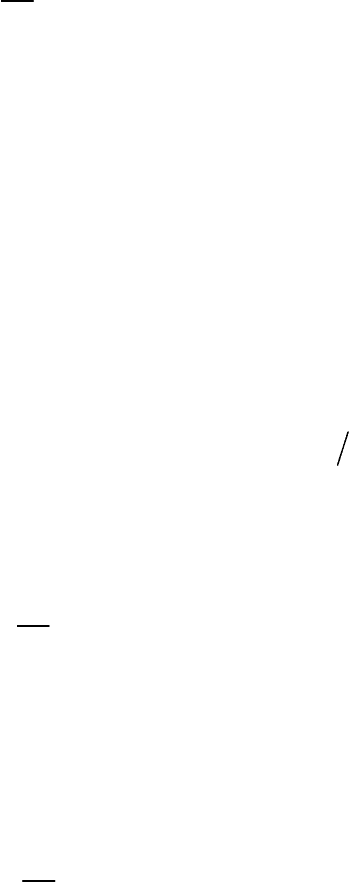
51
Согласно второй теореме подобия, решение уравнений На-
вье – Стокса можно представить в виде функциональной зависи-
мости между полученными критериями подобия, т.е.
(Ho, Fr, Eu, Re) 0
. (7.5)
В ряде случаев зависимость (7.5) должна быть дополнена
симплексами геометрического подобия. При движении жидкости
через трубы или каналы таким симплексом является отношение
длины l трубы к ее диаметру d или эквивалентному диаметру d
э
.
Тогда критериальное уравнение принимает вид
э
(Ho, Fr, Eu, Re, ) 0
l
d
. (7.6)
При наиболее важной для практики формулировке задачи
(определение потери давления Δр) все входящие в уравнение
критерии, кроме критерия Эйлера, служат определяющими, так
как они составлены исключительно из величин, выражающих ус-
ловие однозначности. В критерий же Эйлера входит величина
Δр, значение которой при движении жидкости в трубе полностью
обусловливается формой трубы (отношением l/d
э
), физическими
свойствами жидкости (μ, ρ) и распределением скоростей у входа
в трубу и у ее стенок (начальные и граничные условия). Поэтому,
согласно третьей теореме подобия, для подобия необходимо
и достаточно соблюдение равенства значений
э
Ho, Fr, Re,
l d
.
Следствием выполнения этих условий будет также равенство
значений определяемого критерия Eu в сходственных точках по-
добных потоков. Поэтому уравнение (7.6) представляют как
э
Eu = (Ho, Fr, Re, )
l
f
d
. (7.7)
Зависимости (7.5), (7.6) или (7.7) называют обобщенным
или критериальным уравнением гидродинамики.
Функцию (7.7) наиболее часто аппроксимируют степенной
зависимостью, т.е. придают этой функции вид
Eu = Ho Fr Re
q
m n p
˜
l
A
d
. (7.8)

52
Путем обработки опытных данных, полученных на моделях,
находят числовые значения коэффициента А и показателей сте-
пеней m, n, p, q при соответствующих критериях.
Глава 8. Уравнение Бернулли для реальной
(вязкой) жидкости
При движении реальных жидкостей начинают действовать
силы внутреннего трения, обусловленные вязкостью жидкости
и режимом ее движения, а также силы трения о стенки трубы.
Эти силы оказывают сопротивление движению жидкости. На
преодоление возникающего гидравлического сопротивления
должна расходоваться некоторая часть энергии потока. Поэтому
общее количество энергии потока по длине трубопровода будет
непрерывно уменьшаться вследствие перехода потенциальной
энергии в потерянную энергию – затраченную на трение и без-
возвратно теряемую при рассеивании тепла в окружающую сре-
ду.
Для двух любых сечений 1-1 и 2-2 трубопровода, располо-
женных по ходу движения потока реальной жидкости
(см. рис. 15), запишем уравнение Бернулли:
2 2
1 1 2 2
1 2
2 2
p w p w
z z
g g g g
.
Для соблюдения баланса энергии при движении реальной
жидкости в правую часть уравнения (5.15) должен быть введен
член, выражающий потерянный напор. Тогда получим уравнение
Бернулли для реальных жидкостей:
2 2
1 1 2 2
1 2
п
2 2
p w p w
z z h
g g g g
. (8.1)
Потерянный напор h
п
характеризует удельную (т.е. отнесен-
ную к единице веса жидкости) энергию, расходуемую на пре-
одоление гидравлического сопротивления при движении
реальной жидкости.
Уравнение (8.1) можно представить в другом виде, если ум-
ножить обе его части на ρg:

53
2 2
1 2
1 1 2 2
2 2
w w
gz p gz p p
. (8.2)
В уравнении (8.2) величина Δр – потерянное давление,
равное
Ø
p gh
. (8.3)
Определение потерь напора или гидравлических потерь яв-
ляется для практики важной задачей, связанной с расчетом энер-
гии, которая необходима для перемещения реальных жидкостей
при помощи насосов, компрессоров и т.д.
8.1. Гидравлические потери
Расчет гидравлического сопротивления при движении ре-
альных жидкостей по трубопроводам является одним из основ-
ных прикладных вопросов гидродинамики.
Потери напора в трубопроводе в общем случае обуслов-
ливаются сопротивлением трения и местными сопротивле-
ниями.
Сопротивление трения, называемое также сопротивлени-
ем по длине, существует при движении реальной жидкости по
всей длине трубопровода. На него оказывает влияние режим те-
чения жидкости (ламинарный, турбулентный, степень развития
турбулентности). Так, турбулентный поток характеризуется не
только ¬ньютоновской°, но и турбулентной вязкостью, которая
зависит от гидродинамических условий и вызывает дополни-
тельные потери энергии при движении жидкости.
Местные сопротивления возникают при любых измене-
ниях значения скорости потока или ее направления. К их
числу относятся вход потока в трубу и выход из нее жидкости,
внезапные сужения и расширения труб, отводы, колена, тройни-
ки, запорные и регулирующие устройства (краны, вентили, за-
движки)
и др.
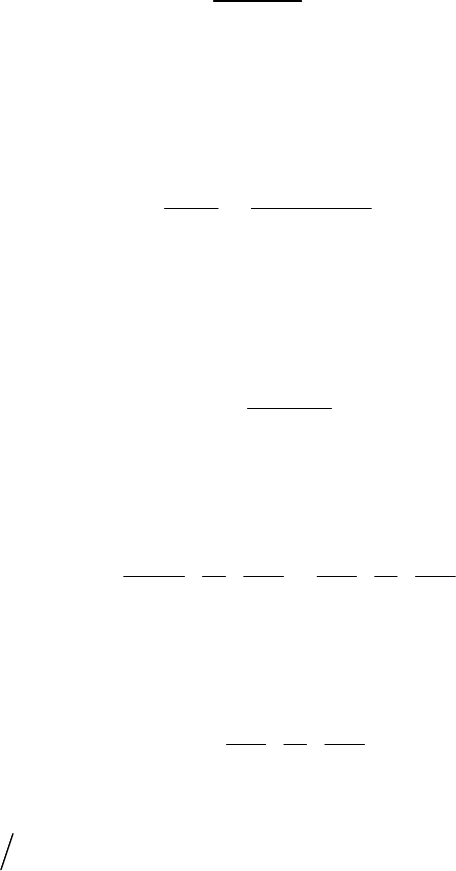
h
п
= h
тр
+ h
мс
,
где h
тр
и h
мс
– потери напора вследствие трения и местных сопро-
тивлений соответственно.
54
8.2. Расчет потерь на трение
В случае ламинарного движения по прямой трубе потеря
напора на трение (т.е. его потеря по длине) h
тр
может быть опре-
делена теоретически на основании уравнения Пуазейля (9.7):
4
128
d p
Q
l
. (8.4)
При подстановке уравнения (8.3) в уравнение (8.4) и замене
объемного расхода Q произведением средней скорости потока w
на площадь поперечного сечения трубы πd
2
/4 получим
4
2
тр
4 128
d gh
d
w
l
,
где l и d – длина и диаметр трубы; μ и ρ – вязкость и плотность
жидкости.
После сокращений потерянный напор равен
тр
2
32
w l
h
gd
.
Умножая числитель и знаменатель правой части на 2w
и группируя величины, окончательно получим:
2 2
тр
64 64
2 Re 2
l w l w
h
wd d g d g
.
Таким образом, при ламинарном движении по прямой круг-
лой трубе
2
тр
64
Re 2
l w
h
d g
, (8.5)
т.е. потерянный на трение напор выражается через скоростной
напор
2
ск
2
h w g
.
Величину, показывающую, во сколько раз напор, потерян-
ный на трение, отличается от скоростного напора, называют ко-
эффициентом потерь энергии по длине, или коэффициентом
сопротивления трения, и обозначают символом ζ
тр
, а отноше-
ние 64/Re, входящее в эту величину, – коэффициентом гидравли-
ческого трения, или коэффициентом трения, и обозначают через
λ. Поэтому

55
64
Re
и
тр
l
d
.
Следовательно, уравнение (8.5) может быть представлено
в виде
2 2
тр тр
2 2
w l w
h
g d g
(8.6)
или для потери давления (с учетом того, что
тр тр
p gh
)
2
тр
2
l w
p
d
. (8.7)
Уравнение (8.7) при λ = 64/Re хорошо согласуется с опыт-
ными данными для установившегося ламинарного движения
(Re < 2320). В этих условиях коэффициент трения практически
не зависит от шероховатости стенок трубопровода.
Для каналов некруглого сечения в уравнение (8.7) вместо
диаметра d подставляют эквивалентный диаметр d
э
, причем
Re
B
, (8.8)
где В – коэффициент, значение которого зависит от формы попе-
речного сечения (для квадратного сечения В = 57, для кольцевого
сечения В = 96 и т.д.).
Уравнение того же вида, что и уравнение (8.6), может быть
использовано для определения потерь напора на трение также
при турбулентном движении жидкости. Однако выражение для
коэффициента трения в данном случае не может быть выведено
теоретически из-за сложности структуры турбулентного потока
и невозможности решения для него уравнений Навье – Стокса.
Поэтому расчетные уравнения для определения λ при турбулент-
ном движении получают обобщением результатов экспериментов
методом теории подобия.
В диапазоне чисел Re до 10
5
коэффициент трения в гладких
трубах с круглым поперечным сечением определяется по эмпи-
рической формуле, называемой законом сопротивления Бла-
зиуса:
4
0,316
Re
. (8.9)

56
Для чисел Re вплоть до 3,4∙10
6
экспериментальные данные
Никурадзе [8] хорошо описываются эмпирическим уравнением,
которое называют универсальным законом сопротивления
Прандтля для гладких труб:
1
2lg Re 0,8
. (8.10)
При турбулентном потоке коэффициент трения в общем
случае зависит не только от характера движения жидкости (зна-
чения Re), но и от шероховатости стенок труб. Шероховатость
труб может быть количественно оценена некоторой усредненной
величиной абсолютной шероховатости е, представляющей со-
бой среднюю высоту выступов шероховатости на внутренней по-
верхности труб.
Влияние шероховатости на величину λ определяется соот-
ношением между средней высотой выступов шероховатости е
и толщиной вязкого подслоя δ, движение жидкости в котором
можно считать практически ламинарным. В некоторой началь-
ной области турбулентного движения, когда толщина вязкого
подслоя больше высоты выступов шероховатости (δ > е), жид-
кость плавно обтекает эти выступы и влиянием шероховатости
на величину λ можно пренебречь. В указанной области турбу-
лентного движения трубы можно рассматривать как гидравличе-
ски гладкие и вычислять по уравнениям (8.9) и (8.10).
При возрастании Re величина δ уменьшается. Когда она
становится сравнимой с абсолютной шероховатостью (δ ≈ е) и
меньше ее (δ < е), вязкий подслой уже не покрывает выступов
шероховатости. В таких условиях коэффициент трения все боль-
ше начинает зависеть от шероховатости. При этом величина λ,
а следовательно, и потеря напора на трение возрастают под дей-
ствием сил инерции, возникающих вследствие дополнительного
вихреобразования вокруг выступов шероховатости.
Таким образом, с увеличением критерия Рейнольдса зона
гладкого трения, в которой λ зависит лишь от Re, переходит
сначала в зону смешанного трения, когда на величину λ влияют
и Re и шероховатость. Затем течение переходит в автомодель-
ную (по отношению к Re) зону, когда величина λ практически
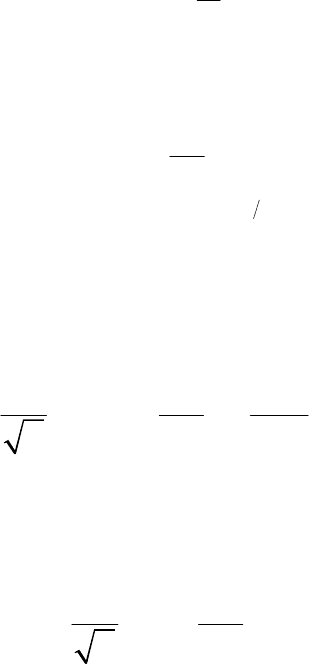
57
перестает зависеть от критерия Рейнольдса и определяется лишь
шероховатостью стенок труб.
Автомодельную область называют также областью квадра-
тичного закона сопротивления, так как согласно уравнению
(8.6) при отсутствии влияния Re (т.е. скорости) на величину λ со-
противление трения становится пропорциональным квадрату
скорости.
Критические значения Re
кр1
, при которых начинается зона
смешанного трения, а также критические значения Re
кр2
, при ко-
торых λ становится функцией только шероховатости трубы (ав-
томодельная зона), зависят от относительной шероховатости ε,
выражаемой отношением абсолютной шероховатости е к диамет-
ру d трубы:
e
d
.
Значения Re
кр1
и Re
кр2
ориентировочно определяют по урав-
нениям
кр1
23
Re
e
; (8.11)
9 8
кр2
Re 220
ε
. (8.12)
При расчете коэффициента трения для всех областей (зон)
турбулентного движения применимо общее уравнение (формула
Альтшуля):
0,9
1 6,81
2lg
3,7 Re
. (8.13)
Для автомодельной области, когда λ перестает зависеть от
Re, в уравнении (8.13) можно пренебречь вторым слагаемым
в квадратных скобках, и оно принимает вид
1 3,7
2lg
. (8.14)
8.3. Расчет потерь на местных сопротивлениях
В различных местных сопротивлениях происходят измене-
ния значения скорости потока по величине (рис. 17, а, б) и на-

58
правлению (рис. 18, а, б) или одновременно (рис. 19, а, б, в). При
этом возникают дополнительные, необратимые потери энергии
(напора), кроме потерь, связанных с трением [7].
При внезапном увеличении сечения трубы (см. рис. 17, а)
напор теряется вследствие удара потока, выходящего с большой
скоростью из части трубопровода с меньшим диаметром, о по-
ток, движущийся медленнее в части трубопровода с большим
диаметром. При этом в области, примыкающей к прямому углу
трубы более широкого сечения, возникают обратные токи-
завихрения, на образование которых бесполезно тратится часть
энергии. При внезапном сужении трубопровода (см. рис. 17, б)
дополнительная потеря энергии обусловлена тем, что сечение по-
тока сначала становится меньше сечения самой трубы и лишь за-
тем поток расширяется, заполняя всю трубу.
При изменении направления потока (см. рис. 18, а, б) обра-
зование завихрений происходит вследствие действия инерцион-
ных (центробежных) сил.
При движении жидкостей через запорно-регулирующие уст-
ройства дополнительные потери энергии обусловлены изменени-
ем направления потока и его скорости (см. рис. 19, а, б, в).
Рис. 17. Местные сопротивле
ния
с изменением скорости потока:
а – внезапное расширение;
б – внезапное сужение
Рис. 18. Местные сопротивления
с изменением направления потока:
а – резкий поворот на 90Ù (колено);
б
–
плавный поворот на 90
Ù
(о
т
вод)
б
а
б
а
Рис. 19. Запорно-регулирующие устройства
как местные сопротивления:
а – пробковый кран; б – стандартный вентиль; в – прямоточный вен-
тиль
а б в

59
Потери напора в местных сопротивлениях, как и потери на
трение, выражают через скоростной напор. Отношение потери
напора в данном местном сопротивлении h
мс
к скоростному на-
пору h
ск
называют коэффициентом местного сопротивления
и обозначают через ζ
мс
. Следовательно, для различных местных
сопротивлений
2
мс1 мс1
2
w
h
g
;
2
мс2 мс2
2
w
h
g
;
2
Õ Ú Õ c
2
n n
w
h
g
,
или суммарно – для всех местных сопротивлений трубопровода
2
мс
мс
2
w
h
g
. (8.15)
Коэффициенты различных местных сопротивлений в боль-
шинстве случаев находят опытным путем. Их средние значения
приводятся в справочной литературе [7].
Таким образом, потеря напора находится по уравнению
2
п мс
э
2
l w
h
d g
. (8.16)
Соответственно, потеря давления (с учетом того, что Δр
п
= ρgh
п
)
2
Ø Õ Ú
Û
2
l w
p
d
. (8.17)
Величина h
п
в уравнении (8.16) выражается в метрах столба
жидкости и не зависит от рода жидкости, а потери давления Δр
п
зависят от ее плотности.
Глава 9. Ламинарный режим движения жидкости
Отыскание точных решений уравнений Навье – Стокса на-
талкивается в общем случае на непреодолимые математические
трудности. Тем не менее, в некоторых частных случаях все же
