Alligood K., Sauer T., Yorke J.A. Chaos: An Introduction to Dynamical Systems

Подождите немного. Документ загружается.

7.3 LINEAR D IFFERENTIAL E QUATIONS IN M ORE THAN O NE D IMENSION

v(t) ⫽ c

␭

⫹ c

␭

, for real constants c

and c

. The constants need to be

chosen to ﬁt the initial values.

For example, suppose we want the solution with initial condition v(0) ⫽

(1, 1) at t ⫽ 0. Setting t equal to 0 in the general solution gives v(0) ⫽ c

⫹

. Written in coordinates, we have c

(1, ⫺2) ⫹ c

(3, ⫺1) ⫽ (1, 1). Solving

gives c

⫽⫺4 5andc

⫽ 3 5. Thus the speciﬁc solution to this initial value

problem is v(t) ⫽⫺4 5e

⫹ 3 5e

⫺3t

. This solution corresponds to the up-

permost curve in Figure 7.7. As t becomes large, the u

term becomes negligible, so

that this curve asymptotically approaches the line L

deﬁned by the direction u

The eigenvectors corresponding to a particular eigenvalue

␭

together with

the origin form a linear subspace, called the eigenspace corresponding to

␭

. In

Figure 7.7 the straight lines are the eigenspaces; the steeper line L

is all multiples

of (1, ⫺2), and the other line L

consists of all multiples of (3, ⫺1). The two

eigenspaces play important roles in the long-time dynamics of (7.16). All initial

values v(0) lying on L

approach the origin as t increases. All initial values except

those on L

approach L

in the limit as t →

⬁

In this example, the eigenvectors together span the entire phase space ⺢

In other cases, it is possible that the sum of the dimensions of all the eigenspaces

does not equal the dimension of the phase space. In the following example, there

is a single eigenvalue and a single linearly independent eigenvector, even though

the phase space is two dimensional.

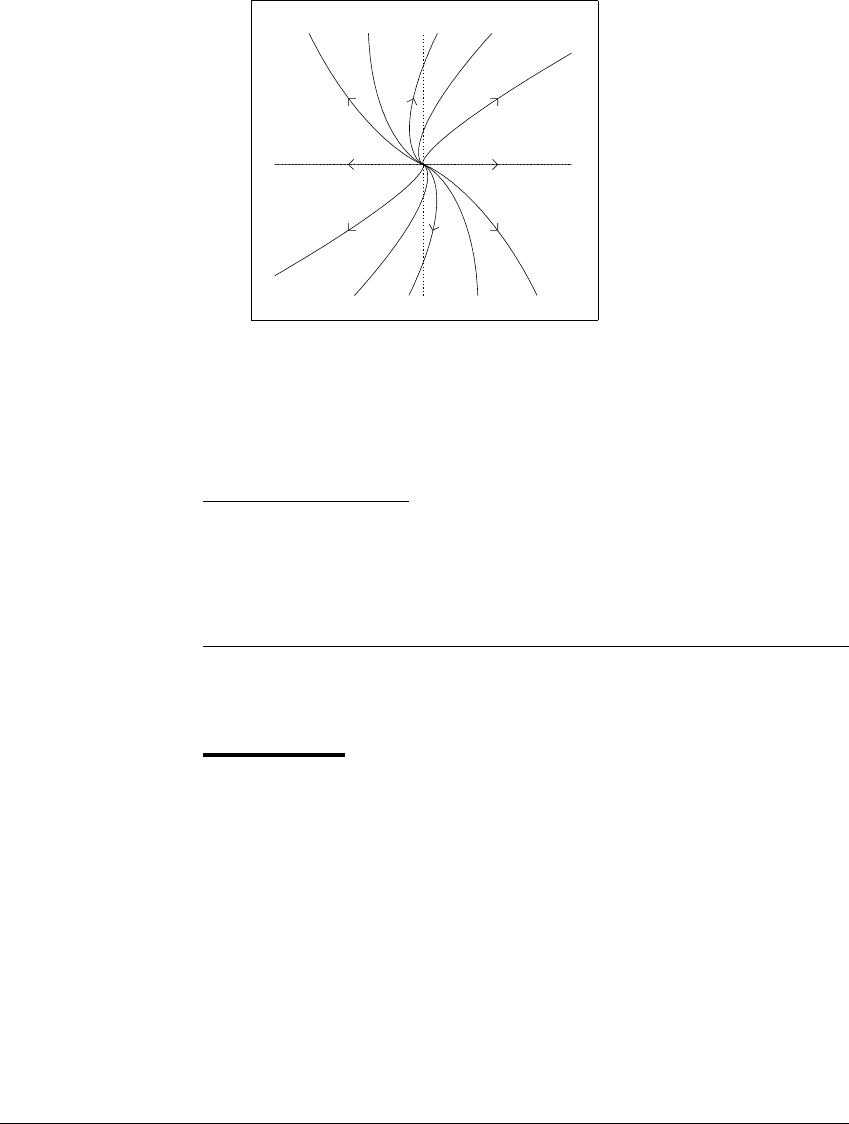
E XAMPLE 7.6

Let

x ⫽ 3x ⫹ y

y ⫽ 3y (7.17)

The coefﬁcient matrix

A ⫽





has only one eigenvalue

␭

⫽ 3, and (1, 0) is the only eigenvector up to scalar

multiple. The phase plane for this system is shown in Figure 7.8. The x-axis is the

eigenspace; it contains all positive and negative scalar multiples of (1, 0).

For simplicity we sometimes refer to the eigenvectors and eigenvalues of a

linear differential equation like (7.17) when we actually mean the corresponding

matrix A. We would say for example that

␭

⫽ 3 is an eigenvalue of (7.17).

287

D IFFERENTIAL E QUATIONS

Figure 7.8 Phase plane for Equation (7.17).

The coefﬁcient matrix A for this system has only one eigenvector, which lies along

the x-axis. All solutions except for the equilibrium diverge to inﬁnity.

✎ E XERCISE T7.2

(a) Verify the statements made in Example 7.6. (b) Find all solution curves

of (7.17). Solve for y(t) ﬁrst, then try to guess the form of a solution for

x(t).

When the eigenvalues are complex, there are no corresponding real eigen-

vectors. We give two examples:

E XAMPLE 7.7

Let

x ⫽ y

y ⫽⫺x. (7.18)

Verify that the eigenvalues are ⫾i. Solutions of this system are x(t) ⫽ c

cos t ⫹

sin t and y(t) ⫽ c

cos t ⫺ c

sin t, where c

and c

are any real constants. The

phase plane is shown in Figure 7.9. We will show that each solution remains

a constant distance from the origin. If v(t) ⫽ (x(t),y(t)) is a solution, then

the distance squared is |v(t)|

⫽ x

⫹ y

. Differentiating this expression gives

x ⫹ 2y

y, which, from (7.18) is 2xy ⫺ 2yx ⫽ 0. Thustherateofchangeofthe

288

7.3 LINEAR D IFFERENTIAL E QUATIONS IN M ORE THAN O NE D IMENSION

(a) (b)

Figure 7.9 Phase planes for pure imaginary eigenvalues.

(a) In (7.18), the eigenvalues are ⫾i. All solutions are circles around the origin,

which is an equilibrium. (b) In (7.23), the eigenvalues are again pure imaginary.

Solutions are elliptical. Note that for this equilibrium, some points initially move

farther away, but not too far away. The origin is (Lyapunov) stable but not attracting.

distance from the origin is 0, meaning that |v(t)|

and |v(t)| are constant. For

those familiar with inner products, another way to see that solutions lie on circles

about the origin is to note that at any point (x, y), the velocity vector (y, ⫺x)is

perpendicular to the position vector (x, y). Hence the instantaneous motion is

neither toward nor away from (0, 0). Since this property holds at all points, |v(t)|

never changes.

✎ E XERCISE T7.3

Explain why the trajectories in the phase planes of Figure 7.9(a) circle the

origin clockwise.

E XAMPLE 7.8

A more general version of the above example is

x ⫽ ax ⫺ by

y ⫽ bx ⫹ ay. (7.19)

289

D IFFERENTIAL E QUATIONS

Verify that the eigenvalues are a ⫾ bi. Solutions of this system are

x(t) ⫽ e

cos bt ⫹ c

sin bt)

y(t) ⫽ e

(⫺c

cos bt ⫹ c

sin bt), (7.20)

where c

and c

are any real constants. Check this solution by differentiating.

E XAMPLE 7.9

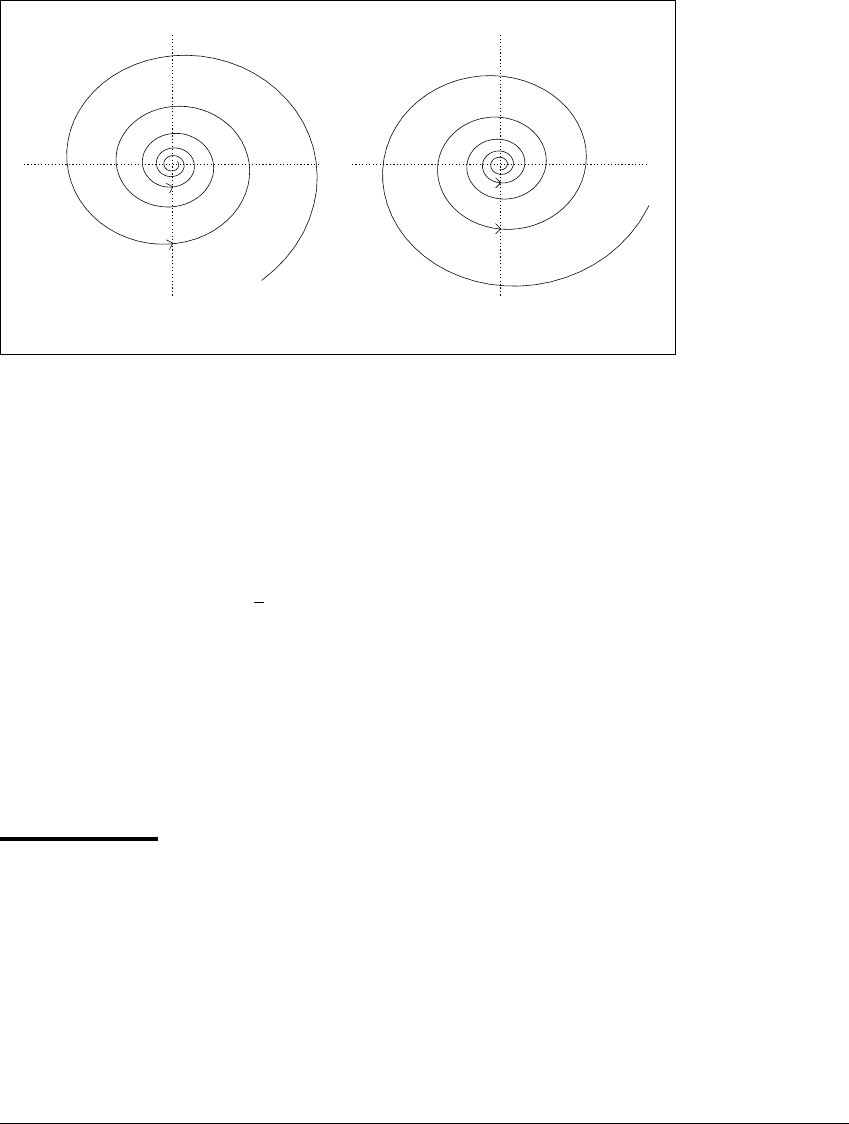
Here are two particular cases of Example 7.8. Let

x ⫽⫺x ⫺ 10y

y ⫽ 10x ⫺ y. (7.21)

Verify that the eigenvalues are ⫺1 ⫾ 10i. Solutions of this system are x(t) ⫽

⫺t

cos 10t ⫹ c

sin 10t)andy(t) ⫽ e

⫺t

(⫺c

cos 10t ⫹ c

sin 10t), where c

and

are any real constants. The constants c

and c

are determined by matching

initial conditions. All solutions spiral in toward the origin.

The slightly different system

x ⫽ x ⫺ 10y

y ⫽ 10x ⫹ y (7.22)

has eigenvalues 1 ⫾ 10i, and the solutions have form x(t) ⫽ e

cos 10t ⫹

sin 10t)andy(t) ⫽ e

(⫺c

cos 10t ⫹ c

sin 10t). Solutions of this system spi-

ral out from the origin.

See Figure 7.10 for a sketch of the phase planes of these two systems. The

difference between them is that the origin is attracting when the eigenvalues of

the right-hand side matrix have negative real part, and repelling when they have

positive real part.

Deﬁnition 7.10 An equilibrium point

v is called stable or Lyapunov

stable if every initial point v

that is chosen very close to v has the property that

the solution F(t, v

) stays close to v for t ⱖ 0. More formally, for any neighborhood

N of

v there exists a neighborhood N

of v, contained in N, such that for

each initial point v

in N

, the solution F(t, v

)isinN for all t ⱖ 0. An

equilibrium is called asymptotically stable if it is both stable and attracting. An

equilibrium is called unstable if it is not stable. Finally, an equilibrium is globally

asymptotically stable if it is asymptotically stable and all initial values converge

to the equilibrium.

290

7.3 LINEAR D IFFERENTIAL E QUATIONS IN M ORE THAN O NE D IMENSION

(a) (b)

Figure 7.10 Phase planes for complex eigenvalues with nonzero real part.

(a) Under (7.21), trajectories spiral in to a sink at the origin. The eigenvalues of the

coefﬁcient matrix A have negative real part. (b) For (7.22), the trajectories spiral

out from a source at the origin.

The two concepts of stability are independent; that is, there are examples

of equilibria that are attracting but not stable and equilibria that are stable but

not attracting. The equilibrium

v ⫽ 0 in (7.21) is asymptotically stable, therefore

stable in both senses. In (7.17) and (7.22), the origin is unstable and not attracting.

In Example 7.7, the origin is stable (take N

⫽ N) but not attracting. For a

linear system, the stability of the equilibrium at the origin is determined by the

eigenvalues of the matrix A. If A has at least one eigenvalue with positive real

part, at least one with negative real part, and no eigenvalues with real part zero,

then 0 is called a saddle. In (7.14) and (7.16), the origin is a saddle. Note that

saddles are unstable.

E XAMPLE 7.11

The origin of the system

x ⫽ x ⫺ 2y

y ⫽ 5x ⫺ y (7.23)

is a stable equilibrium with eigenvalues ⫾3i. The solutions are ellipses centered

at the origin, as shown in Figure 7.9(b). This example shows why the deﬁnition

of Lyapunov stability needs two neighborhoods: In order to have solutions stay

291

D IFFERENTIAL E QUATIONS

within a neighborhood whose radius is the larger axis of an ellipse, initial con-

ditions must be restricted to a neighborhood whose radius is no larger than the

smaller axis of the solution.

✎ E XERCISE T7.4

Find the equations of the ellipses in Figure 7.9(b). They are given in para-

metric form by the solutions x(t)andy(t) of (7.23), which are linear com-

binations of cos 3t and sin 3t.

Criteria for stability of a linear system are given by Theorem 7.12.

Theorem 7.12 Let A be an n ⫻ n matrix, and consider the equation ˙v ⫽ Av .

If the real parts of all eigenvalues of A are negative, then the equilibrium

v ⫽ 0 is

globally asymptotically stable. If A has n distinct eigenvalues and if the real parts of all

eigenvalues of A are nonpositive, then

v ⫽ 0 is stable.

✎ E XERCISE T7.5

Let

x ⫽ y

y ⫽ 0. (7.24)

Show that (x(t),y(t)) ⫽ (at, a), a ⫽ 0, is an unbounded solution of (7.24).

Therefore

v ⫽ 0 is an unstable equilibrium. Explain why this example does

not contradict Theorem 7.12.

✎ E XERCISE T7.6

Determine the possible phase plane diagrams for two-dimensional linear

systems with at least one eigenvalue equal to 0.

Thus far, we have only shown ﬁgures of one- and two-dimensional phase

planes. The phase portraits of higher dimensional linear systems can be obtained

by determining on which subspaces the equilibrium 0 is stable, asymptotically

stable, or unstable.

292

7.3 LINEAR D IFFERENTIAL E QUATIONS IN M ORE THAN O NE D IMENSION

E XAMPLE 7.13

Let

x ⫽ 5x ⫹ y ⫹ z

y ⫽⫺2y ⫺ 3z

z ⫽ 3y ⫺ 2z. (7.25)

Verify that the eigenvalues are 5 and ⫺2 ⫾ 3i. The eigenspace for the eigenvalue

5isthex-axis. The phase space for this system is shown in Figure 7.11. The (y, z)

coordinates of trajectories move toward (y, z) ⫽ (0, 0). All trajectories except for

those in the plane shown move away from origin 0 ⫽ (0, 0, 0) along the x-axis,

and satisfy |x(t)| →

⬁

while y(t),z(t) → 0. Trajectories in the plane with normal

vector (1, 5 29, 2 29) spiral in to the origin. This “eigenplane” is the stable

manifold of the saddle; the x-axis is the unstable manifold. On the other hand, if

the 5 is replaced by a negative number in (7.25), the origin 0 would be globally

asymptotically stable.

If the number of linearly independent eigenvectors associated with a given

eigenvalue

␭

is fewer than the multiplicity of

␭

as a root of the characteristic

equation, then determination of the “generalized eigenspace” associated with

␭

is somewhat more complicated. We refer the reader to (Hirsch and Smale, 1974)

for a complete treatment of this subject.

Figure 7.11 A three-dimensional phase portrait.

In Example 7.13, the origin (0, 0, 0) is a saddle equilibrium. Trajectories whose

initial values lie in the plane move toward the origin, and all others spiral away

along the x-axis.

293

D IFFERENTIAL E QUATIONS

➮ COMPUTER EXPERIMENT 7.2

Although linear systems can be solved with linear algebra, most nonlinear

systems do not yield to analytic methods. For example, for the equation

x ⫽ y ⫺ x

y ⫽⫺x, (7.26)

obtained by adding a single nonlinear term to (7.18), we are reduced to numerical

approximation methods, summarized in Appendix B. Plot solution curves of

(7.26) near the origin. According to this evidence, do you expect that the origin

is asymptotically stable? Lyapunov stable?

7.4 NONLINEAR SYSTEMS

In the ﬁrst portion of this book, we used maps to model deterministic physical

processes. We speciﬁed a map and the present state, and then as long as the map

was well-deﬁned, it told us unequivocally what happens for all future time. Now

we want to use differential equations for the same purpose.

With differential equations, there are a few technicalities we need to con-

sider. First, we have seen already that solutions to an initial value problem may

blow up in ﬁnite time, and therefore not exist for all time. This happens for (7.10),

for example. It is possible, both for differential equations and maps, for solutions

to tend to inﬁnity, but exist for all time in the process. But blow-up in ﬁnite time

is different, and there is no analogue of this behavior for continuous maps.

Second, without any restrictions on the equations, an initial value problem

may have more than one solution. This goes against the spirit of determinism.

A good model should specify the future unambiguously, given the rule and the

present state. But the initial value problem

x ⫽



x(0) ⫽ 0 (7.27)

has two solutions, x(t) ⫽ 0andx(t) ⫽ t

 4. This does not make for a good model

of a dynamical process.

Third, the utility of a model to give information about the dynamical process

depends on the fact that the solution of the initial value problem does not depend

294

7.4 NONLINEAR S YSTEMS

too sensitively on the initial condition, at least at short time scales. In particular,

for a ﬁxed differential equation and two different initial values, we would like to

know that the closer the two initial values are, the closer the solutions are for

small t. This is called continuous dependence on initial conditions. For large t,

we can’t expect them to stay close—they may diverge toward opposite corners

of phase space. Sensitivity at large t is called sensitive dependence on initial

conditions.

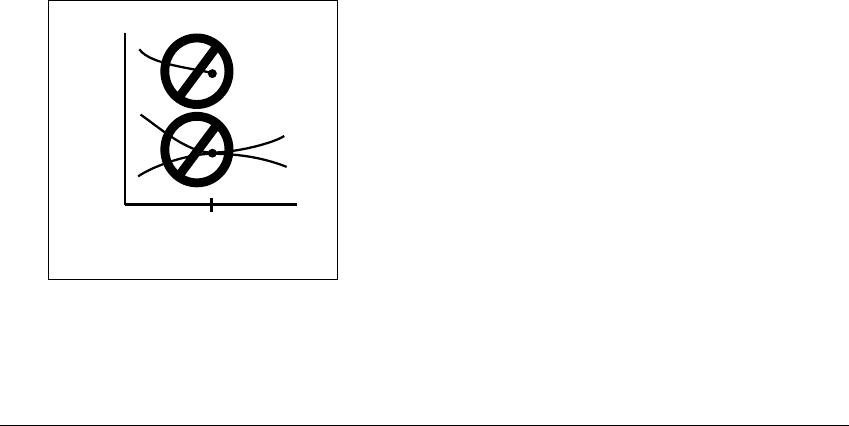
Except for blow-up in ﬁnite time, these problems disappear under mild

restrictions on the differential equation. We now present theorems on existence

and uniqueness (Theorem 7.14) and continuous dependence on initial conditions

(Theorem 7.16). Proofs of these theorems can be found in standard differential

equations texts. Figure 7.12 shows two types of solution behavior which are ruled

out.

Consider the ﬁrst-order system

⫽ f

,...,x

)

⫽ f

,...,x

). (7.28)

We denote this n-dimensional system of ﬁrst-order ordinary differential equations

˙v ⫽ f(v), (7.29)

where v ⫽ (x

,...,x

) is a vector.

Figure 7.12 Solutions that are outlawed by the existence and uniqueness

theorem.

Solutions cannot suddenly stop at t

, and there cannot be two solutions through a

single initial condition.

295

D IFFERENTIAL E QUATIONS

Theorem 7.14 Existence and Uniqueness. Consider the ﬁrst-order differen-

tial equation (7.29) where both f and its ﬁrst partial derivatives with respect to v are

continuous on an open set U. Then for any real number t

and real vector v

,there

is an open interval containing t

, on which there exists a solution satisfying the initial

condition v(t

) ⫽ v

, and this solution is unique.

Deﬁnition 7.15 Let U be an open set in ⺢

. A function f on ⺢

is said

to be Lipschitz on U if there exists a constant L such that

|f(v) ⫺ f(w)| ⱕ L|v ⫺ w|,

for all v, w in U. The constant L is called a Lipschitz constant for f.

If f has bounded ﬁrst partial derivatives in U,thenf is Lipschitz. For

example, for the one-dimensional case, f(x) ⫽ sin x has Lipschitz constant L ⫽ 1.

This follows from the Mean Value Theorem and the fact that f



(x) ⫽ cos x.

✎ E XERCISE T7.7

The general two-dimensional linear equation is

v ⫽ Av where

A ⫽





Find a Lipschitz constant for the function Av on ⺢

in terms of a, b, c,

and d.

Two neighboring solutions to the same differential equation can separate

from each other at a rate no greater than e

,whereL is the Lipschitz constant of

the differential equation. The Gronwall inequality, illustrated in Figure 7.13, is

the basis of continuity of the ﬂow as a function of the initial condition.

Theorem 7.16 Continuous dependence on initial conditions. Let f be de-

ﬁned on the open set U in ⺢

, and assume that f has Lipschitz constant L in the variables

v on U. Let v(t) and w(t) be solutions of (7.29), and let [t

] be a subset of the

domains of both solutions. Then

|v(t) ⫺ w(t)| ⱕ |v(t

) ⫺ w(t

)|e

L(t⫺t

)

for all t in [t

296