Аракелян А.К., Афанасьев А.А. Вентильные электрические машины и регулируемый электропривод. Книга 2

Подождите немного. Документ загружается.

301

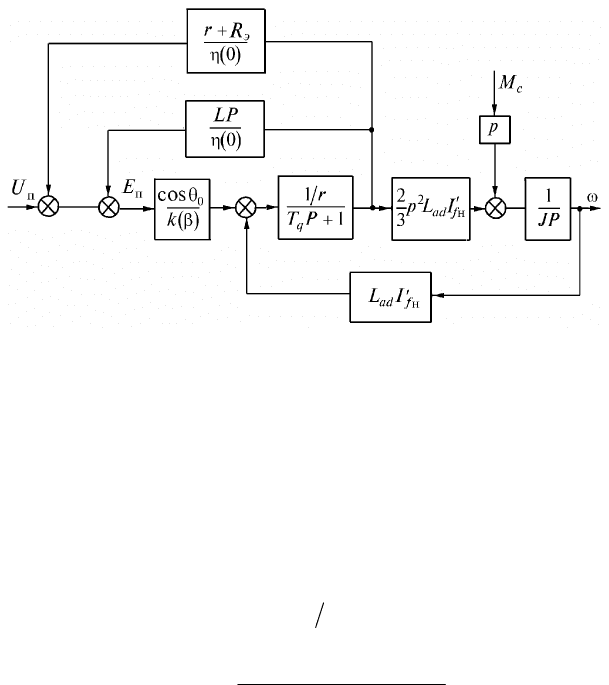
Рис. 12.2. Упрощенная структурная схема вентильного двигателя:

—

эквивалентное сопротивление, учитывающее сопротивление

сглаживающего дросселя и коммутационного явления в инверторе,



—

приведенный к обмотке статора номинальный ток возбужде-

ния двигателя

Передаточная функция этой структурной схемы, напри-

мер, по управляющему воздействию







U P

 0 для прира-

щения скорости определится из (12.6):













 

p U P W p



, (12.7)

где

 

W P

b p b

a p a p a p a

1 2

3 4





  

;









a JrT T Kr L

q q

2 0  cos ;













a Jr Kr T T R r L

q q

2 2 0   

э 0 0

;cos cos 

302

 





 





a r JrK J R r K p L I T

ad f q

2 2 2

2 0 2 3 0    

э 0

cos ;













a L I Kr R r

ad f

2 2

3 0  

э 0

;cos 





b r L I r T

f q

3 0

; cos 





b r L I

2 2

3 0  cos .

Анализ уравнения (12.7) показывает, что коэффициенты

характеристического уравнения при использовании инверто-

ров тока (со сравнительно большой индуктивностью во вход-

ной цепи) могут иметь различные знаки, что при отсутствии

регуляторов возбуждения или напряжения (или и того и дру-

гого) обусловит неустойчивую работу [27].

В целях сопоставления ожидаемых результатов при ис-

следовании модели ВД по рис. 12.2 с синхронными двигате-

лями соответственно 2,0 и 4000 кВт (см. приложение 12.1)

при различных способах синхронизации инвертора и различ-

ных величинах сопротивлений входной цепи были рассчита-

ны коэффициенты характеристического уравнения (12.7) и

операторного коэффициента управляющего воздействия, ко-

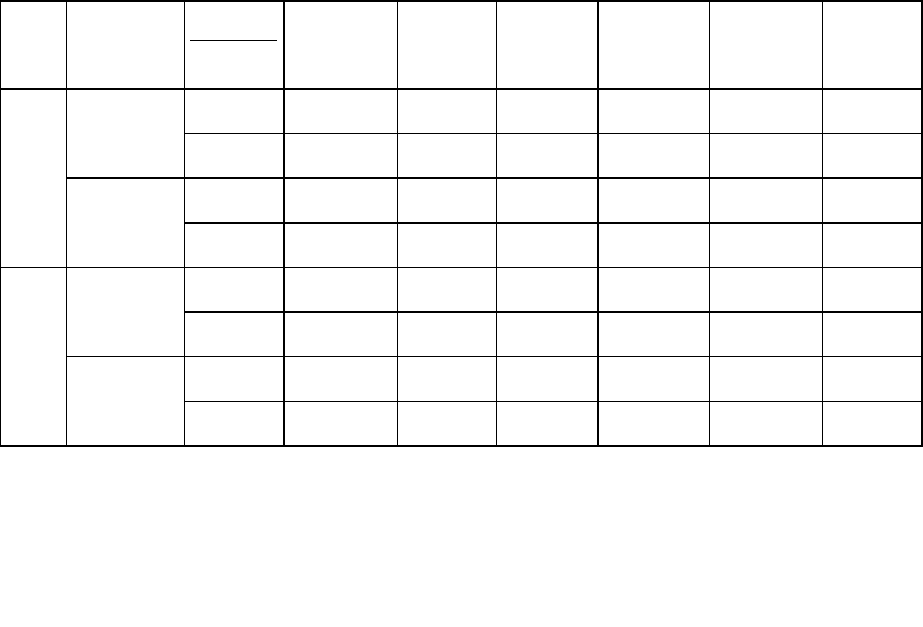
торые сведены в табл. 12.1.

Данные таблицы свидетельствуют о существенном влия-

нии на степень устойчивости ВД индуктивности сглаживаю-

щего дросселя и суммарного активного сопротивления цепи

постоянного тока, частично учитывающего влияние комму-

тационного процесса в системе инвертор—двигатель.

„Таким образом, по линеаризованным уравнениям син-

хронной машины получены сравнительно точные передаточ-

ные функции ВД, по которым можно произвести построение

частотных характеристик ВД при синтезе САР. Упрощение

структуры ВД позволяет снизить порядок характеристическо-

го уравнения без существенного ущерба динамическим свой-

ствам, что делает доступным приближенный анализ и синтез

САР с ВД в процессе поиска структур регуляторов.

При расчетах коэффициентов характеристического уравне-

ния для ВД с тактовой синхронизацией инвертора по положе-

нию ротора приняты:

0 968 , ,

1 37 , , tg

  0 577, .

При синхронизации по напряжению соответственно при-

няты:

 0 907, , cos ,

 0 866 .

303

Таблица 12.1

Р,

кВт

Способ

синхро-

низации

инвертора

Коэффи-

циенты



Гн

кг

Гн

кг

—1

Гн

кг

—2

Гн

кг

—3

Гн

кг

—3

Гн

кг

—4



 const

—7,0

—4

—9,0

-3

—4,5 64,2 76,5

—2

2,0

R r



—7,0

—4

—3

—4,17 201 76,5

—2



 const

—85,7

-6

—6,0

-3

—44,4

-1

31,9 67

—2

10,4

R r



—85,7

-6

17,8

-3

—41,5

-1

16,5 67

—2

10,4



 const

—87,3

-4

2,3

—1

—42,2 98 12,5

—2

4000

R r



—87,3

-4

1,1 —35,4 403 12,5

—2



 const

—9,5

—6

—4,6

-5

—150,4 2,57 41,5

—2

R r



—9,5

—6

7,4

—4

—150,4 12,5 41,5

—2

303

304

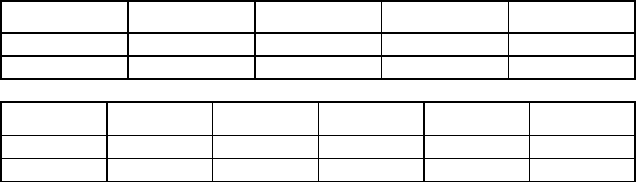
Приложение 12.1

кВт

, В

, А

Гн

2,0 200 7,2 0,052 0,026

4000 6000 439 0,0056 0,0056

Ом

, с

кг

, Гн

, Ом

0,402 0,064 0,139 2 0,12 0,2

0,042 0,13 69,5 1 0,031 0,02

12.2. Частотные характеристики вентильного двигателя

На основе полученной в 12.1 линеаризованной системы

уравнений ВД исследуются с помощью расчетных частотных

характеристик влияния отдельных параметров ВД с датчиком

положения ротора на его конструктивные особенности и ди-

намические свойства.

При математическом описании связей первых гармоник

переменных синхронного двигателя в форме уравнений Пар-

ка-Горева приняты общеизвестные допущения [13]. Что ка-

сается вентильного коллектора (инвертора тока), то приня-

тый метод непрерывной аппроксимации позволяет функцио-

нальную зависимость тока в звене, имеющую разрывы в точ-

ках переключения вентилей, представить гладкой состав-

ляющей входного (непрерывный) и выходного (синусоидаль-

ный) токов [543].

По структурным схемам (рис. 12.1) и исходным уравне-

ниям ВД для заданного рабочего (установившегося) режима,

определяемого выходными координатами (угловой скоростью



, углом нагрузки 

током обмотки якоря

и т.д.) и

переменными (напряжениями на зажимах якоря

п0

и об-

мотки возбуждения

моментом сопротивления на валу

), получена приведенная ниже система преобразованных

уравнений (12.3) линейного приближения для возмущенного

режима вентильного двигателя постоянного тока с датчиком

положения ротора [330]:

305





   

 

   

 

a p a p b b a p b i a p b i

a p b i a p b U a p b M

a p a p b b a p b i a p b i

a p b i a p b U a p b M

a p a p

kd f

kq c

kd f

kq c

12 11 12 13 13 14 14

15 15

16 16

17 17

22 21 22 23 23 24 24

25 25

26 26

27 27

       

      

       

      

 

   

   

   

   



;

 

b i a p i a p i a p a p M

a p a p i a p b i a p i a p U

a p M

a p a p i a p i a p b i a p a p M

a p a p b b a p b i a

kd f kq c

kd f kq f

kd f kq c

33 34 35 36 37

43 44 44 45

53 54 55 55

62 61 62 63 63 64

    

     



     

  

   

      



     

     

;

 

     

p b i

a p b i a p b U a p b M

kq c

 

      











65 65 66 66 67 67



   

(12.8)

где





, 



— приращения соответст-

венно угловой скорости, угла нагрузки, осевых состав-

ляющих тока якоря, тока возбуждения и угла коммутации

вентилей;



, 

— возмущающие воздействия соответ-

ственно по цепи якоря ВД, по цепи его обмотки возбуж-

дения и со стороны внешней механической нагрузки;

— постоянные коэффициенты, получаемые из на-

чальных условий (по установившемуся режиму), рассчи-

тываются по формулам, приведенным в приложении 12.2.

306

Из (12.8) следует, что собственные операторы координат





, i



a p b

 ... и операторы воздействия

внешнего возмущения по моменту

a p b

i i

7 7

 полиномы раз-

ной степени, что указывает на многоконтурные внутренние

структурные связи ВД.

Преобразование Лапласа для передаточной функции лю-

бой из указанных выше координат получается на основе сис-

темы (12.8), представленной матричным уравнением

 

 





 









   

 

   

 

   

W P

i p

U p A M p

A M p

U p A M p

A M p

U p A M p

n k

f c







































 



 



 

, (12.9)

где

A b p b

i i i

7 7 7

  ,



;





W p

n k



— матрица коэффициентов уравнения (12.8),



Пользуясь методом суперпозиции, определим передаточ-

ные функции по скорости при возмущениях вентильного

двигателя по независимым каналам управления и возмуще-

нии по нагрузке. Получим:





 





 





U p

C p

W p

i j

n k

  



det

, ; , , ;1 1 2 6 (12.10)





 





 





U p

C p

W p

i j

n k

  



det

, ; ;1 4 (12.11)





 









 





M p

C p A p

W p

i j m

i jm

n k

   



det

, ; ... ; ,1 1 1 6 7 (12.12)

307

где

(р) —

алгебраические дополнения первой строки при-

соединенной матрицы;

(р)

— операторные воздействия при







M p

;





det

W p

n k



— определитель исходной матрицы





W p

n k



или характеристическое уравнение вентильного двигате-

ля.

Аналогичным способом могут быть получены передаточ-

ные функции по другим координатам ВД и по соответст-

вующему возмущению.

В случае одновременного воздействия всех возмущений

на основании (12.10)—(12.12) получаем

 





























 



  

C p U p C p U p C p A p M p

W p

ij ij f i jm c

n k



 



det

С помощью этих расчетных уравнений построены час-

тотные характеристики для вентильного двигателя мощно-

стью 2,35 кВт, с номинальными: напряжением 200 В, током

5 А, угловой скоростью 628 рад/с (номинальная частота 100

Гц), имеющего следующие

параметры:

 0 0157, Гн;

 0 0086, Гн;

 0 0178, Гн;

 0 0126, Гн;



 0 00414, Гн;



 0 00677, Гн;



 0 0052, Гн;   

L L

a q

0 006, Гн;

 2 0, Ом;

 01, Ом;

 0 2, Ом;

 2 2, Ом;

 011, Гн;

 0 28, Ом;

 0 456, кгм

;

сх

 1 65, ;  

52 А;   56 эл. гр.

и работающего в установившемся режиме с переменными:



536 5 , рад/с; 

53 эл. гр.; 

44 2 , эл. гр.;

1 0

22189 , В;

1 0

4 94 , А; 

47 2 , эл. гр.;



 8,78 эл. гр.; 

6 эл.гр.

308





W p

n k





        

       

  

   

0046 18 038 133765 0078 472 0078 472 003 4022 067 110

0029 047 047 307198 0009 539 0009 539 0005 03 03 784

00018 0 0016 02 00092 00092 0034

00018 0 00092 0013 01

, , , , , . , , , ,

, , , , , , , , , , , ,

, , , , , ,

, , , ,

p p p p p p

p p p p p

p p p

00012 0034

0002 0 000067 000067 00165 22 000108

0026 14 048 51158 0009 471 0009 471 0017 918 03 2679

, ,

, , , , , ,

, , , , , , , , , ,

p p

p p p p p

p p p p p p

   

       

а коэффициенты

 

A p

p p p



    

 

0 2 61 5 013 2 08 0 08

0 008 0 09 012 61 5

, , , , ,

, , , ,

. (12.13)

Из решения уравнения (12.9) получены передаточные

функции (12.10)—(12.12) в явном виде. Построенные по этим

передаточным функциям логарифмические амплитудно-

частотные





 и фазочастотные





  характеристики ВД

приведены на рис. (12.3), где показаны также запасы по ам-

плитуде





 и по фазе





  при возмущении по возбужде-

нию.

Для определения степени влияния .демпферных обмоток

на динамические свойства двигателя и электропривода в

целом были рассчитаны частотные характеристики для слу-

чая отсутствия демпферных обмоток на роторе синхронной

машины. С этой целью в формулах (12.8) и (12.9) исключа-

лись члены уравнений, зависящие от 

и 

, то есть в

матрице коэффициентов вычеркивались третий и пятый

столбцы и строчки, а в строке коэффициентов





A p

третий и пятый коэффициенты.

При этом пренебрегали изменением эквивалентного ак-

тивного сопротивления вентильного двигателя без демпфер-

ной обмотки по сравнению с эквивалентным активным со-

противлением двигателя с демпферными обмотками, так как

при расчетной скорости вращения поля двигателя влияние

его на величины коэффициентов незначительно [38].

309

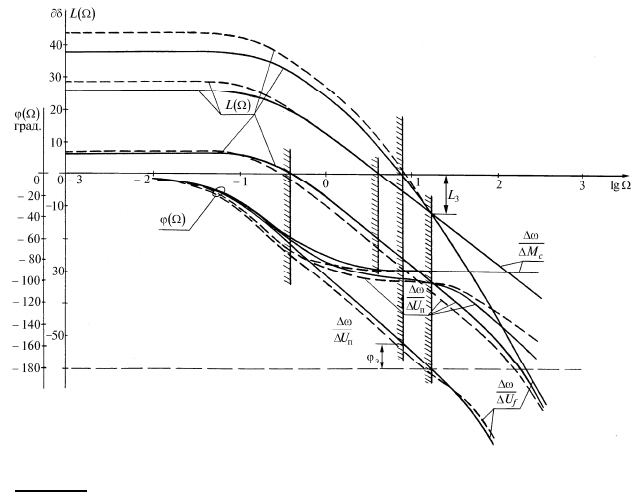
Рис. 12.3. Частотные характеристики вентильного двигателя:

с учетом и без учета демпферных обмоток;

- - - - - при изменении воздушного зазора синхронной машины

Для ВД без демпферных обмоток также были получены

передаточные функции (12.10)—(12.12), в которых характери-

стическое уравнение





det

W p

n k



понижается на два порядка.

Расчет для этого случая показал полное совпадение частот-

ных характеристик вентильного двигателя с демпферными

обмотками с характеристикой вентильного двигателя без

демпферных обмоток (рис. 12.3 — непрерывные линии).

Исследуя возможность понижения порядка характеристи-

ческого уравнения вентильного двигателя без ущерба точно-

сти, пренебрегаем последней строчкой и столбцом уравне-

ний (12.8) и (12.9), то есть уравнением, связывающим угол

коммутации инвертора



от возмущения. При этом полу-

чаются передаточные функции с характеристическим урав-

нением третьего порядка. На рис. 12.4 пунктирными линия-

ми показаны частотные характеристики для этого случая.

310

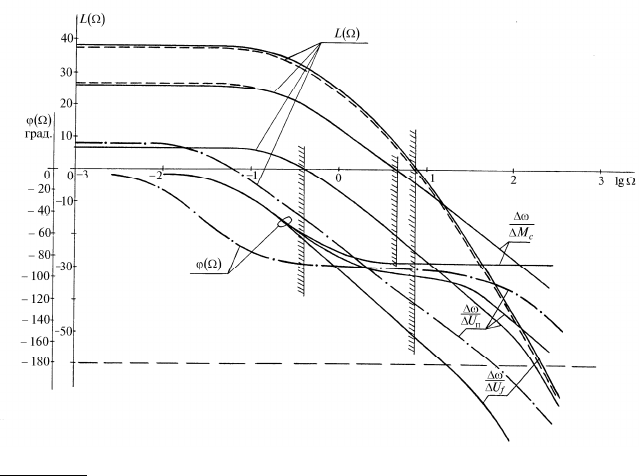
Рис. 12.4. Частотные характеристики вентильного двигателя:

с учетом и без учета демпферных обмоток;

- - - - - - - без учета коммутации и демпферных обмоток;

– · – · – · –

без учета угла коммутации, демпферных обмоток и пре-

небрежении влиянием по оси q

Попытка упрощения расчетных формул частотных характе-

ристик путем пренебрежения индуктивностями по оси

пока-

зала (рис. 12.4 — штрихпунктирные линии) существенное отли-

чие последних от ранее рассмотренных характеристик.

Для оценки степени влияния воздушного зазора между

ротором и статором синхронной электрической машины,

работающей по схеме ВД, на частотные характеристики —

расчетный воздушный зазор машины был уменьшен в 2 раза.

При этом для получения того же статического коэффициента

усиления машины по каналу управления напряжением ток

возбуждения машины был уменьшен также в 2 раза.

Расчеты показали хорошее совпадение средних и высоко-

частотных областей частотных характеристик (рис. 12.3 —

пунктирные линии). Низкочастотные области имеют отличие

от характеристик с нормальным воздушным зазором из-за

изменения статического коэффициента усиления по этим

каналам.