Аренс Э.А. Аудит

Подождите немного. Документ загружается.

ВЫБОРОЧНОЕ ИССЛЕДОВАНИЕ ДЛЯ ПРОВЕРОК СТА ТЕЙ БАЛАНСА 439

Рис. 14.2. Взаимосвязь между факторами, связанными с ARIA,

и нужным объемом монетарной выборки

ФАКТОР,

ВЛИЯЮЩИЙ НА

ARIA

ПРИМЕР

ВЛИЯНИЕ

НА ARIA

ВЛИЯНИЕ

НА ОБЪЕМ

МОНЕТАРНОЙ

ВЫБОРКИ

Эффективность

в нутр нхозяйствен-

ных контрольных

моментов (риск

конт_роля)

Контрольные момен-

ты эффективны

(уменьшенный риск

контроля)

Увеличение

Уменьшение

Приемлемый ауди-

торский риск

Вероятность банк-

ротства высока

(уменьшенный при-

емлемый аудитор-

ский риск)

Уменьшение

Увеличение

Аналитические про-

цедуры

По аналитическим

процедурам не выяв-

лено вероятных оши-

бок

Увеличение

Уменьшение

ОЦЕНИТЕ НОРМУ ОШИБОК В СОВОКУПНОСТИ. Монетарная вы-

борка (долларовое выборочное исследование) применяется, когда аудитор

считает, что существенные ошибки в совокупности маловероятны. Если

оцененная норма отклонений вероятна даже на 2 или 3%, то обычно

аудиторы используют другой метод статистического выборочного иссле-

дования или нестатистическое выборочное исследование. Это обусловлено

тем, что монетарная выборка может быть неэффективной при средней

или большой норме ошибок. Таким образом, при монетарной выборке ти-

пичными являются оценки нормы ошибок, равные 0 или 1%.

ОПРЕДЕЛИТЕ НАЧАЛЬНЫЙ ОБЪЕМ ВЫБОРКИ. Подходящий объем

монетарной выборки легко вычислить. Однако это легче объяснить после

того, как будет показана методология определения результатов. Таким

образом, рассмотрение это вопроса откладывается до конца главы.

ПОЛУЧИТЕ СЛУЧАЙНУЮ ВЫБОРКУ. Для получения монетарных

выборок сперва необходимо получить случайную выборку монетарных (в

нашем случае долларовых) единиц. Кроме того, нужно идентифицировать

единицы наблюдения, связанные с каждой монетарной (долларовой) еди-

ницей отбора. При этом монетарные единицы необходимы для расчета

статистических результатов, а единицы наблюдения - для тестов аудита.

Выборки монетарных (долларовых) единиц могут быть получены при

случайном или систематическом отборе множеством способов. Это видно

из примера совокупности дебиторской задолженности, включающей со-

вокупные суммы как долларовые единицы (табл. 14.1).

440 ВЫБОРОЧНОЕИССЛЕДОВАНИЕДЛЯ'ПРОВЕРОК СТАТЕЙБАЛАНСА

Таблица 14.1

Совокупность дебиторской задолженности

ЕДИНИЦА

УЧТЕННАЯ

СОВОКУПНАЯ

СОЮКУПНОСТИ

СУММА СУММА, ДОЛ.

{единица наблюдения)

дол.

(долларовая единица)

357

2 1281

1638

3 60

1698

573 2271

5 691

2962

143 3105

1425 4530

8 278

4808

942 5750

826

6576

11 404

6980

7376

1. Таблица случайных чисел - совокупные суммы. Предположим, что

аудитор хочет сформировать случайную выборку из четырех единиц (для

процедуры подтверждения) с использованием монетарной выборки. В ка-

честве единицы отбора определен доллар, объем совокупности равен 7376

и из таблицы случайных чисел отбираются 4 цифры; аудитор использует

первые четыре цифры в таблице случайных чисел (табл. 12.2) с началь-

ной точкой в строке 1002, столбец 4. Тогда используемые случайные чис-

ла (представляющие отобранные случайным путем долларовые величины)

будут 6586, 1756, 850 и 6499. СЬвокуттность единиц наблюдения, вклю-

чающих эти отобранные величины, определяется по столбцу совокупных

сумм. Это единицы 11 (содержащая долларовые величины с 6577 по

6980), 4 (с 1699 по 2271), 2 (с 358 по 1638) и 10 (с 5571 по 6576). Они

и будут подвергнуты аудиту, а результат для каждой единицы наблю-

дения будет распространен на сумму, которую она содержит.

Статистические методы для оценки в монетарных выборках, допуска-

ют включение в выборку единиц наблюдения более одного раза. Так, в

предыдущем примере, если случайные числа равны 6586, 1756, 856, 6599,

то элементами выборки будут 11, 4, 2 и 11. По ним аудитор и разошлет

материалы для подтверждения, т. е. элемент 11 будет статистически рас-

сматриваться как два элемента, а выборка будет состоять из четырех еди-

ниц, по числу включенных четырех монетарных единиц.

ВЫБОРОЧНОЕ ИСХЖаОВАНИЕЛДЯПРОВЕРОКСТАТЕЙБАЛАНСА 441

2. Систематическое выборочное исследование. Процедуры системати-

ческого отбора для монетарных выборок очень похожи на процедуры слу-

чайного отбора. При случайном отборе единица выборки - это отдельная

долларовая величина, а совокупность - это отраженная в учете итоговая

сумма. Интервал отбора определяется делением объема совокупности на

требуемый объем выборки. В предыдущем примере интервал равен 1844

(7376 : 4). Начальная точка (между 0 и 1843) выбирается случайно по

таблице случайных чисел (предположим, что это 921) и к ней прибав-

ляется интервал. Отобранными монетарными единицами, следовательно,

будут 921; 2765 (921 + 1844); 4609; и 6453. Элементы совасупности: 2,

5, 8 и 10.

Систематический отбор для монетарной выборки потенциально не-

объективен, как уже говорилось в гл. 12, но вероятность ошибки здесь

меньше, поскольку отбираются случайные долларовые величины, а не

случайные единицы наблюдения. Маловероятно, что компания намеренно

или ненамеренно расположит элементы совокупности так, что это будет

влиять на случайность распределения ошибок среди различных долларо-

вых величин. Некоторые аудиторские фирмы для получения монетарной

выборки прибегают только к систематическому отбору.

3. Компьютерная техника. Для генерирования выборок и определе-

ния чисел отобранных единиц двумя рассмотренными методами могут ис-

пользоваться компьютерные программы. При их помощи аудиторы

получают монетарные выборки (конечно, если данные по совокупности

представлены в машиночитаемой форме).

Проблемы, связанные с получением монетарных выборок. У элементов

совокупности, имеющих в учете нулевое сальдо, нет шансов быть полу-

ченными в монетарной выборке, даже несмотря на то, что в них

тоже может быть ошибка. Точно так же и небольшие сальдо, которые

существенно занижены, вряд ли попадут в выборку. Но аудитор решит

эту проблему, выполнив проверки по существу для нулевых и небольших

сальдо.

Другая проблема - неспособность включить пассивные остатки (такие,

как кредитовые сальдо по дебиторской задрлжеююсти) в монетарную вы-

борку. Но их можно игнорировать в монетарной выборке и проверять

другими средствами. В качестве альтернативы допустимо рассматривать

их как активные сальдо и прибавлять к итоговой тестируемой сумме, но

это затрудняет процесс оценки.

ВЫПОЛНИТЕ ПРОЦЕДУРЫ АУДИТА. Чтобы выполнить процедуры

проверки, аудитор сначала получает выборку долларовых величин и

идентифицирует единицы наблюдения, содержащие монетарные единицы

(при этом он использует один из методов, описанных выше). Затем ауди-

тор применяет подходящие процедуры, чтобы определить, содержит ли

каждая единица наблюдения ошибку. Например, для подтверждения де-

биторской задолженности аудитор посылает по почте выборку подтвер-

442 ВЫБОРОЧНОЕ ИССЛЕДОВАНИЕДЛЯПРШЕРОК СТАТЕЙ БАЛАНСА

ждений так, как это описано в гл. 13, и определяет сумму ошибок в каж-

дом подтвержденном счете. В тех случаях, когда ответы не получены,

для определения ошибки он выполняет альтернативные процедуры.

РАСПРОСТРАНИТЕ РЕЗУЛЬТАТЫ ВЫБОРКИ НА СОВОКУП-

НОСТЬ. Как говорилось в начале главы, аудитор должен предсказать

ошибки совокупности исходя из результатов выборки и определить вы-

борочную ошибку. При распространении результатов выборки на сово-

купность в монетарной выборке следует иметь в виду четыре заслужи-

вающих внимания аспекта.

• Для расчета результатов используются таблицы качественного выбо-

рочного исследования. Можно взять таблицу (такую, как на рис. 12.9)

для оценки выборочных результатов в монетарной выборке. Приемле-

мый риск максимального доверия заменяется в таблице риском оши-

бочного принятия, а действительное число отклонений - действитель-

ным числом ошибок.

• Качественные результаты могут быть превращены в стоимостные (дол-

ларовые). Монетарная выборка помогает определить ошибку в совокуп-

ности, а не процент единиц совокупности, содержащих ошибку.

• Аудитор должен сделать предположение о проценте ошибки для каж-

дой содержащей ошибку единицы. Это предположение позволит ауди-

тору использовать таблицы качественного выборочного исследования

для оценки монетарных ошибок.

• Статистические результаты в монетарной выборке называются преде-

лами ошибки. Вычисляются оба предела ошибки - верхний и нижний.

РАСПРОСТРАНЕНИЕ ПРИ ОТСУТСТВИИ ОШИБОК. Предполо-

жим, аудитор подтверждает правильность совокупной суммы деби-

торской задолженности на монетарной основе. Совокупность составляет

1 200 ООО дол. Проведена выборка, получены данные и выполнены ауди-

торские процедуры для ста подтверждений. В результате аудита в вы-

борке не обнаружено ошибок. Аудитор хочет определить оценки ошибок

завышения и занижения в этой задолженности (в счетах дебиторов), ко-

торые являются верхней границей ошибки и нижней границей ошибки.

Используя таблицу выборочного исследования (табл. 12.9) и полагая, что

риск ошибочного принятия равен 5%, аудитор найдет верхний и нижний

пределы ошибки на пересечении строки, где дан объем выборки (100),

и столбца с данными о действительном количестве ошибок (0), как при

качественном выборочном исследовании. Ошибка равна 3%. Она назы-

вается процентным пределом ошибки. Таким образом, верхний процен-

тный предел ошибки и нижний процентный предел ошибки равны 3.

Исходя из результатов исследования выборки и пределов ошибки ауди-

тор может сделать вывод о том, что неточно указаны не более 3% мо-

нетарных (долларовых) единиц. Однако между результатами монетарной

выборки и качественного выборочного исследования существует важное

различие. В тестах контрольных моментов отклонение или существует,

ВЫБОРОЧНОЕ ИССЛЕДОВАНИЕ ДЛЯ ПРОВЕРОК СТА ТЕЙ БАЛАНСА 443

или не существует. А в монетарных тестах ошибка может изменяться

в каждой долларовой величине от одного цента до доллара (для зани-

жений ошибка может быть больше одного доллара).

Аудитор должен сделать предположение о средней процентной доле

ошибки для единиц совокупности, содержащих ошибку. Это предпо-

ложение значительно влияет на пределы ошибки. Чтобы показать на при-

мере обоснование предположения о процентной доле ошибки, рассмотрим

3 случая: 1) и завышения, и занижения равны 100-процентным ошиб-

кам; 2) завышения и занижения равны 10-процентным ошибкам; 3) за-

вышения равны 20-процентным ошибкам, а занижения -

200-процентным ошибкам.

Предположение 1. Ошибки завышения равны 100%; ошибки заниже-

ния - 100%; пределы ошибки при 5 процентном риске ошибочного

принятия будут.

верхний - 1 200 000 дол. * 3% * 1 - 36 000 дол.;

нижний - 1 200 000 дол. * 3% * 1 - 36 000 дол.

Предположение заключается в том, что в среднем единицы совокуп-

ности, содержащие ошибку, будут неточно указаны на полную монетар-

ную сумму учтенной величины. Поскольку предел ошибки равен 3%,

монетарное значение ошибки, вероятно, не превысит 36 000 дол. Если

все ошибки - завышения, то завышение будет на 36 000 дол. Если все

ошибки - занижения, то выявится занижение на 36 000 дол.

Предположение о 100% ошибок крайне консервативно, особенно для

завышений. Допустим, что действительная норма ошибок совокупности

3%. До того, как 36 000 дол. будут правильно отражать верхний предел

ошибки, придется ввести два условия:

• Все ошибки должны быть завышениями. Компенсационные ошибки

будут уменьшать величину завышения.

• Все элементы совокупности, содержащие ошибки, должны быть не-

верны на 100%. Например, не может быть ошибки такой, как в чеке,

выписанном на 262 дол. и учтенном на 226 дол.

При определении пределов ошибки завышения и занижения на

36 000 дол. аудитор не вычислял оценку и выборочную ошибку, как

обсуждалось ранее в этой главе. Это обусловлено тем, что использованные

таблицы включали точечную оценку и выборочную ошибку для нахож-

дения данной верхней нормы ошибки.

Таким образом, несмотря на то, что для монетарной выборки точечная

и выборочная ошибки не вычисляются, они учитываются при расчете

пределов ошибки.

Предположение 2. Ошибки завышения, как и ошибки занижения, равны

10%, пределы ошибки при 5% риске будут

верхний - 1 200 000 дол. х 3% * 0,1 - 3 600 дол.;

нижний * 1 200 000 дол. х 3% х 0,1 - 3 600 дол.

444 ВЫБОРО ИНОЕ ИССЛКДОВЛННЕДЛЯ ПРОВЕРОК СТА ТЕЙ БАЛАНСА

Предположение заключается в том, что в среднем элементы, со-

держащие ошибку, неверны не более, чем на 10%. Если все элементы

ошибочны в одном направлении, пределы ошибки будут +3600 дол. и

-3600 дол. Изменение 100% ошибок на 10% значительно влияет на пре-

делы ошибки.

Предположение 3. Ошибки завышения равны 20%, ошибки заниже-

ния - 200%, пределы ошибки при 5% риске будут:

верхний - 1 200 000 дол. х 3% х 0,2 - 7 200 дол.;

нижний - 1 200 000 дол. х 3% х 2,0 - 72 000 дол.

Оправдание для большего процентного отношения завышений - боль-

шая возможная процентная ошибка. Например, учтены счета дебиторов

при 20%, которые следовало учесть при 200%, занижены на 900%,

в то время как учтенные при 200%, вместо 20%, завышены на 90%

[(200 - 20)] : 200.

Единицы, содержащие большие ошибки занижения, могут быть учтены

как небольшие величины благодаря этим ошибкам. Следствие этого -

применение статистического аппарата монетарной выборки приводит к

тому, что лишь небольшое количество таких ошибок имеет шанс быть

по-лученным в выборке. Из-за этого некоторые аудиторы проводят до-

полнительную выборку небольших единиц, когда ошибкам занижения

уделяется в ходе аудита повышенное внимание.

Предположение приемлемого процента ошибки. Решение об общем про-

центе ошибки в элементах совокупности, содержащих ошибку, прини-

мает аудитор. Он должен установить эти соотношения в зависимости от

конкретных обстоятельств. При отсутствии убедительной информа-

ции об обратном большинство аудиторов считает желательным предпо-

лагать 100-процентную ошибку и для завышений, и для занижений.

Данный подход считается весьма консервативным, но обосновать такое

предположение легче, чем любое другое. Фактически причина, по кото-

рой верхняя и нижняя границы называются пределами ошибки в моне-

тарной выборке, а не максимальной вероятной ошибкой или

общепринятым статистическим термином "доверительный предел", за-

ключается в широком использовании этого консервативного предположе-

ния. В настоящей главе и в проблемных публикациях обсуждается

предположение 100-процентной ошибки, если не указано иначе.

РАСПРОСТРАНЕНИЕ РЕЗУЛЬТАТОВ ВЫБОРКИ ПРИ ОБНАРУ-

ЖЕН1ТЫХ ОШИБКАХ. Этот раздел посвящен методу оценки, исполь-

зуемому, когда в выборке определены монетарные ошибки. Продолжая

прежний пример, внесем единственное изменение: предположение об

ошибках. Объем выборки остается равным 100, а отраженная в учете ве-

личина по-прежнему составляет 1 200 000 дел., но теперь в выборке пред-

полагается наличие пяти ошибок. Они показаны в табл. 14.2.

Применяются все те же 4 аспекта распространения результатов вы-

борки на совокупность, но они видоизменены:

ВЫМОРОЧНОЕ ИССЛЕДОВАНИЕ ДЛЯ ПРОВЕРОК СТА ТЕЙ БАЛАНСА 445

Таблица 142

Ошибки

ЗАКАЗ-

ЧИК

УЧТЕННЫЕ

СУММЫ

ПО СЧЕТАМ

ДЕБИТОРОВ,

ДОЛ.

ПРОВЕРЯЕМЬЕ

СУММЫ ПО

СЧЕТАМ

ДЕБИТОРОВ,

ДОЛ.

ОШИБКА

ОШИБКА,

ДЕЛЕННАЯ НА

УЧТЕННУЮ

СУММУ

2073

6200

6100

100

0,016

5111

12910

12000

910

0,07

5206

4322 4450

(128)

(0,03)

7642

23000 22995

0,0002

9816

8947 2947

6000 0,671

Наиболее консервативны предположения ошибок, равные 100 %• Для

завышения верхний предел ошибки равен 106 800 дол. (1 200 000

х 1,0 * 0,089), где величина 0,089 определена из таблицы качест-

венного выборочного исследования при 5-процентном риске для объема

выборки 100 с четырьмя ошибками.

• Там, где ошибки найдены, 100-процентное предположение для всех

ошибок не только исключительно консервативно, но также не со-

гласуется с ошибочными результатами. На практике принято считать

действительные ошибки выборки и распространять их на совокупность.

Так же принято и в нашей книге. Это предположение требует от ауди-

тора расчета для каждой ошибки среднего ее процента в содержащих

ошибку элементах выборки (ошибка, деленная на учтенную сумму де-

биторской задолженности) и затем распространения этого отношения

на всю совокупность. Расчет нормы для каждой ошибки показан в по-

следней колонке табл. 14.2. Предположение об ошибке еще будет не-

обходимо для нулевых ошибок вычисленных результатов. Например,

предположение о 100-процентной ошибке используется как для завы-

шения, так и для занижения.

• Аудитор должен работать со слоями расчетной верхней нормы от-

клонений из таблицы качественного выборочного исследования. При-

чина этого заключается в различных предположениях для каждого

• Ошибки завышения, и занижения рассматриваются раздельно. В при-

мере есть 4 ошибки завышения и одна ошибка занижения.

'Для каждой ошибки, включая нулевые, делаются разные предполо-

жения. Когда в выборке нет ошибок, требуется предпатожение о сред-

нем проценте ошибки для единиц совокупности, содержащих ошибку.

Пределы ошибки задавались для нескольких различных предположе-

ний. Теперь эти ошибки обнаружены, и информацию по выборке мож-

но использовать для определения пределов ошибки.

446 ВЫБОРОЧНОЕ ИССЛЕДОВАНИЕДЛЯ ПРОВЕРОК СТАТЕЙ БАЛАНСА

вида ошибок. Слои определяются путем расчета верхней нормы откло-

нений из таблицы для каждой ошибки с псхледующим расчетом по

каждому слою. Табл. 14.3 показывает эти слои.

• Предположение об ошибке должно ассоциироваться с каждым слоем.

Общепринятый метод установления соответствия предположения об

ошибке со слоем - соотнесение самых крупных процентов монетарных

ошибок с самыми большими слоями. Эта связь показана в табл. 14.4.

Например, самая крупная средняя ошибка была 0,671 у заказчика со

счетом на сумму 9816 дол. Эта ошибка соответствует фактору слоя 0,017,

самого крупного слоя, где были обнаружены ошибки. Для части верхнего

точечного предела, связанной со слоем нулевых ошибок, существует

предположение об ошибке 100%, что еще остается консервативным.

Таблица 14.3

ЧИСЛО

ОШИБОК

ВЕРХНИЙ ПРЕДЕЛ

ИЗТАБЛИЦЫ

УВЕЛИЧЕНИЕ ПРЕДЕЛА

ОШИБКИ (СПОИ)

0 0,030

С.030

0.047 0.017

0,062

0,015

0,076

0,014

4 0,089 0.013

Расчет верхнего и нижнего пределов ошибки показан в табл. 14.4.

Придерживаясь данной методики и следуя заданным предположе; гиям,

аудитор решает, что имеется 5-процентный риск того, что счета дебиторов

завышены не более, чем на 51 220 дол. и занижены не более, чем на

36 612 дол. Если предположения об ошибках менялись, пределы ошибки

тоже изменятся.

ПРОАНАЛИЗИРУЙТЕ ОШИБКИ. Как и в качественном выборочном

исследовании, аудитору необходима оценка сущности и причин ошибок.

Например, в подтверждениях дебиторской задолженности все ошибки

происходили из-за того, что клиент не отразил в учете возвращенные

товары. Аудитор должен определить, почему подобная ошибка так часто

встречается и могло ли это повлиять на объективность представления фи-

нансовой отчетности.

Важный момент анализа ошибок - решение вопроса о необходимости

изменить модель аудиторского риска. Если аудитор пришел к выводу, что

неудовлетворительное отражение в учете возвратов товара, о которых

шла речь выше, обусловлено несовершенством внутрихозяйственного кон-

троля, то он может сголкнуться с тем, что требуется заново оценить риск

контроля. Это в свою очередь, вероятно, заставит аудитора уменьшить

ARIA, что увеличит пределы ошибки в расчетах монетуihoh выборки,

ВЫБОРОЧНОЕ ИССЛЕДОВАНИЕ ДЛЯ ПРОВЕРОК СТА! ЕЙ БАЛАНСА 447

Таблица 14.4

Примеры расчета верхнего и нижнего пределов ошибки

ЧИСЛО

ОШИБОК

ВЕРХНИЙ

ПРЕДЕЛ •

УЧТЕННАЯ

ВЕЛИЧИНА,

ДОЛ.

ПРЕДПОЛО

ЖЕНИЕ ОБ

ОШИБКЕ

В ЕДИНИЦЕ

ВЫБОРКИ

ПРЕДЕЛ

ОШИБКИ

(колонки

2x3x4),

ДОЛ.

Завышения

0,030

0,017

0,015

0,014

0,013

1200000

1,0

0,671

0,07

0,016

0,0002

36000

13688

1260

269

Верхний

предел

0,089

51220

Верхняя

предельная

ошибка

51220

Занижения

0,030

0,017

1200000

1,0

0,03

36000

612

Нижний

предел

0,047

Нижняя

предельная

ошибка

36612

• Риск ошибочного принятия равен 5%; объем

выборки - 100.

РЕШИТЕ ВОПРОС О ПРИЕМЛЕМОСТИ СОВОКУПНОСТИ. Всякий

раз, когда используется статистический метод, требуется правило для

принятия решения о приемлемости ювокуп нести. Для монетарной вы-

борки это правило таково:

Если нижний предел ошибки (lower error bound - LEB) и

верхний предел ошибки (upper error bound - UEB) находят- ся

между величинами допустимой ошибки завышения и

допустимой ошибки занижения, делается вывод о том, что

балансовая стоимость не содержит существенных ошибок. В

противном случае делается вывод о наличии существенных

ошибок.

448 ВЫБОЮЧНОЕ ИССЛЕДОВАНИЕДЛЯПРОВЕРОКСТАТЕЙБАЛАНСА

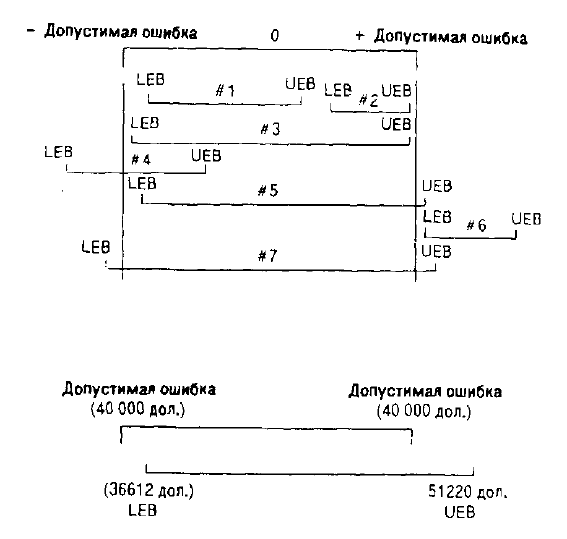
Это правило проиллюстрировано на следующей схеме: аудитор должен

придти к выводу, что LEB и UEB для случаев 1, 2, 3 целиком находятся

в пределах допустимых ошибок завышения и занижения. Следовательно,

принимается решение об отсутствии существенных ошибок в совокупно-

сти по величине допустимой ошибки. В случаях 4, 5, 6, 7 или LEB либо

UEB, или оба предела выходят за рамки допустимой ошибки. Следова-

тельно, балансовая оценка совокупности отвергается.

Предположим, в нашем примере аудитор установил допустимую ошиб-

ку завышения или занижения равной 40 ООО дол. Это означает, что он

примет отраженную в учете величину, если убедится в завышении или

занижении общей суммы дебиторской задолженности не более чем

на 40 ООО дол. Как было показано ранее, аудитор получил выборку из

ста единиц, нашел 5 ошибок и рассчитал, что нижний предел должен

быть 36 612 дол., а верхний - 51 220 дол. Применение правила принятия

решения приводит аудитора к выводу о том , что етвокупность не может

быть принята, поскольку верхний предел ошибки больше допустимой

ошибки 40 ООО дол.