Balakumar Balachandran, Magrab E.B. Vibrations
Подождите немного. Документ загружается.


The significance of these results is illustrated with several examples, where
free oscillations of underdamped systems due to impacts are considered.
EXAMPLE 4.4
Impact of a vehicle bumper
2
Consider a vehicle of mass m that is travelling at a constant velocity V
o
as
shown in Figure 4.6a. The bumper is modeled as a spring k and viscous damper
c in parallel. If the vehicle’s bumper hits a stationary barrier, then after the im-
pact, the displacement and velocity of the mass are those given by Eqs. (4.13)
and (4.14), respectively. These results are used to determine the coefficient of
restitution of the system and the amount of energy that has been dissipated un-
til the time the bumper is no longer in contact with the barrier.
The bumper is in contact with the barrier only while the sum of the forces
that is, while the spring-damper combination is being compressed. At the in-
stant when they are no longer in compression the acceleration is zero; that is,
the time at which the sum of these forces on the mass is zero. The first time
instance at which the acceleration is zero is given by Eq. (4.20) for p 0, and
the corresponding velocity is given by Eq. (4.21).
Based on Newton’s law of impact, the coefficient of restitution P is de-
fined as
(a)
where v
vehicle
is the vehicle velocity, v
barrier
is the velocity of the barrier, and the
assumption that v
barrier
is zero has been used; that is, the barrier is fixed. Then,
making use of Eq. (a) and Eq. (4.21) with p 0, we find that
(b)
We now make use of Eq. (b) to examine how the coefficient of restitution
P depends on the damping factor z. Considering first the undamped case, we
note from Eq. (4.15) that w/tan w→0as , and, therefore, . In other
words, there are no losses and the system leaves with the same velocity with
which it arrived. This is consistent with the fact that this is an elastic collision.
When , the system becomes critically damped and w/tan w →1 and,
therefore, from Eq. (b), we find that ; that is, the mass leaves the bar-
rier with a velocity of 0.135V
o
.
P 씮 e
2
z 씮 1
P 씮 1z 씮 0
P
x
#
1t
vm
2
x
#
10 2
V
o
e
2w/tan w
V
o
e
2w/tan w
P
1v
vehicle
v
barrier
2
after impact
1v
vehicle
v
barrier
2
before impact
1v
vehicle
2
after impact
1v
vehicle
2
before impact
kx1t 2 cx
#
1t 2 0
140 CHAPTER 4 Single Degree-of-Freedom System
2
See also, V. I. Babitsky, Theory of Vibro-Impact Systems and Applications, Springer-Verlag,
Berlin, Appendix I (1998).
The amount of energy that the system dissipates during the interval 0
t t
vm
is the difference between the initial kinetic energy and the kinetic
energy at separation. Note that the vehicle does not have any potential energy
when it is not in contact with the barrier. Thus,
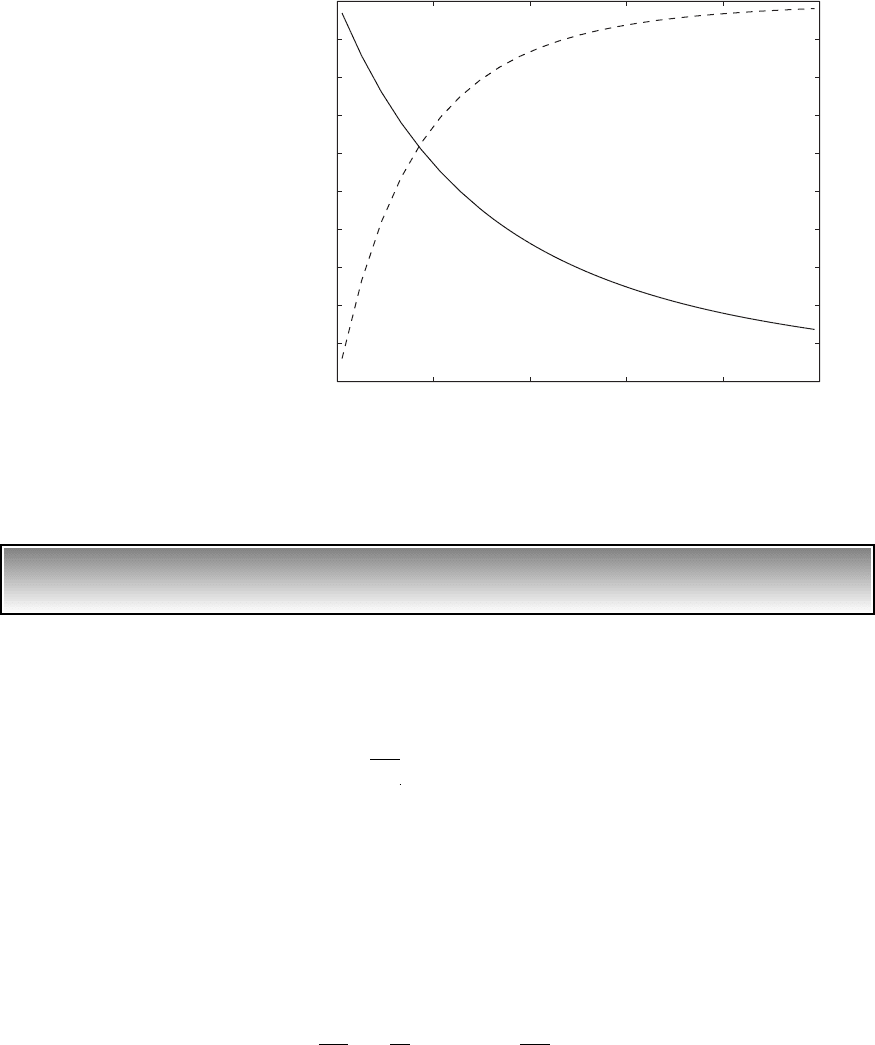
or
where E
init
is given by Eq. (4.27). These results are summarized in Figure 4.7.
It is noted that these results have been obtained for a collision with a single
impact.
E
diss
E
init
31 e
4w/tan w
4
E
diss
1
2
mV
o
2
1
2
m3x
#
1t
vm
24
2
1
2
mV
o
2
1
2
mV
o
2
e
4w/tan w
4.2 Free Responses of Undamped and Damped Systems 141
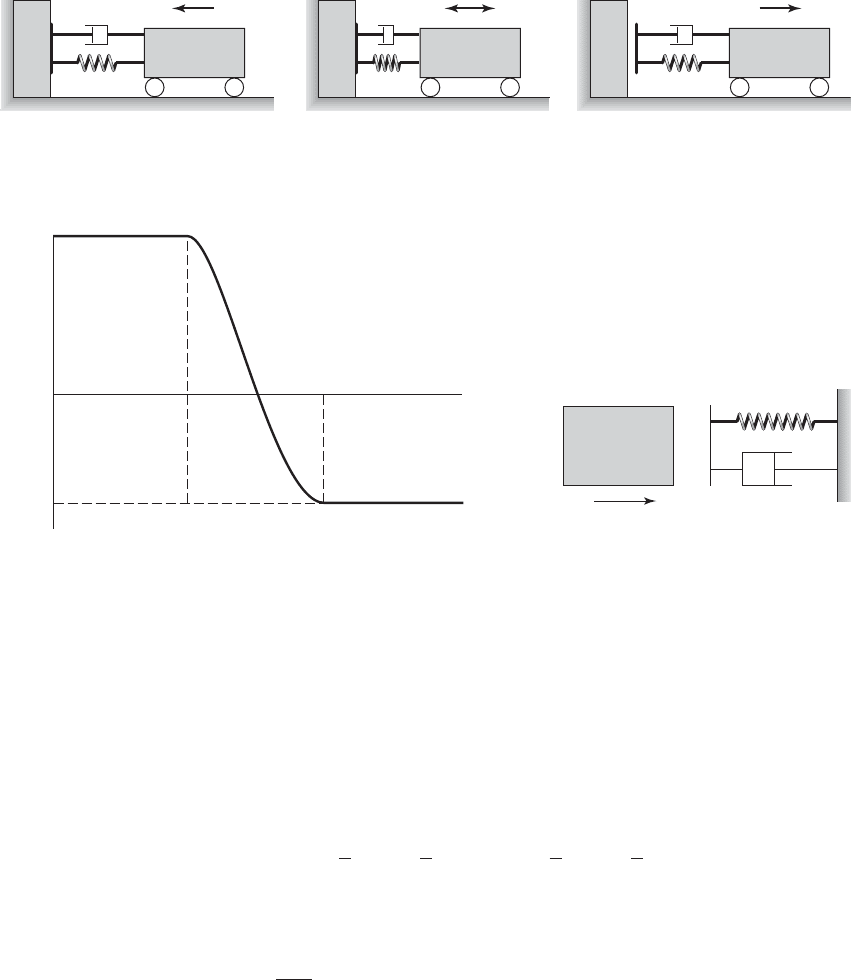
FIGURE 4.6
(a) Model of a car bumper colliding with a stationary barrier, (b) time history of velocity of mass, and (c) equivalent impact configu-
ration. In this equivalent configuration, a mass moving with a velocity V
o
impacts a barrier, which is represented by a spring and
damper combination.
k
c
m
V
o
Barrier
Bumper makes contact
with barrier at t t
o
k
c
m
v(t)
Bumper in contact with
barrier for t
o
t t
vm
t
o
Bumper no longer in contact
with barrier for t t
vm
t
o
k
c
m
v(t
vm
)
(a)
V
o
v(t)
t
o
t
vm
t
o
t
v(t
vm
)
(b)
Rigid system
0
Rigid systemOscillator
(c)
k
c
m
V
o
EXAMPLE 4.5 Impact of a container housing a single degree-of-freedom system
We shall now consider the effects of dropping onto the floor a system that re-
sides inside a container that has a coefficient of restitution P with respect to
the floor. The system is shown in Figure 4.8. If the container falls from a
height h, then the magnitude of the velocity at the time of impact with the
floor is
At the instant t 0
after impact, the container bounces upwards with a ve-
locity whose magnitude is PV
o
. Then at t 0
, the container and the single
degree-of freedom system can be modeled as a single degree-of freedom sys-
tem with a moving base as discussed in Section 3.5. Thus, if we define the rel-
ative displacement
(a)
then, from Eq. (3.30) we have
(b)
However, , since the container is decelerating during the rebound
upwards. Then Eq. (b) becomes
y
$
g
m
d
2
z
dt
2
c
dz
dt
kz m
d
2
y
dt
2
z1t 2 x1t 2 y1t2
V
o
22gh
142 CHAPTER 4 Single Degree-of-Freedom System
FIGURE 4.7
Coefficient of restitution and fraction of energy dissipation for impacting single degree-of-
freedom system.
0 0.2 0.4 0.6 0.8 1
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
e
E
diss
/E
init
z
e, E
diss
/E
init

4.2 Free Responses of Undamped and Damped Systems 143
(c)
where u(t) is the unit step function. The initial conditions are
(d)
The solution to Eq. (c) for 0 z 1 and subject to the initial conditions
given by Eq. (d) is determined from Eq. (D.11). Thus, after substituting
f(t) mgu(t), we find that
(e)
where w is given by Eq. (4.15), d
st
mg/k, and the coefficient of restitution-
dependent parameter R is
(f)
The corresponding velocity is
(g)
1
21 z
2
e
zv
n
t
sin121 z
2
v
n
t2
z
#
1t 2
d
st
v
n
R
21 z
2
e
zv
n
t
sin121 z
2
v
n
t w2
R 11 P2
A
2h
d
st
1
1
21 z
2
e
zv
n
t
sin121 z
2
v
n
t w2
z1t 2
d
st
R
21 z
2
e
zv
n
t
sin121 z
2
v
n
t2
11 P2V
o
11 P212gh
z
#
10 2 x
#
10 2 y
#
10 2V
o
1PV
o
2
z10 2 x10 2 y102 0
m
d
2
z
dt
2
c
dz
dt
kz mgu1t2
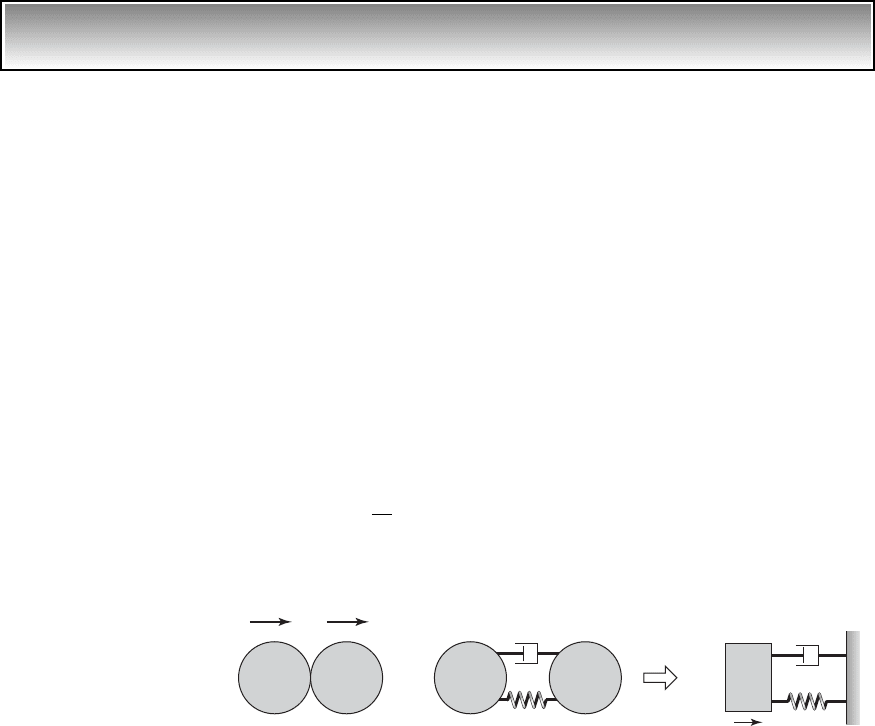
FIGURE 4.8
Single degree-of-freedom system inside a container: (a) dropped from a height h and
(b) on rebound immediately after impact with the floor.
V
o
V
o
g
k
c
m
k
h
c
x
m
(a) (b)
y

144 CHAPTER 4 Single Degree-of-Freedom System
The extremum of the relative displacement is determined from z
max
z(t
max
)
where t
max
is the earliest time at which . In this particular case, an
explicit analytical expression for t
max
cannot be found, so the maximum dis-
placement is determined numerically from Eq. (e). The magnitude of the
maximum displacement is a function of the initial velocity, which is a func-
tion of the drop height h, the coefficient of restitution of the container, and the
damping ratio and the static displacement of the spring of the single degree-
of-freedom system inside the container. The numerically obtained results are
shown in Figure 4.9. We see that there are many ways by which one can de-
crease the maximum relative displacement of the mass, which lead to the fol-
lowing design guidelines.
z
#
1t
max
2 0
Design Guidelines: To minimize the maximum relative displace-
ment of the mass, keep h and, therefore the velocity V
o
, as small as pos-
sible. Make the container of a material that absorbs the impact, so that
the coefficient of restitution is as small as possible. Make the natural
frequency of the single degree-of-freedom system as low as possible.
Since, in packaging, the mass is usually not a parameter that can be
specified, one has to make the equivalent spring as soft as practical. In-
crease the equivalent damping of the packing material.
FIGURE 4.9
Normalized maximum relative displacement of a system inside a container that is dropped
from a height h as a function of coefficient of restitution of the container and the damping
ratio of the single degree-of-freedom system.
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7
0
1
2
3
4
5
6
7
8
9
10
R
1
R
3
R
6
R
10
z
|z
max
/
d
st
|
Although not explored here, an equally important design goal is to min-
imize the absolute acceleration of the mass m, as large accelerations can be
detrimental to the single degree-of-freedom system.
EXAMPLE 4.6
Collision of two viscoelastic bodies
We use the single degree-of-freedom model to analyze the impact
3
(collision)
of two viscoelastic bodies. In Figure 4.10, two bodies m
A
and m
B
whose rela-
tive velocity is V
AB
just before impact is shown. During contact, the contact
force between the masses m
A
and m
B
is represented by using a Kelvin-Voigt
model: that is, a linear spring with stiffness k in parallel with a viscous damper
with damping coefficient c.
If we let x
A
and x
B
represent the absolute displacements of m
A
and m
B
, re-
spectively, then the relative displacement between the two masses, the rela-
tive velocity between them, and the relative acceleration between them are
given by, respectively,
(a)
The magnitude of the contact force F
AB
that acts on each mass for the dura-
tion of contact is
(b)F
AB
c
dz
dt
kz
z
$
x
$
A
x
$
B
V
AB
z
#
x
#
A
x
#
B
z x
A
x
B
4.2 Free Responses of Undamped and Damped Systems 145
3
C. Rajalingham and S. Rakheja, “Analysis of Impact Force Variation During Collision of Two
Bodies Using a Single-Degree-of-Freedom System Model,” J. Sound Vibration, Vol. 229, No. 4,
pp. 823–835 (2000). For the case where both masses are traveling in the same direction in
contact with each other and impact a rigid wall, see W. J. Stronge, Impact Dynamics, Cambridge
University Press, Cambridge, U.K., Chapter 5 (2000). For the collision of two single degree-of-
freedom oscillators, see R. J. Pinnington, “Collision of Two Adjacent Oscillators,” J. Sound Vi-
bration, 268, pp. 343–360, 2003.
FIGURE 4.10
Impact of two viscoelastic bodies.
k
c
k
z
c
m
m
A
m
A
m
B
m
B
V
B
V
A
z(0) 0
z(0) V
AB
.
Viscoelastic bodies
just prior to impact
Viscoelastic bodies
during impact
Model of viscoelastic
bodies during impact
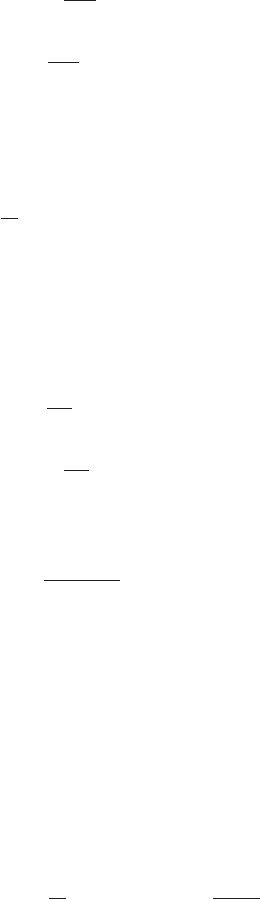
From the free-body diagram of each mass during impact, we arrive at
(c)
Since there are no external forces acting on the system at the time of impact,
the system’s linear momentum is conserved. Thus, from Eqs. (1.11) and
(1.12), we have that
(d)
and, therefore,
(e)
From Eq. (e) and the last of Eqs. (a), we find that
(f)
where the quantity m is called the effective mass and it is given by
(g)
Then, from Eqs. (a), (b), (c), (f), and (g), we find that when the masses
are in contact, the governing equation for the effective mass of the colliding
bodies is given by
or
(h)
where
and (i)
Equation (h) is valid up until the time that F
AB
0, which, from the above
equation, is also the time at which . Noting that the initial conditions are
z(0) 0 and , the solution for the relative displacement z between
the two masses is given by Eq. (4.13) where V
o
V
AB
. The coefficient of resti-
tution can be determined from Eq. (a) of Example 4.4.
z
#
10 2 V
AB
z
$
0
z
c
2mv
n
v
n
2
k
m
z
$
2zv
n
z
#
v
n
2
z 0
mz
$
F
AB
1cz
#
kz2
m
m
A
m
B
m
A
m
B
x
$
B
m
m
B
z
$
x
$
A
m
m
A
z
$
m
A
x
$
A
m
B
x
$
B
0
d
dt
1m
A
x
#
A
m
B
x
#
B
2 0
x
$
B
F
AB
m
B
x
$
A
F
AB
m
A
146 CHAPTER 4 Single Degree-of-Freedom System
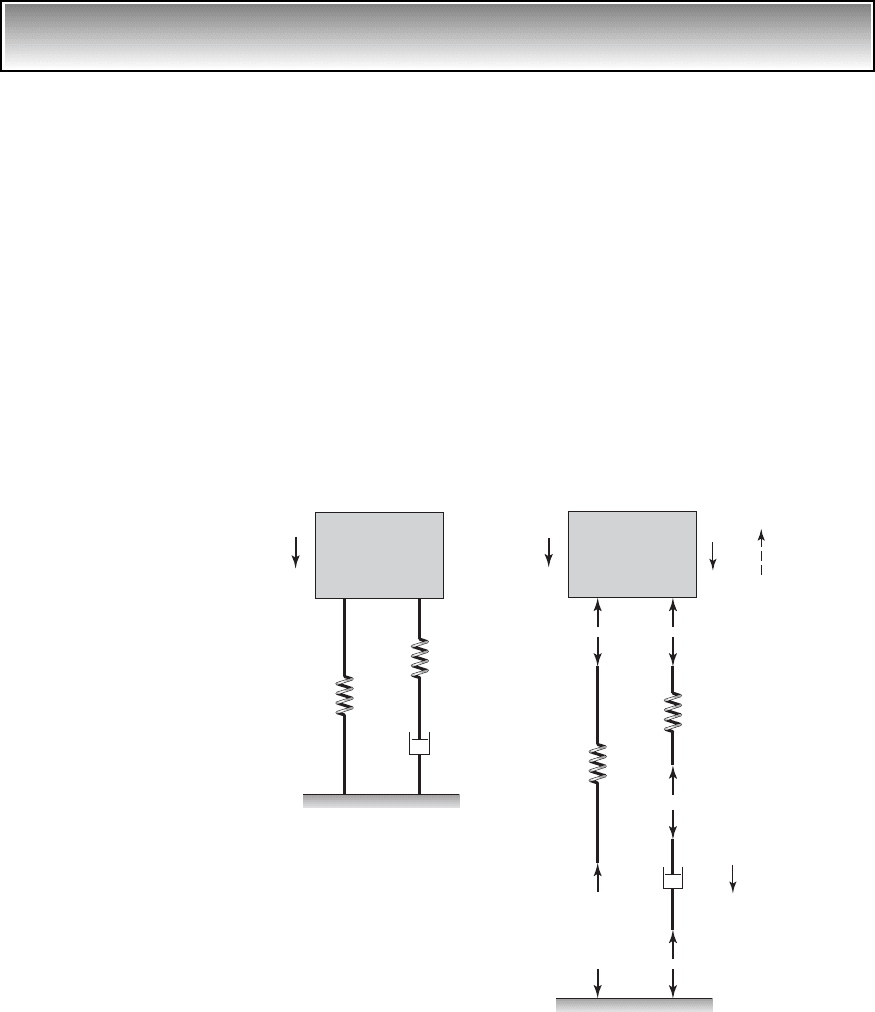
EXAMPLE 4.7 Vibratory system employing a Maxwell model
We shall now modify the single degree-of-freedom system shown in Figure
3.1 to obtain a more realistic description of the reaction force transmitted to
the fixed support, when the inertial element is given an initial velocity. As
noted earlier, if a Kelvin-Voigt model is used, there is an instantaneous reac-
tion force at the base when an initial velocity is imparted to the mass. This un-
realistic response is eliminated by using the modified system shown in Fig-
ure 4.11a, where we have introduced a linear spring k
1
in series with a linear
viscous damper c. The combination of the linear spring k
1
in series with the
linear viscous damper c is called a Maxwell model. To describe the motion of
the system, we need, in addition to the displacement variable x of the mass m,
another displacement variable x
d
to describe the displacement at the spring-
damper junction in the Maxwell model. Both x and x
d
are measured from their
respective static-equilibrium positions.
Governing Equations of Motion and Solution for Response
The governing equations are obtained for the general case with forcing and,
from this case, the free response of the mass subjected to an initial velocity is
4.2 Free Responses of Undamped and Damped Systems 147
FIGURE 4.11
(a) Single degree-of-freedom system with a spring added in series with the damper and
(b) forces on the system’s elements.
k
c
m
k
1
f
(t)
k
c
x
m
k
1
f(t)
mx
..
.
F
1
k
1
(x x
d
)
F
1
cx
d
.
F
1
cx
d
F kx
F
kx
x
d
(a) (b)

determined. Making use of Figure 4.11b and carrying out a force balance
along the vertical direction for the mass m and a force balance for the
Maxwell element, we arrive at
(a)
Since we have an additional first-order equation, apart from the second-order
equation typical of a single degree-of-freedom system, the vibratory system of
Figure 4.11 is also referred to as a one and a half degree-of-freedom system.
Introducing the natural frequency
(b)
and the nondimensional quantities
(c)
Eqs. (a) are rewritten as
(d)
and the overdot indicates the derivative with respect to t and
(e)
In the limiting case, when (i.e., ), the second of Eqs. (d) leads
to a Kelvin-Voigt model with a linear spring of stiffness k in parallel with a
linear damper with damping coefficient c. Therefore, Eqs. (d) can be used to
study a vibratory system with a Maxwell model as well as a Kevin-Voigt
model.
If we represent the Laplace transform of x(t) by X(s), the Laplace trans-
form of x
d
(t) by X
d
(s), and the Laplace transform of f(t) by F(s), then, from
pair 2 in Table A of Appendix A, the Laplace transforms of Eqs. (d) are
(f)
where we have assumed that x
d
(0) 0, and used the notation
(g)
Upon solving for X(s) and X
d
(s) from Eqs. (f), we obtain, respectively,
G1s 2
F1s 2
k
sx10 2 x
#
10 2
gX1s 2 1g 2zs 2X
d
1s 2 0
1s
2
1 g2X1s2 gX
d
1s 2 G1s2
k
1
씮 qg 씮 q
2z
cv
n
k
gx gx
d
2zx
#
d
x
$
11 g 2x gx
d
f 1t 2/k
g
k
1
k
t v
n
t
v
n
A
k
m
k
1
1x x
d
2 c
dx
d
dt
m
d
2
x
dt
2
kx k
1
1x x
d
2 f 1t 2
148 CHAPTER 4 Single Degree-of-Freedom System

(h)
Force Transmitted to the Fixed Support
From Figure 4.11b, the reaction force on the base is seen to be
(i)
which, in terms of the nondimensional quantities given by Eqs. (c), is writ-
ten as
(j)
where the overdot is the derivative with respect to t. Upon taking the Laplace
transform of Eq. (j), again assuming that x
d
(0) 0, and using Eqs. (h), we
find that
(k)
This expression will be revisited in Example 5.13.
We shall limit the rest of our discussion to the case where the applied
force and the initial displacement are zero; that is, f(t) 0 and x(0) 0, and
the initial velocity is
(l)
Therefore, Eq. (g) simplifies to
(m)
Upon substituting Eq. (m) into Eq. (k), we arrive at
(n)
Before evaluating Eq. (n), we recall that the limiting case when (i.e.,
) recovers the Kelvin-Voigt model, where a linear spring k is in paral-
lel with a linear viscous damper c. For this limiting case, we divide the nu-
merator and denominator of Eq. (n) by g and take the limit as . This
operation results in
(o)
F
B
1kV
o
/v
n
2
1 2zs
s
2
2zs 1
g 씮 q
k
1
씮 q
g 씮 q
F
B
1kV
o
/v
n
2
g 2z11 g2s
2zs
3
gs
2
2z11 g2s g
G1s 2
V
o
v
n
dx10 2
dt
v
n
dx10 2
dt
V
o
F
B
k
G1s 23g 2z11 g 2s 4
2zs
3
gs
2
2z11 g2s g
F
B
k
2zx
#
d
x
F
B
F
1
F c
dx
d
dt
kx
X
d
1s 2
gG1s 2
2zs
3
gs
2
2z11 g2s g
X1s 2
G1s 21g 2zs2
2zs
3
gs
2
2z11 g2s g
4.2 Free Responses of Undamped and Damped Systems 149
