Balakumar Balachandran, Magrab E.B. Vibrations
Подождите немного. Документ загружается.


160 CHAPTER 4 Single Degree-of-Freedom System
The value of t
max
is obtained from Eqs. (4.37), (4.38), (c) and Figure 4.19
in the following manner. We note that
(d)
From Figure 4.19, it is seen that the maximum displacement is 1.8X
o
, which
occurs when v(t) 0. Then, Eq. (4.37) becomes
(e)
which we solve numerically
8
to obtain t
max
0.945.
0.91 e
0.1t
max
sin10.995t
max
0.532
1.8X
o
1.976X
o
e
0.1t
max
sin1t
max
21 10.1 2
2
0.532
w
d
tan
1
21 10.1 2
2
1.6 0.1
tan
1
0.5853 0.53 rad
A
o
X
o
B
1
11.6 0.12
2
1 10.1 2
2
1.976X
o
V
r
v10 2
x10 2v
n
1.6X
o
v
n
X
o
v
n
1.6
FIGURE 4.19
State-space graph for a system with prescribed initial velocity and prescribed
initial displacement.
1.2
.8
.4 0 .4 .8 1.2 1.6
1.5
1
0.5
0
0.5
1
1.5
x(t)/X
o
v(t)/(X
o
v
n
)
(x(0),v(0))
(0.95,0)(0.5,0)
8
The MATLAB function fzero was used.

The time
max
can also be obtained from Eq. (4.39), which is the earliest
time that v(
max
) 0; that is, the time at which the argument of the sine func-
tion is zero. Thus, we have
(f)
or equivalently
(g)
Since
(h)
we find that
(i)
4.3 STABILITY OF A SINGLE DEGREE-OF-FREEDOM SYSTEM
A linear single degree-of-freedom system is considered stable if, for all se-
lections of finite initial conditions and finite forcing functions,
where A has a finite value. This is a boundedness condition, which requires
the system response x(t) be bounded for bounded system inputs. If this is not
the case, then the system is considered unstable.
9
For the systems that are
dealt with in this book, the unstable responses grow either linearly with time
or exponentially with time.
Instability of Unforced System
We consider an unforced vibratory system subjected to finite initial condi-
tions and study when this system can be unstable. To this end, we start from
the solution for the response given in the Laplace domain by Eq. (D.2) and set
F(s) 0 to obtain
(4.40)X1s 2
sx10 2
D1s 2
2zv
n
x10 2 x
#
10 2
D1s 2
0x1t 20 A
t 0
t
max
1.47 0.53
0.995
0.945
w tan
1
21 z
2
z
tan
1
0.995
0.1
1.47 rad
t
max
w w
d
21 z
2
v
d
t
max
w
d
w t
max
21 z
2
w
d
w 0
4.3 Stability of a Single Degree-of-Freedom System 161
9
Other notions of stability can be found in A. H. Nayfeh and B. Balachandran, Applied Nonlin-
ear Dynamics: Analytical, Computational and Experimental Methods, John Wiley & Sons, NY
(1995).

Now let us examine the denominator D(s), which is given by Eq. (D.3);
that is,
(4.41)
where we have used , and
(4.42)
and we have switched to the more general equivalent forms for the inertia,
stiffness, and damping. From Eq. (4.40), we see that there are two terms on
the right-hand side that involve, respectively, the polynomial ratios
(4.43)
and
(4.44)
Since
where L
1
indicates the inverse Laplace transform, it is seen that in order to
obtain x(t) one needs the inverse Laplace transforms of Eqs. (4.43) and (4.44),
which are
where we have used Laplace transform pair 7 in Table A of Appendix A.
The condition under which
remains finite for t 0 is
(4.45)
that is, the real parts of the roots have to be less than or equal to zero. From
Eq. (4.42), it is seen that this condition is satisfied when c
e
0 and k
e
0.
When either c
e
0 or k
e
0, the system is unstable. These results are usu-
ally summarized in a root locus diagram like that shown in Figure 4.20 in
which the roots s
1
and s
2
are plotted in the complex plane for different values
of the damping parameter z.
Re3s
1,2
4 0
e
s
1,2
t
L
1
c
1
s s
1,2
d e
s
1,2
t
x1t 2 L
1
3X1s24
s
D1s 2
s
1s s
1
21s s
2
2
1
1s
2
s
1
2
c
s
2
1s s
2
2
s
1
1s s
1
2
d
1
D1s 2
1
1s s
1
21s s
2
2
1
1s
1
s
2
2
c
1
1s s
1
2
1
1s s
2
2
d
s
1,2
1
2m
e
3c
e
2c
e
2
4m
e
k
e
4
z c
e
/12m
e
v
n
2, v
n
2k
e
/m
e
1s s
1
21s s
2
2
D1s 2 s
2
2zv
n
s v
n
2
s
2
1c
e
/m
e
2s k
e
/m
e
162 CHAPTER 4 Single Degree-of-Freedom System

EXAMPLE 4.11 Instability of inverted pendulum
The inverted pendulum that was examined in Example 3.11 is a system that
can be unstable, depending on the values of the parameters. For this system,
we have m
e
0, c
e
0, and
Thus, the system is stable as long as k
e
0; that is, when
Asymptotic Stability
So far, we have only discussed the notion of bounded stability and how
the system parameters such as equivalent stiffness k
e
and equivalent damping
coefficient c
e
can affect the stability of the system. A notion of stability that
kL
1
2
m
1
gL
1
m
2
g
L
2
2
k
e
kL
1
2
m
1
gL
1
m
2
g
L
2
2
4.3 Stability of a Single Degree-of-Freedom System 163
FIGURE 4.20
Root locus diagram.
Imag(s)
Stable region
(Always stable
when k
e
0
and c
e
0)
s
2
( 0)
s
2
(0 1)
s
1
(0 1)
s
1
( 1)
(→ as ↑)
s
1
( 0)
s
1,2
()
n
[ (
2
1)
1/2
]
s
2
( 1) s
1
( 1)
s
2
( 1)
(← as ↑)
Real(s)
Unstable region
(Unstable when k
e
0
and/or c
e
0)

is useful for studying the oscillations of vibratory systems is asymptotic
stability.
10
Instead of defining this motion for a general system, let us consider
Eq. (4.2). Then
(4.46)
The equilibrium position x 0 of this system is said to be asymptotically sta-
ble if
(4.47)
that is, the equilibrium position is approached as time increases. Since the
governing equation is an equation with constant coefficients, a solution to this
equation can be written in the form
(4.48)
where A is a constant and l is an unknown quantity. Upon substituting Eq.
(4.48) into Eq. (4.46) and requiring that A 0, we obtain
(4.49)
Equation (4.49) is referred to as the characteristic equation and the roots of
this equation l
1
and l
2
are referred to as characteristic roots or eigenvalues.
The eigenvalues are special values for which x(t) given by Eq. (4.48) has a
non-zero value. The roots of Eq. (4.49) are given by
(4.50)
Therefore, the solution given by Eq. (4.48) is written as
(4.51)
Hence, if the real parts of the exponents l
1
and l
2
are negative, Eq. (4.47) is
satisfied, and the equilibrium position is asymptotically stable. It should not
be surprising that the polynomial in Eq. (4.49) is identical to Eq. (4.41) and
that the requirement that the real parts of the exponents be negative for sta-
bility is identical to Eq. (4.45), because they both pertain to the free oscilla-
tions of the system described by Eq. (4.46).
It is clear that when the damping factor is positive—that is, z 0—the
real parts of the exponents l
i
are negative and hence, this ensures stability, in
particular, asymptotic stability. On the other hand, for negative damping fac-
tors that are possible in the presence of fluid forces in certain physical sys-
tems, the exponents have positive real parts indicating instability.
x1t 2 A
1
e
l
1
t
A
2
e
l
2
t
l
1,2
v
n
3z 2z
2
14
l
2
2zv
n
l v
n
2
0
x1t 2 Ae
lt
lim
t씮 q
x1t 2씮 0
d
2
x
dt
2
2zv
n
dx
dt
v
n
2
x 0
164 CHAPTER 4 Single Degree-of-Freedom System
10
A. H. Nayfeh and B. Balachandran, ibid.

4.4 MACHINE TOOL CHATTER
In Figure 4.21, a model of a turning operation on a lathe is shown. When the
cutting parameters such as spindle speed and width of cut are carefully cho-
sen, the turning operation can produce the desired surface finish on the work
piece. However, this turning operation can become unstable for certain values
of spindle speed and width of cut. When these undesirable conditions are
present, the tool and work piece system “chatters,” producing an undesirable
surface finish and a shortening of tool life. In this section, we shall explore the
loss of stability that leads to the onset of chatter.
For a rigid work piece and a flexible tool, the cutting force acting on the
tool due to the uncut material and the associated damping can be modeled as
shown in Figure 4.21. The mass m represents the mass of the tool and tool
holder, k is the stiffness of the tool holder’s support structure, and c is the
equivalent viscous damping of the structure. The dynamic cutting force F
c
is
the sum of the forces due to the change in chip thickness and the change in
the penetration rate of the tool.
11
Thus, we have
where m is the overlap factor (0 m 1), k
1
is an experimentally determined
dynamic coefficient called the cutting stiffness, K is the experimentally deter-
mined penetration rate coefficient, and N is the rotational speed of either the
tool or the work piece in revolutions per second. Then carrying out a force
balance based on Figure 4.21, the tool vibrations can be described by the fol-
lowing equation
(4.52a)
Time-delay effect due to uncut
chip during previous pass
d
2
x
dt
2
a
1
Q
K
k
b
dx
dt
a1
k
1
k
bx m
k
1
k
x1t 1/2 0
DampingChange in chip thicknessCutting
stiffness
F
c
k
1
3x1t2 mx1t 2p/N 24 K
2p
N
dx
dt
4.4 Machine Tool Chatter 165
FIGURE 4.21
Model of a tool and work piece during turning.
k
c
k
1
x
x
K
N
m
Work
piece
Tool
Work piece Tool
F
c
⎫
⎬
⎭
⎫
⎪
⎪
⎪
⎬
⎪
⎪
⎪
⎭
⎫
⎬
⎭
⎫
⎪
⎪
⎬
⎪
⎪
⎭
11
S. A. Tobias, Machine-Tool Vibration, Blackie & Sons, Ltd., Glasgow, pp. 146–176 (1965).

where the nondimensional time t v
n
t, and
(4.52b)
In Eqs. (4.52b), the quantity Q is called the quality factor, which is discussed
in Section 5.3.3.
Since the right-hand side of Eq. (4.52a) is zero, the governing equation is
similar to that used to study the free response of a single degree-of-freedom
system. However, unlike the other systems treated so far, the system described
by Eq. (4.52a) has a time delay 1/ present. This makes the system, which is
a linear, delay-differential equation, more difficult to deal with when com-
pared to the ordinary differential equations we have considered so far. For this
system, when the position x(t) 0 is stable, the cutting operation is stable.
Physically, the position x(t) 0 corresponds to cutting at the specified nom-
inal chip thickness. When this position is unstable, the system can start to
chatter. The onset of chatter is marked by tool oscillations. To determine the
onset of these oscillations, the conditions that can lead to oscillatory solutions
of Eq. (4.52a) are examined next.
A solution to Eq. (4.52a) is of the form
which, when substituted into Eq. (4.52a) gives the characteristic equation
(4.53)
where, in general, the exponent is complex and of the form l d jv. For
the system to be stable, the Re[l] 0, that is, d 0. The boundary between
the stable and unstable regions corresponds to d 0. When the exponent
is purely imaginary, the response of the tool is oscillatory. Therefore, to find
the stability boundary we let l jv and substitute this value into the quasi-
polynomial Eq. (4.53). After setting the real and imaginary parts to zero, we
obtain two equations from which the chatter frequency v and parameter of in-
terest are determined as a function of the nondimensional spindle speed .
Here, we seek to determine the quality factor Q as a function of , which is
indicative of the damping level in the system.
On substituting l jv into Eq. (4.53), and separating the real and imag-
inary parts, we arrive at
(4.54)v
2
1
k
1
k
11 m cos1v/22
1
Q
K
k
mk
1
k
sin1v/2
v
0
l
2
a
1
Q
K
k
bl 1
k
1
k
11 me
l/
2 0
x Ae
lt
N
2pv
n
,
v
n
A
k
m
,
Q
1
2z
,
and
2z
c
mv
n
166 CHAPTER 4 Single Degree-of-Freedom System
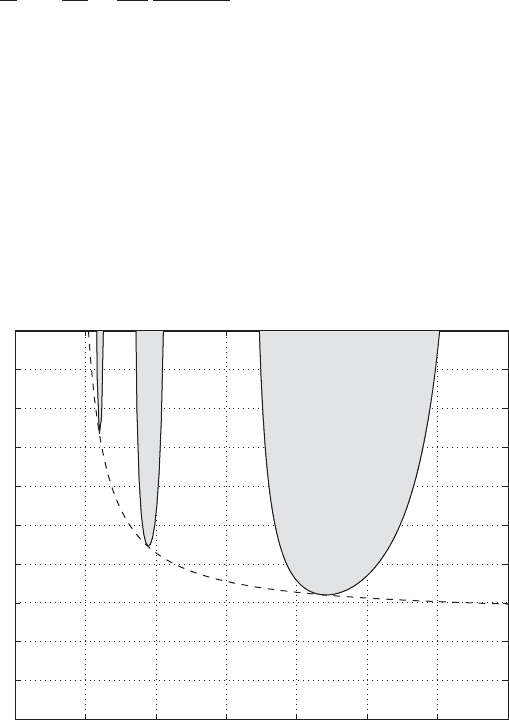
In Eqs. (4.54), the quantities K/k, m, and k
1
/k are known, and the values
of the nondimensional spindle speed are varied over a specified range. At
each value of , the value of v is determined numerically
12
from the second
of Eqs. (4.54). The values for and v are then used in the first of Eqs. (4.54)
to determine the positive values of Q that satisfy the equation; that is, those
values of and v for which
In the plot of versus Q, we can show the regions for which the system is ei-
ther stable or unstable. Representative results are shown in Figure 4.22. The
shaded regions, which are in the form of lobes, are regions of instability, and
are referred to as stability lobes. The asymptote to these lobes is shown
in the figure by a dashed line. If one conservatively chooses the cutting pa-
rameters so that one is below this asymptote to the lobes, then based on the
linear theory presented here, the tool will not chatter. Of course, one can also
choose spindle speeds that correspond to regions between the stability lobes
as well.
1
Q
K
k
mk
1
k
sin1v/2
v
4.4 Machine Tool Chatter 167
12
The MATLAB function fzero was used.
FIGURE 4.22
Stability chart for one set of parameters in turning: m 1.
0 0.05 0.1 0.15 0.2 0.25 0.3 0.35
0
5
10
15
20
25
30
35
40
45
50
Ω
Q
Unstable
Stable
K/k
0.0029
k
1
/k
0.0785

4.5 SINGLE DEGREE-OF-FREEDOM SYSTEMS WITH NONLINEAR ELEMENTS
4.5.1 Nonlinear Stiffness
We illustrate the effects that two different types of nonlinear springs can have
on the free response of a system when subjected to either an initial displace-
ment or initial velocity.
System with Hardening Cubic Spring
First, we consider a system that has a spring whose stiffness includes a com-
ponent that varies as the cube of the displacement. After using Eq. (2.23) for
the nonlinear spring force, the governing equation is
(4.55)
where the nondimensional time variable t v
n
t. We solve Eq. (4.55) numer-
ically,
13
since it does not have an analytical solution. We assume that
a 1 cm
2
, z 0.15, and that the initial conditions are X
o
2 cm and
V
o
0. The results are shown in Figures 4.23, along with the solution for the
system with a linear spring; that is, when a 0.
We see from these results that the response of the system with the non-
linear spring is distinctly different from that with the linear spring. First, the
response of the system with the nonlinear spring does not decay exponentially
with time and second, the displacement response does not have a constant
period of damped oscillation. These differences provide one a means of dis-
tinguishing one type of nonlinear system from a linear system based on an
examination of the response to an initial displacement. In practice, the
nonuniformity of the period is easier to detect, since the dependence of fre-
quency (or period) on the amplitude of free oscillation is a characteristic of
a nonlinear system.
System with Piecewise Linear Springs
We now consider a second nonlinear system shown in Figure 4.24. In this case,
the springs are linear; however, the mass is straddled by two additional linear
elastic spring-stops that are not contacted until the mass has been displaced by
an amount d in either direction. The stiffness of the springs is proportional to
the attached spring by a constant of proportionality m (m 0). When m 0, we
have the standard linear single degree-of-freedom system, and when m 1, the
elastic spring-stops are stiffer than the spring that is permanently attached to
the mass. The governing equation describing the motion of the system is
14
d
2
y
dt
2
2z
dy
dt
y mh1y2 0
d
2
x
dt
2
2z
dx
dt
x ax
3
0
168 CHAPTER 4 Single Degree-of-Freedom System
13
The MATLAB function ode45 was used.
14
H. Y. Hu, “Primary Resonance of a Harmonically Forced Oscillator with a Pair of Symmetric
Set-up Elastic Stops,” J. Sound Vibration, Vol. 207, No. 3, pp. 393–401, 1997.

FIGURE 4.23
Comparison of the responses of linear (solid lines) and nonlinear (dashed lines) systems with
prescribed initial displacement: (a) displacement and (b) phase portrait.
0 5 10 15
2
1.5
1
0.5
0
0.5
1
1.5
2
t
x(t)
t
A
t
B
t
A
3.31
t
B
t
C
t
B
4.99
t
C
(a)
2
1.5
1
0.5 0 0.5 1 1.5 2
5
4
3
2
1
0
1
2
3
x(t)
v(t)
(b)
