Balakumar Balachandran, Magrab E.B. Vibrations
Подождите немного. Документ загружается.


−2
0
2
H(0.2) 1.04
→
x
ss
(t)2%
x(t)/(F
o
/k)
−2
0
2
H(0.2) 1.04
→
x
ss
x(t)/(F
o
/k)
0 40 80
(a)
(b)
120 160 200
−2
0
2
H(0.2) 1
→
x
ss
t
x(t)/(F
o
/k)
−20
0
20
H(1) 10
→
x
ss
x(t)/(F
o
/k)
−5
0
5
H(1) 2.5
→
x
ss
x(t)/(F
o
/k)
0 20 40 60 80 100
−1
0
1
H(1) 0.714
→
x
ss
t
x(t)/(F
o
/k)
N
d
1.47, 0.05
N
d
0.37, 0.2
N
d
0.12, 0.7
N
d
12.5, 0.05
N
d
3.13, 0.2
N
d
0.966, 0.7
(t)2%
(t)2%
(t)2%
(t)2%
(t)2%
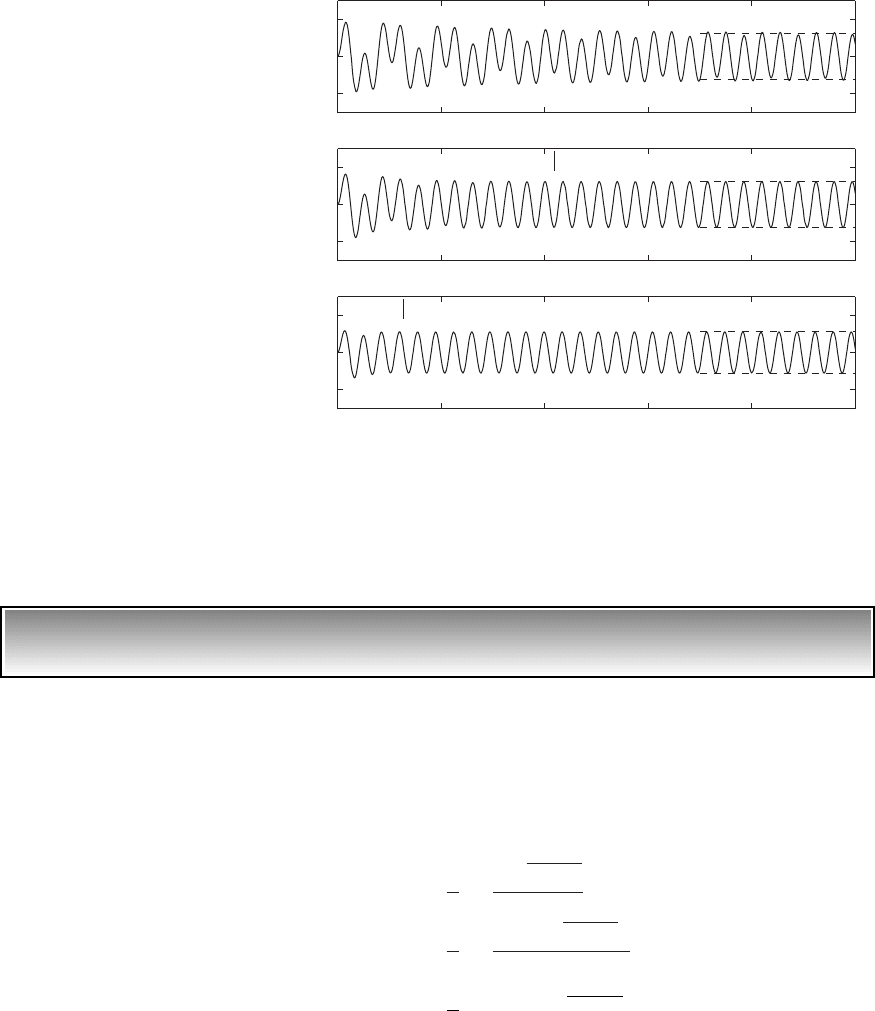
FIGURE 5.4
Response of a system to a suddenly applied cosine wave forcing function when the transient
envelope parameter d 0.02 and for different values of z: (a) 0.2 and (b) 1.0.
EXAMPLE 5.1 Estimation of system damping ratio to tailor transient response
A single degree-of-freedom system with a natural frequency of 66.4 rad/s is
intermittently cycled on and off. When it is on, it vibrates at 5.8 Hz. What
should the damping ratio be in order for the system to decay to within 5% of
its steady-state amplitude in 150 ms each time that the forcing is applied?
Assuming that the system settles down to the rest state in between the
forcing cycles, from Eq. (5.10b), which is applicable when the forcing is
turned on, we have that
Solving numerically
5
, we obtain z 0.244.
9.96
1
z
ln 30.0911 21 z
2
4
166.4 210.15 2
1
z
ln c
0.0521 z
2
12p 5.82/66.4
d
t
d
v
n
t
d
1
z
ln c
d21 z
2
d
5.2 Response to Harmonic Excitation 191
0.2
0.2
0.2
0
0.2
H(3) 0.125
x(t)/(F
o
/k)
0
0.2
H(3) 0.124
→
x
ss
x(t)/(F
o
/k)
0 12 24
(
c
)
36 48 60
0
0.2
H(3) 0.111
→
x
ss
t
x(t)/(F
o
/k)
N
d
47.9, 0.05
N
d
12, 0.2
N
d
3.65, 0.7
(t)2%
(t)2%
FIGURE 5.4 (continued )
(c) 3.0.
5
The MATLAB function fzero was used.

192 CHAPTER 5 Single Degree-of-Freedom Systems Subjected to Periodic Excitations
6
The MATLAB function ode45 was used.
EXAMPLE 5.2 Start up response of a flexibly supported rotating machine
When a rotating machine starts from rest, the rotation speed usually increases
linearly until it reaches its operating speed v
s
at t t
o
. Then, from
Figure 5.5, we see that the excitation frequency of the machine can be ex-
pressed as
(a)
Then, for the system shown in Figure 5.6, the forcing on the inertia element
of the system is
(b)
or
(c)
where
s
v
s
/v
n
is the ratio of the final rotational speed of the machine to
the natural frequency of the system, t v
n
t, and t
o
v
n
t
o
2pt
o
/T
n
is
proportional to the ratio of the time it takes to reach the operating speed to the
period of undamped free oscillation of the system.
Then, the system shown in Figure 5.6 is governed by Eq. (3.23), which is
(d)
where the over dot denotes the derivative with respect to the nondimensional
time t. Because of the form of the argument of the sine function, this equa-
tion has to be solved numerically
6
for x(t)/(F
o
/k). The results are shown in
Figure 5.7 for z 0.1 and for all combinations of
s
0.25, 1.0, and 2, and
t
o
/2p 0.25, 1.0, 2.0. At each value of
s
, the corresponding steady-state re-
sponse is given by Eqs. (5.17) and (5.18); that is, H(
s
) and u(
s
).
The results shown in Figure 5.7 have transient characteristics during an
initial phase that is followed by a steady-state phase, as seen in Figure 5.3.
When the final value of the excitation frequency is lower than the natural fre-
quency, the steady-state amplitude is not much different from the maximum
amplitude of the transient motions. However, when the final value of the ex-
citation frequency is equal to the natural frequency, a build up from the tran-
sient motions to the steady-state motions is noticeable. When the final value
of the excitation frequency is higher than the excitation frequency, it is seen
that the transients decay to the final steady-state motions.
5.2.2 Excitation Present for All Time
In the previous section, it was shown that for a harmonic periodic excitation
initiated at time t 0, the response of the vibratory system consists of a
x
$
2zx
#
x
F
o
k
sin 1
s
t
2
/t
o
3u1t2 u1t t
o
24
s
tu1t t
o
22
f 1t2 F
o
sin 1
s
t
2
/t
o
3u1t2 u1t t
o
24
s
tu1t t
o
22
F
o
sin 1v
s
1t
2
/t
o
23u1t2 u1t t
o
24 v
s
tu1t t
o
22
f 1t 2 F
o
sin 1v
e
1t 2t 2
v
e
1t 2 v
s
1t/t
o
23u1t2 u1t t
o
24 v
s
u1t t
o
2
FIGURE 5.5
Excitation frequency ramped up to
its operating frequency v
s
at time t
o
.
FIGURE 5.6
Single degree-of-freedom system
subjected to an excitation whose
frequency v
e
(t) ramps up from zero
to the operating frequency v
s
.
e
s
t
o
t
m
F
o
sin(
e
(t)t)
kc
transient part and a steady-state part. After a nondimensional time t
d
, only the
steady-state part of the response remains. This observation is taken advantage
of to characterize linear systems in terms of frequency-response functions and
transfer functions. Once a frequency-response function is determined for a
linear vibratory system from a harmonic forcing, this frequency-response
function can be used to determine the response of a linear vibratory system
for any combination of harmonic inputs. In order to proceed in this direction,
first, the previously determined results for the steady-state portion of the re-
sponse found in Section 5.2.1 are revisited.
When the periodic forcing is given by
f(t) F
o
sin(vt) (5.16a)
or equivalently, in terms of the nondimensional time variable t,as
f(t) F
o
sin(t) (5.16b)
that is, the harmonic excitation is present for all time, the associated steady-
state portion of the response is given by Eqs. (5.8) and (5.9). Thus,
(5.17)
Steady-state Steady-state
amplitude phase
x
ss
1t 2
F
o
k
H12sin 1t u122
5.2 Response to Harmonic Excitation 193
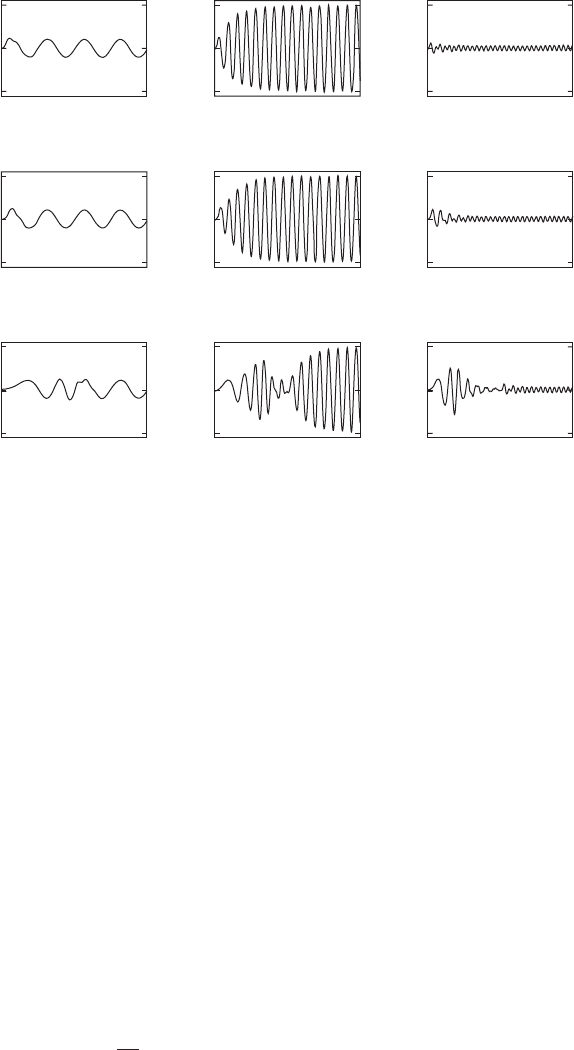
FIGURE 5.7
Response of a single degree-of-freedom system to an excitation whose frequency ramps up
from zero to a final nondimensional frequency
s
.
⎫
⎬
⎭
⎫
⎬
⎭
5
0
0
5
50
x()/(F
o
/k)
o
/8,
s
0.25, H(
s
) 1.07
100
5
0
0
5
50
x()/(F
o
/k)
o
/8,
s
1, H(
s
) 5
100
5
0
0
5
50
x()/(F
o
/k)
o
/8,
s
2, H(
s
) 0.33
o
,
s
0.25, H(
s
) 1.07
o
,
s
1, H(
s
) 5
o
,
s
2, H(
s
) 0.33
100
5
0
0
5
50
x()/(F
o
/k)
100
5
0
0
5
50
x()/(F
o
/k)
100
5
0
0
5
50
x()/(F
o
/k)
100
5
0
0
5
50
x()/(F
o
/k)
100
5
0
0
5
50
x()/(F
o
/k)
100
5
0
0
5
50
x()/(F
o
/k)
100
o
8,
s
0.25, H(
s
) 1.07
o
8,
s
1, H(
s
) 5
o
8,
s
2, H(
s
) 0.33

where
(5.18)
The steady-state velocity and steady-state acceleration are, respectively,
given by
(5.19)
We see that for harmonic oscillations, the magnitude of the acceleration is
equal to the square of the excitation frequency times the displacement mag-
nitude and the acceleration response is 180° out of phase with the displace-
ment response. The magnitude of the velocity is equal to the excitation fre-
quency times the magnitude of the displacement and the velocity response is
90° out of phase with the displacement response.
EXAMPLE 5.3
Forced response of a damped system
Consider the electric motor shown in Figure 5.8a. The output of the motor is
connected to two shafts whose opposite ends are fixed. The motor provides
a harmonic drive torque directed along the direction of the unit vector k.
This torque has a magnitude M
o
100 N m and the driving frequency
v is 475 rad/s. The rotary inertia of the electric motor J
o
is 0.020 kg m
2
,
the torsional stiffness of the shafts are k
t1
2500 N m/rad and k
t2
3000 N m/rad, and the overall damping experienced by the rotor can be
a
ss
1t 2
d
2
x1t 2
dt
2
a
F
o
v
n
2
k
b
2
H12sin 1t u122
2
v
2
n
x 1t2
a
F
o
v
n
k
bH12sin 1t u12 p/2 2
v
ss
1t 2
dx1t 2
dt
a
F
o
v
n
k
bH12cos 1t u122
u12 tan
1
2z
1
2
H12
1
2D12
1
211
2
2
2
12z2
2
194 CHAPTER 5 Single Degree-of-Freedom Systems Subjected to Periodic Excitations
FIGURE 5.8
(a) Electric motor driven restrained by two shafts and (b) free-body diagram.
(b)(a)
k
t1
k
t2
k
t1
k
t2
kk
J
o
C
t
J
o
M
o
cos (t)
.
..

quantified in terms of a torsional damper with the damping coefficient c
t
1.25 N m s/rad. We shall determine the form of the steady-state response
and the amplitude and the phase of the steady-state response.
The governing equation of the motor is derived based on the principle
of angular momentum balance. Consider the free-body diagram shown in
Figure 5.8b, which includes the inertial moment . The principle of an-
gular momentum applied to the center of the motor leads to the following
governing equation
(a)
Dividing Eq. (a) by the rotary inertia J
o
, we obtain the following equation
whose form is similar to Eq. (5.1)
(b)
where the system natural frequency and damping factor are given by,
respectively,
(c)
Based on Eq. (5.17), the solution of Eq. (b) for steady-state motion is
given by
(d)
where the nondimensional excitation frequency v /v
n
and the non-
dimensional time t v
n
t. For the given parameter values, the calculations
lead to the following:
(e)u12
tan
1
a
2 0.06 0.91
1 0.91
2
b 0.57 rad
H12
1
211 0.91
2
2
2
12 0.06 0.912
2
4.91
v
v
n
475 rad/s
524.40 rad/s
0.91
z
1.25 N
#
m
#
s/rad
2 0.020 kg
#
m
2
524.40 rad/s
0.06
v
n
B
5500 N
#
m/rad
0.020 kg
#
m
2
524.40 rad/s
k
t1
k
t2
5500 N
#
m/rad
f
ss
1t 2
M
o
k
t1
k
t2
H12cos 1t u122
z
c
t
2J
o
v
n
v
n
B
k
t1
k
t2
J
o
f
$
2zv
n
f
#
v
2
n
f
M
o
J
o
cos 1vt 2
J
o
f
$
c
t
f
#
1k
t1
k
t2
2f M
o
cos 1vt 2
J
o
f
$
k
5.2 Response to Harmonic Excitation 195

Hence, from the values provided in Eqs. (e), the steady-state response of the
electric motor given by Eq. (d) is written as
(f)
Thus, the amplitude of the harmonic steady-state motion is 0.09 rad at a fre-
quency of 475 rad/s, and the phase lag relative to the excitation is 0.57 rad.
5.2.3 Response of Undamped System and Resonance
When a linear vibratory system is undamped, z 0, the governing equation
given by Eq. (5.1), reduces to
(5.20)
Response When v v
n
(1)
For the excitation given by Eq. (5.3), and for zero initial conditions, the re-
sponse is determined from Eqs. (5.7) and (5.8) with z 0. Thus, we obtain
(5.21a)
or, equivalently,
(5.21b)
which is valid when the excitation frequency is different from the natural
frequency; that is, when 1 (or v v
n
). It is clear from the form of
Eqs. (5.21) that for an undamped system excited by a sinusoidal forcing at a
frequency that is not equal to the natural frequency, the response consists of a
frequency component at the excitation frequency v and a frequency compo-
nent at the natural frequency v
n
. Unless the ratio of v/v
n
is a rational number,
the displacement response is not periodic.
Response When v v
n
(1)
The response of an undamped system when 1, is obtained from Eq. (5.6)
with z 0 and 1. Thus, we arrive at
(5.22)
Evaluating the integral in Eq. (5.22) results in
(5.23)x 1t 2
F
o
2k
5sin 1t 2 tcos 1t 26
x1t 2
F
o
k
t
0
sin 1t j 2sin 1j 2dj
x1t 2
F
o
k11
2
2
5
sin 1vt 2 sin 1v
n
t26
x1t 2
F
o
k11
2
2
5
sin 1t2 sin 1t26
d
2
x
dt
2
v
2
n
x
f 1t 2
m
0.09
cos 1475t 0.57 2 rad
f
ss
1t 2
100 N
#
m
5500 N
#
m/rad
4.91
cos 1475t 0.57 2
196 CHAPTER 5 Single Degree-of-Freedom Systems Subjected to Periodic Excitations

The displacement response is not periodic, because the amplitude of the sec-
ond term in Eq. (5.23) increases as time increases.
Resonance and Stability of Response
For the case where 1, the response of the undamped system given by
Eq. (5.21) always has a finite magnitude, since sin(t) and sin(t) have finite
values for all time. Thus, it follows that
(5.24)
where A is a positive finite number. Hence, for 1, an undamped system
excited by a finite harmonic excitation is stable in the sense of boundedness
introduced in Section 4.3. However, this is not true when 1. When
1, the term tcos(t) in Eq. (5.23) grows linearly in amplitude with time
and, hence, it becomes unbounded after a long time. This special ratio 1
(v v
n
) is called a resonance relation; that is, the linear system given by
Eq. (5.20) is said to be in resonance when the excitation frequency is equal to
the natural frequency.
From a practical standpoint, the question of boundedness is important.
Since there is always some amount of damping in a system, it is clear from
Eqs. (5.7) to (5.9) that the response remains bounded when excited at the nat-
ural frequency; that is, for 1
(5.25)
The response given by Eq. (5.25) satisfies the boundedness condition given
by Eq. (5.24), even though as the damping decreases in magnitude the re-
sponse increases in magnitude.
EXAMPLE 5.4
Forced response of an undamped system
Consider translational motions of a vibratory system with a mass of 100 kg
and a stiffness of 100 N/m. When a harmonic forcing of the form F
o
sin(vt)
acts on the mass of the system, where F
o
1.0 N, we shall determine the re-
sponses of the system and plot them for the following cases: i) v 0.2 rad/s,
ii) v 1.0 rad/s, and iii) v 2.0 rad/s.
Let the variable x be used to describe the translation of the mass. Then,
from Eq. (5.20),
(a)
The natural frequency of the system is
(b)v
n
B
k
m
B
100 N/m
100 kg
1 rad/s
x
$
v
2
n
x
F
o
m
sin 1vt 2
lim
t씮 q
x1t 2
F
o
2zk
sin 1t p/2 2
0x1t 20 A
t 0
5.2 Response to Harmonic Excitation 197
Hence, for Cases i and iii, the excitation frequency is different from the natu-
ral frequency, and for Case ii, the excitation frequency is equal to the natural
frequency of the system.
In Cases i and iii, the solution for the displacement response is given by
Eq. (5.21); that is,
(c)
On the other hand, in Case ii, the response is given by Eq. (5.23); that is,
(d)
For the given values, the responses are as follows:
Case i
(e)
Case ii
(f)
Case iii
(g)
The graphs of Eqs. (e), (f), and (g) are provided in the Figure 5.9. From the
graphs, it is clear that the response of the undamped system remains bounded
when the excitation frequency is away from the natural frequency, as in
Cases i and iii. However, in Case ii, the response becomes unbounded after a
long period of time, since the amplitude increases with time.
5.2.4 Magnitude and Phase Information
In the case of an undamped linear vibratory system, there is a phase shift of
180° in the response as one goes from an excitation frequency that is less than
the natural frequency to an excitation frequency that is greater than the natu-
ral frequency. This can be discerned from Eq. (5.21) by noting that the change
in sign is brought about by the term 1
2
.
For a linear damped vibratory system excited at the resonance frequency
1, the response lags the excitation by 90° as shown by Eq. (5.25) and in
0.003 5sin 12t2 2sint6
m
x1t 2
1 N
100 N/m 11 10.2/1.0 2
2
2
5
sin 12t 2 10.2/1.02sin 1t 26
0.005 5sin t t cos t6
m
x1t 2
1 N
2 100 N/m
5sin
t t cos t6
0.015sin 10.2t2 0.2 sin t6
m
x1t 2
1 N
100 N/m 11 10.2/1.0 2
2
2
5sin
10.2t 2 10.2/1.02sin 11 t26
x1t 2
F
o
2k
5sin 1v
n
t2 v
n
t cos 1v
n
t26
x1t 2
F
o
k11
2
2
5sin
1vt 2sin 1v
n
t26
198 CHAPTER 5 Single Degree-of-Freedom Systems Subjected to Periodic Excitations
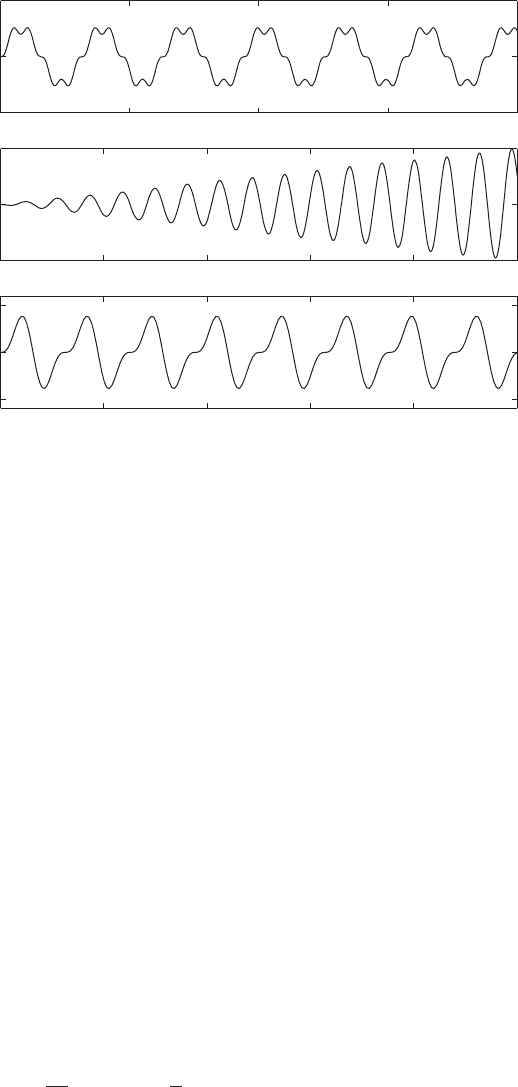
Figure 5.2b. This observation is used in experiments to determine if the exci-
tation frequency is equal to the undamped natural frequency of the system;
that is, v v
n
. The magnitude of the response is also large at v v
n
(1) when z is small.
Response Characteristics in Different Excitation Frequency Ranges
Additional characteristics of the response of an underdamped, linear vibra-
tory system can be determined by examining the steady-state response x
ss
(t)
in the frequency ranges 1 and 1 and at the frequency location
1; that is, in a region considerably below the natural frequency, in a re-
gion well above the natural frequency, and at the natural frequency, respec-
tively. The examination is performed by studying the values of H() and
u() in these three ranges.
1 In this region, Eqs. (5.18) lead to
H() → 1
u() → 0 (5.26)
and, therefore, from Eq. (5.17), we obtain
(5.27)x
ss
1t 2
F
o
k
sin 1t2
1
k
f 1t2
5.2 Response to Harmonic Excitation 199
FIGURE 5.9
Displacement response of an undamped system subjected to harmonic forcing at three
frequencies: i) v 0.2 rad/s; ii) v 1.0 rad/s; and iii) v 2.0 rad/s.
0 50 100 150 200
0.02
0.01
0.5
0
0.02
v
0.2 rad/s
x(t)
0 20 40 60 80 100
0
0.5
v
1.0 rad/s
x(t)
0 10 20 30 40 50
0
0.01
v
2.0 rad/s
x(t)
t (s)
