Balakumar Balachandran, Magrab E.B. Vibrations
Подождите немного. Документ загружается.


where F
a
m
o
Pv
2
is the magnitude of the applied (unbalanced) force, and
(5.62b)
Rewriting Eq. (5.62a) in terms of the nondimensional time t v
n
t, we
have
(5.63a)
where
(5.63b)
Displacement Response
Making use of Eq. (5.17), we see that the steady-state solution to Eq. (5.63a) is
x(t) M
P
H
ub
()sin(t u()) (5.64)
Displacement Phase
magnitude
where the amplitude response H
ub
() and the phase response u() are
given by
(5.65)
Comparing the forms of the amplitude response and the phase response
given by Eqs. (5.65) for the system with the rotating unbalanced mass to those
given by Eqs. (5.18) for the system with direct excitation acting on the mass,
it is seen that the phase responses are the same and the amplitude responses
are different. These similarities and differences can be further seen by com-
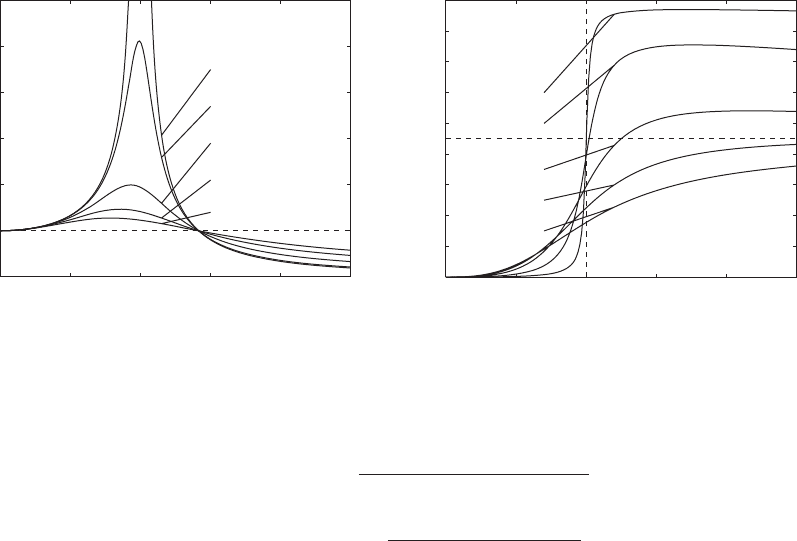
paring the graphs of the amplitude response and phase response of the unbal-
anced system shown in Figure 5.22 with those for direct excitation of the mass
shown in Figure 5.2.
Velocity and Acceleration Responses
The velocity and acceleration responses are determined from the displace-
ment response given by Eq. (5.64) to be, respectively,
(5.66)a1t 2
d
2
x1t 2
dt
2
M
P
2
H
ub
1 2sin 1t u122
2
x1t 2
v1t 2
dx1t 2
dt
M
P
H
ub
1 2cos 1t u122
u12 tan
1
2z
1
2
H
ub
1 2
2
H12
2
211
2
2
2
12z2
2
M
P
m
o
P
m
d
2
x
dt
2
2z
dx
dt
x f 1t2 M
P
2
sin 1t2
m M m
o
and
v
n
B
k
m
220 CHAPTER 5 Single Degree-of-Freedom Systems Subjected to Periodic Excitations
⎫
⎬
⎭
⎫
⎬
⎭

We see that for harmonic oscillations, the magnitude of the acceleration is
equal to the square of the frequency ratio times the magnitude of the dis-
placement and that the acceleration response lags the displacement response
by 180°.
Response Characteristics in Different Excitation Frequency Ranges
The solution is examined in detail in the frequency ranges 1 and
1 and the frequency location 1. This examination is performed by
studying H
ub
() and u() given by Eqs. (5.65) in these three ranges.
1 In this region, we find that Eqs. (5.65) simplify to
H
ub
() →
2
u() → 0 (5.67)
and, therefore, the displacement response given by Eq. (5.64) simplifies to
x(t) M
P
2
sin(t) f(t) (5.68)
where we have used the fact that f(t) M
P
2
sin(t). Thus, the displace-
ment response is in phase with the unbalanced force f(t).
The velocity response is determined from Eq. (5.68) to be
v(t) M
P
3
cos(t) M
P
3
sin(t p/2) (5.69)
The velocity response leads the displacement response by p/2; that is, the
maximum value of the velocity occurs before the maximum value of the dis-
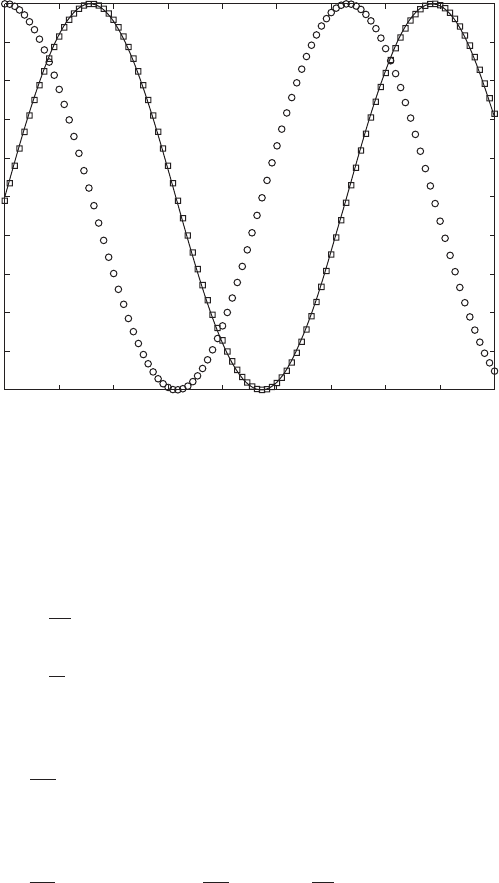
placement. These results are illustrated in Figure 5.23.
5.4 Systems with Rotating Unbalanced Mass 221
(a) (b)
0 0.5 1 1.5 2 2.5
0
1
2
3
4
5
6
Ω
H
ub
(Ω)
z 0.02
z 0.1
z 0.3
z 0.5
z 0.7
0 0.5 1 1.5 2 2.5
0
20
40
60
80
100
120
140
160
180
Ω
u(Ω) (deg)
z 0.02
z 0.02
z 0.1
z 0.3
z 0.5
z 0.7
FIGURE 5.22
Harmonic excitation due to rotating unbalance: (a) amplitude response and (b) phase response.
1 For this value of , we find from Eqs. (5.65) that
(5.70)
and, therefore, the displacement response given by Eq. (5.64) reduces to
(5.71)
The velocity response follows from Eq. (5.71), and it is given by
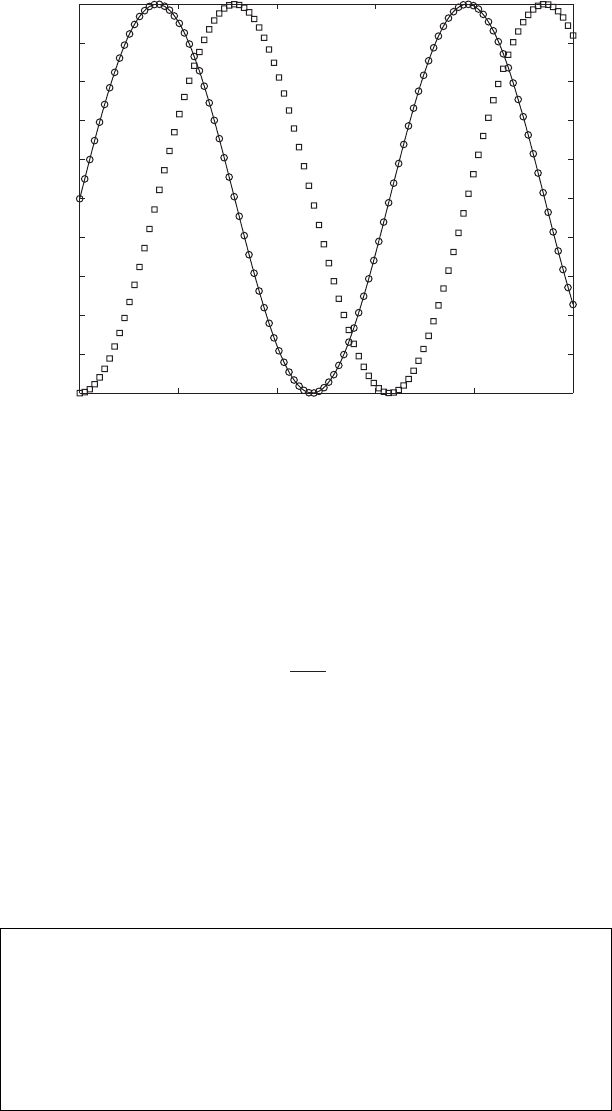
(5.72)
where we used the fact that f(t) M
P
2
sin(t) and 1. Therefore, in
this region, the velocity response is in phase with the unbalanced force. These
results are illustrated in Figure 5.24.
1 In this region, we find from Eqs. (5.65) that
H
ub
() → 1
u() → p (5.73)
v1t 2
M
P
2z
cos 1t p/2 2
M
P
2z
sin 1t2
1
2z
f 1t2
x1t 2
M
P
2z
sin 1t p/2 2
u11 2
p
2
H
ub
11 2
1
2z
222 CHAPTER 5 Single Degree-of-Freedom Systems Subjected to Periodic Excitations
0 10 20 30 40 50 60 70 80 90
1
0.8
0.6
0.4
0.2
0
0.2
0.4
0.6
0.8
1
Ωt
Amplitude
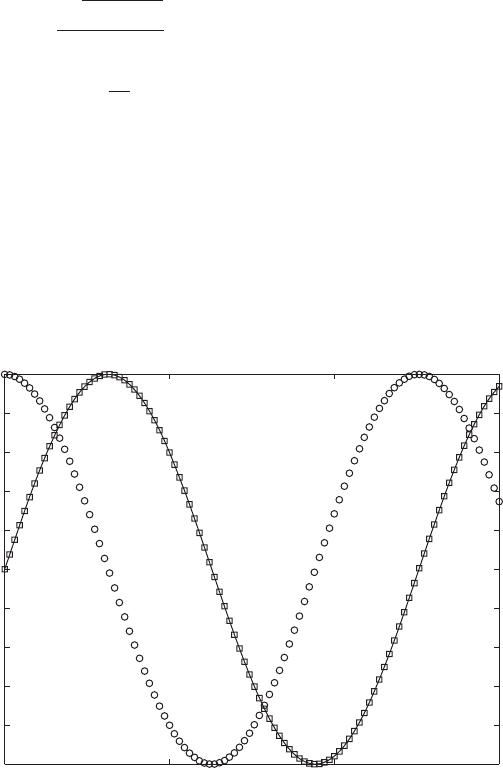
FIGURE 5.23
Phase relationships among displacement, velocity, and force of system with unbalance for
1 and z 0.1. [— f(t)/(M
P
2
); 䊐 x(t)/(M
P
2
); 䊊 v(t)/(M
P
3
).]
The fact that the amplitude response converges to unity can also be seen from
Figure 5.22a. Therefore, the displacement response is approximated from
Eq. (5.64) as
(5.74)
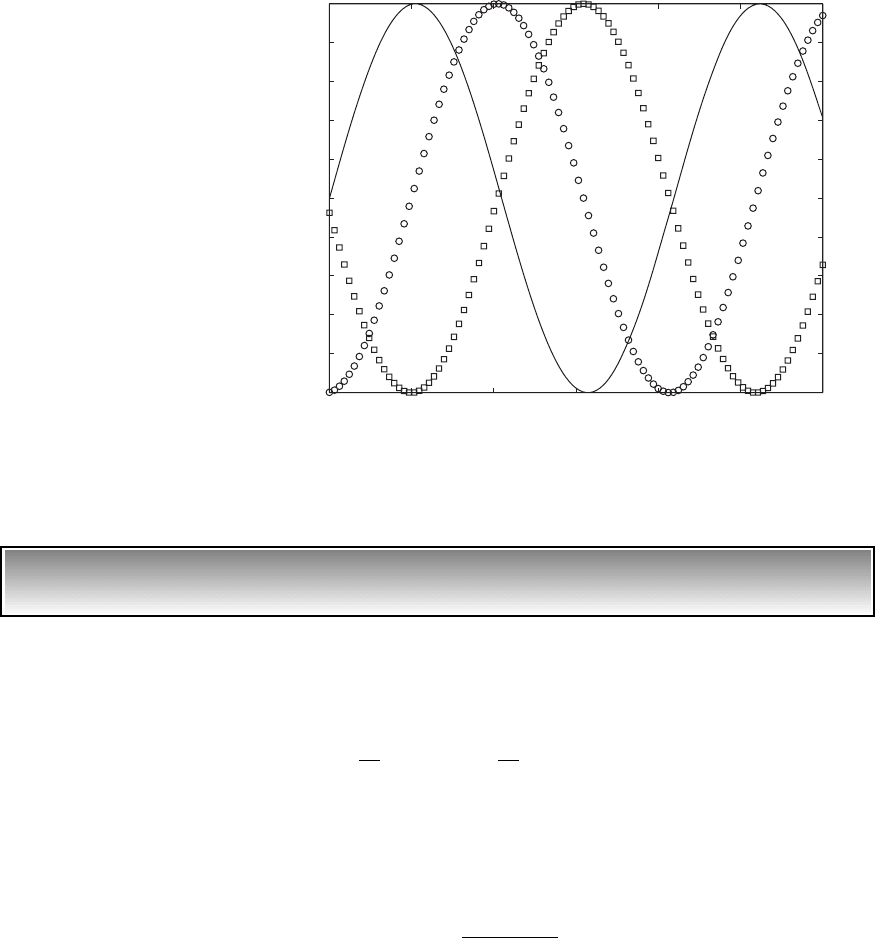
Thus, the displacement is 180° out of phase with the applied force. The cor-
responding velocity response is determined from Eq. (5.74) to be
v(t) M
P
cos(t p) M
P
sin(t p/2) (5.75)
Therefore, in this region the velocity lags the force by p/2. These results are
shown in Figure 5.25. Based on the discussion provided in this section and the
graphs shown in Figure 5.22, the following design guideline is proposed.
x1t 2 M
P
sin 1t p 2
f 1t2
2
5.4 Systems with Rotating Unbalanced Mass 223
0 2 4 6 8 10
1
0.8
0.6
0.4
0.2
0
0.2
0.4
0.6
0.8
1
Ωt
Amplitude
FIGURE 5.24
Phase relationships among displacement, velocity, and force of system with unbalance for
1 and z 0.1. [— f(t)/M
P
; 䊐 x(t)/(M
P
/(2z)); 䊊 v(t)/(M
P
/(2z)).]
Design Guideline: In order to reduce the displace.ment of the mass
of a single degree-of-freedom system when the mass is subjected to a
harmonic unbalanced force, one choice is for the natural frequency of
the system to be at least twice the excitation frequency or 50% lower
than the excitation frequency. These ranges hold irrespective of the sys-
tem’s damping for 0 z 1.
EXAMPLE 5.7 Fraction of applied force that is transmitted to the base
We shall determine the frequency at which a specified fraction of the magni-
tude of the applied force F
a
due to an unbalanced mass is transmitted to the
base. The fraction is denoted by g, where g 1. The magnitude of the trans-
mitted force F
T
is determined from Eq. (3.10) and Figure 3.1 to be
(a)
Substituting Eq. (5.64) into Eq. (a), we obtain
11
(b)
where we have used Eq. (D.12) and introduced the amplitude and phase
(c)
respectively.
w
tan
1
2z
F
1
kM
P
H
ub
1 221 12z 2
2
F
1
sin 1t u12 w2
F
T
kM
P
H
ub
1 232z cos 1t u122 sin 1t u1224
F
T
c
dx
dt
kx k c2z
dx
dt
x d
224 CHAPTER 5 Single Degree-of-Freedom Systems Subjected to Periodic Excitations
0 0.5 1 1.5 2 2.5 3
1
0.8
0.6
0.4
0.2
0
0.2
0.4
0.6
0.8
1
Ωt
Amplitude
FIGURE 5.25
Phase relationships among displacement, velocity, and force of system with unbalance for
1 and z 0.1. [— f(t)/(M
P
2
); 䊐 x(t)/M
P
; 䊊 v(t)/(M
P
).]
11
It is noticed that the transmitted force is at the same frequency as the excitation produced by the
rotating unbalance. This captures the transmission force characteristics observed in many indus-
trial applications. However, there are other machines for which the nonharmonic nature of the ex-
citation due to the rotating unbalance becomes important. See Bachmann et al., ibid.
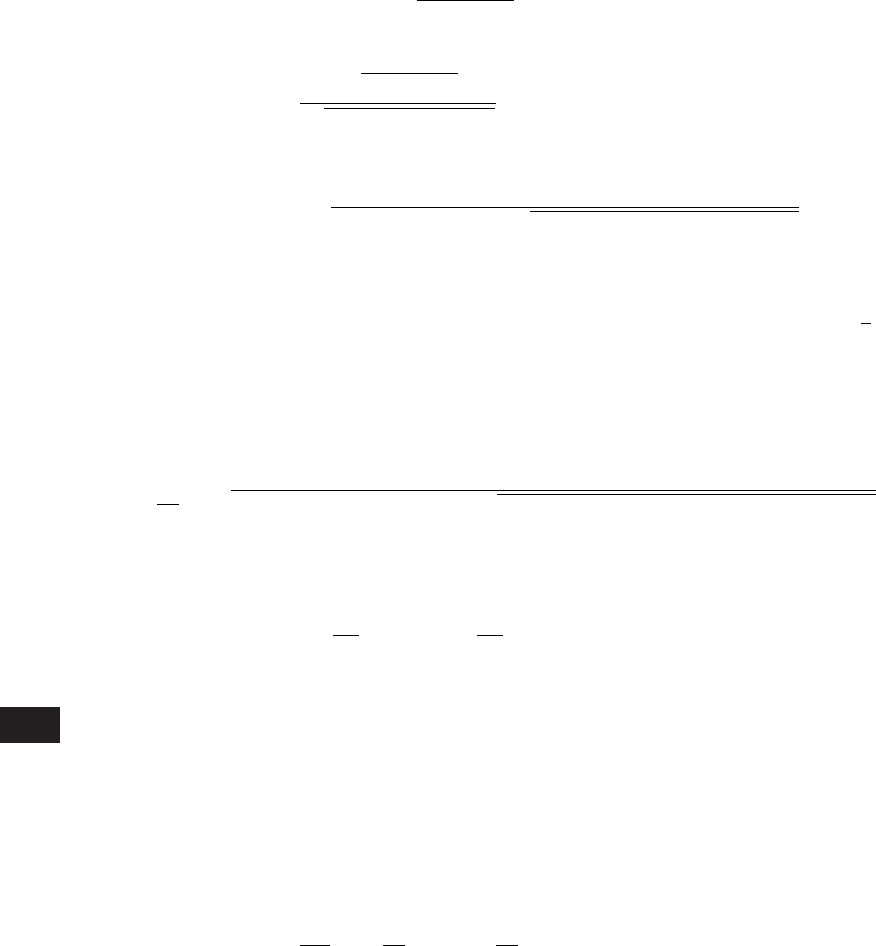
To determine the frequency at which the magnitude of the force trans-
mitted to the base is a fraction g of the applied force F
a
, we require that
F
1
gF
a
,or
(d)
Therefore, making use of Eqs. (5.62b), (5.63b), and (5.65), we obtain
(e)
Solving for the real positive value of the nondimensional excitation frequency
from Eq. (e), we arrive at
(f)
We shall see in the next section that g, as represented by Eq. (e), is sim-
ply the magnitude of the frequency-response function obtained when a har-
monic excitation is applied to the base of the system. When g 1,
which is the frequency ratio above which the magnitude of the unbalanced
force that is transmitted to the base is less than F
a
.
Let us assume that the system has a natural frequency of 35 Hz and determine
the angular speed of the rotating mass so that only 15% of the unbalanced force is
transmitted to the base when the damping ratio is 0.1. Then, from Eq. (f )
Since there are 2p rad/rev and 60 s/min, the required angular speed is
5.5 SYSTEMS WITH BASE EXCITATION
The base excitation model is useful for studying buildings subjected to
earthquakes, packaging during transportation, and for designing accelerom-
eters. The equation describing the motion of a single degree-of-freedom
system with a vibrating base, which is shown in Figure 3.6, is given by
Eq. (3.28). Rewriting Eq. (3.28) in terms of the nondimensional time t
v
n
t,wehave
(5.76)
where it is recalled that x(t) is the displacement response of the mass and y(t)
is the displacement of the base. If the base motion is harmonic—that is,
y(t) y
o
sin(t) (5.77)
d
2
x
dt
2
2z
dx
dt
x 2z
dy
dt
y
N
60
2p
v 2.953 v
n
60
2p
2.953160 2f
n
2.953160 2135 2 6200 rpm
2.953
v
v
n
21 210.12
2
11 10.152
2
2 1
11 210.1 2
2
11 10.152
2
22
2
1 10.15 2
2
12,
0 g 1
21 2z
2
11 g
2
2 1
11 2z
2
11 g
2
22
2
1 g
2
21 12z2
2
211
2
2
2
12z2
2
g
kM
P
H
ub
1 221 12z 2
2
gm
o
Pv
2
5.5 Systems with Base Excitation 225

then Eq. (5.76) becomes
(5.78)
Displacement Response
The right-hand side of Eq. (5.78) contains forcing functions of the form given
by Eq. (5.12) and (5.3). Thus, the solution to Eq. (5.78) is determined from
Eqs. (5.8a), (5.15a), and (D.12) to be
(5.79)
where u() is given by the second of Eqs. (5.65) and
(5.80)
By using the appropriate trigonometric identities,
12
we can rewrite Eq. (5.79) as
x(t) y
o
H
mb
()sin(t c()) (5.81)
Displacement Phase
magnitude
where the amplitude response H
mb
() and the phase response c() are
given by
(5.82)
The graphs of the amplitude response and the phase response are shown in
Figure 5.26 for different damping factors. As seen in Figure 5.26, the curves
obtained for the different damping factors all have the same amplitude value
at .
Velocity and Acceleration Responses
The velocity and acceleration are determined from Eq. (5.81) to be,
respectively,
(5.83)
The relative displacement of the mass to the base is determined from
Eqs. (5.77) and (5.81) to be
(5.84) y
o
X
y
1 2sin 1t w
b
1 22
y
o
35H
mb
1 2cos 1c122 16sin 1t2 H
mb
1 2sin 1c122cos 1t 24
z x1t 2 y1t2 y
o
3H
mb
1 2sin 1t c122 sin 1t 24
a1t 2
2
v
2
n
x1t 2
v1t 2 y
o
v
n
H
mb
1 2cos 1t c122
12
c12 tan
1
2z
3
1
2
14z
2
12
H
mb
1 2
21 12z2
2
211
2
2
2
12z2
2
w tan
1
2z
x1t 2 y
o
H1221 12z 2
2
sin 1t u12 w2
d
2
x
dt
2
2z
dx
dt
x 2z y
o
cos 1t2 y
o
sin 1t2
226 CHAPTER 5 Single Degree-of-Freedom Systems Subjected to Periodic Excitations
12
tan
1
x tan
1
y tan
1
x y
1 xy
⎫
⎬
⎭
⎫
⎬
⎭
where the amplitude function X
y
() and the phase function w
b
() are given by
(5.85)
and Eq. (D.12) has been used. A plot of X
y
() versus the frequency ratio is
identical to that obtained for the amplitude response H
ub
() of system with an
unbalanced mass, which is shown in Figure 5.22a. However, the interpreta-
tion is different. For 0.3, the mass and base move in phase and almost as
a rigid body. When 2, the mass moves very little; that is, it is relatively
stationary, and only the base is moving. When 1, the mass magnifies the
motion of the base and there is large relative movement of the mass with re-
spect to the base.
Response Characteristics in Different Excitation Frequency Ranges
We now examine the system response in the frequency ranges 1 and
1, and the frequency location 1. This examination is carried out
by studying H
mb
() and c() in these three ranges.
1 In this region, we find from Eqs. (5.82) that
(5.86)
and, hence, the displacement response given by Eq. (5.81) simplifies to
x(t) y
o
sin(t) y(t) (5.87)
c12씮 0
H
mb
1 2씮 1
w
b
1 2 tan
1
H
mb
1 2sin 1c122
H
mb
1 2cos 1c122 1
X
y
1 2 2H
2
mb
2H
mb
cos 1c122 1
5.5 Systems with Base Excitation 227
0 0.5 1 1.5 2 2.5
0
20
40
60
80
100
120
140
160
180
Ω
C(Ω) (deg)
0 0.5 1 1.5 2 2.5
0
1
2
3
4
5
6
Ω
H
mb
(Ω)
z 0.02
z 0.1
z 0.3
z 0.5
z 0.7
z 0.02
z 0.1
z 0.3
z 0.5
z 0.7
(a) (b)
FIGURE 5.26
Excitation due to moving base: (a) amplitude response and (b) phase response.
Hence, in this frequency region, the displacement of the mass is approxi-
mately equal to the displacement of the base. The corresponding velocity is
determined from Eq. (5.87) to be
v(t) y
o
v
n
cos(t) y
o
v
n
sin(t p/2) (5.88)
Thus, the velocity response leads the displacement response by p/2. These
results are shown in Figure 5.27.
1 In this region, we determine from Eqs. (5.82) that
(5.89)
From Eq. (5.89), it is seen that the phase angle at 1 is a function of z. It
follows from Eq. (5.81) that the displacement response is
x(t) y
o
H
mb
(1)sin(t c(1)) (5.90)
and the corresponding velocity response is
v(t) y
o
v
n
H
mb
(1)cos(t c(1)) (5.91)
These results are shown in Figure 5.28.
c11 2 tan
1
1
2z
H
mb
11 2
21 12z 2
2
2z
228 CHAPTER 5 Single Degree-of-Freedom Systems Subjected to Periodic Excitations
0 50 100 150
1
0.8
0.6
0.4
0.2
0
0.2
0.4
0.6
0.8
1
Ωt
Amplitude
FIGURE 5.27
Phase relationships among displacement, velocity, and force of system with moving base
when 1 and z 0.1. [— y(t)/y
o
; 䊐 x(t)/y
o
; 䊊 v(t)/(y
o
v
n
).]

1 In this region, Eqs. (5.82) simplify to
(5.92)
and, therefore, the displacement response given by Eq. (5.81) is approxi-
mated to
(5.93)
The velocity response follows from Eq. (5.93), and it has the form
v(t) y
o
v
n
2z cos(t c
1
()) (5.94)
These results are shown in Figure 5.29. Based on the discussion provided in
this section and Figure 5.26, the following design guidelines are postulated.
x1t 2
2zy
o
sin 1t c
1
1 22
c12씮 c
1
1 2 tan
1
2z
4z
2
1
H
mb
1 2씮
2z
5.5 Systems with Base Excitation 229
0 2 4 6 8 10
1
0.8
0.6
0.4
0.2
0
0.2
0.4
0.6
0.8
1
Ωt
Amplitude
FIGURE 5.28
Phase relationships among displacement, velocity, and force of system with moving base
when 1 and z 0.1. [— y(t)/y
o
; 䊐 x(t)/(y
o
H
mb
(1)); 䊊 v(t)/(y
o
v
n
H
mb
(1)).]
Design Guideline: In order to reduce the displacement of the mass of
a single degree-of-freedom system when the base is subjected to har-
monic excitation, one choice is for the natural frequency of the system
to be at least 30% lower than the excitation frequency.
