Balakumar Balachandran, Magrab E.B. Vibrations

Подождите немного. Документ загружается.

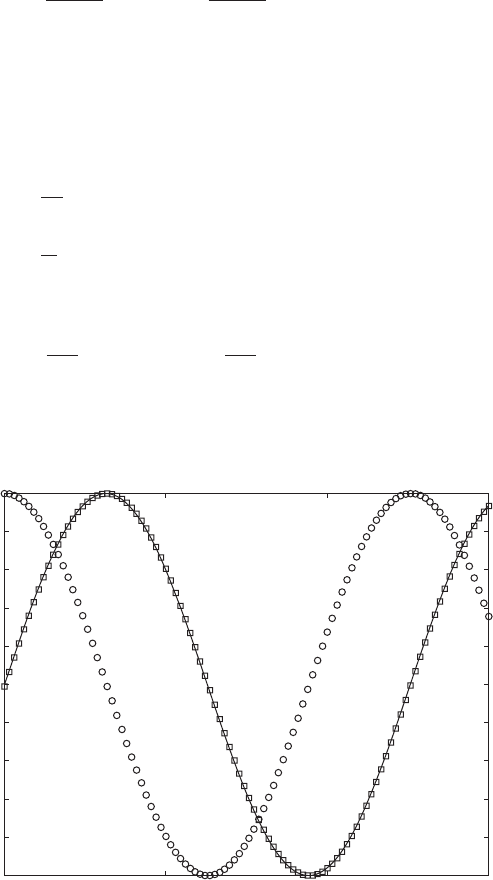
Since the only system parameter that determines the displacement response is

the stiffness k, we call this region the stiffness-dominated region. In this re-

gion, the displacement is in phase with the force.

The velocity response is determined from Eq. (5.27) to be

(5.28)

Therefore, as expected, the velocity response leads the displacement response

by p/2; that is, the maximum value of the velocity occurs before the maxi-

mum value of the displacement. These results are illustrated in Figure 5.10.

1 At this value of , Eqs. (5.18) simplify to

(5.29)

Therefore, the displacement response given by Eq. (5.17) takes the form

(5.30)

Thus, for a given excitation amplitude F

and natural frequency v

, the am-

plitude of the displacement is determined by the damping coefﬁcient c. This

1t 2

2kz

sin 1t  p/2 2

sin 1t  p/2 2

u11 2

H11 2

1t 2

v

cos 1t2

v

sin1t  p/2 2

200 CHAPTER 5 Single Degree-of-Freedom Systems Subjected to Periodic Excitations

FIGURE 5.10

Phase relationships among displacement, velocity, and force in the stiffness-dominated

region: 1. [— f(t)/F

; 䊐 x(t)/(F

/k); 䊊 v (t)/(v

/k).]

0 50 100 150



0.8



0.6



0.4



0.2

0.4

0.6

0.8

Ωt

Amplitude

region, therefore, is called the damping-dominated region. We also see that

the displacement lags the force by p/2 and that this phase lag is independent

of z. For z  0, it is mentioned that H() is not a maximum when 1. We

shall determine this maximum value and the value of  at which it occurs

subsequently. The amplitude response is characterized by a peak close to the

natural frequency for values of z in the range 0  z  0.3, as can be seen from

Figure 5.2a.

The velocity response is obtained from Eq. (5.30) to be

(5.31)

Therefore, in this region, the velocity is in phase with the force. These results

are illustrated in Figure 5.11.

  1 In this region, the amplitude and phase responses given by

Eqs. (5.18) simplify to

(5.32)

and, therefore, the displacement response given by Eq. (5.17) simpliﬁes to

(5.33)x

1t 2

sin 1t  p 2

sin 1t2

f 1t2

u12씮 p

H12씮





1t 2

2kz

cos 1t  p/2 2

sin 1t2

f 1t2

5.2 Response to Harmonic Excitation 201

FIGURE 5.11

Phase relationships among displacement, velocity, and force in the damping-dominated

region: 1. [— f (t)/F

; 䊐 x(t)/(F

/(2zk)); 䊊 v(t)/(F

/c).]

0 1 2 3 4 5 6 7 8 9 10

1

0.8

0.6

0.4

0.2

0.2

0.4

0.6

0.8

Ωt

Amplitude

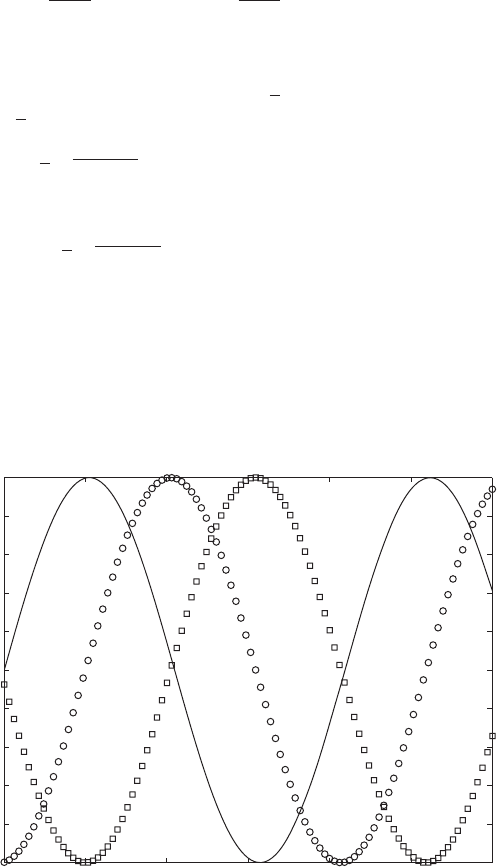
Thus, the displacement response is 180° out of phase with the applied force.

For a given f(t), the amplitude of the displacement is inversely proportional

to m, the mass. This region, therefore, is called the inertia-dominated region.

The velocity is determined from Eq. (5.33) to be

(5.34)

Hence, in this region, the velocity lags the force by p/2. These results are

shown in Figure 5.12.

It can be shown that when for 0, and when

H()  1 for

These response characteristics can also be seen in Figure 5.2.

The dependence of the system response on the different system parame-

ters is summarized as a function of the excitation frequency as shown in Fig-

ure 5.13. Further discussion about the response magnitude and the response

phase as a function of the excitation frequency is provided in Section 5.3.

v  v

1221  2z

12 21  2z

z  1/ 12,

z  1/ 12

, H12 1

1t 2

k

cos 1t  p 2

k

sin 1t  p/2 2

202 CHAPTER 5 Single Degree-of-Freedom Systems Subjected to Periodic Excitations

FIGURE 5.12

Phase relationships among displacement, velocity, and force in the inertia-dominated region:

1. [— f(t)/F

; 䊐 x(t)/(F

/(k

)); 䊊 v(t)/(F

/(k)).]

0 0.5 1 1.5 2 2.5 3



0.8



0.6



0.4



0.2

0.4

0.6

0.8

Ωt

Amplitude

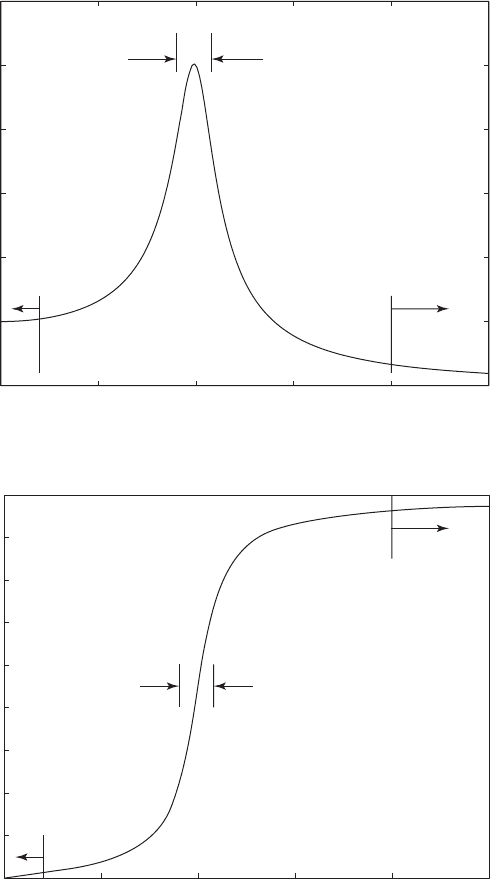
FIGURE 5.13

Three regions of a single degree-of-freedom system: (a) amplitude response and

(b) phase response.

0 0.5 1 1.5 2 2.5

(a)

(b)

Inertia

dominated

x(t)~1/m

Stiffness

dominated

x(t)~1/k

Damping

dominated

x(t)~1/c

Ω

H(Ω)

180

160

140

120

100

0 0.5 1 1.5

Damping

dominated

t)~1/c

Stiffness

dominated

t)~1/k

Inertia

dominated

t)~1/m

2 2.5

Ω

u (Ω) (deg)

5.3 FREQUENCY-RESPONSE FUNCTION

5.3.1 Introduction

In Section 5.2, the responses of undamped and underdamped systems to har-

monic excitations were discussed and the notions of resonance of a linear vi-

bratory system, steady-state motion, and frequency-response function were

introduced. In this section, the concept of a frequency-response function is

further treated.

As illustrated in Figure 5.14, for a linear vibratory system, a frequency-

response function provides a relationship between a system’s input and a sys-

tem’s output. The frequency-response function G() is a complex-valued

function of frequency, and this function provides information about the mag-

nitude and phase of the steady-state response of a linear vibratory system as

a function of the excitation frequency.

204 CHAPTER 5 Single Degree-of-Freedom Systems Subjected to Periodic Excitations

Frequency-response function

of a system G(Ω)

Force input

Displacement

output

FIGURE 5.14

Conceptual illustration of the frequency-response function.

Observations

Stiffness-dominated region: When the amplitude of the harmonic ex-

citing force is constant and the excitation frequency is much less than

the natural frequency of the system, the magnitude of the displacement

is determined by the system’s stiffness. The displacement response is

in phase with the excitation force.

Damping-dominated region: When the amplitude of the harmonic ex-

citing force is constant and the excitation frequency equals the natural

frequency of the system, the magnitude of the displacement response is

magniﬁed for 0  z  1, and the amount of magniﬁcation is deter-

mined by the system’s damping coefﬁcient. The displacement response

lags the excitation force by 90°.

Inertia-dominated region: When the amplitude of the harmonic excit-

ing force is constant and the excitation frequency is much greater than

the natural frequency of the system, the magnitude of the displacement

response is determined by the system’s inertia. When  is greater than

, the magnitude of the amplitude response is always less than 1.

The displacement response is almost 180° out of phase with the excita-

tion force.

1/ 12

For the cases treated in Section 5.2, one can deﬁne the frequency-response

function G() in terms of the force input and displacement output of the linear

vibratory system. In its general representation, this function has the form

(5.35)

where v/v

is the ratio of the excitation frequency v to the natural

frequency of the system v

, k is the stiffness of the vibratory system, the

nondimensional function H() provides the magnitude, and u()

is the phase lag associated with the response. In Eq. (5.35), the frequency-

response function has dimensions of displacement/force; that is, m/N. If the

frequency-response function is desired in nondimensional form, it is deﬁned as

(5.36)

where the complex-valued function is now nondimensional.

For a linear vibratory system, where the forcing is applied to the mass di-

rectly as in Figure 5.1, the nondimensional function H() and the phase u()

are given by Eqs. (5.8). These functions have different forms when the exci-

tation is either applied to the base or the source of the excitation is a rotating

unbalance, as discussed in Sections 5.4 and 5.5, respectively.

Based on Eqs. (5.8) and (5.35), the magnitude of the frequency-response

function is given by

(5.37)

As evident from Eq. (5.37), this function contains information about the sys-

tem parameters such as the stiffness k, and the system characteristics such as

the natural frequency v

and the damping factor z. In Section 5.3.2, we dis-

cuss how the frequency-response function magnitude can be curve-ﬁt to ex-

tract information about the characteristics of a linear vibratory system. In Sec-

tion 5.3.3, the sensitivity of the frequency-response function magnitude to

different system parameters is examined, and in Section 5.3.4, the relation-

ship between a frequency-response function and a transfer function is ex-

plained. Finally, in Section 5.3.5, we discuss alternative forms of the fre-

quency response function.

5.3.2 Curve Fitting and Parameter Estimation

Let us suppose that one conducts an experiment where a sinusoidal forcing is

applied to a system. After the motions of the system reach steady state, that is,

after many cycles of forcing, the forcing and displacement are measured by us-

ing appropriate transducers. From these measured quantities, one can deter-

mine the ratio of the displacement magnitude to the force magnitude. If this ex-

periment is repeated at different frequencies over a frequency range, and if at

each excitation frequency this ratio is determined, the resulting information

0G120

H12



k211 

 12z2

1 2

 H1 2e

ju12

1 2 kG12

j  11

G12

H12e

ju12

5.3 Frequency-Response Function 205

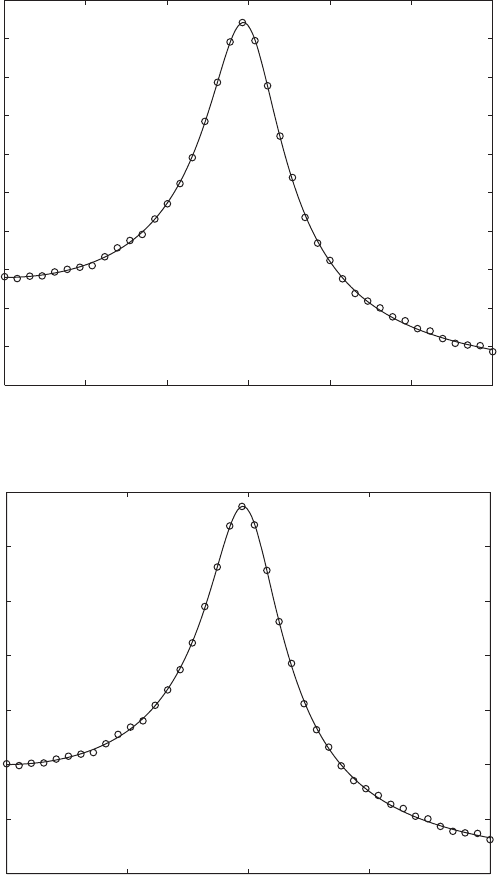
(a)

(b)

0 0.5 1 1.5 2

0.5

1.5

2.5

3.5

(v/1.5)

H(v)

0 0.5 1 1.5 2 2.5 3

0.005

0.01

0.015

0.02

0.025

0.03

0.035

0.04

0.045

0.05

|G(v)|

FIGURE 5.15

Model identiﬁcation using Eq. (5.37): (a) experimental data along with identiﬁed model 0G(v) 0

and (b) experimental data along with identiﬁed model H()  k 0G(v) 0.

can be plotted as a function of frequency as shown in Figure 5.15a where the

open circles represent the experimental data. We assume that the physical sys-

tem of interest is a linear vibratory system and use Eq. (5.1) to describe the sys-

tem. Then, based on Eq. (5.37), one can curve-ﬁt the experimental data and

estimate the values of the stiffness k, the natural frequency v

, and the damping

factor z. For the data shown in Figure 5.15a, it is found

that z  0.15, v



1.5 rad/s, and k  71.5 N/m. These values were inserted in Eq. (5.37) to obtain

the solid line passing through the data. In Figure 5.15b, the nondimensional

function H()  k 0G(v)0is shown along with the experimental data.

In Figure 5.16, the nondimensional function H() is plotted on a graph

with a logarithmic scale for the frequency axis and a logarithmic scale for the

magnitude axis. This type of graph helps highlight the location of a resonance

and the overall response characteristics as a function of frequency over several

decades of frequency. In such log-log plots, the magnitude is expressed in terms

of decibels (dB), which is discussed in Appendix C.

The frequency-response function provides an alternate means to the

logarithmic-decrement method given in Section 4.2.3, which was based on

free-oscillation data for estimating the damping factor in a vibratory system

model. In addition, as discussed in Section 5.3.1, and later in Chapter 6, the

frequency-response function of a vibratory system also can be determined for

force inputs other than sinusoidal excitations.

5.3 Frequency-Response Function 207

The MATLAB function lsqcurveﬁt from the Optimization Toolbox was used.

0.1 1 10

40

30

20

10

H(Ω) (dB)

Ω

FIGURE 5.16

Logarithmic plot of H().

5.3.3 Sensitivity to System Parameters and

Filter Characteristics

In this section, we illustrate how the sensitivity of a mechanical system’s re-

sponse to an applied forcing is determined and how a mechanical system can

be viewed as a ﬁlter. The notions of sensitivity and ﬁlters are important for the

design of many mechanical systems, in particular, sensors used for vibration

measurements.

Sensitivity

The amplitude response of a single degree-of-freedom system can be used to

determine the response sensitivity. The system’s sensitivity is deﬁned as the

ratio of the change in the displacement to a change in the applied force. Thus,

when 1, we ﬁnd from Eq. (5.27) that the sensitivity as determined by

the response magnitude and force magnitude is

(5.38)

where x and F represent the changes in the response and force magnitudes,

respectively. Let us suppose that the parameters c and m are held constant and

that we consider two systems, one with a spring constant k

and another with

a spring constant k

. Then, the sensitivity for the ﬁrst system is

(5.39)

Let

(5.40)

Furthermore, we have the following expressions for the corresponding natural

frequencies, static displacements, and damping factors of the two systems:

(5.41)

Then, from Eqs. (5.17) and (5.18), the sensitivity S

for the modiﬁed sys-

tem is given by

(5.42a)S

 `

¢x

¢F

`

211  a



 12a

2



21k

 z



21k

st2



 a

st1



st1



 0



S  `

¢x

¢F

`

208 CHAPTER 5 Single Degree-of-Freedom Systems Subjected to Periodic Excitations

where the frequency ratio v/v

. For 1, Eq. (5.42a) is approxi-

mated as

(5.42b)

Equation (5.42a) is plotted in Figure 5.17 for a

 1. We see from this

ﬁgure and from Eqs. (5.41) that as the sensitivity increases, the natural fre-

quency of the system decreases (and the static displacement increases) and

the damping ratio increases. This tradeoff between sensitivity and the location

of the natural frequency is important in the design of vibration sensors, where

a frequent desire is to have a device with a high sensitivity and a high natural

frequency.

This discussion presents a broader view of the ideas presented in

Example 3.7, where only the inﬂuence of the different system parameters on

z was discussed.



 a

5.3 Frequency-Response Function 209

 1/k

 a



/√a

z

√a

Sensitivity

Frequency

FIGURE 5.17

Effect of change in sensitivity with respect to the natural frequency and damping ratio

when c and m remain constant: a

 k

 0.

Design Guideline: If c and m are held constant and the stiffness of a

single degree-of-freedom system is changed from k

to k

, then the re-

sponse sensitivity of the system changes from S

to k

and the

damping ratio changes from z

to z

See, for example: S. Valoff and W. J. Kaiser, “Presettable Micromachined MEMS Accelerome-

ters,” 12th IEEE International Conference on Micro Electrical Mechanical Systems, Orlando, FL,

pp. 72–76, (January 1999); and A. Partridge, et al., “A High-Performance Planar Piezoresistive

Accelerometer,” J. Microelectromechanical Systems, Vol. 9, No. 1, pp. 58–65 (March 2000).