Balakumar Balachandran, Magrab E.B. Vibrations

Подождите немного. Документ загружается.

The relative displacement is

(d)

and, after substituting Eq. (d) into Eq. (c), we arrive at

(e)

If we set t  v

t, then Eq. (e) can be written as

(f)

For the displacement to the base of the system, we assume a step-like dis-

turbance that has variable rise time and a rounded shape given by

(g)

This waveform was selected instead of a unit step function, in part, because

its higher order derivatives are continuous. The normalized waveform

y(t)/y

max

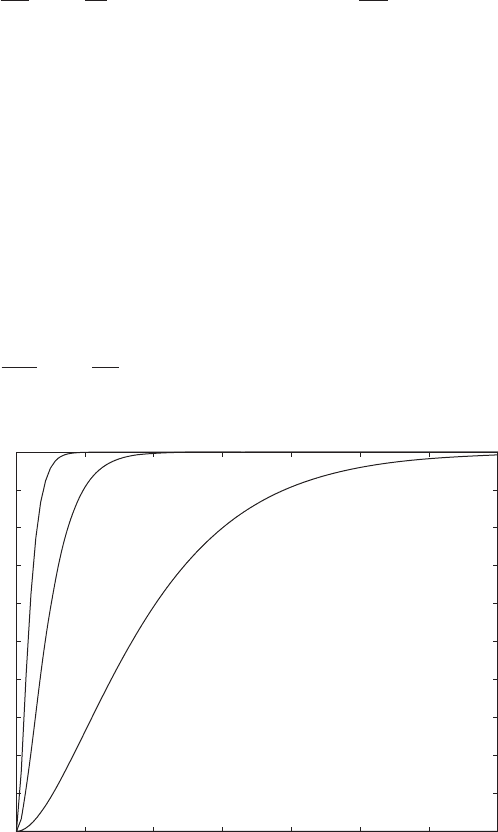
is shown in Figure 6.31 for several values of the parameter g. Tak-

ing the second derivative of Eq. (g) with respect to t, we arrive at

(h)

We now substitute Eq. (h) into Eq. (f) and introduce the nondimensional

variable z

(t)  z(t)/y

max

to obtain

(i)

 2z

 z

 a

 d

a

 g1t 2

1t 2 y

max

11  gt2e

gt

y1t 2 y

max

31  11  gt2e

gt

 2z

 z  a1z  d

ad



 cz

 kz  ka1z  d

kad

 my

z1t 2 x1t 2 y1t 2

330 CHAPTER 6 Single Degree-of-Freedom Systems Subjected to Transient Excitations

0 1 2 3 4 5 6 7

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9



x(t)/y

max

FIGURE 6.31

Base excitation waveform for several values of g.

6.7 Response to Half-Sine Wave Pulse 331

The MATLAB function ode45 was used.

where and

(j)

The absolute displacement x(t) is obtained from Eq. (d) and Eq. (g); that is,

(k)

where z

(t) is a solution of Eq. (i).

The numerical evaluation

of Eq. ( j) yields the results shown in Figure

6.32 for a  30 and for a  0; that is, when the nonlinear spring is replaced

by a linear spring. In addition, we have selected the nondimensional static

displacements of and The value corresponds to thed

 0d

 0.d

 0.3

x1t2 y

max

1t 2 y

max

31  11  gt2e

gt

g1t 2g

11  gt2e

gt

 ay

max

 d

max

1.8

1.6

1.4

1.2

0.8

0.6

0.4

0.2



)/y

max



)/y

max

(a)



15 20 25

 

1.8

1.6

1.4

1.2

0.8

0.6

0.4

0.2



)/y

max



)/y

max

(b)



15 20 25

 

1.8

1.6

1.4

1.2

0.8

0.6

0.4

0.2



)/y

max



)/y

max

(c)



15 20 25

 

1.8

1.6

1.4

1.2

0.8

0.6

0.4

0.2



)/y

max



)/y

max

(d)



15 20 25

 

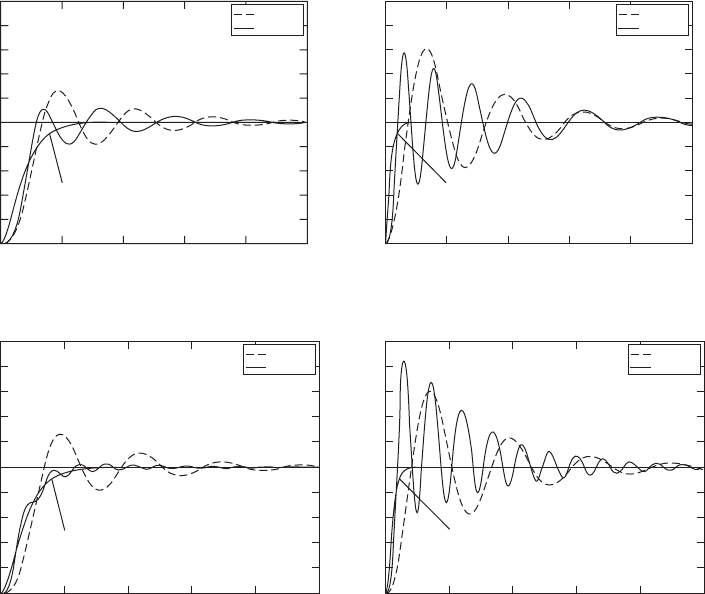
FIGURE 6.32

Normalized absolute displacement of the mass of a single degree-of-freedom system with a nonlinear spring

with z  0.15 and subject to the base excitation shown in Figure 6.31: (a) d

 0 and g  1, (b) d

 0 and g  4,

 0.3 and g  1, and (d) d

 0.3 and g  4.

332 CHAPTER 6 Single Degree-of-Freedom Systems Subjected to Transient Excitations

case of no static displacement; that is, when the system is positioned as shown

in Figure 6.1. We see that combination of the linear spring and the nonlinear

spring is stiffer than the linear spring by itself and, therefore, the period of the

oscillation is shorter than that of the linear spring by itself, especially as the

rise time decreases (g increases). In addition, as the rise time of the input dis-

placement decreases (g increases), the overshoot increases, which is similar

to what was found for the response to a ramp input applied to a linear single

degree-of-freedom system.

6.8 IMPACT TESTING

Impact testing is performed with standard shock test machines where a test

object impacts a stationary platform. Placing different materials of different

geometry between the object and its rigid terminating platform alters the

shape of the impact proﬁle.

These inserts are called programmers. These

programmers are typically elastomer discs, lead pellets, and sand. The ma-

chines fall into one of three categories: (1) free-fall machines, which includes

pendulum type machines; (2) pneumatic machines; and (3) electrodynamic

C. LaLanne, Mechanical Shock, Hermes Penton Ltd., Chapters 6 and 7, 2002.

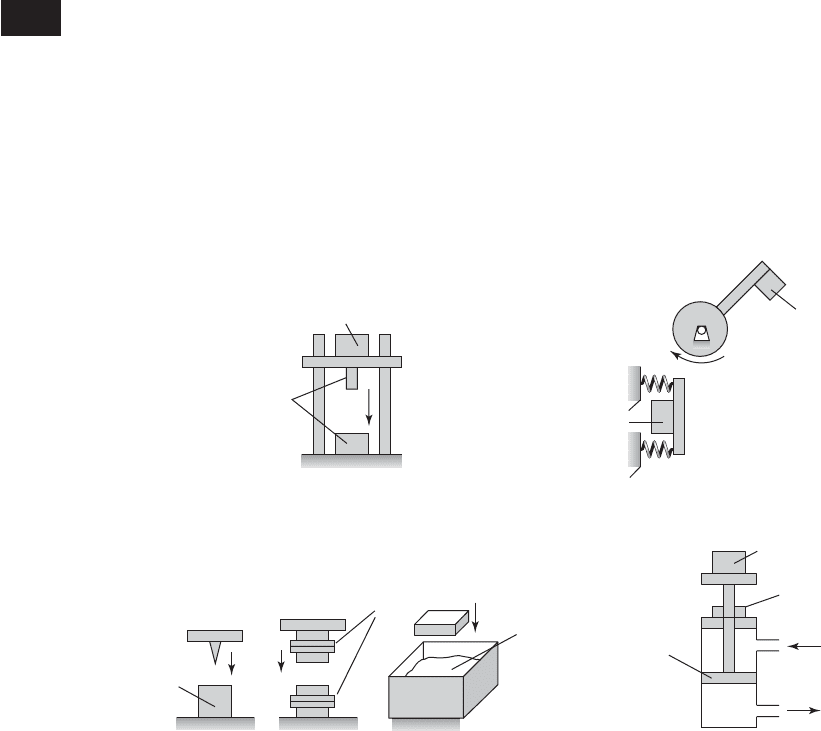
Sand

(programmer)

Elastomer

(programmer)

Lead

(programmer)

(c)

Programmer

Test object

(b)

Programmer

Test object

Guide

(a)

(d)

Programmer

Test object

Piston

Air in

Air out

FIGURE 6.33

Different impact testing methods and the locations of their programmers: (a) free-fall apparatus, (b) pendulum, (c) different

programmers, and (d) pneumatic machine.

Exercises 333

machines. In free-fall machines, the object's velocity is a function of the re-

lease height from the impact platform. In pneumatic machines, the pneumatic

driver produces the object’s velocity. In electrodynamic shakers (recall Ex-

ample 5.10), the shock spectrum is attained by tailoring the time-varying

shape, magnitude, and duration of the signal sent to the shaker or by specify-

ing the input spectrum. Schematic drawings of these different types of

machines are given in Figure 6.33. One application of impact testing is in

determining the efﬁcacy of motorcycle helmets, where the acceleration re-

sponse to impact is required to determine the head injury criteria (HIC) for

these devices.

Another application

of impact analysis is to reduce the

amount of force that is transferred to the ground (soil) in manufacturing fa-

cilities that use drop forges and other heavy machinery that create intermit-

tent loads.

6.9 SUMMARY

In this chapter, responses of single degree-of-freedom systems subjected to

various types of transient excitations have been studied. A common charac-

teristic of the systems studied is that the excitation provides a “sudden”

change to the state of the system. The notion of the impulse response, which

is an important component for determining the response of linear systems, has

been introduced, along with such notions as settling time and rise time of the

response. It was also illustrated as to how the response to an input excitation

with an arbitrary frequency spectrum can be determined.

EXERCISES

Section 6.2

6.1 Determine the response of a vibratory system

governed by the following equation:

Assume that m  1 kg, the initial conditions are

x(0)  0.1 m and m/s, and the excitation fre-

quency v  1.4 rad/s. Plot the response.

10 2 0

 1.5 sin1vt 2u1t2 4d1t  3 2

1t 2 0.2x

1t 2 3.5x1t2

6.2 Consider the following single degree-of-freedom

system excited by two impulses when the system is

initially at rest

Determine the displacement response of this vibratory

system and plot the response.

6.3 From extensive biomechanical tests, the spinal

stiffness k of a person is estimated to be 50,000 N/m.

1t 2 2x

1t 2 4x 1t 2 d1t 2 d1t  52

R. Willinger, et al., “Dynamic Characterization of Motorcycle Helmets: Modeling and Cou-

pling with the Human Head,” J. Sound Vibration, 235(4), pp. 611–615, 2000.

See, for example, A. G. Chehab and M. El Naggar, “Response of block foundations to impact

loads,” Journal of Sound and Vibration, 276 (2004) pp. 293–310.

334 CHAPTER 6 Single Degree-of-Freedom Systems Subjected to Transient Excitations

Assume that the body mass is 80 kg. Let us assume

that this person is driving an automobile without

wearing a seat belt. On hitting an obstacle, the driver

is thrown upwards, and drops in free fall onto an un-

padded seat and experiences an impulse with a mag-

nitude of Determine the resulting motions if

an undamped single degree-of-freedom model is used

to model the vertical vibrations of this person.

6.4 Determine the response of the vibratory system

discussed in Example 6.4 when the forcing due to the

wind spectrum is of the following form

where f is the frequency in Hz. Plot the result for the

values of k

given in Example 6.4.

Section 6.3

6.5 Determine the response of an underdamped single

degree-of-freedom system that is subjected to the

force Assume that the system is

initially at rest.

6.6 Repeat Example 6.5 when the step change in road

elevation a is 4 cm and the vehicle speed is 100 km/h.

Plot the results.

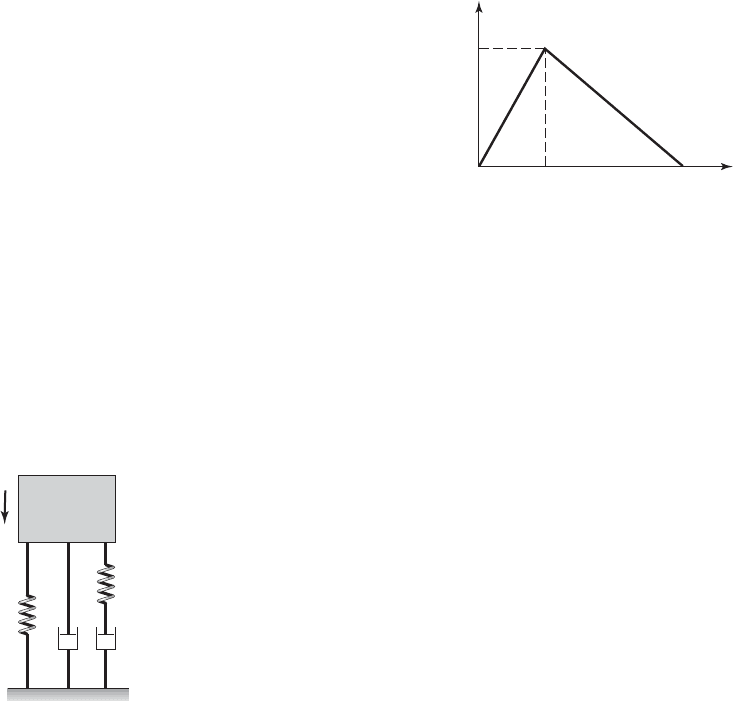
6.7 Refer to the Kelvin-Voigt-Maxwell combination

shown in Figure E6.7. Obtain an expression for the

displacement response in the Laplace transform do-

f 1t2 F

at

u1t 2.

0F1jf 20 200 fe

0.5f

100 N

main of the mass when the mass is subjected to a step-

function force of magnitude F

Section 6.4

6.8 A machine system of mass 30 kg is mounted on an

undamped foundation of stiffness 1500 N/m. During

the operations, the machine is subjected to a force of

the form shown in Figure E6.8, where the horizontal

axis time t is in seconds and the vertical axis is the am-

plitude of the force in Newtons. Assume that the ma-

chine system is initially at rest and determine the dis-

placement response of the system.

6.9 In Example 6.7, assume that the motions of the

slab ﬂoor are damped with the damping factor being

0.2. Determine the response of this damped system

for the forcing and system parameters given in Exam-

ple 6.7. Also, ﬁnd the earliest time at which the max-

imum displacement response occurs. Plot the results.

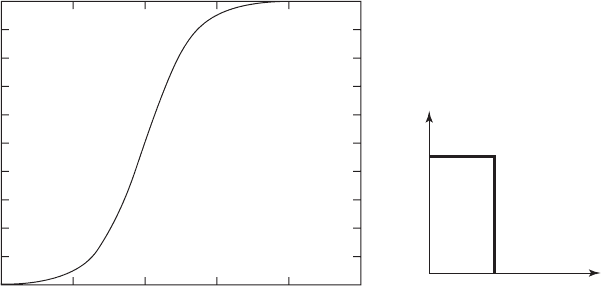
6.10 Consider the Boltzmann sigmoidal function,

whose general form is given by

where a, b, a, and t

are constants and S(t

, a, b, a, t

)

 a  b/2. This function can be used to create a step-

like function as shown in Figure E6.10 for S(t

,0,1,

60, 0.1). Determine the response of a system for f(t)

 F

S(t, 0, 1, 60, 0.1) and f(t)  F

S(t,0,1,6,1)and

graphically compare them to the response of the sys-

tem to the step input given by Eq. (6.23). The solu-

tions have to be obtained numerically.

S1t, a, b, a, t

2 a  b 11  e

a1t

t2

1

f(t)

0.5 s 2.0 s

2500 N

FIGURE E6.8

f(t)

FIGURE E6.7

Exercises 335

to the rectangular pulse shown in Figure E6.11. Plot

the displacement response for m  1 kg, z  0.1,

 4 rad/s, f

 1 N, and t

 1 s.

0.9

0.8

0.7

0.6

0.5

0.4

0.3

0.2

0.1

0 0.05 0.1

S()

0.15



0.2 0.25

FIGURE E6.10

FIGURE E6.11

Section 6.6

6.11 Determine the response of the damped second-

order system described by

1t 2 cx

1t 2 kx1t2 f 1t 2

Section 6.7

6.12 Plot the energy density and then determine the

bandwidth of the following pulse:

f 1t 2 0.5 11  cosv

t23u1t2 u1t  2p/v

f(t)

336

Many systems can vibrate in multiple directions. Such systems are described by models with multiple degrees-of-freedom. The cable

car and the locomotive can each simultaneously oscillate up and down as well as sway from left to right. (Source: © Zandebasenjis /

Dreamstime.com; Stockxpert.com)

337

Multiple Degree-of-Freedom Systems:

Governing Equations, Natural Frequencies,

and Mode Shapes

7.1 INTRODUCTION

7.2 GOVERNING EQUATIONS

7.2.1 Force-Balance and Moment-Balance Methods

7.2.2 General Form of Equations for a Linear Multi-Degree-of-Freedom System

7.2.3 Lagrange’s Equations of Motion

7.3 FREE RESPONSE CHARACTERISTICS

7.3.1 Undamped Systems: Natural Frequencies and Mode Shapes

7.3.2 Undamped Systems: Properties of Mode Shapes

7.3.3 Characteristics of Damped Systems

7.3.4 Conservation of Energy

7.4 ROTATING SHAFT ON FLEXIBLE SUPPORTS

7.5 STABILITY

7.6 SUMMARY

EXERCISES

7.1 INTRODUCTION

In Chapters 4 through 6, single degree-of-freedom systems and vibratory re-

sponses of these systems were studied. Systems with multiple degrees of

freedom and their responses are studied in this chapter and the next. Systems

that need to be described by more than one independent coordinate have mul-

tiple degrees of freedom. The number of degrees of freedom is determined by

the inertial elements present in a system. For example, in a system with two

degrees of freedom, there can be either one inertial element whose motion is

described by two independent coordinates or two inertial elements whose mo-

tions are described by two independent coordinates. In general, the number of

degrees of freedom of a system is not only determined by the inertial elements

present in a system, but also by the constraints imposed on the system. The

governing equations of motion of vibratory systems is determined by using

either force-balance and moment-balance methods or Lagrange’s equations.

In this chapter, both of these methods will be used to develop the system equa-

tions. Furthermore, viscous damping models will be used to model dissipa-

tion in the systems.

After developing the governing equations of motion, the determination

of the natural frequencies and mode shapes of multi-degree-of-freedom sys-

tems are examined at length. Forced oscillations are considered in the next

chapter. To describe the responses of single degree-of-freedom systems, only

time information is needed. In addition to the time information, one also

needs spatial information for describing the responses of systems with more

than one degree of freedom. This spatial information is expressed in terms of

mode shapes, which are determined from the free-vibration solution. Each

mode shape is associated with a natural frequency of the system. This shape

provides information about the relative spatial positions of the inertial ele-

ments in terms of the chosen generalized coordinates. Determination of mode

shapes and natural frequencies is discussed in detail in this chapter. As

illustrated in the next chapter, the spatial information obtained from the free-

vibration problem can also provide a basis for determining the forced re-

sponse of a system with multiple degrees of freedom. It is also shown there

that the properties of mode shapes can be used to construct the response of a

multi-degree-of-freedom system in terms of the responses of equivalent sin-

gle degree-of-freedom systems. This allows the use of the material presented

in the preceding chapters for determining the response of a system with mul-

tiple degrees of freedom.

The notions of stability introduced in Chapter 4 for single degree-of-

freedom systems are extended in this chapter to multi-degree-of-freedom

systems.

In this chapter, we shall show how to:

• Derive the governing equations for systems with multiple degrees of free-

dom by using force-balance and moment-balance methods.

• Derive the governing equations for systems with multiple degrees of free-

dom by using Lagrange's equations.

• Obtain the natural frequencies and mode shapes associated with vibra-

tions of systems with multiple degrees of freedom.

• Obtain the conditions under which the mode shapes are orthogonal.

• Interpret characteristics of damped systems.

• Determine the vibration characteristics of rotating shafts.

• Examine the stability of multiple degree-of-freedom systems.

7.2 GOVERNING EQUATIONS

In this section, two approaches are presented for determining the governing

equations of motion. The ﬁrst approach is based on force-balance and

moment-balance methods and the second approach is based on Lagrange’s

338 CHAPTER 7 Multiple Degree-of-Freedom Systems

equations. For algebraic ease, the number of degrees of freedom for the phys-

ical systems chosen in this chapter is less than or equal to ﬁve.

7.2.1 Force-Balance and Moment-Balance Methods

The underlying principles of the force-balance and moment-balance methods

are expressed by Eqs. (1.11) and (1.17), which relate the forces and moments

imposed on a system to the rate of change of linear momentum and the rate

of change of angular momentum, respectively.

7.2 Governing Equations 339

⎫

⎬

⎭

⎫

⎬

⎭

⎫

⎬

⎭

⎫

⎬

⎭

⎫

⎪

⎬

⎪

⎭

⎫

⎪

⎬

⎪

⎭

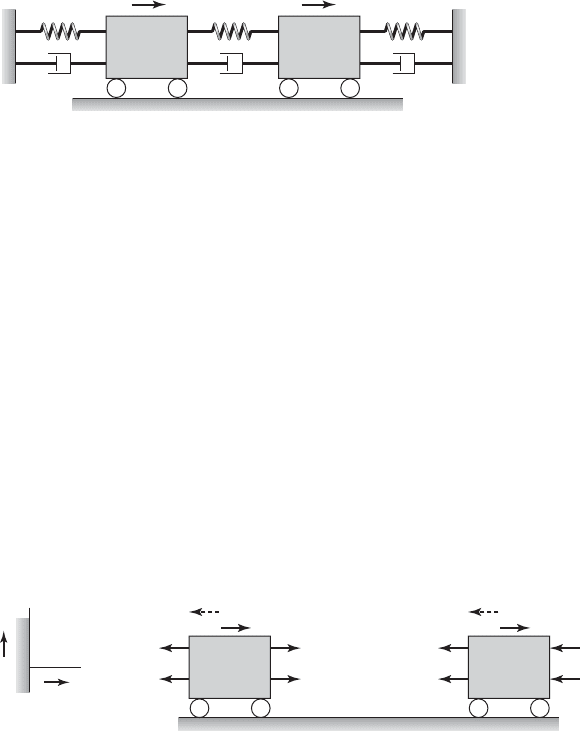
FIGURE 7.1

System with two degrees of freedom.

FIGURE 7.2

Free-body diagrams for masses m

and m

along with the respective inertial forces illustrated

by broken lines. The origin of the coordinate system is located on the ﬁxed boundary at the

left end of the spring.

, f

(t) x

, f

(t)

, f

 x

)

 x

)

, f

 x

)

 x

)

Force-Balance Method

To illustrate the use of force-balance methods, consider the system shown in

Figure 7.1. This system consists of linear springs, linear dampers, and trans-

lating inertia elements. The free-body diagrams for the point masses m

and

are shown, along with the respective inertial forces in Figure 7.2. The gen-

eralized coordinates x

and x

are used to specify the positions of the two

masses m

and m

, respectively, from the ﬁxed end on the left side. Based on

the free-body diagram of inertial element m

and carrying out the force bal-

ance along the horizontal direction i, one obtains the following equation:

External force

acting on

mass m

Force associated

with damper of

coefﬁcient c

Force associated

with damper of

coefﬁcient c

Force associated

with spring of

stiffness k

Force associated

with spring of

stiffness k

Inertia

force

m

k

k

 x

c

c

 x

f

1t 2

 0