Balakumar Balachandran, Magrab E.B. Vibrations
Подождите немного. Документ загружается.

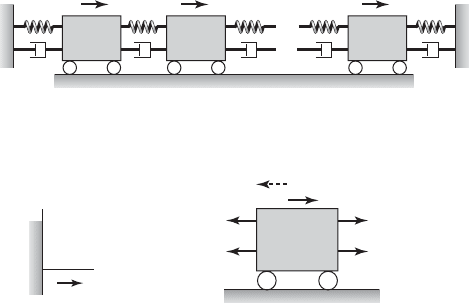
Linear Systems with N Inertial Elements, (N1) Linear Spring Elements,
and (N1) Linear Damper Elements
As a special case of linear multi-degree-of-freedom systems, we consider the
system shown in Figure 7.7. This system is an extension of the two degree-of-
freedom system shown in Figure 7.1. In the figure, m
i
is the mass of the ith in-
ertial element whose motion is described by the generalized coordinate q
i
(t),
which is measured from the point o located on the fixed boundary along the i
direction. The force acting on the ith inertial element is represented by Q
i
(t).
Carrying out a force balance based on the free-body diagram shown in Fig-
ure 7.7b, we obtain the following equation that governs the ith inertial
element:
(7.5a)
Assembling all of the N equations given by Eqs. (7.5a) into matrix form, we
obtain Eq. (7.3) with the circulatory matrix and the gyroscopic ma-
trix and with the following inertia, stiffness, and damping matrices,
respectively,
3M 4 D
m
1
0
p
0
0 m
2
0
o∞o
0
p
m
N
T
3G 4 0
3H 4 0
1c
i
c
i 1
2q
#
i
c
i
q
#
i 1
c
i 1
q
#
i 1
Q
i
1t 2
i 1, 2, . . ., N
m
i
q
$
i
1k
i
k
i1
2q
i
k
i
q
i1
k
i1
q
i1
350 CHAPTER 7 Multiple Degree-of-Freedom Systems
FIGURE 7.7
(a) Linear system with N inertial elements, (N1) spring elements, and (N1) damper ele-
ments and (b) free-body diagram of ith inertial element shown along with the inertial force.
y
k
1
k
2
k
3
k
N 1
k
N
c
1
c
2
c
3
c
N 1
c
N
Q
i
k
i
(q
i
q
i 1
) k
i 1
(q
i
q
i 1
)
c
i
(q
i
q
i 1
) c
i 1
(q
i
q
i 1
)
m
i
q
i
m
i
..
..
..
x
i
o
(a)
(b)
...
q
1
, Q
1
(t) q
2
, Q
2
(t) q
N
, Q
N
(t)
m
1
m
2
m
N

(7.5b)
The inertia matrix given by Eq. (7.5b) is a diagonal matrix, while the
stiffness matrix and the damping matrix given by Eq. (7.5b) are not diagonal
matrices because of the presence of the off-diagonal elements. However, the
stiffness and damping matrices are banded matrices, with each banded matrix
having non-zero elements along three diagonals. All the other elements of
these matrices are zero.
Conservation of Linear Momentum and Angular Momentum
In the absence of external forces—that is,
(7.6a)
—the system linear momentum is conserved. This means that
(7.6b)
Equation (7.6b) is obtained directly by making use of Eq. (1.11) and noting
Eq. (7.6a).
For systems that experience rotational motions, Eq. (1.17) can be used to
examine if a system's angular momentum is conserved. For example, in the
two degree-of-freedom system shown in Figure 7.3, even in the absence of the
external moment—that is, M
o
0—the angular momentum J
o1
J
o2
constant along the k direction. This is to be expected because of the fixed
boundary at the left end.
7.2.3 Lagrange’s Equations of Motion
To use Lagrange’s equations, we start from Eqs. (3.41), where N is the num-
ber of degrees of freedom and the N independent generalized coordinates
used for describing the motion are q
1
, q
2
, . . ., q
N
. Repeating Eqs. (3.41), the
system of N governing equations is given by
(7.7)
d
dt
a
0T
0q
#
j
b
0T
0q
j
0D
0q
#
j
0V
0q
j
Q
j
for j 1, 2, . . . , N
w
#
2
w
#
1
m
1
q
#
1
m
2
q
#
2
p
m
N
q
#
N
constant
Q
1
Q
2
p
Q
N
0
3C 4 F
c
1
c
2
c
2
00
p
0
c
2
c
2
c
3
c
3
0
p
0
0 c
3
o
00 ∞ c
N1
0
oo c
N1
c
N1
c
N
c
N
00
p
0 c
N
c
N
c
N1
V
3K 4 F
k
1
k
2
k
2
00
p
0
k
2
k
2
k
3
k
3
0
p
0
0 k
3
o
00 ∞ k
N1
0
oo k
N1
k
N1
k
N
k
N
00
p
0 k
N
k
N
k
N1
V
7.2 Governing Equations 351

where T is the kinetic energy of the system, V is the potential energy of the
system, D is the Rayleigh dissipation function, and Q
j
is the generalized force
acting on the jth inertial element.
Linear Vibratory Systems
For vibratory systems with linear inertial characteristics, linear stiffness char-
acteristics, and linear viscous damping characteristics, T, V, and D take the
form given by Eqs. (3.43); that is, we have
8
(7.8)
and Q
j
is given by Eq. (3.42). Also,
(7.9a)
It can be shown
9
that the inertia coefficients m
jk
, the stiffness coefficients k
jk
,
and the damping coefficients c
jk
are symmetric; that is,
(7.9b)
In light of Eqs. (7.9b), for a two degree-of-freedom system with linear
characteristics, Eq. (7.8) is written in expanded form as
c
jk
c
kj
k
jk
k
kj
m
jk
m
kj
0
2
D
0q
#
j
0q
#
k
0
2
D
0q
#
k
0q
#
j
0
2
V
0q
j
0q
k
0
2
V
0q
k
0q
j
0
2
T
0q
#
j
0q
#
k
0
2
T
0q
#
k
0q
#
j
D
1
2
5q
#
6
T
3C 45q
#
6
1
2
a
N
j1
a
N
n1
c
jn
q
#
j
q
#
n
V
1
2
5q6
T
3K 45q6
1
2
a
N
j1
a
N
n1
k
jn
q
j
q
n
T
1
2
5q
#
6
T
3M 45q
#
6
1
2
a
N
j1
a
N
n1
m
jn
q
#
j
q
#
n
352 CHAPTER 7 Multiple Degree-of-Freedom Systems
8
The quadratic forms shown for T, V, and D in Eqs. (7.8) are strictly valid for systems with lin-
ear characteristics. However, the kinetic energy T is not always a function of only velocities as
shown here. Systems in which the kinetic energy has the quadratic form shown in Eqs. (7.8) are
called natural systems. As discussed later in this chapter, for systems such as that given in Ex-
ample 7.4, where rotation effects are present, the form of the kinetic energy T is different from
that shown in Eqs. (7.8). As noted in Chapter 2, gravity forces can also contribute to the poten-
tial energy of the system. For a general system with holonomic constraints, Eqs. (7.7) will be used
directly in this book to obtain the governing equations.
9
L. Meirovitch, Elements of Vibration Analysis, 2nd ed., McGraw Hill, NY, pp. 260–261 (1986).

(7.10)
On substituting Eqs. (7.10) into Eqs. (7.7) and performing the indicated op-
erations, we obtain the following system of two coupled ordinary differential
equations
(7.11)
which are written in the matrix form
(7.12)
where the square matrix is the inertia matrix, the square matrix is the
stiffness matrix, and square matrix is the damping matrix. They are given
by, respectively,
(7.13)
The displacement vector {q}, the velocity vector { }, the acceleration vector
{ }, and the vector of generalized forces {Q} are given by the column vectors
(7.14)
Illustration of Derivation of Governing Equations for a
Two Degree-of-Freedom System
Consider again the two degree-of-freedom system shown in Figure 7.1, with
linear springs and linear dampers. The kinetic energy and potential energy are
given by
(7.15)
1
2
1k
1
k
2
2x
1
2
k
2
x
1
x
2
1
2
1k
2
k
3
2x
2
2
V
1
2
k
1
x
1
2
1
2
k
2
1x
1
x
2
2
2
1
2
k
3
x
2
2
T
1
2
m
1
x
#
1
2
1
2
m
2
x
#
2
2
5q
$
6 e
q
$
1
q
$
2
f,
5q
#
6 e
q
#
1
q
#
2
f,
5q6 e
q
1
q
2
f,
and
5Q6 e
Q
1
Q
2
f
q
$
q
#
3M 4 c
m
11
m
12
m
12
m
22
d,
3K 4 c
k
11
k
12
k
12
k
22
d,
and
3C 4 c
c
11
c
12
c
12
c
22
d
3C4
3K 43M 4
3M 45q
$
6 3C45q
#
6 3K45q6 5Q6
m
12
q
$
1
m
22
q
$
2
c
12
q
#
1
c
22
q
#
2
k
12
q
1
k
22
q
2
Q
2
m
11
q
$
1
m
12
q
$
2
c
11
q
#
1
c
12
q
#
2
k
11
q
1
k
12
q
2
Q
1
D
1
2
a
2
j1
a
2
n1
c
jn
q
#
j
q
#
n
1
2
c
11
q
#
1
2
c
12
q
#
1
q
#
2
1
2
c
22
q
#
2
2
V
1
2
a
2
j1
a
2
n1
k
jn
q
j
q
n
1
2
k
11
q
1
2
k
12
q
1
q
2
1
2
k
22
q
2
2
T
1
2
a
2
j1
a
2
n1
m
jn
q
#
j
q
#
n
1
2
m
11
q
#
1
2
m
12
q
#
1
q
#
2
1
2
m
22
q
#
2
2
7.2 Governing Equations 353

the dissipation function D takes the form
(7.16)
and Q
1
f
1
and Q
2
f
2
.
Comparing Eqs. (7.15) and (7.16) with Eqs. (7.10), the corresponding
inertia coefficients m
jk
, stiffness coefficients k
jk
, and damping coefficients c
jk
are identified. Upon using Eqs. (7.4a), this leads to the governing system
(7.17)
where the different square matrices are
(7.18)
and the different column vectors are
(7.19)
In certain situations, it is necessary to use Eqs. (7.7) directly. To illustrate this
procedure, we evaluate the following derivatives based on Eqs. (7.15) and (7.16):
(7.20)
On substituting Eqs. (7.20) into Eqs. (7.7); that is,
(7.21a)
d
dt
a
0T
0x
#
2
b
0T
0x
2
0D
0x
#
2
0V
0x
2
Q
2
d
dt
a
0T
0x
#
1
b
0T
0x
1
0D
0x
#
1
0V
0x
1
Q
1
0D
0x
#
2
c
2
1x
#
1
x
#
2
2 c
3
x
#
2
1c
2
c
3
2x
#
2
c
2
x
#
1
0D
0x
#
1
c
1
x
#
1
c
2
1x
#
1
x
#
2
2 1c
1
c
2
2x
#
1
c
2
x
#
2
0V
0x
2
k
2
1x
1
x
2
2 k
3
x
2
1k
2
k
3
2x
2
k
2
x
1
0V
0x
1
k
1
x
1
k
2
1x
1
x
2
2 1k
1
k
2
2x
1
k
2
x
2
0T
0x
1
0,
0T
0x
2
0
d
dt
a
0T
0x
#
1
b m
1
x
$
1
,
d
dt
a
0T
0x
#
2
b m
2
x
$
2
5x
$
6 e
x
$
1
x
2
$
f,
5x
#
6 e
x
#
1
x
#
2
f,
5x6 e
x
1
x
2
f,
and
5F6 e
f
1
f
2
f
3C 4 c
c
1
c
2
c
2
c
2
c
2
c
3
d
3M 4 c
m
1
0
0 m
2
d,
3K 4 c
k
1
k
2
k
2
k
2
k
2
k
3
d,
and
3M 45x
$
6 3C45x
#
6 3K45x6 5F 6
1
2
1c
1
c
2
2x
#
1
2
c
2
x
#
1
x
#
2
1
2
1c
2
c
3
2x
#
2
2
D
1
2
c
1
x
#
1
2
1
2
c
2
1x
#
1
x
#
2
2
2
1
2
c
3
x
#
2
2
354 CHAPTER 7 Multiple Degree-of-Freedom Systems
we obtain
(7.21b)
which yields the same matrix form as Eqs. (7.1b).
In light of Eqs. (7.9a) and (7.9b), the equations of motion obtained by us-
ing Lagrange’s equations for linear systems always have symmetric inertia
and stiffness matrices. For systems in which the dissipation is modeled by
the Rayleigh dissipation function, the damping matrix is also symmetric.
These symmetry properties are not necessarily explicit when the governing
equations are obtained by using force-balance and moment-balance methods.
However, the form of the governing equations obtained by using force-
balance and moment-balance methods can be manipulated to obtain the same
form as that obtained through Lagrange’s equations.
Next, different examples are provided to illustrate the use of Lagrange’s
equations for deriving the equations of motion of multi-degree-of-freedom
systems. When using Lagrange’s equations, in cases where the expressions
for kinetic energy, potential energy, and dissipation function are in the form
of Eqs. (7.8), these equations are directly used to identify the coefficients in
the inertia, stiffness, and damping matrices in the governing equations.
EXAMPLE 7.5
System with a translating mass attached to an oscillating disk
Consider the system shown in Figure 7.8 with linear springs and linear
dampers and a rotating element. A massless rigid bar connects the rotating el-
ement to the base of the combination of the spring k
2
and the damper c
2
. The
inertial element m
1
is treated as a translating point mass and the other inertial
element is treated as a rigid body rotating about the point o. The position x of
mass m
1
is the displacement measured from the fixed end and the other gen-
eralized coordinate u is the angular position of the disk measured from the
vertical. We shall use Lagrange’s equations to determine the governing equa-
tions of motion of the system.
m
2
x
$
2
1c
2
c
3
2x
#
2
c
2
x
#
1
1k
2
k
3
2x
2
k
2
x
1
f
2
1t 2
m
1
x
$
1
1c
1
c
2
2x
#
1
c
2
x
#
2
1k
1
k
2
2x
1
k
2
x
2
f
1
1t 2
7.2 Governing Equations 355
FIGURE 7.8
Translating and rotating system with two degrees of freedom.
k
2
c
2
m
2
, J
o
x, f(t)
k
1
c
1
m
1
i
x
y
z
j
k
o
r
A
, M
o
(t)
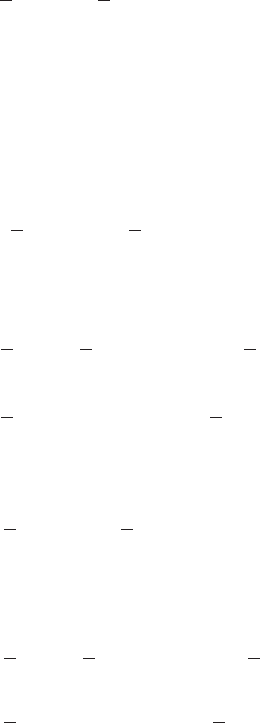
The kinetic energy of the system is given by
(a)
We assume that the mass center of the disk coincides with the point o and that
the angular oscillations in u are “small.” The “small” angle assumption allows
us to express the horizontal translation of point A as being equal to ru. The
potential energy is then given by
(b)
The dissipation function takes the form
(c)
Since Eqs. (a) through (c) are in the standard form of Eqs. (7.8), we identify
the inertial, stiffness, and damping coefficients by comparing Eqs. (a)
through (c) to Eqs. (7.10) and associating x with q
1
and u with q
2
. In addi-
tion, we make use of Eq. (3.42) to recognize the generalized forces as Q
1
f(t) and Q
2
M
o
(t). Then, the governing equations become
(d)
Since the damping and stiffness matrices have non-zero off-diagonal terms,
Eqs. (d) are coupled.
c
m 0
0 J
o
de
x
$
u
$
f e
c
1
c
2
rc
2
rc
2
r
2
c
2
fe
x
#
u
#
f e
k
1
k
2
rk
2
rk
2
r
2
k
2
fe
x
u
f e
f 1t 2
M
o
1t 2
f
1
2
1c
1
c
2
2x
#
2
c
2
ru
#
x
#
1
2
c
2
r
2
u
#
2
1
2
c
1
x
#
2
1
2
c
2
r
2
u
#
2
c
2
ru
#
x
#
1
2
c
2
x
#
2
Dissipation
associated with
damper c
2
Dissipation
associated with
damper c
1
D
1
2
c
1
x
#
2
1
2
c
2
1x
#
ru
#
2
2
1
2
1k
1
k
2
2x
2
k
2
rux
1
2
k
2
r
2
u
2
1
2
k
1
x
2
1
2
k
2
r
2
u
2
k
2
rux
1
2
k
2
x
2
Potential energy
associated with
spring k
2
Potential energy
associated with
spring k
1
V
1
2
k
1
x
2
1
2
k
2
1x ru 2
2
Kinetic energy of
rigid body J
o
Kinetic energy
of mass m
1
T
1
2
m
1
x
#
2
1
2
J
o
u
#
2
356 CHAPTER 7 Multiple Degree-of-Freedom Systems
⎫
⎬
⎭
⎫
⎬
⎭
⎫
⎬
⎭
⎫
⎬
⎭
⎫
⎪
⎬
⎪
⎭
⎫
⎪
⎬
⎪
⎭

EXAMPLE 7.6 System with bounce and pitch motions revisited
Consider the rigid bar shown in Figure 7.5a. The generalized coordinates are
y and u, which are located at the center of gravity of the beam. We shall use
Lagrange’s equations to obtain the governing equations of motion of this two
degree-of-freedom system.
For a rigid bar undergoing planar motions, we use Eq. (1.24) to find that
the kinetic energy is given by
(a)
Taking into account the potential energy due to the spring displacement and
the work done by the gravity loading, the potential energy is
(b)
The dissipation function is of the form
(c)
Since Eqs. (b) and (c) are not in the standard form of Eqs. (7.8), the equa-
tions of motion are obtained directly by using Eqs. (7.7). Thus, recognizing
that q
1
y, the first equation of Eqs. (7.7) takes the form
(d)
d
dt
a
0T
0y
#
b
0T
0y
0D
0y
#
0V
0y
Q
y
1
2
1c
1
L
1
2
c
2
L
2
2
2u
#
2
cos
2
u
1
2
1c
1
c
2
2y
#
2
1c
1
L
1
c
2
L
2
2u
#
y
#
cos u
Dissipation associated
with damper c
2
Dissipation associated
with damper c
1
D
1
2
c
1
1y
#
L
1
u
#
cos u2
2
1
2
c
2
1y
#
L
2
u
#
cos u2
2
1
2
1k
1
L
1
2
k
2
L
2
2
2sin
2
u mgy
1
2
1k
1
k
2
2y
2
1k
1
L
1
k
2
L
2
2y sin u
Potential energy
associated with
gravity loading
Potential energy associated
with spring k
2
Potential energy associated
with spring k
1
V
1
2
k
1
1y L
1
sin u2
2
1
2
k
2
1y L
2
sin u2
2
mgy
Kinetic energy
associated with
rotation about
center of mass
Kinetic energy
associated with
translation of center
of mass m
T
1
2
my
#
2
1
2
J
G
u
#
2
7.2 Governing Equations 357
⎫
⎪
⎪
⎬
⎪
⎪
⎭
⎫
⎪
⎪
⎬
⎪
⎪
⎭
⎫
⎪
⎪
⎬
⎪
⎪
⎭
⎫
⎪
⎪
⎬
⎪
⎪
⎭
⎫
⎬
⎭
⎫
⎬
⎭
⎫
⎬
⎭

Noting that Q
y
0, we obtain from Eqs. (a) through (d) that the first equation
of motion is
(e)
Recognizing that q
2
u, the second equation of Eqs. (7.7) assumes
the form
(f)
Recognizing that Q
u
0, we arrive from Eqs. (a), (b), (c), and (f ) at the sec-
ond equation of motion
(g)
Equations (e) and (g) are identical to Eqs. (a) and (b) of Example 7.3, which
were obtained by using force-balance and moment-balance methods.
EXAMPLE 7.7
Pendulum absorber
Consider the two degree-of-freedom system shown in Figure 7.9, in which
the generalized coordinate x is used to locate the mass m
1
and the other gener-
alized coordinate u is used to specify the angular position of the pendulum.
This type of system can model a pendulum absorber,
10
which is used in many
1k
1
L
1
k
2
L
2
2y cos u 1k
1
L
1
2
k
2
L
2
2
2sin u cos u 0
J
G
u
$
1c
1
L
1
c
2
L
2
2y
#
cos u 1c
1
L
1
2
c
2
L
2
2
2u
#
cos
2
u
d
dt
a
0T
0u
#
b
0T
0u
0D
0u
#
0V
0u
Q
u
1k
1
L
1
k
2
L
2
2sin u mg
my
$
1c
1
c
2
2y
#
1c
1
L
1
c
2
L
2
2u
#
cos u 1k
1
k
2
2y
358 CHAPTER 7 Multiple Degree-of-Freedom Systems
10
J. J. Hollkamp, R. L. Bagley, and R. W. Gordon, “A Centrifugal Pendulum Absorber for Rotat-
ing, Hollow Engine Blades,” J. Sound Vibration, Vol. 219, No. 3, pp. 539–549 (1999); Z.-M. Ge
and T.-N. Lin, “Regular and Chaotic Dynamic Analysis and Control of Chaos of an Elliptical
Pendulum on a Vibrating Basement,” J. Sound Vibration, Vol. 230, No. 5, pp. 1045–1068 (2000);
and A. Ertas et al., “Performance of Pendulum Absorber for a Nonlinear System of Varying Ori-
entation,” J. Sound Vibration, Vol. 229, No. 4, pp. 913–933 (2000).
FIGURE 7.9
Pendulum absorber.
f(t)
i
x
x
k
L
y
z
o
j
k
m
1
m
2

applications. The mass of the rod of length L is assumed to be negligible. In this
example, we obtain the nonlinear equations of motion and then linearize the
governing nonlinear equations about an equilibrium position of the system.
Governing Equations
We see from Figure 7.9 that the position of mass m
2
is
Therefore, the velocity of mass m
2
is given by
(a)
Making use of Eq. (1.22) and Eq. (a), the kinetic energy for the system is
(b)
The potential energy of the system is
(c)
where the datum has been chosen at the bottom position of the pendulum.
Since Eqs. (b) and (c) are not in the form of Eqs. (7.8), we use Eqs. (7.7) di-
rectly to obtain the equations of motion. On using Eqs. (7.7) with q
1
x,
q
2
u, and recognizing that the generalized forces are Q
1
f(t) and Q
2
0
and D 0, Eqs. (7.7) becomes
(d)
Upon substituting Eqs. (b) and (c) into Eq. (d), we obtain
(e)m
2
L
2
u
$
m
2
Lx
$
cos u m
2
gL sin u 0
1m
1
m
2
2x
$
m
2
Lu
$
cos u m
2
Lu
#
2
sin u kx f 1t2
d
dt
a
0T
0u
#
b
0T
0u
0V
0u
0
d
dt
a
0T
0x
#
b
0T
0x
0V
0x
f 1t 2
Potential energy
associated with
gravity loading
Potential energy
associated with
spring k
V
1
2
kx
2
m
2
gL11 cos u 2
1
2
1m
1
m
2
2x
#
2
m
2
L cos ux
#
u
#
1
2
m
2
L
2
u
#
2
1
2
m
1
x
#
2
1
2
m
2
31x
#
Lu
#
cos u2
2
1Lu
#
sin u2
2
4
Kinetic energy of
pendulum of mass m
2
Kinetic energy
of mass m
1
T
1
2
m
1
x
#
2
1
2
m
2
1V
m
#
V
m
2
V
m
dr
m
dt
1x
#
Lu
#
cos u2i Lu
#
sin uj
r
m
1x L sin u 2i L cos uj
7.2 Governing Equations 359
⎫
⎪
⎬
⎪
⎭
⎫
⎬
⎭
⎫
⎪
⎪
⎬
⎪
⎪
⎭
⎫
⎬
⎭
