Balakumar Balachandran, Magrab E.B. Vibrations
Подождите немного. Документ загружается.


Static-Equilibrium Positions
Setting the accelerations and velocities and the time-dependent forcing f(t) to
zero in Eqs. (e), the equations governing the equilibrium positions x
o
and u
o
of the system are
(f)
From Eqs. (f), the equilibrium positions of the system are obtained as
(g)
where the first of Eqs. (g) corresponds to the bottom position of the pendu-
lum and the second of Eqs. (g) corresponds to the pendulum being rotated
by 180°.
Linearization
Considering “small” oscillations about the equilibrium position (0,0) and lin-
earizing the equations of motion given by Eqs. (e) along the lines of what was
illustrated with the use of Eqs. (g) of Example 7.3, we obtain
(h)
which in matrix form reads as
(i)
In Eq. (i), the gravity loading appears explicitly in the equations governing
“small” oscillations about the static-equilibrium position. In this case, the
governing equations are coupled due to the non-zero off-diagonal terms in the
inertia matrix.
EXAMPLE 7.8
Bell and clapper
11
Consider the bell and clapper shown in Figure 7.10. We shall derive the gov-
erning equations of motion for this system by assuming that the bell and clap-
per do not come into contact. From the figure, it is seen that the bell rotates
about the fixed point O
1
and the clapper rotates about the point O
2
that moves
with the bell. The bell has a rotational inertia of J
1
about its centroid, and the
clapper has a rotational inertia J
2
about its centroid. The locations of the cen-
troids b
1
of the bell and b
2
of the clapper from O
1
are given by the positions
r
1
and r
2
, respectively, as
c
m
1
m
2
m
2
L
m
2
Lm
2
L
2
de
x
$
u
$
f c
k 0
0 m
2
gL
de
x
u
f e
f 1t 2
0
f
m
2
L
2
u
$
m
2
Lx
$
m
2
gLu 0
1m
1
m
2
2x
$
m
2
Lu
$
kx f 1t 2
1x
o
, u
o
2 10, 0 2
and
1x
o
, u
o
2 10, p 2
m
2
gL sin u
o
0
kx
o
0
360 CHAPTER 7 Multiple Degree-of-Freedom Systems
11
H. M. Hansen and P. F. Chenea, Mechanics of Vibrations, John Wiley & Sons, New York,
pp. 133–137, 1953.

(a)
The corresponding velocities are
(b)
The kinetic energy of the system is
(c)
The potential energy of the system with respect to the datum at point O
1
is
(d)
If we assume that there is viscous damping at O
1
and O
2
, then the dissipation
function is
(e)
where c
t1
and c
t2
are the torsion damping coefficients for the bell and clapper
motions, respectively.
If we choose the generalized coordinates q
1
u
1
and q
2
u
2
, assume that
Q
1
M
1
(t) and Q
2
M
2
(t) 0, the Lagrange equations become
(f)
Upon substituting Eqs. (c), (d), and (e) into Eq. (f) and performing the indi-
cated operations, we obtain
(g)
c
t2
u
#
1
c
t2
u
#
2
m
2
gd
2
sin u
2
0
1m
2
d
2
2
J
2
2u
$
2
m
2
ad
2
u
$
1
cos1u
1
u
2
2 m
2
ad
2
u
#
2
1
sin1u
1
u
2
2
1c
t1
c
t2
2u
#
1
c
t2
u
#
2
1m
1
d
1
m
2
a2g sin u
1
M
1
1t 2
1m
1
d
2
1
J
1
m
2
a
2
2u
$
1
m
2
ad
2
u
$
2
cos1u
1
u
2
2 m
2
ad
2
u
#
2
2
sin1u
1
u
2
2
d
dt
a
0T
0u
#
2
b
0T
0u
2
0D
0u
#
2
0V
0u
2
0
d
dt
a
0T
0u
#
1
b
0T
0u
1
0D
0u
#
1
0V
0u
1
M
1
1t 2
D
1
2
c
t1
u
#
2
1
1
2
c
t2
1u
#
1
u
#
2
2
2
V m
1
gd
1
cos u
1
m
2
g1d
2
cos u
2
a cos u
1
2
1
2
1m
1
d
2
1
J
1
m
2
a
2
2u
#
2
1
1
2
1m
2
d
2
2
J
2
2u
#
2
2
m
2
ad
2
u
#
1
u
#
2
cos1u
1
u
2
2
1
2
m
2
11au
#
1
cos u
1
d
2
u
#
2
cos u
2
2
2
1au
#
1
sin u
1
d
2
u
#
2
sin u
2
2
2
2
1
2
m
1
11d
1
u
#
1
cos u
1
2
2
1d
1
u
#
1
sin u
1
2
2
2
1
2
J
1
u
#
2
1
1
2
J
2
u
#
2
2
T
1
2
m
1
1v
1
#
v
1
2
1
2
m
2
1v
2
#
v
2
2
1
2
J
1
u
#
2
1
1
2
J
2
u
#
2
2
v
2
1au
#
1
cos u
1
d
2
u
#
2
cos u
2
2i 1au
#
1
sin u
1
d
2
u
#
2
sin u
2
2j
v
1
d
1
u
#
1
cos u
1
i d
1
u
#
1
sin u
1
j
r
2
1a sin u
1
d
2
sin u
2
2i 1a cos u
1
d
2
cos u
2
2j
r
1
d
1
sin u
1
i d
1
cos u
1
j
7.2 Governing Equations 361
b
1
b
2
m
1
d
2
d
1
2
1
a
x
y
O
2
O
1
i
j
Bell
m
2
FIGURE 7.10
Bell and clapper.
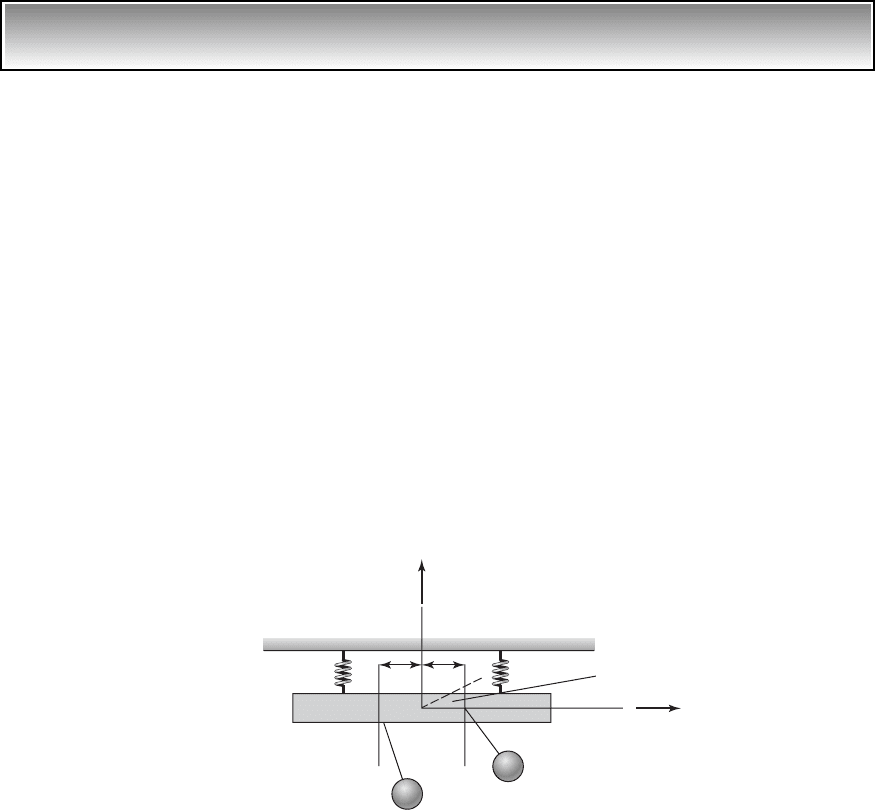
To obtain the equations governing “small” oscillations about the equilib-
rium position u
j
0, we assume that sin u
j
u
j
and cos u
j
1. Then Eqs. (g)
lead to the following coupled linear equations
(h)
EXAMPLE 7.9
Three coupled nonlinear oscillators—Lavrov’s device
12
We shall derive the governing equations of the device shown in Figure 7.11.
This device consists of a rigid bar of mass m
o
that is supported on soft springs
k that can translate in the xy plane and rotate about its center of mass with an-
gular displacement w. The rotary inertia of the bar about its center of mass is
J. Two pendulums, which are of different lengths L
1
and L
2
and the same mass
m, are attached to the bar a distance a on either side of the bar’s center of
mass. The positions of the pendulums are given by
(a)
where r
1
is the position vector from point O to the mass of the pendulum of
length L
1
and r
2
is the position vector from point O to the mass of the pendu-
lum of length L
2
. Hence, the velocity of each mass is
(b)
The system kinetic energy is
v
2
1x
#
L
2
w
#
2
cosw
2
aw
#
sinw 2i 1y
#
L
2
w
#
2
sinw
2
aw
#
cosw 2j
v
1
1x
#
L
1
w
#
1
cosw
1
aw
#
sin w2i 1y
#
L
1
w
#
1
sin w
1
aw
#
cosw 2j
r
2
1x L
2
sin w
2
a cos w2i 1y L
2
cos w
2
a sin w2j
r
1
1x L
1
sin w
1
a cos w2i 1y L
1
cos w
1
a sin w2j
m
2
ad
2
u
$
1
1m
2
d
2
2
J
2
2u
$
2
c
t2
u
#
1
c
t2
u
#
2
m
2
gd
2
u
2
0
1m
1
d
2
1
J
1
m
2
a
2
2u
$
1
m
2
ad
2
u
$
2
1c
t1
c
t2
2u
#
1
c
t2
u
#
2
1m
1
d
1
m
2
a2gu
1
M
1
1t 2
362 CHAPTER 7 Multiple Degree-of-Freedom Systems
12
P. S. Landa, Regular and Chaotic Oscillations, Springer, Berlin, pp. 67–71, 2001. The case
where the mass doesn’t rotate and there are N pendulums has been studied by A. Vyas and A. K.
Bajaj, “Dynamics of Autoparametric Vibration Absorbers Using Multiple Pendulums”, J. Sound
Vibration, 246 (1), pp. 115–135, 2001.
FIGURE 7.11
Lavrov's device.
m
o
, J
k
k
aa
1
2
x
y
L
1
L
2
O
i
j
m
m

(c)
where
The system potential energy is
(d)
The Lagrange equations, Eqs. (7.7), for this undamped and unforced system
become
(e)
since D 0. Upon substituting Eqs. (c) and (d) into Eqs. (e) and performing
the indicated operations, we obtain
(f)
mL
2
2
w
$
2
mL
2
1x
$
cos w
2
y
$
sin w
2
2 maL
2
1w
$
sin1w w
2
2 w
#
2
cos1w w
2
22 mgL
2
sin w
2
0
mL
2
1
w
$
1
mL
1
1x
$
cos w
1
y
$
sin w
1
2 maL
1
1w
$
sin1w w
1
2 w
#
2
cos1w w
1
22 mgL
1
sin w
1
0
maL
2
1w
$
2
sin1w w
2
2 w
#
2
2
cos1w w
2
22 0
J
T
w
$
maL
1
1w
$
1
sin1w w
1
2 w
#
2
1
cos 1w w
1
22 2a
2
k sin w cos w
m
T
y
$
mL
1
1w
$
1
sin w
1
w
#
2
1
cos w
1
2 mL
2
1w
$
2
sin w
2
w
#
2
2
cos w
2
2 2ky m
T
g 0
m
T
x
$
mL
1
1w
$
1
cos w
1
w
#
2
1
sin w
1
2 mL
2
1w
$
2
cos w
2
w
#
2
2
sin w
2
2 0
d
dt
a
0T
0w
#
2
b
0T
0w
2
0V
0w
2
Q
w
2
0
d
dt
a
0T
0w
#
1
b
0T
0w
1
0V
0w
1
Q
w
1
0
d
dt
a
0T
0w
#
b
0T
0w
0V
0w
Q
w
0
d
dt
a
0T
0y
#
b
0T
0y
0V
0y
Q
y
0
d
dt
a
0T
0x
#
b
0T
0x
0V
0x
Q
x
0
V mgL
1
cos w
1
mgL
2
cos w
2
1
2
k 1y a sin w2
2
1
2
k 1y a sin w2
2
m
T
gy
J
T
J 2ma
2
m
T
m
o
2m
maw
#
1L
1
w
#
1
sin1w w
1
2 L
2
w
#
2
sin1w w
2
22
mx
#
1L
1
w
#
1
cos w
1
L
2
w
#
2
cos w
2
2 my
#
1L
1
w
#
1
sin w
1
L
2
w
#
2
sin w
2
2
1
2
m
T
1x
#
2
y
#
2
2
1
2
J
T
w
#
2
1
2
m 1L
2
1
w
#
2
1
L
2
2
w
#
2
2
2
1
2
m B1x
#
L
2
w
#
2
cos w
2
aw
#
sin w2
2
1y
#
L
2
w
#
2
sin w
2
aw
#
cos w2
2
R
1
2
m B1x
#
L
1
w
#
1
cos w
1
aw
#
sin w2
2
1y
#
L
1
w
#
1
sin w
1
aw
#
cos w2
2
R
1
2
m
o
1x
#
2
y
#
2
2
1
2
Jw
#
2
T
1
2
m
o
x
#
2
1
2
m
o
y
#
2
1
2
Jw
#
2
1
2
m1v
1
#
v
1
2
1
2
m1v
2
#
v
2
2
7.2 Governing Equations 363

When m 0, we have the case of bounce and pitch motions discussed in
Example 7.3, except that we have removed the restriction that the center of
mass of the bar must only move in the vertical direction.
EXAMPLE 7.10
Governing equations of a rate gyroscope
We revisit the gyro-sensor presented in Example 7.4 and obtain the equations
of motion by using Lagrange’s equations. Therefore, we construct the kinetic
energy T, as follows. From Eq. (b) of Example 1.3, we have that
where e
1
and e
2
are the unit vectors fixed in the rotating plane. Therefore, the
kinetic energy is
(a)
The potential energy V and dissipation function D are, respectively,
(b)
Because of the rotation v
z
, the kinetic energy is not in the standard form
shown in Eq. (7.8) and we have an example of a nonnatural system.
13
Upon using Eqs. (a), Eqs. (b), and Eqs. (7.7), and recognizing that the gen-
eralized coordinates are q
1
x and q
1
y and that the associated generalized
forces are
(c)
we carry out the indicated operations in Eqs. (7.7) to obtain equations that are
identical to those given by Eqs. (c) and (d) in Example 7.4.
EXAMPLE 7.11
Governing equations of hand-arm vibrations
14
In Chapter 3, we considered the development of the governing equation of
motion of a hand-arm system modeled as a rigid body with one degree of free-
dom. In this example, a multi-degree-of-freedom system model is used to
Q
1
f
x
and
Q
2
0
D
1
2
c
x
x
#
2
1
2
c
y
y
#
2
V
1
2
k
x
x
2
1
2
k
y
y
2
1
2
m1x
#
2
y
#
2
2 mv
z
1yx
#
xy
#
2
1
2
mv
2
z
1y
2
x
2
2
T
1
2
m1v
#
v2
1
2
m1x
#
v
z
y2
2
1
2
m1y
#
v
z
x2
2
v 1x
#
v
z
y2e
1
1y
#
v
z
x2e
2
364 CHAPTER 7 Multiple Degree-of-Freedom Systems
13
L. Meirovitch, ibid.
14
C. Thomas, S. Rakheja, R. B. Bhat, and I. Stiharu, “A Study of the Modal Behavior of the Hu-
man Hand-Arm System,” J. Sound Vibration, Vol. 191, No. 1, pp. 171–176 (1996).
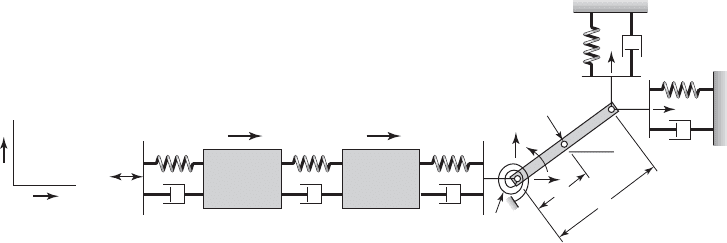
study hand-arm vibrations. The model shown in Figure 7.12 has five degrees
of freedom and the associated generalized coordinates are x
1
, x
2
, x
3
, y
3
, and u
3
.
The angle shows the nominal position of the system about which we wish
to study the vibrations of the system. It is assumed that 0 throughout this
discussion. The coordinates x
1
, x
2
, and x
3
describe the longitudinal motions of
the hand, the forearm, and the elbow, respectively. The coordinate y
3
de-
scribes the vertical motion of the elbow and the coordinate u
3
describes the ro-
tation of the elbow joint about the nominal position. In Figure 7.12, x
o
repre-
sents the external disturbance acting on the hand.
The hand is treated as a point mass of mass m
1
, the forearm is treated as
a point mass of mass m
2
, and the upper arm is treated as a rigid body of mass
m
3
and rotary inertia J
3g
. In addition, translation springs with stiffness of k
1
through k
5
and a torsion spring of stiffness k
t3
are used to represent the flexi-
bility of the various members. Similarly, translation dampers with damping
coefficients of c
1
through c
5
and a torsion damper with damping coefficient c
t3
are also used.
To construct the different quantities, we first note that the position vector
of the center of mass of the rigid mass m
3
from the origin o is given by
(a)
and, therefore, the velocity of the center of mass is
(b)
In addition, the displacements x
4
and y
4
are related to x
3
, y
3
, and u
3
as
follows:
(c)y
4
y
3
Lsin 1u
~
u
3
2
x
4
x
3
Lcos 1u
~
u
3
2
V
g
1x
#
3
L
g
u
#
3
sin1u
~
u
3
22i 1y
#
3
L
g
u
#
3
cos1u
~
u
3
22j
r
g
1x
3
L
g
cos 1u
~
u
3
22i 1y
3
L
g
sin 1u
~
u
3
22j
u
~
#
u
~
7.2 Governing Equations 365
FIGURE 7.12
A five degree-of-freedom model used to study planar vibrations of the human hand-arm system. The nominal position of the upper
arm is specified by . Source: Reprinted by permission of Federation of European Biochemical Societies from Journal of Sound Vibra-
tion, 191, C. Thomas, S. Rakheja, R. B. Bhat, and I. Stiharu, FEBS Letters, “A Study of the Model Behaviour of the Human Hand-Arm
System,” pp. 171–176, Copyright © 1996, with permission from Elsevier Science.
u
~
L
g
k
1
x
1
c
1
k
4
k
5
x
4
x
3
y
3
3
y
4
c
4
c
5
k
2
c
2
k
3
c
3
m
1
x
2
m
2
i
x
o
y
j
L
~
k
t3
, c
t3
x
o
m
3
, J
3g
Then, making use of Eq. (1.22) and Eqs. (a) through (c), the kinetic energy of
the system is
(d)
and the potential energy of the system is given by
(e)
The dissipation function D is given by
(f)
From the form of Eqs. (d) through (f), it is clear that we need to make use
of Eqs. (7.7) directly to obtain the governing equations of motion. In terms of
the chosen coordinates for this five degree-of-freedom system, we have
d
dt
a
0T
0x
#
3
b
0T
0x
3
0D
0x
#
3
0V
0x
3
Q
3
d
dt
a
0T
0x
#
2
b
0T
0x
2
0D
0x
#
2
0V
0x
2
Q
2
d
dt
a
0T
0x
#
1
b
0T
0x
1
0D
0x
#
1
0V
0x
1
Q
1
Dissipation associated with damper c
5
Dissipation associated with damper c
4
1
2
c
4
1x
#
3
Lu
#
3
sin 1u
~
u
3
22
2
1
2
c
5
1y
#
3
Lu
#
3
cos 1u
~
u
3
22
2
Dissipation
associated with
damper c
t3
Dissipation associated
with damper c
3
Dissipation associated
with damper c
2
Dissipation associated
with damper c
1
D
1
2
c
1
1x
#
1
x
#
o
2
2
1
2
c
2
1x
#
2
x
#
1
2
2
1
2
c
3
1x
#
3
x
#
2
2
2
1
2
c
t3
u
#
3
2
Potential energy associated with gravity loading
m
3
g1y
3
L
g
sin 1u
~
u
3
22
Potential energy associated with spring k
5
Potential energy associated with spring k
4
1
2
k
4
1x
3
Lcos 1u
~
u
3
22
2
1
2
k
5
1y
3
Lsin 1u
~
u
3
22
2
Potential energy
associated with spring k
t3
Potential energy
associated with spring k
3
Potential energy
associated with spring k
2
Potential energy
associated with spring k
1
V
1
2
k
1
1x
1
x
o
2
2
1
2
k
2
1x
2
x
1
2
2
1
2
k
3
1x
3
x
2
2
2
1
2
k
t3
1u
~
u
3
2
2
1y
#
3
L
g
u
#
3
cos1u
~
u
3
22
2
R
1
2
J
3g
u
#
3
2
1
2
m
1
x
#
1
2
1
2
m
2
x
#
2
2
1
2
m
3
B1x
#
3
L
g
u
#
3
sin 1u
~
u
3
22
2
Kinetic energy of the upper arm
Kinetic energy
of the forearm
Kinetic energy
of the hand
T
1
2
m
1
x
#
1
2
1
2
m
2
x
#
2
2
1
2
m
3
1V
g
#
V
g
2
1
2
J
3g
u
#
3
2
366 CHAPTER 7 Multiple Degree-of-Freedom Systems
⎫
⎬
⎭
⎫
⎬
⎭
⎫
⎪
⎪
⎪
⎬
⎪
⎪
⎪
⎭
⎫
⎪
⎬
⎪
⎭
⎫
⎪
⎬
⎪
⎭
⎫
⎪
⎬
⎪
⎭
⎫
⎪
⎬
⎪
⎭
⎫
⎪
⎪
⎪
⎬
⎪
⎪
⎪
⎭
⎫
⎪
⎪
⎪
⎬
⎪
⎪
⎪
⎭
⎫
⎪
⎪
⎪
⎬
⎪
⎪
⎪
⎭
⎫
⎪
⎪
⎪
⎪
⎬
⎪
⎪
⎪
⎪
⎭
⎫
⎪
⎪
⎪
⎪
⎬
⎪
⎪
⎪
⎪
⎭
⎫
⎪
⎬
⎪
⎭
⎫
⎪
⎬
⎪
⎭
⎫
⎪
⎬
⎪
⎭
⎫
⎬
⎭

(g)
where the generalized forces are given by
(h)
since the external disturbance acting on the hand has already been taken into
account in determining the kinetic energy, the potential energy, and the dissi-
pation function. In addition, gravity loading has been accounted for in the sys-
tem potential energy. After substituting Eqs. (d) through (f) and Eq. (h) into
Eq. (g) and carrying out the different differentiations in Eqs. (g), we arrive at
the following governing equations of motion of the hand-arm system:
(i)
Linearization
We now linearize the nonlinear system of equations given by Eqs. (i) about
the nominal position to describe “small” oscillations about this position. To
this end, we use Eqs. (g) of Example 7.3 to determine that
(j)
Making use of Eqs. (j) in Eqs. (i) and retaining only linear terms, we obtain
the following system of linear equations:
1c
3
c
4
2x
#
3
c
3
x
#
2
c
4
Lu
#
3
sin u
~
k
4
L cos u
~
m
3
3x
$
3
L
g
u
$
3
sin u
~
4 1k
3
k
4
2x
3
k
3
x
2
k
4
Lu
3
sin u
~
m
2
x
$
2
1k
2
k
3
2x
2
k
2
x
1
k
3
x
3
1c
2
c
3
2x
#
2
c
2
x
#
1
c
3
x
#
3
0
m
1
x
$
1
1k
1
k
2
2x
1
k
2
x
2
1c
1
c
2
2x
#
1
c
2
x
#
2
k
1
x
o
c
1
x
#
o
cos 1u
~
u
3
2 cos u
~
u
3
sin u
~
sin 1u
~
u
3
2 sin u
~
u
3
cos u
~
u
~
m
3
gL
g
cos 1u
~
u
3
2 0
c
5
L cos 1u
~
u
3
23y
#
3
L cos 1u
~
u
3
24
c
t3
u
#
3
c
4
L sin 1u
~
u
3
23x
#
3
Lu
#
3
sin 1u
~
u
3
24
k
5
L cos 1u
~
u
3
23y
3
L sin 1u
~
u
3
24
k
4
L sin 1u
~
u
3
23x
3
L cos 1u
~
u
3
24
1J
3g
m
3
L
g
2
2u
$
3
m
3
L
g
3x
$
3
sin 1u
~
u
3
2 y
$
3
cos 1u
~
u
3
24 k
t3
1u
~
u
3
2
c
5
3y
3
#
Lu
#
3
cos 1u
~
u
3
24m
3
g
m
3
3y
$
3
L
g
u
$
3
cos 1u
~
u
3
2 L
g
u
#
3
2
sin 1u
~
u
3
24 k
5
1y
3
L sin 1u
~
u
3
24
k
4
L cos 1u
~
u
3
2 1c
3
c
4
2x
#
3
c
3
x
#
2
c
4
Lu
#
3
sin 1u
~
u
3
2 0
m
3
3x
$
3
L
g
u
$
3
sin 1u
~
u
3
2 L
g
u
#
3
2
cos 1u
~
u
3
24 1k
3
k
4
2x
3
k
3
x
2
m
2
x
$
2
1k
2
k
3
2x
2
k
2
x
1
k
3
x
3
1c
2
c
3
2x
#
2
c
2
x
#
1
c
3
x
#
3
0
m
1
x
$
1
1k
1
k
2
2x
1
k
2
x
2
1c
1
c
2
2x
#
1
c
2
x
#
2
k
1
x
o
c
1
x
#
o
Q
i
0
i 1, 2, . . ., 5
d
dt
a
0T
0u
#
3
b
0T
0u
3
0D
0u
#
3
0V
0u
3
Q
5
d
dt
a
0T
0y
#
3
b
0T
0y
3
0D
0y
#
3
0V
0y
3
Q
4
7.2 Governing Equations 367
(k)
Equation (k) is assembled in the following matrix form
(l)
where
It is clear from Eq. (l) that the system inertia, damping, and stiffness matrices
are symmetric matrices. Equation (l) is a system of five second-order ordinary
differential equations that is used to study “small” motions about the nominal
Q
5
ˆ
m
3
gL
g
cos u
~
k
t3
u
~
1k
4
k
5
2L
2
sin u
~
cos u
~
k
55
k
t3
k
4
L
2
1sin
2
u
~
cos
2
u
~
2 k
5
L
2
1cos
2
u
~
sin
2
u
~
2 m
3
gL
g
sin u
~
c
55
c
t3
c
4
L
2
sin u
~
c
5
L
2
cos u
~
e
k
1
x
o
c
1
x
#
o
0
k
4
L cosu
~
m
3
g k
5
L sinu
~
Q
ˆ
5
u
E
k
1
k
2
k
2
000
k
2
k
2
k
3
k
3
00
0 k
3
k
3
k
4
0 k
4
L sin u
~
00 0 k
5
k
5
L cos u
~
00k
4
L sin u
~
k
5
L cos u
~
k
55
Ue
x
1
x
2
x
3
y
3
u
3
u
E
c
1
c
2
c
2
000
c
2
c
2
c
3
c
3
00
0 c
3
c
3
c
4
0 c
4
L sin u
~
00 0 c
5
c
5
L cos u
~
00c
4
L sin u
~
c
5
L cos u
~
c
55
Ue
x
#
1
x
#
2
x
#
3
y
#
3
u
#
3
u
E
m
1
00 0 0
0 m
2
000
00 m
3
0 m
3
L
g
sin u
~
00 0 m
3
m
3
L
g
cos u
~
00m
3
L
g
sin u
~
m
3
L
g
cos u
~
J
3g
m
3
L
g
2
Ue
x
$
1
x
$
2
x
$
3
y
$
3
u
$
3
u
m
3
gL
g
cos u
~
k
t3
u
~
1k
4
k
5
2L
2
sin u
~
cos u
~
m
3
gL
g
u
3
sin u
~
c
4
L sinu
~
3x
#
3
Lu
#
3
sin u
~
4 c
5
L cos u
~
3y
#
3
Lu
#
3
cos u
~
4
k
4
L
2
u
3
cos
2
u
~
k
5
L cos u
~
3y
3
Lu
3
cos u
~
4 k
5
L
2
u
3
sin
2
u
~
c
t3
u
#
3
k
4
L sin u
~
3x
3
Lu
3
sin u4
1J
3g
m
3
L
g
2
2u
$
3
m
3
L
g
3x
$
3
sinu
~
y
$
3
cos u
~
4 k
t3
u
3
c
5
3y
3
#
Lu
#
3
cos u
~
4m
3
g k
5
L sin u
~
m
3
3y
$
3
L
g
u
$
3
cosu
~
4 k
5
3y
3
Lu
3
cosu
~
4
368 CHAPTER 7 Multiple Degree-of-Freedom Systems

position u
˜
. It is noted that this position is not an equilibrium position, but
rather an operating point where 0. It is noted that depending on the
application, linearization of a nonlinear system may need to be carried out
about a reference position different from the equilibrium position.
7.3 FREE RESPONSE CHARACTERISTICS
In this section, we examine the natural frequencies and mode shapes of un-
damped and damped systems. As in the case of single degree-of-freedom
systems, when the forcing is absent, the responses exhibited by a multi-degree-
of-freedom system are called free responses. In Sections 7.3.1 and 7.3.2, un-
damped systems are considered and characteristics such as natural frequencies
and mode shapes are examined. Following this discussion, modes of damped
systems are examined in Section 7.3.3, and the notion of proportional damping
is introduced. Subsequently, conservation of energy during free oscillations of
a multi-degree-of-freedom system is examined. Throughout Section 7.3, char-
acteristics of free responses of multi-degree-of-freedom systems are examined
without explicitly determining the solution for the response. In Section 7.4, we
study the vibrations of rotating shafts. In Section 7.5, we briefly discuss how
the stability of a multi-degree-of-freedom system is assessed.
7.3.1 Undamped Systems: Natural Frequencies
and Mode Shapes
For illustration, consider the system of equations given by Eq. (7.3), which
govern the motion of a linear multi-degree-of-freedom system. Setting the
damping, the circulatory and gyroscopic terms, and the external forces to
zero, and replacing q
i
by x
i
, we obtain
(7.22)
Since the system given by Eq. (7.22) is a linear system of ordinary differen-
tial equations with constant coefficients, the solution for Eq. (7.22) is as-
sumed to be of the form
15
(7.23a)
where t is time, the exponent l can be complex valued, and the displacement
vector {x} and the constant vector {X} are given by
(7.23b)5x6 d
x
1
1t 2
x
2
1t 2
o
x
N
1t 2
t
and
5X6 d
X
1
X
2
o
X
N
t
5x1t26 5X6e
lt
3M 45x
$
6 3K45x6 506
u
~
#
7.3 Free Response Characteristics 369
15
For a solution of the form of Eq. (7.25a), we note that the ratio of any two elements x
j
(t)/x
k
(t)
X
j
/X
k
is always time independent. This type of motion is called synchronous motion because both
generalized coordinates have the same time dependence.
