Balakumar Balachandran, Magrab E.B. Vibrations
Подождите немного. Документ загружается.

and
Nm/rad3K
t
4 H
51 51000000
51 102 5100000
0 51 102 510000
0051 102 51000
00051 102 51 0 0
000051 117 66 0
0000066 81 15
00000015 15
X 10
6
430 CHAPTER 7 Multiple Degree-of-Freedom Systems
7.40
Consider the system shown in Figure E7.40.
(a) Determine the equations of motion for the system
and put them in matrix form. (b) From the results ob-
tained in part (a), obtain the determinant form of the
characteristic equation.
spring of constant k, as shown in Figure E7.41. If
J
O
10 kg m
2
, r 0.25 m, k
t
600 Nm/rad, k
1000 N/m, and a 0.15 m, then determine the natural
frequencies of the system.
#
1
2
3
4
5
6
7
8
123456 8
7
Generator
FIGURE E7.39
FIGURE E7.40
FIGURE E7.41
r
1
k
1
J
1
1
r
2
k
2
k
3
J
2
2
k
t
k
t
k
J
o
r
a
J
o
r
a
Top view
Side view
Determine the natural frequencies and mode shapes
associated with the system and plot the mode shapes.
Does the system have any rigid-body modes?
7.41 Two identical discs of rotary inertia J
O
and radius
r are mounted on identical shafts and undergo tor-
sional oscillations. Each shaft has a torsional spring
constant k
t
. At a radial distance a from their respective
centers, the rotors are connected via a translation
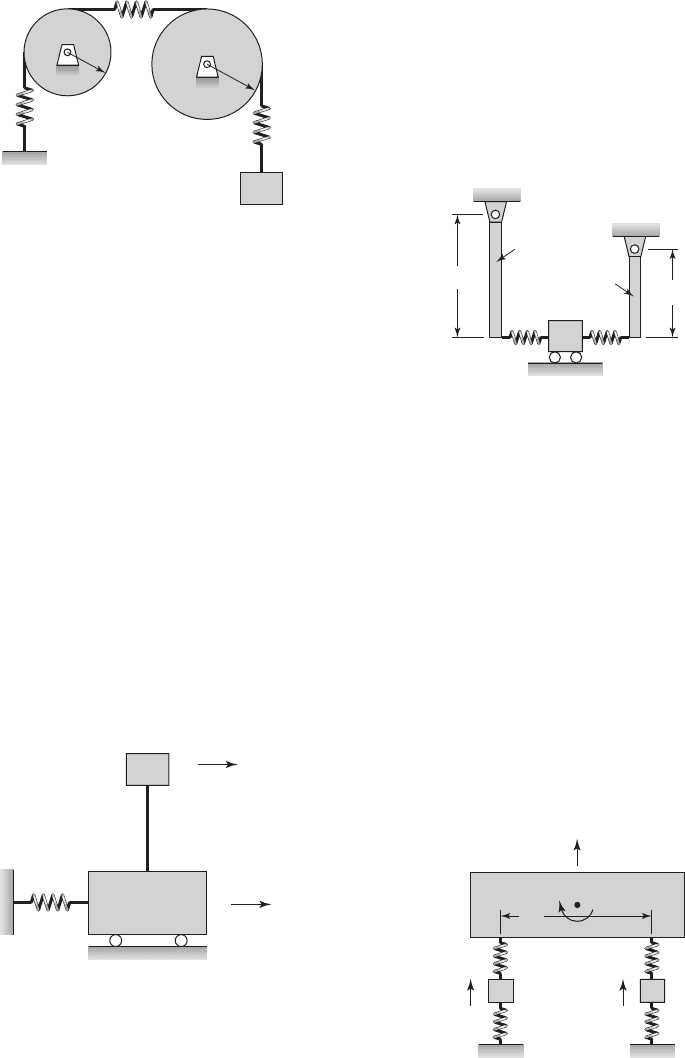
7.42 A cable fixed at one end and carrying a mass m at
the other end is stretched over two pulleys, as shown
in Figure E7.42. The pulleys have rotary inertia J
1
and
J
2
about their respective rotation centers, and the cor-
responding radii are r
1
and r
2
, respectively. The stiff-
ness of the various sections of the cables is provided
in the figure. Assume that there is sufficient friction so
that the cable does not slip on the pulleys.
a) Determine the equations governing this vibratory
system and place them in matrix form.
b) If m 12 kg, J
1
0.2 kg m
2
, J
2
0.3 kg m
2
, r
1
120 mm, r
2
160 mm, k
1
k
3
25 10
3
N/m,
and k
2
40 10
3
N/m, determine the natural fre-
quencies and mode shapes.
7.43 An electrical motor and pump system operates at
1800 rpm, and they are elastically mounted to a sup-
port structure. The mass of the system is m
1
25 kg
and the effective viscous-damping factor of the mount
is 0.15. Unfortunately, it is found that 1800 rpm coin-
cides with the natural frequency v
n1
of the system and
the horizontal amplitude of the system is excessive.
To decrease the magnitude of the horizontal ampli-
tude, it is decided that rather than change the stiffness
of the support a second mass m
2
0.25 kg will be
added to the system by attaching m
2
to the end of a
cantilever beam, as shown in Figure E7.43. The can-
tilever beam is a solid circular rod 6 mm in diameter.
Use E 1.96 10
11
N/m
2
for the Young’s modulus
of elasticity of the beam material. What should be the
length of the rod so that the natural frequencies of the
modified system are not in the range v
n1
4%?
Exercises 431
FIGURE E7.42
FIGURE E7.43
FIGURE E7.44
m
r
1
J
1
J
2
r
2
k
3
k
2
k
1
x
1
k
1
x
2
m
1
m
2
k
c
a) Use Lagrange’s equations to derive the equations
of motion. Include the effects of gravity. Put the re-
sults in matrix form.
b) For m
1
10 kg, m
2
15 kg, m
3
5 kg, k
1
k
2
100 N/m, L
1
0.5 m, and L
2
0.4 m, determine
the natural frequencies and mode shapes of the
system.
k
2
k
1
m
1
m
2
L
2
L
1
m
3
7.44 Consider the coupled pendulum system shown in
Figure E7.44.
7.45 One model that has been used to study the vibra-
tory motion of motor vehicles is shown in Figure
E7.45. The body of the vehicle has a mass m
1
and a ro-
tary inertia J
G
about an axis through the center. The
elasticity of the tires is represented by springs k
2
, and
the elasticity of the suspension by springs k
1
. The
mass of the tire assemblies is m
2
.
a) Determine the matrix form for the governing equa-
tions of the system.
b) Obtain the natural frequencies and mode shapes
for the case where m
1
800 kg, m
2
25 kg,
k
1
60 kN/m, k
2
20 kN/m, L 1.4 m, and
J
G
180 kg m
2
.
#
x
1
x
2
x
3
k
1
k
1
k
2
k
2
m
1
, J
G
G
m
2
m
2
2L
FIGURE E7.45
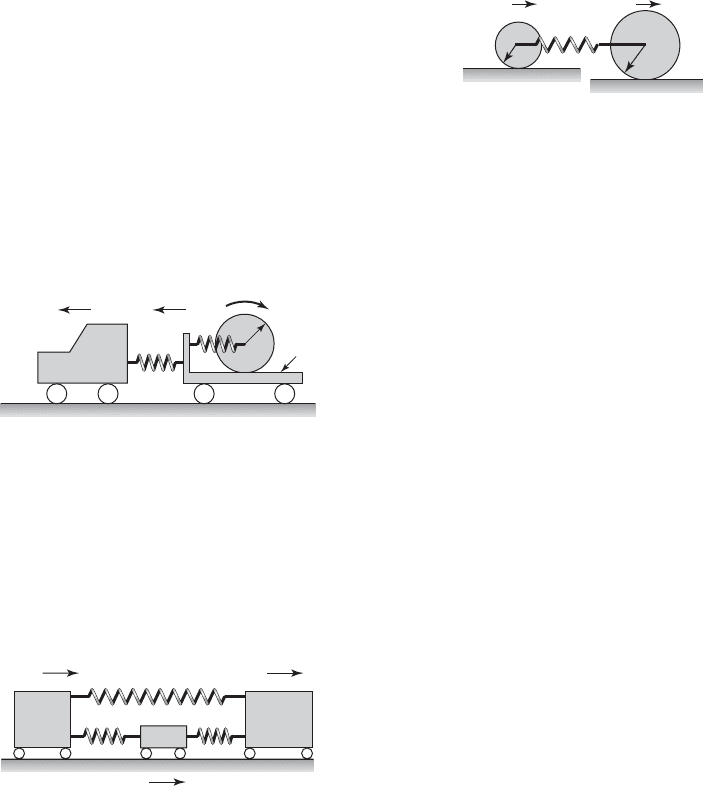
7.46 A tractor-trailer is hauling a large cylindrical
drum that is elastically supported by spring k
2
as
shown in Figure E7.46. The drum rolls on the floor of
the trailer without slipping. The trailer is attached to
the tractor by a system that has an equivalent spring
k
1
. The mass of the tractor is m
1
, that of the trailer is
m
2
, and that of the drum is m
3
.
a) Obtain the equations of motion for this system.
b) If k
1
k
2
k, m
1
m
2
m, and m
3
2m/3, then
obtain the natural frequencies in terms of k/m and
the corresponding mode shapes.
432 CHAPTER 7 Multiple Degree-of-Freedom Systems
7.50
Is it possible for a three degree-of-freedom sys-
tem to have the following eigenvectors?
Section 7.3.3
7.51 Determine the modal mass, modal stiffness, and
modal damping factors associated with the system
whose mass matrix, stiffness matrix, and damping
matrix are given by the following:
7.52 Show that the system treated in Example 7.21 is
proportionally damped by making use of Eqs. (7.99).
7.53 To describe the vertical motions of an automo-
bile, the two degree-of-freedom system shown in Fig-
ure E7.53 is used. This model is known as a quarter-
car model. If the parameters of the system are m
1
80 kg, m
2
1100 kg, k
2
30 kN/m, k
1
300 kN/m,
and c
1
5000 N/(m/s), determine if the system is pro-
portionally damped.
7.54 The modal matrix and the damping matrix for a
two degree-of-freedom system are, respectively,
Is this system proportionally damped?
7.55 For the system shown in Figure E7.12, assume
that the drive torque M
o
(t) 0. Let J
o1
1 kg m
2
,
#
3£ 4 c
1 1
11
d
and
3C 4 c
50
00
d
3C 4 c
3 2
26
d
3M 4 c
10
02
d,
3K 4 c
1 1
12
d,
5X6
1
c
1
1
1/2
s,
5X6
2
c
1
1
1/2
s,
5X6
3
c
0
2
1
s
FIGURE E7.46
k
1
k
2
x
1
x
2
r
m
1
m
3
m
2
FIGURE E7.47
FIGURE E7.48
7.47 Determine the characteristic equation for the
system shown in Figure E7.47 and solve this equation
for the special case when k
1
k
2
k
3
k and m
1
m
2
m
3
m. Determine if the system has any
rigid-body modes.
k
2
k
3
k
1
m
3
m
2
x
2
x
3
x
1
m
1
x
1
x
2
r
2
r
1
k
J
1
, m
1
J
2
, m
2
7.48 Two disks that roll without slipping on a flat sur-
face are connected to each other by a spring with con-
stant k, as shown in Figure E7.48. Determine the nat-
ural frequencies and mode shapes of the system.
Section 7.3.2
7.49 Show that the linear independence of eigen-
vectors given by Eq. (7.72) is true by making use of
the orthogonality property of eigenvectors.
J
o2
4 kg m
2
, J
o3
1 kg m
2
and the torsional stiff-
ness of each shaft be as follows: k
t1
k
t2
10 Nm/rad
and k
t3
5 Nm/rad. In addition, let the damping
coefficients be such that c
t1
0.5 Nm/rad/s, c
t2
2 Nm/rad/s, and c
t3
0.5 Nm/rad/s. Determine the
following:
a) Is the system proportionally damped?
b) If the damping associated with the second fly-
wheel changes from 2 Nm/rad/s to 1.8 Nm/rad/s,
can the system be approximated as a system with
modal damping?
7.56 The eigenvalues associated with a damped three
degree-of-freedom system are given by the following:
l
d3
1,2
0.4 j1.960
l
d2
1,2
0.75 j1.299
l
d1
1,2
0.1 j0.995
##
Exercises 433
FIGURE E7.53
k
1
k
2
c
2
m
2
m
1
Automobile
body (sprung
mass)
Suspension
Axle and wheel
mass (unsprung
mass)
Tire stiffness
Determine the system natural frequencies, modal
damping factors, and damped natural frequencies.
Section 7.3.4
7.57 Consider free oscillations of the gyro-sensor
treated in Example 7.4 and determine if energy is
conserved in the system.
7.58 Consider the three degree-of-freedom system
shown in Figure E7.31 and determine if the linear
momentum and the total energy of this system are
conserved.
Section 7.5
7.59 The eigenvalues determined for two different
three degree-of-freedom systems are as follows:
a)
b)
Determine which of these systems is stable.
l
d3
1,2
a
3
,b
3
;
a
3
0, b
3
0
l
d2
1,2
a
2
jb
2
;
a
2
0, b
2
0
l
d1
1,2
a
1
jb
1
;
a
1
0, b
1
0
l
d3
1,2
a
3
jb
3
;
a
3
0, b
3
0
l
d2
1,2
a
2
jb
2
;
a
2
0, b
2
0
l
d1
1,2
a
1
jb
1
;
a
1
0, b
1
0

434
The transmission of undesired vibrations can be attenuated by various techniques, one of which is based on the principle of the vibra-
tion absorber. The attachment of an elastically supported mass creates a tuned mass absorber that reduces vibration levels in systems
excited at a constant frequency. An externally energized elastically mounted mass whose motion is controlled in a specific manner is a
more sophisticated version of the tuned mass absorber. (Source: Kristiina Paul; © Justin Kase / Alamy)

435
8
Multiple Degree-of-Freedom Systems:
General Solution for Response and
Forced Oscillations
8.1 INTRODUCTION
8.2 NORMAL-MODE APPROACH
8.2.1 General Solution
8.2.2 Response to Initial Conditions
8.2.3 Response to Harmonic Forcing and the Frequency-Response Function
8.3 STATE-SPACE FORMULATION
8.4 LAPLACE TRANSFORM APPROACH
8.4.1 Response to Arbitrary Forcing
8.4.2 Response to Initial Conditions
8.4.3 Force Transmitted to a Boundary
8.5 TRANSFER FUNCTIONS AND FREQUENCY-RESPONSE FUNCTIONS
8.6 VIBRATION ABSORBERS
8.6.1 Linear Vibration Absorber
8.6.2 Centrifugal Pendulum Vibration Absorber
8.6.3 Bar Slider System
8.6.4 Pendulum Absorber
8.6.5 Particle Impact Damper
8.7 VIBRATION ISOLATION: TRANSMISSIBILITY RATIO
8.8 SYSTEMS WITH MOVING BASE
8.9 SUMMARY
EXERCISES
8.1 INTRODUCTION
In the previous chapter, we studied systems with multiple degrees of freedom
and discussed the ways in which one can obtain the governing equations of
motion. In addition, free-response characteristics of damped and undamped
systems were examined. In this chapter, we build on this material, and as laid

out in Table 8.1, employ different approaches to obtain the solution for the re-
sponses of multi-degree-of-freedom systems.
As with the case of a single degree-of-freedom system, there are differ-
ent approaches to determine the response of a multiple degree-of-freedom-
system. These approaches include the following: (a) normal-mode approach,
(b) Laplace transform approach, and (c) state-space formulation. The first
approach is unique to multiple degree-of-freedom-systems, while the second
and third approaches are similar in spirit to those used for single degree-of-
freedom systems. It is remarked that unlike the other two approaches, the
Laplace transform approach is not based in the time domain but, instead, this
approach is based in the Laplace domain.
With the objective of providing a summary of the domain of applicabil-
ity of the above-mentioned approaches, Table 8.1 has been constructed. This
summary is organized around a) whether the system is linear or nonlinear and
b) the nature of the damping properties of the system.
436 CHAPTER 8 Multiple Degree-of-Freedom Systems
TABLE 8.1
Application Domains of Different
Solution Methods for Multiple
Degree-of-Freedom Systems
Typically Used
to Determine
System Methods the Following Comments Section
Linear Normal-mode Natural frequencies, For damped systems 8.2
systems approach mode shapes, and with given initial
responses of inertial conditions and
elements to initial forcing; requires
conditions and special form of
external forcing linear viscous
damping matrix—
analytical and
numerical solutions
Laplace transform Natural frequencies, Cumbersome for 8.4
approach transfer functions, systems with high
and responses of degrees of
inertial elements to freedom—
initial conditions analytical and
and external forcing numerical
for general form of solutions
damping matrix
State-space Responses of inertial Analytical and 8.3
formulation elements to initial numerical
conditions and solutions
external forcing for
general form of
damping matrix
Nonlinear Weakly nonlinear Responses of inertial For “strongly”
systems analysis and elements to initial nonlinear systems,
numerical conditions and usually, only
approach external forcing possible to get
for arbitrary a numerical
damping models solution
As presented in Table 8.1, all three approaches can be used to study sys-
tems subjected to periodic and other excitations. However, the form of the
damping matrix places a restriction on the domain of applicability of the
normal-mode approach. As discussed in Chapter 7 and elaborated further in
this chapter, the damping matrix needs to have a special structure in order to
use the normal-mode approach. However, whenever this approach is applica-
ble, the solution obtained through this approach provides insight into the
spatial responses of the inertial elements. This type of information is indis-
pensable for system designs where one is minimizing or maximizing the re-
sponse to external excitations and where one is determining where to place an
actuator and/or a sensor.
The Laplace transform approach is convenient to use since one can
obtain transfer functions and frequency-response functions, which can be
used to design systems such as vibration absorbers and mechanical filters. In
addition, an attractive feature of this approach is that there is no restriction on
the form of damping. However, for systems with more than two degrees of
freedom, the algebra is cumbersome. The Laplace transform approach is lim-
ited to linear vibratory systems.
The state-space formulation, where the governing equations are put in
first-order form, lends itself to an analytical solution in linear cases and to
numerical solutions in both linear and nonlinear cases. This formulation is
applicable to systems with all forms of damping and forcing. For the nonlin-
ear systems presented in this book, only numerical solutions are pursued,
although methods to determine analytical approximations exist for “weakly”
nonlinear systems.
1
Whenever one is seeking a solution of a nonlinear system,
it is important to note that the approach is based in the time domain.
After presenting the different approaches to determine the response of a
multiple degree-of-freedom system, we present transfer functions and the re-
lationship between the frequency-response function and the transfer function
in the same manner as was done for single degree-of-freedom systems. In the
latter part of the chapter, we introduce vibration absorbers, the notion of trans-
missibility ratio, and examine systems subjected to base excitation.
In this chapter, we shall show how to:
• Use normal modes, Laplace transforms, and the state-space formulation to
determine the responses of multiple degree-of-freedom systems to initial
displacements, initial velocities, and external forces.
• Determine the frequency-response functions for two degree-of-freedom
systems.
• Examine different types of vibration absorbers and identify and choose
the appropriate parameters to obtain an optimal performance.
• Isolate the force transmitted to the stationary boundary of two degree-of-
freedom systems.
• Analyze the responses of two degree-of-freedom systems with a moving
base.
8.1 Introduction 437
1
A. H. Nayfeh and D. T. Mook, Nonlinear Oscillations, John Wiley & Sons, NY (1979).

8.2 NORMAL-MODE APPROACH
8.2.1 General Solution
In Section 7.3, we discussed the characteristics associated with free oscilla-
tions of multiple degree-of-freedom systems such as natural frequencies and
mode shapes without explicitly determining them. In this section, we deter-
mine the general solution for the response of a multi-degree-of-freedom
system and present explicit forms for the responses due to both forcing and
initial conditions. This development follows along the lines of Appendix D,
except that one now needs to consider spatial information apart from time
information.
In this section, we determine the response of the system given by
Eq. (7.3), which is repeated below after replacing q
i
(t) by x
i
(t), {Q} by {F},
and dropping the gyroscopic and circulatory force terms.
(8.1)
In general, Eq. (8.1) is a coupled system of equations. One way to solve this
system is to uncouple them by using an appropriate coordinate transfor-
mation. One candidate transformation is the modal matrix given by
Eq. (7.31), which has the desirable property of being orthogonal to the matri-
ces and . Thus, we assume a solution to Eq. (8.1) of the form
(8.2)
Modal Modal
matrix amplitudes
where {h(t)} is a column vector of generalized (modal) coordinates that are
to be determined. On substituting Eq. (8.2) into Eq. (8.1), we obtain
(8.3)
Pre-multiplying Eq. (8.3) by results in
(8.4)
Upon using Eqs. (7.68), we obtain
(8.5)
We now pre-multiply Eq. (8.5) by , the inverse of , and use
Eq. (7.69) to arrive at
(8.6)
where we have assumed that exists and reintroduced the force vector
{Q} so that
(8.7)
Equations (8.6) and (8.7) are written in expanded form as
5Q6 3M
D
4
1
3£ 4
T
5F6
3M
D
4
1
5h
$
6 3M
D
4
1
3£ 4
T
3C 43£ 45h
#
6 3v
2
D
45h6 5Q6
3M
D
43M
D
4
1
3M
D
45h
$
6 3£ 4
T
3C 43£ 45h
#
6 3K
D
45h6 3£ 4
T
5F6
3£ 4
T
3M43£ 45h
$
6 3£ 4
T
3C43£ 45h
#
6 3£ 4
T
3K43£ 45h6 3£ 4
T
5F6
3£ 4
T
3M 43£ 45h
$
6 3C43£ 45h
#
6 3K43£ 45h6 5F6
5x1t26 3£ 4 5h1t 26
3K 43M4
3£ 4
3M 45x
$
6 3C45x
$
6 3K45x6 F
438 CHAPTER 8 Multiple Degree-of-Freedom Systems
⎫
⎬
⎭
⎫
⎬
⎭
(8.8)
From the form of Eq. (8.8), it is clear that these equations in the trans-
formed coordinates can be uncoupled into N individual second-order differ-
ential equations if the matrix
is a diagonal matrix. As discussed in Section 7.3.3, this is possible when the
system is proportionally damped. For this case, we obtain from Eqs. (7.99)
and (7.102) that
(8.9)
where is the modal mass of the kth mode. From Eqs. (7.68a) and (8.9), it
follows that
(8.10)
Hence, for a system with proportional damping, from Eqs. (8.6) and
(8.10), we arrive at the uncoupled set of equations
(8.11)5h
$
6 312zv2
D
45h
#
6 3v
2
D
45h6 5Q6
≥
2z
1
v
1
0
p
0
02z
2
v
2
p
0
oo
∞
o
00
p
2z
N
v
N
¥ 312zv2
D
4
≥
2z
1
v
1
M
ˆ
11
0
p
0
02z
2
v
2
M
ˆ
22
p
0
oo
∞
o
00
p
2z
N
v
N
M
ˆ
NN
¥
3M
D
4
1
3C
D
4 ≥
1/M
ˆ
11
0
p
0
01/M
ˆ
22
p
0
oo
∞o
00
p
1/M
ˆ
NN
¥
M
ˆ
kk
≥
2z
1
v
1
M
ˆ
11
0
p
0
02z
2
v
2
M
ˆ
22
p
0
oo
∞
o
00
p
2z
N
v
N
M
ˆ
NN
¥
3C
D
4 3£ 4
T
3C43£ 4
3M
D
4
1
3£ 4
T
3C43£ 4
≥
v
2
1
0
p
0
0 v
2
2
p
0
oo
∞
o
00
p
v
2
N
¥µ
h
1
1t 2
h
2
1t 2
o
h
N
1t 2
∂ µ
Q
1
1t 2
Q
2
1t 2
o
Q
N
1t 2
∂
≥
10
p
0
01
p
0
oo∞o
00
p
1
¥µ
h
$
1
1t 2
h
$
2
1t 2
o
h
$
N
1t 2
∂ 3M
D
4
1
3£ 4
T
3C43£ 4µ
h
#
1
1t 2
h
#
2
1t 2
o
h
#
N
1t 2
∂
8.2 Normal-Mode Approach 439
