Balakumar Balachandran, Magrab E.B. Vibrations

Подождите немного. Документ загружается.

where a and b are real-valued constants. Since, in Eq. (7.83), the damping

matrix is a combination of a matrix proportional to the mass matrix

and a matrix proportional to a stiffness matrix , we use the designation

proportional damping.

On substituting Eq. (7.83) into Eq. (7.81), we arrive at the eigenvalue

problem

(7.84)

which is rewritten in the form

(7.85)

Next, we compare the eigenvalues l

of the proportionally damped system

with the eigenvalues l

of the undamped system determined from Eq. (7.25).

These eigenvalues are determined by the following characteristic equations

determined from Eq. (7.26) and Eq. (7.85), respectively.

Undamped system

(7.86)

Damped system

(7.87)

When the two characteristic polynomials given by Eqs. (7.86) and (7.87) are

compared, it is clear that l

 l

; that is, the eigenvalues for the proportion-

ally damped case are not the same as those for the undamped case. Since

and are real and symmetric matrices, the eigenvalues of the undamped

system are real and l

jv

, where v

are the system natural frequen-

cies. By contrast, the eigenvalues of the proportionally damped system are

complex-valued quantities.

To carry out a proper comparison of the eigenvectors of a damped system

with those of the corresponding undamped system, the state-space formula-

tion discussed in Section 8.3 is needed. From such a formulation, it can be es-

tablished that the eigenvectors of the proportionally damped system and the

eigenvectors of the associated undamped system have a similar structure; in

particular, the ratios of the modal components corresponding to the displace-

ment states are the same in the undamped and damped cases.

This informa-

tion will now be used to determine the relationship between l

and l

Let {X}

be the eigenvector associated with the eigenvalue of the un-

damped system described by Eq. (7.25). Then, setting l  l

and {X} 

{X}

in Eq. (7.85) we obtain

(7.88)

Pre-multiplying Eqs. (7.88) by {X}

, we arrive at

311  bl

23K 4 l

 a23M 445X6

 506

k  1, 2, . . ., N

3M 4

3K 4

det 311  bl23K 4 l1l  a23M 44 0

det 33K 4 l

3M 44 0

311  bl23K4 l1l  a23M445X6 506

3M 4 la3M4 bl3K4 3K 445X6 506

3K 4

3M 43C 4

400 CHAPTER 7 Multiple Degree-of-Freedom Systems

P. C. Müller and W. O. Schiehlen, ibid.

(7.89)

which, upon expanding the different terms, leads to

(7.90)

Making use of Eqs. (7.67) for the modal mass and the modal stiffness

in Eqs. (7.90), we ﬁnd that

(7.91)

The natural frequency associated with the kth mode is given by Eqs. (7.66);

that is,

(7.92)

Then, Eqs. (7.91) become the quadratic equations

(7.93a)

whose roots are given by

(7.93b)

Thus, Eqs. (7.93b) establish how the eigenvalues l

of the proportionally

damped system are related to the eigenvalues l

jv

of the undamped

system.

Equations (7.93a), which are associated with the free oscillation of the

kth mode of the proportionally damped system, has the same form of the char-

acteristic equation obtained for a single degree-of-freedom system; that is,

Eq. (4.49). Comparing these two equations, we introduce the modal damping

factor z

associated with the kth mode as

(7.94)

From Eq. (7.94), we see that if b  0, then z

 a/v

and z

decreases as

increases. On the other hand, when a  0, z

 bv

and z

increases as v

increases.

In terms of the modal damping factor, one can rewrite Eqs. (7.93a) as

(7.95)

Hence, if the damping factor z

of the kth mode is such that 0  z

 1, then

one can deﬁne the corresponding damped natural frequency of the system as

(7.96)

The roots of Eqs. (7.93a), given by Eqs. (7.93b), are expressed in terms

of the damping factor z

, the natural frequency v

, and the damped natural fre-

quency v

(7.97)l

1,2

z

 jv

 v

21  z

 2z

 v

 0

k  1, 2, . . ., N



 bv

k  1, 2, . . ., N

1,2



c1a  bv

2 21a  bv

 4v

k  1, 2, . . ., N

 1a  bv

 v

 0

k  1, 2, . . ., N



k  1, 2, . . ., N

11  bl

 l

 a2M

 0

k  1, 2, . . ., N

11  bl

25X6

3K 45X6

 l

 a25X6

3M 45X6

 0

k  1, 2, . . ., N

5X6

311  bl

23K 4 l

 a23M 445X6

 5X6

506

k  1, 2, . . ., N

7.3 Free Response Characteristics 401

Examining Eqs. (7.97), it is clear that the real parts of the complex-conjugate

pair of eigenvalues associated with a particular mode contain information

about the associated damping factor and undamped natural frequency and that

the imaginary parts of these eigenvalues contain information about the asso-

ciated damped natural frequency.

From Eqs. (7.93), it is also clear that the characteristic polynomial asso-

ciated with the proportionally damped system is of the form

(7.98)

In other words, Eq. (7.98) is the result of expanding the determinant given in

Eq. (7.87) in terms of N quadratic polynomials, each being associated with an

equivalent single degree-of-freedom system in the considered mode of free

oscillation. The interpretation of the modal damping factors of the different

modes and the associated damped natural frequencies will be further clariﬁed

in Section 8.2, when presenting the normal-mode approach.

In Section 7.3.2, we saw that the modal matrix , which consisted of

the N eigenvectors determined for the undamped system, is used to establish

the diagonal inertia matrix and the diagonal stiffness matrix by

making use of the orthogonality of the eigenvectors. Similarly, for a propor-

tionally damped system, the damping matrix given by Eq. (7.83) can be

transformed to a diagonal matrix . To examine this, let us start from

(7.99)

Then substituting from Eq. (7.83) into Eq. (7.99), we arrive at

(7.100)

where we have made use of Eqs. (7.68) and (7.69). On expanding the right-

hand side of Eq. (7.100), we have that

(7.101)

from which it is clear that we have a diagonal damping matrix [C

] for a pro-

portionally damped system. The matrix [C

] is rewritten in terms of the modal

damping factors given by Eqs. (7.94) as

(7.102)3C

4 D

02z

oo∞o

4 ≥

1a  bv

0 1a  bv

oo∞o

1a  bv

 3a 3I 4 b 3v

443M

 a3M

4 b3K

4 a3M

4 b3v

43M

4 3£ 4

3a 3M 4 b3K443£ 4 a3£ 4

3M 43£ 4 b3£ 4

3K 43£ 4

4 3£ 4

3C 43£ 4

3C 4

43M

3£ 4

. . . 1l

 1a  bv

 v

2 0

 1a  bv

 v

21l

 1a  bv

 v

402 CHAPTER 7 Multiple Degree-of-Freedom Systems

On examining the form of Eq. (7.102), it is clear that each of the diagonal

terms is an equivalent damping coefﬁcient associated with a certain damping

mode. The transformation given by Eq. (7.99) can also be used to determine

if the damping matrix for a system can be labeled as a proportional damping

matrix. In other words, if the resulting transformed damping matrix is a diag-

onal matrix, then the system is proportionally damped; in all other cases, the

transformed matrix is not a diagonal matrix.

Lightly Damped Systems and Other Cases

There are lightly damped systems (0  z  0.1) in which does

not result in a diagonal matrix.

In this case, the off-diagonal terms are neg-

lected, and only the diagonal terms

are retained. In this case,

the damping factor z

takes the form

(7.103)

Another case of interest is one where the damping factor is constant and

equal for each mode. In this case, the modal damping factor is assumed to be

(7.104)

The last case that we shall consider corresponds to the physical system

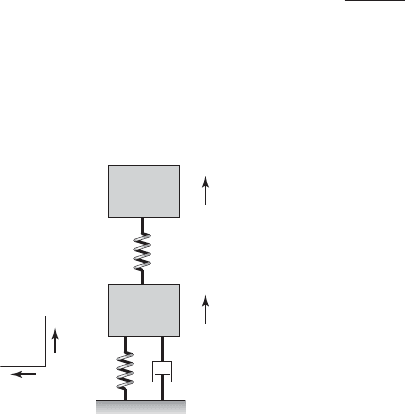
shown in Figure 7.21, which is used as a vibratory model of such diverse

systems as an animal paw

or a system with a vibration absorber, which is

discussed in Section 8.6. For this two degree-of-freedom system, the damp-

ing matrix and the modal damping are given by, respectively,

(7.105)

Making use of Eqs. (7.105), the matrix is determined as

(7.106)

Thus, we see that for a two degree-of-freedom system where one damper is

connected to only one inertial element, the resulting transformed matrix is a

 c

3£ 4

3C 43£ 4 c

3£ 4

3C 43£ 4

3£ 4 c

3C 4 c

3£ 43C 4

 z

k  1, 2, . . ., N



13£ 2

3C 43£ 42

13£ 4

3C 43£ 42

3£ 4

3C 43£ 4

7.3 Free Response Characteristics 403

J. H. Ginsberg, Mechanical and Structural Vibrations, John Wiley & Sons, NY, Chapter 4

(2001).

R. M. Alexander, Elastic Mechanisms in Animal Movement, Cambridge University Press, Cam-

bridge, Great Britain, Chapter 7 (1988).

FIGURE 7.21

Vibratory model of a two

degree-of-freedom system with

one damper.

nondiagonal matrix. This information is useful for deciding which approach

to use in determining a solution for the response of a multiple degree-of-

freedom system, as discussed in Chapter 8.

EXAMPLE 7.21

Nature of the damping matrix

For the following mass, stiffness, and damping matrices, we shall determine

whether the system has proportional damping.

(a)

To determine whether the damping matrix is proportional, we consider

Eq. (7.83) and determine if there are constants a and b for which the damp-

ing matrix in Eq. (a) is written as

(b)

Comparing the elements of matrix from the third equation of Eqs. (a) with

those of Eq (b), we obtain

(c)

from which we ﬁnd that a  0.2 and b  0.2. Therefore, it is possible to ex-

press the damping matrix in the form of Eq. (7.83), and hence, the given

damping matrix represents proportional damping.

EXAMPLE 7.22

Free oscillation characteristics of a proportionally damped system

We revisit Example 7.21 to determine the characteristic equation associated

with this system, and from this equation, we solve for the eigenvalues associ-

ated with the damped system. We shall illustrate how the modal damping

factors are calculated and the associated damped natural frequencies are

determined.

Undamped System

To determine the natural frequencies of the undamped system, we make use

of the stiffness and inertia matrices from Eqs. (a) of Example 7.21 and

Eq. (7.26) and obtain the following characteristic equation:

a  b  0.4

b 0.2

2 a  2b  0.8

3C 4

 c

2a  2b b

ba b

 a c

d b c

2 1

11

3C 4 a3M4 b3K4

3C 4

3M 4 c

3K 4 c

2 1

11

3C 4 c

0.8 0.2

0.2 0.4

404 CHAPTER 7 Multiple Degree-of-Freedom Systems

(a)

Equation (a) leads to the quartic equation

(b)

whose roots are

(c)

Since and are real symmetric matrices, the eigenvalues are real. To

determine the associated natural frequencies, one can use Eq. (7.35)—that is,

v

—and obtain

rads/s

rads/s (d)

Damped System

From Eq. (7.81) and Eqs. (a) of Example 7.21, we ﬁnd that the characteristic

equation in the proportionally damped case is given by

which is rewritten as

(e)

Expanding the determinant in Eq. (e), we arrive at the quartic polynomial

(f)

Solving

Eq. (f), we ﬁnd that the eigenvalues in the proportionally damped

case are given by

(g)l

1,2

 l

3,4

0.271  j1.278

1,2

 l

1,2

0.129  j0.526

 1.6l

 4.28l

 1.2l  1  0

det c

 0.8l  2 0.2l  1

0.2l  1 l

 0.4l  1

d 0

det cl

d l c

0.8 0.2

0.2 0.4

d c

2 1

11

dd 0



1 

 1.307



1 

 0.541

3K 43M4

a1 

 4l

 1  0

det c

21l

 12 1

1 1l

 12

d 0

det cl

d c

2 1

11

dd 0

7.3 Free Response Characteristics 405

The MATLAB function roots was used.

Equations (g) could have been obtained directly from Eqs. (7.93b) after

making use of the undamped natural frequencies given in Eqs. (d) and the val-

ues of a and b determined in Example 7.21; that is,

(h)

and

(i)

From Eq. (d), we have that v

 0.541 rad/s and v

 1.307 rad/s. Mak-

ing use of Eq. (7.97), we obtain the damping factors as z

 0.129/0.541 

0.238 and z

 0.271/1.307  0.207. The modal damping factors can also be

found from Eqs. (7.94) as

(j)

which agree with the previously determined values. Since both damping fac-

tors are less than 1, the corresponding damped natural frequencies are deter-

mined by making use of Eqs. (7.96), (d), and ( j). The calculations lead to

rad/s

rad/s (k)

EXAMPLE 7.23

Free oscillation characteristics of a system with gyroscopic forces

We revisit Example 7.4, where we discussed a gyro-sensor, and illustrate the

effects that gyroscopic forces have on the eigenvalues. The characteristic

polynomial is determined for the damped case and the eigenvalues are ex-

plicitly determined only for the undamped case.

Setting the external force f

to zero in Eq. (d) of Example 7.4, we obtain

the following system of equations:

(a)

Considering a special case where c

 c

 c and k

 k

 k in Figure 7.6;

that is, the stiffness-damper combinations are identical in both directions,

3M 4e

f 3C 4e

f 3G 4e

f 3K 4e

f e

 1.307  21  0.207

 1.279

 0.541  21  0.239

 0.525



0.2

1.307

 0.2  1.307 b 0.207



0.2

0.541

 0.2  0.541 b 0.239

0.271  j1.278

1,2



310.2  0.2  0.1.307

2 210.2  0.2  1.307

 4  1.307

0.129  j0.526

1,2



310.2  0.2  0.541

2 210.2  0.2  0.541

 4  0.541

406 CHAPTER 7 Multiple Degree-of-Freedom Systems

we ﬁnd that the different matrices in Eqs. (a) are determined from Eqs. (e)

of Example 7.4 as

(b)

To determine the eigenvalues associated with this system, we set the cir-

culatory terms and substitute Eqs. (b) into Eq. (7.77) to obtain the

characteristic equation

(c)

Equation (c) is rearranged to give

(d)

On expanding this determinant, the result is the quartic polynomial

(e)

Equation (e) is the characteristic equation for the damped system, whose four

roots are determined numerically for given values of k, c, m, and v

In order to determine the eigenvalues of the undamped system explicitly,

we set c  0 in Eq. (e) and obtain

(f)

The roots of this quadratic polynomial in l

are given by

(g)

When the gyroscopic force is zero—that is, v

 0—these results reduce to

the natural frequencies of two uncoupled single degree-of-freedom systems,

each of which has the same mass and the same stiffness. Since

then all of the eigenvalues are imaginary, as in the case of an undamped sys-

tem free of gyroscopic forces; that is, when v

 0.

 a

 v

1,2

a

 v

b 2v

 2 a

 v

 a

 v

 0

 2 a

 v

l  a

 v

 0

 2

 ca

 2

 2v

det c

 cl  k  mv

2mv

2mv

l ml

 cl  k  mv

d 0

 c

k  mv

0 k  mv

dd 0

det cl

m 0

0 m

d l ac

c 0

0 c

d c

0 2mv

2mv

3H 4 304

3C 4 c

c 0

0 c

3G 4 c

0 2mv

2mv

3M 4 c

m 0

0 m

3K 4 c

k  mv

0 k  mv

7.3 Free Response Characteristics 407

7.3.4 Conservation of Energy

In Section 7.2.1, we discussed how the linear momentum and the angular mo-

mentum of a multiple degree-of-freedom system is conserved when the ex-

ternal forces and external moments are absent. Here, we examine when the

energy of a multiple degree-of-freedom system is conserved during free os-

cillations. To this end, we start from Eq. (7.73), which are the equations for a

damped system with gyroscopic and circulatory terms; that is

Pre-multiplying this equation by , we arrive at

(7.107)

Noting that { }  0 because the gyroscopic matrix is a skew sym-

metric matrix, and expanding and rearranging Eq. (7.107) leads to

(7.108)

Since and are symmetric matrices, the left-hand side of Eq. (7.108)

is expressed in terms of a time derivative as

(7.109)

Examining Eq. (7.109), we ﬁnd that if the system is undamped and free of cir-

culatory forces, the right-hand side is zero and Eq. (7.109) becomes

(7.110)

which means that

(7.111)

Making use of Eqs. (7.8) for a natural system, we recognize that the left-hand

side of Eq. (7.111) is the sum of the system kinetic energy and the system po-

tential energy. In other words, Eq. (7.111) means that

(7.112)

where E is the total energy of the natural system. Thus, the energy of a mul-

tiple degree-of-freedom system is only conserved in the absence of damping

and circulatory forces. For nonnatural systems, the left-hand side of Eq.

(7.111) is referred to as the Hamiltonian of the system.

E  T  V  constant

3M 45x

6

5x6

3K 45x6 constant

3M 45x

6

5x6

3K 45x6b 0

3M 45x

6

5x6

3K 45x6b5x

3C 45x

6 5x

3H 45x6

3K 43M 4

3M 45x

6 5x

3K 45x65x

3C 45x

6 5x

3H 45x6

3G 45x

3M 45x

6 5x

33C 4 3G445x

6 5x

33K 4 3H445x6 506

3M 45x

6 33C4 3G 445x

6 33K4 3H 445x6 506

408 CHAPTER 7 Multiple Degree-of-Freedom Systems

L. Meirovitch, ibid.

EXAMPLE 7.24 Conservation of energy in a three degree-of-freedom system

Consider the three degree-of-freedom system used to model the milling ma-

chine shown in Figure 7.4. We set f

(t) to zero so that we can examine free os-

cillations of this system. Then, Eqs. (b) of Example 7.1 become

(a)

From the form of Eqs. (a), it is clear that the system is free of gyroscopic

and circulatory forces. However, due to the presence of damping, we see from

Eq. (7.109) that the sum of the kinetic energy of the system and the potential

energy of the system is not conserved; in other words,

 constant (b)

Making use of E  T  V to represent the total energy of the system and us-

ing Eq. (7.109), we see that

(c)

Since the value of the right-hand side of Eq. (c) is always negative, except

when (i.e., at the system’s equilibrium position), the total

energy of the system continues to decrease and eventually comes to zero at the

system’s equilibrium position. In the absence of damping, Eq. (c) becomes

(d)

and hence, energy is conserved.

7.4 ROTATING SHAFTS ON FLEXIBLE SUPPORTS

Many types of rotating machinery are mounted on a shaft, which in turn is

mounted to a supporting structure with ﬂexibility. This ﬂexibility is modeled

as springs. The masses mounted to the shaft can have slight imbalances,

 0

 x

 0

5x

3C 45x

6Bc

 x

 c

 x

 c

System potential energy

System kinetic energy



 x



 x



 C

k

 k

k

0 k

 k

s c

0 m

00m

s C

c

 c

c

0 c

 c

7.4 Rotating Shafts on Flexible Supports 409

⎫

⎪

⎬

⎪

⎭

⎫

⎪

⎬

⎪

⎭