Balakumar Balachandran, Magrab E.B. Vibrations

Подождите немного. Документ загружается.

which can cause the shaft to vibrate in an undesirable manner. In this section,

we shall model such a system and analyze it to determine the factors that in-

ﬂuence its vibratory motion.

Consider a massless rotating shaft carrying a disk of mass m, as shown in

Figure 7.22a. We ignore damping effects in this analysis, and assume “small”

angular motions of the disk, as will be explained subsequently. The external

forces and moments that act on the disk also will be discussed later. Referring

to Figure 7.22b, the center of mass of the disk is located at P, which is located

at a distance e from the center of the shaft C. In addition, the shaft is assumed

to be supported at its left and right ends by pairs of translational springs in the

x and y directions, as shown in Figure 7.23.

Kinematics and Kinetic Energy

As shown in Figure 7.22b, the unit vectors i, j, and k are directed along the

O-x, O-y, and O-z directions, and point O is ﬁxed in an inertial reference frame.

The unit vectors i, j, and k are directed along the C-x, C-y, and C-z direc-

tions, where C is the geometric center of the disk. The static unbalance angle is

410 CHAPTER 7 Multiple Degree-of-Freedom Systems

The derivation of the equations of motion follows the treatment provided in G. Genta, 1995,

ibid.

(a)

(b)

⇒











 

Rotation axis











Axis of symmetry

FIGURE 7.22

(a) Rotating shaft with disk showing supports and the x, y, and z axes of the inertial reference frame; and (b) transformation from

Oxyz to disk ﬁxed frame Cxyz and the rotation x that accounts for the angular imbalance. An Euler-angle sequence of a w rotation

about the O-x axis, followed by a u rotation about the intermediate y axis, and a subsequent rotation of q about the O-z axis takes

one from the Oxyz frame to the Cxyz frame shown in Figure 7.22b. A subsequent rotation x about the C-y axis takes one to the

principal axes of the disk.

a and x is the angular imbalance between the axis of symmetry and the rota-

tion axis, which is along the C-z direction. The axis of symmetry is shown in

Figure 7.22b. In the absence of this angular imbalance x, the principal axes of

the disk coincide with the C-x, C-y, and C-z axes.

To obtain the equations of motion, we use Lagrange’s equations. We ﬁrst

construct the kinetic energy and potential energy of the system. In order to go

from the Oxyz frame to the Cxyz frame, an Euler-angle sequence consist-

ing of a w rotation about the O-x axis, followed by a u rotation about the in-

termediate y axis, and a subsequent rotation of q about the O-z or C-z axis is

used. For an arbitrary rotation b about each of these three axes, we can deﬁne

the rotation matrices as follows.

1. For a rotation b about the O-x axis,

(7.113a)

2. For a rotation b about the intermediate y axis,

(7.113b)

3. For a rotation b about the O-z axis,

(7.113c)

Making use of the rotation matrices given in Eq. (7.113), one can relate

the unit vectors i, j, and k to the unit vectors i, j, and k as

(7.114)

where we have assumed “small” rotation angles w and u about zero in arriv-

ing at the composite rotation matrix. In addition, if it is assumed that the static

 C

cos 1q  a2 wu cos 1q  a 2 sin 1q  a 2 w sin 1q  a2 u cos 1q  a2

sin 1q  a2 wu sin 1q  a2 cos 1q  a2

w cos 1q  a2 u sin 1q  a 2

u w 1

i¿

j¿

k¿

s 3R

1q  a243R

1u 243R

1w 24c

1b 24 C

cos b sin b 0

sin b cos b 0

001

1b 24 C

cos b 0 sin b

01 0

sin b 0 cos b

1b 24 C

10 0

0 cos b sin b

0 sin b cos b

7.4 Rotating Shafts on Flexible Supports 411

D. T. Greenwood, 1988, ibid.

FIGURE 7.23

Deﬁnitions of the stiffness constants

representing the stiffness of the

supports.

unbalance angle a  0 and that we can neglect terms with wu, then Eq.

(7.114) becomes

(7.115)

The position vector from the disk center of mass P to the origin of the

inertial reference frame O is given by

(7.116)

After using the ﬁrst row of Eq. (7.115) in Eq. (7.116), we obtain

(7.117)

It is recalled that q(t) is the rotation angle corresponding to the rotation speed

of the shaft. We obtain the velocity of the center of mass P with respect to the

O by taking the time derivative of Eq. (7.117); this leads to

(7.118a)

The z-component of the velocity contains two terms. The ﬁrst term is the ve-

locity of the point C in the axial direction. The second term is the velocity due

to the eccentricity and rotations of the cross section of the shaft. If e is small,

then this second term can be neglected in comparison to the ﬁrst term. This

leads to

(7.118b)

Then, the translational kinetic energy is given by

(7.119)

To determine the rotational kinetic energy, we need to determine the an-

gular speeds about the axis of symmetry ﬁxed in the disk. First, noting that

a  0, we determine the angular speeds about the C-x, C-y, and C-z axes

as follows

(7.120) c

w

cos qcos u  u

sin q

w

sin qcos u  u

cos q

w

sin u 

s 3R

1q 243R

1u 24c

s 3R

1q 24c

s c



m5x

 y

 z

 e

 2eq

3x

sin q  y

cos q46



m1V

 3x

 eq

sin q4i  3y

 eq

cos q4j  z

 3z

 e11q

w  u

2cos q  1q

u  w

2sin q24k

 3x

 eq

sin q4i  3y

 eq

cos q4j

 1x  e cos q2i  1y  e sin q 2j  1z  ew sin q  eu cos q2k

 xi  yj  zk  e3cos qi  sin qj  1w sin q  u cos q2k 4

 R

 R

 xi  yj  zk  ei¿

•

i¿

j¿

k¿

¶ £

cos q sin qwsin q  u cos q

sin q cos qwcos q  u sin q

u w 1

§•

412 CHAPTER 7 Multiple Degree-of-Freedom Systems

where the rotation matrices are given by Eq. (7.113). To determine the angu-

lar speeds of the disk about the principal axes of the disk, we need to rotate

the Cxyz frame through the angle x about the C-y axis. This rotation re-

sults in the angular speeds

(7.121)

If it is assumed that x is a “small” rotation about zero and that the rotation an-

gles w and u are “small” rotations about zero as well, then Eq. (7.121) can be

simpliﬁed to

(7.122)

The rotational kinetic energy T

is obtained from

(7.123)

where J

is the principal inertia of the disk about two of the axes in the plane

of the disk and J

is the principal inertia of the disk about the third axis. Upon

substituting Eq. (7.122) into Eq. (7.123) and performing the matrix multipli-

cations, we obtain

(7.124)

where, by assuming “small” rotational speeds and , the cubic and higher

terms composed of the products of x, u, , and and their squares have been

neglected. However, the terms containing and are not neglected.

Lagrange’s Equations and Equations of Motion

Next, we use Lagrange’s equations to determine the equations governing the

rigid-body motions of the disk. Since there are no potential energy terms and

no damping, the potential energy V  0, and the damping function D  0 in

Eqs. (7.7). To determine the generalized forces, we note that the forces F

, F

and F

are deﬁned along the O-x, O-y, and O-z directions, respectively, and

the moments M

, M

, and M

are deﬁned about the x axis obtained after a w

 2xq

 J

21w

cosq  u

sinq26



 u

 x

2 J

 2w



 v

2 J



0 J

00J

 x3w

cos q  u

sin q  q

 w

 w

sin q  u

cos q

 w

cos q  u

sin q  xq

 c

cos q cos u  u

sin q2cos x  1w

sin u  q

2sin x

w

sin q cos u  u

cos q

cos q cos u  u

sin q2sin x  1w

sin u  q

2cos x

s 3R

1x 24c

s 3R

1x 24c

w

cos qcos u  u

sin q

w

sin qcos u  u

cos q

w

sin u 

7.4 Rotating Shafts on Flexible Supports 413

rotation about the O-x axis, about the intermediate y axis, and C-z axes, re-

spectively. Thus, the forces are Q

 F

, Q

 F

, and Q

 F

, and the mo-

ments are given by

(7.125)

where we have made use of Eq. (7.113) and also assumed a “small” u rotation

about 0. After using the generalized forces and the generalized moments

given by Eq. (7.125) and noting the dependence of T

and T

on the different

variables, the Lagrange equations can be written as

(7.126)

After substituting Eqs. (7.119) and (7.123) into Eq. (7.125) and performing

the indicated operations, we obtain the following equations governing the

translational motions

(7.127a)

(7.127b)

(7.127c)

For the rotational motions, we obtain the governing equations

(7.128a)

(7.128b)

(7.128c)

We can substitute for M

from Eq. (7.128c) into Eq. (7.128a). We note that

in Eq. (7.128a), M

is multiplied by the small angle u. When Eq. (7.128c) is

multiplied by the small angle u, except for the term , all the other terms

can be neglected, since they are higher-order terms. Therefore, Eq. (7.128a)

becomes

(7.129)

If the only external forces acting on the rigid body are those due to the re-

actions of the elastic springs shown in Figure 7.23, then, in general,

(7.130)

and

x  k

u M

x  k

u F

 J

 x1J

 J

21q

cos q  q

sin q2 M

 M

 M

 J

 me

 me1y

cos q  x

sin q2 x1J

 J

21w

cos q  u

sin q2

 J

 x1J

 J

21q

sin q  q

cos q2 M

 J

u  J

 x1J

 J

21q

cos q  q

sin q2 M

 M

 F

 me3q

cos q  q

sin q4 F

 me3q

sin q  q

cos q4 F

b

 F

b

01T

 T

 M

 M

b

 F

b

 M

b

 F

b

 M

 M

s 3R

1u 24

s C

cos u 0 sin u

010

sin u 0 cos u

s c

 M

 M

414 CHAPTER 7 Multiple Degree-of-Freedom Systems

(7.131)

where k

are the spring constants for the coupled motion of the system.

The quantities k

and k

represent the stiffness due to translations only of the

shaft in the x and y directions, respectively, and k

and k

represent the stiff-

ness of the system due to rotations only about the corresponding axes, re-

spectively. The quantities k

, k

, and k

represent the stiffness due to the

coupling of translation and rotation of the shaft. Also, from Maxwell’s recip-

rocal theorem, we have that k

 k

and k

 k

. These spring constants are

determined subsequently.

In view of Eqs. (7.130) and (7.131), Eq. (7.127c) is uncoupled from all

the other equations. In addition, we have already used Eq. (7.128c) to obtain

Eq. (7.129). Thus, there remain four equations that determine the motion of

the system shown in Figure 7.22. After using Eqs. (7.130) and (7.131) in

Eqs. (7.127a), (7.127b), (7.128b), and Eq. (7.129), we arrive at

(7.132)

We now assume that the shaft rotates at constant speed v

; that is, q  v

Then, and , and Eqs. (7.132) become

(7.133a)

(7.133b)

(7.133c)

(7.133d)

The spring constants used in Eqs. (7.133) are determined from a static-

force balance and a static-moment balance. By using a procedure similar to

that shown in Figure 7.5 for “small” u, we ﬁnd that a force balance along the

O-x direction gives

(7.134)

and that a moment balance in the disk plane yields

(7.135)

where a and b are deﬁned in Figure 7.23. If we drop the terms with velocities

and accelerations from Eqs. (7.133a) and (7.133d) and compare the resulting

equations with Eqs. (7.134) and (7.135), respectively, we see that

(7.136)

 a

 b

 k

ak

 bk

 k

 k

 1ak

 bk

2x  1a

 b

 a1x  au2k

 b1x  bu2k

 1k

 k

2x  1ak

 bk

 1x  au 2k

 1x  bu 2k

 J

 k

x  k

u  xv

 J

2cos v

 J

 k

y  k

w xv

 J

2sin v

 k

y  k

w  mev

sin v

 k

x  k

u  mev

cos v

 0q

 v

 J

 k

x  k

u  x1J

 J

21q

sin q  q

cos q2

 J

 k

y  k

w  x1J

 J

21q

cos q  q

sin q2

 k

y  k

w  me3q

cos q  q

sin q4

 k

x  k

u  me3q

sin q  q

cos q4

k

y  k

w M

y  k

w F

7.4 Rotating Shafts on Flexible Supports 415

In a similar manner, we ﬁnd that

(7.137)

We shall restrict ourselves to the symmetrical case where k

 k



 k. Then, from Eqs. (7.136) and (7.137), we obtain

(7.138)

where L is the length of the shaft and

(7.139)

We note that A

 0 when the disk is in the center of the shaft; that is, when

a  b. The quantity k

represents the stiffness due to translation only, k

rep-

resents the stiffness due to rotation only, and k

represents the stiffness due to

the coupling of translation and rotation. When the system is restricted to

translate only, then, k

 k

 0.

In an attempt to identify key parameters that determine the natural fre-

quencies of the system, we introduce the following quantities

(7.140)

After using Eqs. (7.138) and (7.140) in Eqs. (7.133), we obtain the following

nondimensional form of Eqs. (7.133):

(7.141a)

(7.141b)

(7.141c)

(7.141d)

Here, an over dot indicates the derivative with respect to t. The right-hand

side of the ﬁrst two equations contains the force components generated by the

unbalance due to the eccentricity between the center of mass of the disk and

the center of disk that lies on the axis of rotation. The right-hand side of the

last two equations contains rotational inertia components associated with the

angular misalignment of the axis of symmetry of the disk with the axis of ro-

tation of the shaft.

 J



 1A

/2 2X  1A

/2 2u  x

 J

2cos 

 J



 1A

/2 2Y  1A

/2 2w x

 J

2sin 

 Y  1A

/2 2w  e



sin

 X  1A

/2 2u  e



cos



t  v



X  x/L,

Y  y/L,







a  b

and



 b

 k

 kL

 k

 kLA

 k

 2k

 a

 b

 k

ak

 bk

 k

 k

416 CHAPTER 7 Multiple Degree-of-Freedom Systems

Special Cases

Case 1: Translation only When the system only translates in, say, the x di-

rection, then k

 k

 0 and Eq. (7.141a) reduces to Eq. (5.63a) without

damping (i.e., when z  0).

Case 2: Translation and rotation in one plane When the system can both

rotate and translate in only one plane, say the CX-CZ plane and the shaft is

not spinning, then Y  w 

 0 and Eqs. (7.141a) and (7.141d) reduce,

after notational differences are accounted for and damping is omitted, to

Eqs. (b) of Example 7.16.

Case 3: Centrally located mass When the disk is located at the center of the

shaft a  b and, therefore, A

 0. In this case, the Eqs. (7.141a) and (7.141b)

uncouple from each other and from Eqs. (7.141c) and (7.141d). Thus, Eqs.

(7.141a) and (7.141b) become, respectively,

(7.142a)

(7.142b)

Each of Eqs. (7.142) is analogous to the equation obtained for a single

degree-of-freedom system subjected to a rotating unbalanced load given by

Eq. (5.63a) when z  0 in Eq. (5.63a). The solutions to Eqs. (7.142a) and

(7.142b) are, respectively,

(7.143a)

and

(7.143b)

The nondimensional displacement of the center of the disk denoted by r is

given by

(7.144)

which, for a given value of Ω

, is a constant. Thus, the displaced center of the

shaft rotates in a circle of radius r about the point O ﬁxed in the inertial ref-

erence frame. This type of response is known as synchronous whirl. When



 1; that is, when







, then the shaft is said to be rotating at its criti-

cal speed.

General Solution

To obtain an analytical solution to Eqs. (7.140), we introduce the following

complex variables

r  2X

 Y





1 

Y 



1 

sin 

X 



1 

cos 

 Y  e



sin 

 X  e



cos 

7.4 Rotating Shafts on Flexible Supports 417

See Appendix F.

(7.145)

We multiply Eqs. (7.141b) and (7.141c) by j and then add Eqs. (7.141a) and

the modiﬁed (7.141b) together and subtract the modiﬁed Eq. (7.141c) from

Eq. (7.141d) and use Eq. (7.145) to obtain

(7.146)

Free whirling of an undamped system The free whirling of an undamped

system can be obtained by setting in Eq. (7.146) and assuming

that h and j are of the form

(7.147)

where v/v

and v is the vibration frequency. After using Eqs. (7.147)

in Eqs. (7.146), we arrive at

(7.148)

where

4 c

1 

/2 A

/2  J



 J



and

6 e

5Z

6 0

h  h

jt

 ®

jt

 j£

jt

j  j

jt

 X

jt

 jY

jt

 x  0

 jJ



 A

j/2  A

h/2  x1J

 J

2

j

 j  A

h/2  e



j

h  u  jw

j  X  jY

418 CHAPTER 7 Multiple Degree-of-Freedom Systems

a/L  0.1

a/L  0.5

2.5

1.5

0.5

0.5

1

1.5

0 0.5 1



1.5

FIGURE 7.24

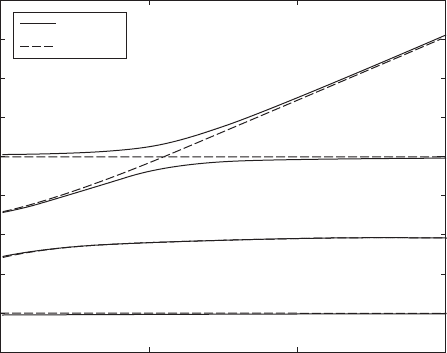
Campbell diagram for a rigid shaft rotating at 

for two different locations of the disk with

 3 and J

 5.

The natural frequencies 

are those values that satisfy ; that is,

when they are the solutions to

(7.149)

After solving numerically

for the four roots of Eq. (7.149) as a function of



, we obtain the results shown in Figure 7.24. This diagram is referred to as

a Campbell diagram. For each value of 

, two of these roots are positive and

the other two are negative. The positive roots correspond to whirling in the

forward direction, and the negative roots correspond to whirling in the reverse

or backward direction.

7.5 STABILITY

Extending the notion of bounded stability presented in Section 4.3, a linear

multi-degree-of-freedom system described by the generalized coordinates x

, . . ., x

and subjected to ﬁnite initial conditions and ﬁnite forcing functions

is said to be stable if

(7.150)

where A has a ﬁnite value. This is a boundedness condition, which requires

the system response {x} to be bounded for bounded system inputs. If this con-

dition is not satisﬁed, then the system is said to be unstable.

EXAMPLE 7.25

Stability of an undamped system with gyroscopic forces

We revisit Examples 7.4 and 7.23 and determine under what conditions the

gyro-sensor is unstable during free oscillations at angular speeds v

. Based on

Eq. (7.150), we need to determine if

(a)

is true. For free oscillations of the gyro-sensor based on the discussion of Sec-

tion 7.3.3, the motion is described by

(b)

where l are the eigenvalues. If one or more of the eigenvalues have a positive

real part, then Eq. (a) will not be true for all time. We can use this as a basis

x1t 2

y1t 2

f e

 y

 A for all time

‘ 5x6‘  2x

 x



 x

 A for all time



 J



 1J

 A

/2 2

 J



A

/2  A

/4  0

0 0

7.5 Stability 419

The MATLAB function roots was used.