Balakumar Balachandran, Magrab E.B. Vibrations
Подождите немного. Документ загружается.

From Eqs. (8.39), it is clear that for a given excitation frequency one can
choose the ratio v
r
and k
32
so that
(8.41)
For this choice of system parameters, then, the displacement of the first iner-
tial element is zero at the excitation frequency that satisfies Eq. (8.41). This
observation is used to design an undamped vibration absorber, which is the
subject of Example 8.3. In general, the excitation frequencies at which the
response amplitude of an inertial element is zero are referred to as the fre-
quencies at which the zeros of the forced response occur for that inertial
element.
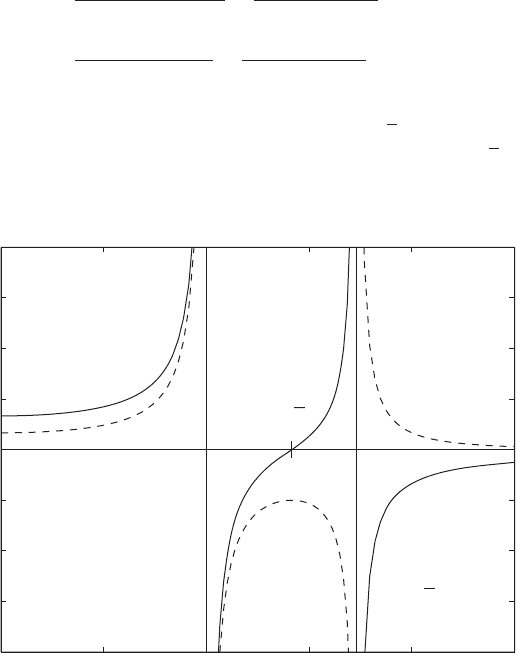
The frequency-response functions given by Eqs. (8.39) are plotted as a
function of the nondimensional excitation frequency for the following pa-
rameter values: m
r
1, v
r
1, and k
32
1. In this case, a
1
4 and a
2
3
and from Eqs. (7.41), (8.38), and (8.39), the frequency-response functions
have the following forms:
(8.42)
Graphs of H
11
() and H
21
() are plotted as functions of in Figure 8.3.
From Eqs. (7.47), it is found that
1
1 and . Thus, it is seen that
H
11
() and H
21
() become infinite-valued for
1
1 and . This is
reflected in Figure 8.3. Furthermore, from this figure it is seen that for
2
13
2
13
H
21
1 2
v
2
r
4
a
1
2
a
2
1
4
4
2
3
H
11
1 2
v
2
r
11 k
32
2
2
4
a
1
2
a
2
2
2
4
4
2
3
2
v
2
r
11 k
32
2
450 CHAPTER 8 Multiple Degree-of-Freedom Systems
0 0.5 1 1.5 2 2.5
4
3
2
1
0
1
2
3
4
Ω
H
i1
(Ω)
Ω
1
1
Ω
2
√3
Ω
√2
FIGURE 8.3
Frequency-response functions of an
undamped two degree-of-freedom
system when harmonic forcing is
applied to mass m
1
. [Solid lines:
H
11
(); dashed lines: H
21
().]

8.2 Normal-Mode Approach 451
, the ratio of H
11
()/H
21
() is positive and that for , this ra-
tio is negative. This is explained in terms of participation of first and second
modes, as discussed in Example 8.5. On examining Figure 8.3, it is clear that
there is a sign change for H
ik
() whenever a resonance location is crossed.
This sign change means that the response phase goes from 0° to 180° or from
180° to 0° as we go from a frequency on one side of a resonance to a fre-
quency on the other side of the resonance.
Undamped Systems: Normal-Mode Approach
In this case, the system of equations given by Eq. (8.33) is uncoupled by mak-
ing use of the transformation given by Eq. (8.2); that is,
(8.43)
where the modal matrix is first determined from the unforced problem
given by Eq. (7.42) and the unknowns to be determined are the modal ampli-
tudes h
1
(t) and h
2
(t). On substituting Eq. (8.43) into Eq. (8.33) and following
the steps used for obtaining Eqs. (8.3) to (8.8), we obtain the following sys-
tem of equations:
(8.44)
In Eq. (8.44), the system natural frequencies v
1
and v
2
are determined
from the eigenvalue problem associated with free oscillations. The modal
masses are determined from Eqs. (7.67) to be
(8.45)
From Eqs. (8.44) and (8.45), it is seen that the system given by Eq. (8.33) has
been transformed into two uncoupled single degree-of-freedom systems, each
of which is treated as in Chapter 5. After solving for the modal amplitudes
h
1
(t) and h
2
(t), one can use Eq. (8.2) to determine the system responses.
Proportionally Damped Systems: Normal-Mode Approach
In this case, the governing equations of motion given by Eq. (7.1b) and for the
forcing described by Eqs. (8.32) take the form
(8.46)
e
F
1
F
2
fcos vt
c
m
1
0
0 m
2
de
x
$
1
x
$
2
f c
c
1
c
2
c
2
c
2
c
2
c
3
de
x
#
1
x
#
2
f c
k
1
k
2
k
2
k
2
k
2
k
3
de
x
1
x
2
f
M
ˆ
22
5X
12
X
22
6
c
m
1
0
0 m
2
de
X
12
X
22
f m
1
X
2
12
m
2
X
2
22
M
ˆ
11
5X
11
X
21
6
c
m
1
0
0 m
2
de
X
11
X
21
f m
1
X
2
11
m
2
X
2
21
M
ˆ
kk
e
1X
11
F
1
X
21
F
2
2/M
ˆ
11
1X
12
F
1
X
22
F
2
2/M
ˆ
22
fcos vt
e
h
$
1
1t 2
h
$
2
1t 2
f c
v
2
1
0
0 v
2
2
de
h
1
1t 2
h
2
1t 2
f c
1/M
ˆ
11
0
01/M
ˆ
22
dc
X
11
X
21
X
12
X
22
de
F
1
F
2
fcos vt
3£ 4
e
x
1
1t 2
x
2
1t 2
f 3£ 4e
h
1
1t 2
h
2
1t 2
f c
X
11
X
12
X
21
X
22
de
h
1
1t 2
h
2
1t 2
f
12
12
where the damping matrix is assumed to have the form of proportional
damping as given by Eq. (7.83); that is,
(8.47)
where a and b are real-valued quantities. Equation (8.47) means that the
damping coefficients need to satisfy the relationships
(8.48a)
from which we find that
(8.48b)
Recall that Eqs. (8.48b) were used in Example 7.21 to determine if the given
system was a proportionally damped system.
To determine the response of the proportionally damped system, we
again uncouple Eq. (8.46) by making use of the transformation given by
Eq. (8.43). Noting that the unknowns to be determined are the modal ampli-
tudes, we substitute Eq. (8.43) into Eq. (8.46) and follow the steps used to ob-
tain Eqs. (8.3) to (8.8) to obtain the following system of equations:
(8.49)
In Eq. (8.49), the system natural frequencies v
1
and v
2
and the system damp-
ing factors z
1
and z
2
are determined from the eigenvalue problem associated
with free oscillations. The modal masses are given by Eqs. (8.45). From
Eqs. (8.46) and (8.49), it is seen that the system of equations given by
Eq. (8.46) has been transformed into two uncoupled single-degree-of-freedom
systems, each of which can be treated as in Chapter 5. After solving for the
modal amplitudes h
1
(t) and h
2
(t), one uses Eq. (8.2) to determine the system re-
sponses. For underdamped systems, the solutions to Eq. (8.49) are given by
Eq. (8.19).
For arbitrarily damped systems, one cannot use the normal-mode ap-
proach to determine the solution for the response. However, one can use either
the state-space formulation discussed in Section 8.3 or the Laplace transform
approach discussed in Section 8.4 to determine the response of a multi-degree-
of-freedom system.
M
ˆ
kk
e
1X
11
F
1
X
21
F
2
2/M
ˆ
11
1X
12
F
1
X
22
F
2
2/M
ˆ
22
fcos vt
c
1/M
ˆ
11
0
01/M
ˆ
22
dc
X
11
X
21
X
12
X
22
de
F
1
F
2
fcos vt
e
h
$
1
1t 2
h
$
2
1t 2
f c
2z
1
v
1
0
02z
2
v
2
de
h
#
1
1t 2
h
#
2
1t 2
f c
v
2
1
0
0 v
2
2
de
h
1
1t 2
h
2
1t 2
f
c
3
am
2
bk
3
c
2
bk
2
c
1
am
1
bk
1
c
2
c
3
am
2
b1k
2
k
3
2
c
2
bk
2
c
1
c
2
am
1
b1k
1
k
2
2
c
c
1
c
2
c
2
c
2
c
2
c
3
d a c
m
1
0
0 m
2
d b c
k
1
k
2
k
2
k
2
k
2
k
3
d
3C 4
452 CHAPTER 8 Multiple Degree-of-Freedom Systems
8.2 Normal-Mode Approach 453
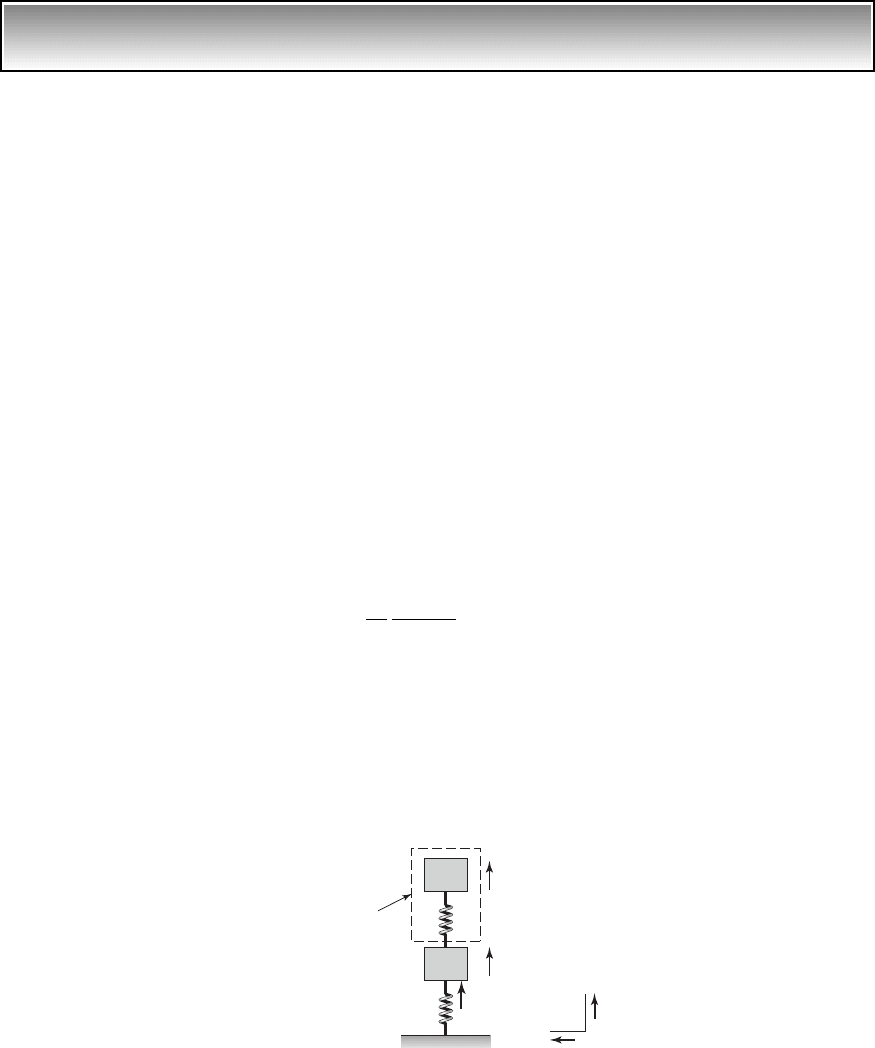
EXAMPLE 8.3 Undamped vibration absorber system
Consider the model of a physical system shown in Figure 7.21 with c
1
0.
This model is an idealization of a primary undamped mechanical system
composed of m
1
and k
1
to which a secondary mechanical system composed of
m
2
and k
2
is attached. The secondary mechanical system is called a vibration
absorber as illustrated in Figure 8.4. The generalized coordinates x
1
and x
2
represent the displacements measured from the static-equilibrium position of
the system.
Single Degree-of-Freedom System
When the secondary system is absent and a harmonic force
(a)
is applied to m
1
, the governing equation of motion is that of a single degree-
of-freedom system given by
(b)
For the harmonically forced single degree-of-freedom system given by
Eq. (b), the resulting forced response is given by Eqs. (5.17) and (5.18) with
z 0. Thus
(c)
It is seen from Eq. (c) that if the excitation frequency is in the vicinity
of the natural frequency v
n1
of the primary system—that is, when 1—
then the resulting response is undesirable. However, if we are required to op-
erate the system at 1 (v v
n1
) or close to it, then a secondary system
can be introduced in order to have a finite amplitude response at the resonance
of the single degree-of-freedom system as illustrated below.
x
1
1t 2
F
1
k
1
sin vt
1
2
m
1
x
$
1
k
1
x
1
F
1
sin vt
f
1
1t 2 F
1
sin vt
k
1
k
2
x
1
(t)
f
1
(t)
x
2
(t)
i
j
m
2
m
1
Secondary system
(absorber)
FIGURE 8.4
Undamped vibration absorber system.

Two Degree-of-Freedom System
The governing equations of the two degree-of-freedom systems are obtained
from Eqs. (7.1a) with c
1
c
2
c
3
k
3
f
2
(t) 0. Thus,
(d)
Assuming a solution of the form,
(e)
and substituting Eq. (e) into Eqs. (d), we obtain Eq. (8.35) with F
2
0. Then
the response amplitudes X
1
and X
2
are obtained from Eqs. (8.39) with k
32
0.
Thus, the forced response is given by
(f)
where upon making use of Eqs. (8.38) and (7.46), we find that
(g)
It is recalled from Eqs. (7.41) that v
r
v
n2
/v
n1
is the ratio of the system’s un-
coupled natural frequencies and v/v
n1
is the excitation frequency ratio.
Since we are forcing the primary system at 1, we see from the first
of Eqs. (f) that X
1
0 when
v
r
1 (h)
or, equivalently, from Eq. (7.41) that
v
n1
v
n2
and v v
n1
(i)
Evaluating D
o
at 1 from Eq. (g) we find that
Then, Eqs. (f) lead to
(j)
Although the harmonic excitation of the primary mass is at a frequency equal
to the primary system’s natural frequency, the choice of the secondary sys-
tem’s parameters are such that v
n1
v
n2
, which makes the response of the
primary system zero. To understand why the response of the primary mass m
1
is zero when the excitation frequency is at the natural frequency of the single
degree-of-freedom system, we consider the free-body diagram shown in Fig-
ure 8.5. In this diagram, the spring forces have been evaluated from Eqs. ( j).
From this figure, it is seen that the spring force generated by the secondary
system, the absorber, is equal and opposite to the excitation force at 1;
X
2
F
1
k
1
1
D
o
F
1
k
1
1k
2
/k
1
2
F
1
k
2
X
1
0
D
o
m
r
v
2
r
k
2
/k
1
.
D
o
4
31 v
2
r
11 m
r
24
2
v
2
r
X
2
F
1
k
1
v
2
r
D
o
X
1
F
1
k
1
v
2
r
2
D
o
e
x
1
1t 2
x
2
1t 2
f e
X
1
X
2
f sin vt
m
2
x
$
2
k
2
x
2
k
2
x
1
0
m
1
x
$
1
1k
1
k
2
2x
1
k
2
x
2
F
1
sin vt
454 CHAPTER 8 Multiple Degree-of-Freedom Systems

that is, the primary mass m
1
does not experience any effective excitation at
1 when the secondary system is designed so that v
r
v
n2
/v
n1
1. If
one considers the two degree-of-freedom system from an input energy-output
energy perspective, all of the energy input to the system at the excitation fre-
quency 1 goes into the secondary system, the absorber. In other words,
the secondary system absorbs all of the input energy.
The natural frequencies of the two degree-of-freedom system are given
by the roots of D
o
0. We find from Eq. (g) that when v
r
1, the natural fre-
quencies are solutions of
(k)
Although the presence of the absorber is good for the system in terms of at-
tenuating the response of the primary mass at v v
n1
, there are still two res-
onances given by the solution to Eq. (k). At these two resonances, the system
response is unbounded since we have an undamped system. This unbounded
response can be eliminated by the inclusion of damping, which is considered
in Section 8.6.
EXAMPLE 8.4
Absorber for a diesel engine
2
An engine of mass 300 kg is found to experience undesirable vibrations at an
operating speed of 6000 rpm. If the magnitude of the excitation force is
240 N, design a vibration absorber for this system so that the maximum am-
plitude of the absorber mass does not exceed 3 mm.
To design the vibration absorber for this system, we make use of the
analysis of Example 8.3 and the parameters given above to determine the ab-
sorber stiffness k
2
and the absorber mass m
2
. From the information provided,
the excitation frequency is given by
rad/s (a)v
12p rad/rev 216000 rev/min2
60 s/min
628.32
4
12 m
r
2
2
1 0
8.2 Normal-Mode Approach 455
F
1
sin
n1
t k
2
(X
1
X
2
) sin
n1
t F
1
sin
n1
t
k
1
X
1
sin
n1
t 0
m
1
FIGURE 8.5
Free-body diagram of mass m
1
for v
r
1 and 1.
2
S. S. Rao, Mechanical Vibrations, Addison-Wesley, Reading, MA, Chapter 9 (1995).

and the excitation amplitude is
(b)
The amplitude X
2
of the absorber mass has to be such that
(c)
It is assumed that the system is operating at the natural frequency of the
engine—that is, v v
n1
—and that the absorber is designed so that v
n1
v
n2
(the absorber’s natural frequency is the same as the engine’s natural fre-
quency). From Eq. (a) and Eqs. (7.41), we arrive at
(d)
Equation (d) provides us one of the equations needed to determine the pa-
rameters k
2
and m
2
of the absorber. To determine another equation, we make
use of Eq. (b) and Eq. ( j) from Example 8.3 to arrive at
(e)
From Eqs. (c) and (e), we find that the absorber stiffness should be such that
or
(f)
Making use of Eq. (d), we determine the absorber mass to be
(g)
Choosing k
2
100 10
3
N/m so that Eq. (f) is satisfied leads to m
2
0.253 kg.
EXAMPLE 8.5
Forced response of a system with bounce and pitch motions
We build on Example 7.16 and construct the frequency-response functions
and then graph them. Since the system is undamped, we can use the direct ap-
proach presented in Section 8.2.3. Based on Eqs. (a) and (b) of Example 7.16
and Eq. (8.34), we obtain the following set of equations when the harmonic
forcing of amplitude F
1
is applied to the center of gravity of the system; that
is, point G in Figure 7.5.
(a)11 k
21
L
21
2Y a
2
k
21
L
2
21
v
2
r
1 k
21
L
2
21
bX 0
1
2
1 k
21
2Y 11 k
21
L
21
2X F
1
/k
1
m
2
k
2
1628.32 2
2
k
2
80 10
3
N/m
0X
2
0
F
1
k
2
240
k
2
0.003 m
0X
2
0
F
1
k
2
240
k
2
v
2
n2
k
2
m
2
v
2
n1
v
2
1628.322
2
rad
2
/s
2
0X
2
0 3 10
3
m
F
1
240 N
456 CHAPTER 8 Multiple Degree-of-Freedom Systems
where X L
1
. Upon solving Eqs. (a) for the forced response amplitudes, we
obtain
(b)
where the term has the form
(c)
The coefficients b
j
in Eqs. (c) are given in Eqs. (d) of Example 7.16. The
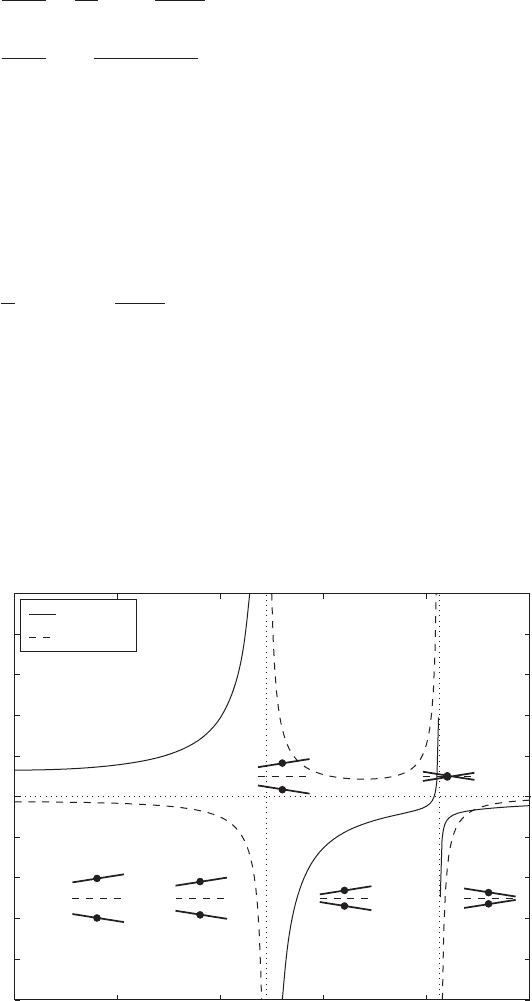
frequency-response functions given by Eqs. (b) are plotted in Figure 8.6 for
the parameters used in Example 7.16. We see that the relative motion of the
beam at different frequencies is
(d)
provided that k
21
L
21
1 and that is, when
j
. When —
that is, when
j
—the responses are unbounded and the solution given
by Eq. (8.34) is not valid.
Equation (d) is used to plot the relative motion of the beam at frequen-
cies other than those at
j
in Figure 8.6. From this figure, it is seen that the
displacement amplitude Y and the rotation of the bar in Figure 8.6 become
unbounded when the excitation frequency is equal to either one of the natural
frequencies; that is, when v v
j
(
j
). When the excitation frequency is
D¿
o
0D¿
o
0;
Y
X
a
2
k
21
L
2
21
v
2
r
1 k
21
L
2
21
b/11 k
21
L
21
2
D¿
o
b
1
4
b
2
2
b
3
D¿
o
X
F
1
/k
1
11 k
21
L
21
2
D¿
o
Y
F
1
/k
1
1
D¿
o
a
2
k
21
L
2
21
v
2
r
1 k
21
L
2
21
b
8.2 Normal-Mode Approach 457
0 0.5 1 1.5 2 2.5
5
4
3
2
1
0
1
2
3
4
5
Amplitude
Ω
Ω
1
1.22
Ω
2
2.06
Ω
0.4
Ω
1.6
Ω
1.22
Ω
2.06
Ω
2.3
Ω
0.9
Y/(F
1
/k
1
)
X/(F
1
/k
1
)
FIGURE 8.6
Amplitudes of frequency-response
functions for the system in Figure 7.5
and the envelopes of motion of the
bar at selected frequencies. The
solid dot shown on the envelopes is
the point G in Figure 7.5.

below the first natural frequency (
1
), it is clear from the displacement
pattern and the discussion of Example 7.16 that the first mode dominates the
response. On the other hand, when the excitation frequency is above the sec-
ond natural frequency (
2
), it is clear from the displacement pattern that
the second mode dominates the response. In the intermediate response region,
1
2
, neither the first nor the second mode is dominant.
8.3 STATE-SPACE FORMULATION
In Section 8.2, we discussed how the response of a damped system can be de-
termined for proportionally damped systems. In this section, we discuss how
the response of a multi-degree-of-freedom system can be determined for a
system with an arbitrary damping matrix.
The approach is based on a standard solution procedure from the theory
of ordinary differential equations, where the governing equations are rewrit-
ten as a set of first-order equations called the state-space form. Although one
can obtain this form for both linear and nonlinear systems, here, we restrict our
discussion to linear multi-degree-of-freedom systems. To this end, we start
with the governing equations given by Eq. (7.3) for a system with damping,
circulatory forces, and gyroscopic forces. These equations are repeated below
after replacing the force vector {Q} on the right-hand side by {F}. Thus,
(8.50)
where
(8.51)
We now introduce the new vectors {Y
1
} and {Y
2
}, which are defined as
(8.52)
From Eqs. (8.52), it is clear that {Y
1
} is the displacement vector containing
the N displacements q
i
and {Y
2
} is the velocity vector containing the N
and
5Y
#
2
6 5q
$
6 µ
q
$
1
q
$
2
o
q
$
N
∂
5Y
1
6 5q6 µ
q
1
q
2
o
q
N
∂,
5Y
2
6 5Y
#
1
6 5q
#
6 µ
q
#
1
q
#
2
o
q
#
N
∂,
5q
$
6 µ
q
$
1
q
$
2
o
q
$
N
∂,
5q
#
6 µ
q
#
1
q
#
2
o
q
#
N
∂,
5q6 µ
q
1
q
2
o
q
N
∂,
and
5F6 µ
f
1
1t 2
f
2
1t 2
o
f
N
1t 2
∂
3M 45q
$
6 33C4 3G 445q
#
6 33K4 3H 445q6 5F6
458 CHAPTER 8 Multiple Degree-of-Freedom Systems
velocities . On substituting Eqs. (8.52) into Eq. (8.50), we arrive at the fol-
lowing system of N first-order equations
(8.53)
From Eqs. (8.52), we have the second set of N first-order equations
(8.54)
where is an NN identity matrix given by
Equation (8.53) is written as
(8.55a)
or
(8.55b)
provided that the inverse of the inertia matrix exists. Upon combining
the two sets of first-order differential equations given by Eqs. (8.54) and
(8.55b), we arrive at the following system of 2N first-order differential
equations
(8.56)
where the (2N1) state vector {Y} and its time derivative are given by
(8.57)
In Eq. (8.56), the (2N2N) state matrix and the (2NN ) matrix are,
respectively, given by
(8.58) 3B 4 e
30 4
3M 4
1
f
3A 4 c
30 43I4
3M4
1
33K 4 3H44 3M4
1
33C 4 3G44
d
3B 43A 4
5Y6 e
Y
1
Y
2
f h
q
1
q
2
o
q
N
q
#
1
q
#
2
o
q
#
N
x
and
5Y
#
6 e
Y
#
1
Y
#
2
f h
q
#
1
q
#
2
o
q
#
N
q
$
1
q
$
2
o
q
$
N
x
5Y
#
6
5Y
#
6 3A45Y6 3B 45F6
3M 4
1
3H445Y
1
6 3M4
1
5F6
5Y
#
2
63M4
1
33C 4 3G445Y
2
6 3M4
1
33K 4
3M 4
1
5F6
5Y
#
2
6 3M4
1
33C 4 3G445Y
2
6 3M4
1
33K 4 3H445Y
1
6
3I 4 ≥
10
p
0
01
p
0
oo∞o
00
p
1
¥
3I 4
5Y
#
1
6 3I45Y
2
6
3M 45Y
#
2
6 33C4 3G 445Y
2
6 33K4 3H 445Y
1
6 5F6
q
#
i
8.3 State-Space Formulation 459
