Balakumar Balachandran, Magrab E.B. Vibrations
Подождите немного. Документ загружается.

to determine the angular speeds v
z
for which the system will be either unsta-
ble or stable.
For the special case treated in Example 7.23, the eigenvalues are given by
Eqs. (g). From these eigenvalues, we arrive at the following angular speed
range for instability
(c)
which is not possible.
EXAMPLE 7.26
Wind-induced vibrations of a suspension bridge deck:
stability analysis
38
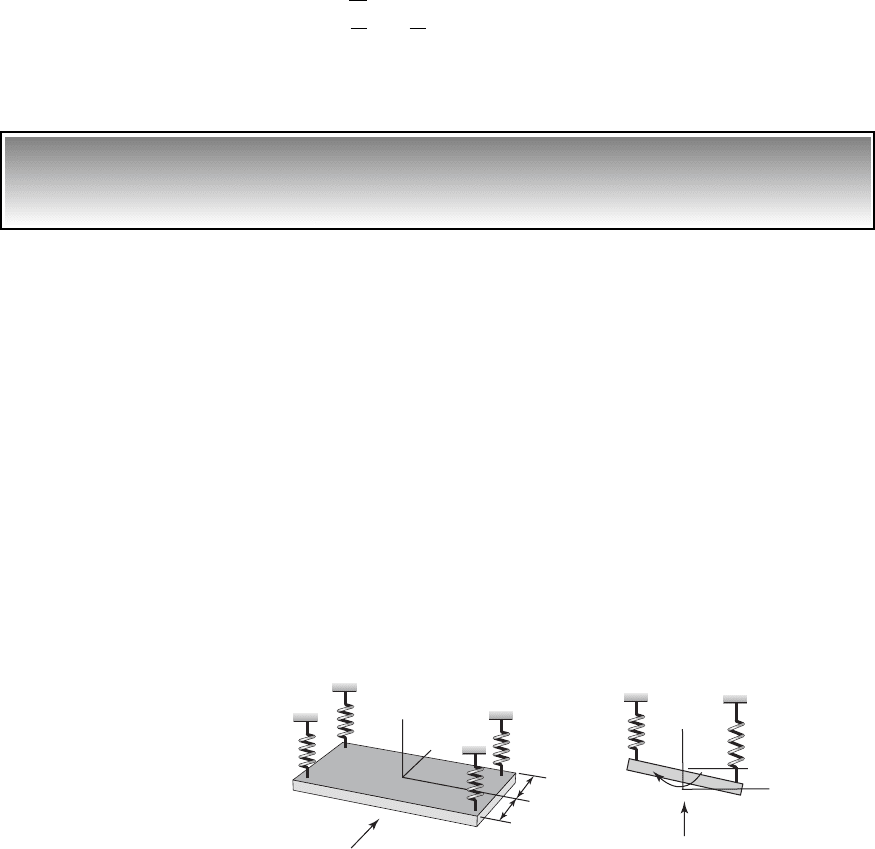
Consider a section of a deck of a suspension bridge that is subjected to a wind
with a speed V. Let us assume that a section of the deck can be modeled as
shown in Figure 7.25, where the linear springs are specified in terms of stiff-
ness per unit length of the deck. The wind produces a lifting force F in the ver-
tical direction and a moment M, as shown in the figure. The vertical motion
of the deck is independent of the torsional motion. If the deck has a mass per
unit length m and a mass moment of inertia J about the longitudinal axis of
the deck, then the governing equations of motion in the vertical and torsional
directions are, respectively,
(a)
where we have used Eq. (k) of Example 7.3 with k
1
k
2
K/2 and L
1
L
2
L. Through this example, we shall illustrate how to carry out a stability
analysis for a system with two degrees of freedom.
Ju
$
KL
2
u M
my
$
Ky F
2v
z
B
k
m
a
k
m
v
2
z
b
420 CHAPTER 7 Multiple Degree-of-Freedom Systems
38
M. Roseau, Vibrations in Mechanical Systems: Analytical Methods and Applications, Springer-
Verlag, Berlin, Germany, 1983, pp. 236–243.
K/2
K/2
K/2
K/2
L
L
y
x
z
V
O
y
x
K/2
K/2
F
M
O
FIGURE 7.25
Model of a bridge deck subjected to a wind with a speed V.
Under some simplifying assumptions, the wind-induced lifting force and
moment can be expressed as
(b)
where c
F
and c
M
are constants and r is the density of air. Upon substituting
Eqs. (b) into Eqs. (a), we obtain the coupled equations
(c)
Next, we introduce the following quantities
into Eqs. (c) and obtain
(d)
where the over dot now indicates the derivative with respect to t.
To investigate the stability of the system, we assume a solution of the form
(e)
We substitute Eqs. (e) into Eqs. (d) to obtain
(f)
Setting the determinant of the coefficients in Eq. (f) to zero, we obtain the fol-
lowing fourth-order polynomial in l
(g)
1
2
y
M
M
2
u
M
F
2l
2
y
1
2
u
M
M
2 0
l
4
1M
F
M
M
2l
3
1
2
y
2
u
M
M
M
F
M
M
2l
2
c
l
2
M
F
l
2
y
M
F
M
M
ll
2
M
M
l
2
u
M
M
de
W
o
®
o
f e
0
0
f
u1t 2 ®
o
e
lt
w1t 2 W
o
e
lt
u
$
M
M
u
#
1
2
u
M
M
2u M
M
w
#
0
w
$
M
F
w
#
2
y
w M
F
u 0
2
y
v
2
y
v
2
o
,
2
u
v
2
u
v
2
o
M
F
c
F
rL
2
m
,
M
M
c
M
rL
4
J
,
t v
o
t
w
y
L
,
v
o
V
L
,
v
2
y
K
m
,
v
2
u
KL
2
J
Ju
$
KL
2
u c
M
rL
2
V
2
cau
y
#
V
b
L
V
u
#
d
my
$
Ky c
F
rLV
2
au
y
#
V
b
M c
M
rL
2
V
2
cau
y
#
V
b
L
V
u
#
d
F c
F
rLV
2
au
y
#
V
b
7.5 Stability 421

The stability conditions for this system are determined by examining cer-
tain combinations of the coefficients of this polynomial using the Routh-
Hurwitz stability criterion.
39
7.6
SUMMARY
In this chapter, the derivation of the governing equations of a multi-degree-
of-freedom system was illustrated by making use of force-balance and
moment-balance methods and Lagrange’s equations. Linearization of the
equations governing a nonlinear system was also addressed. Means to deter-
mine the natural frequencies and mode shapes were introduced, and the no-
tions of orthogonality of modes, modal mass, modal stiffness, proportional
damping, modal damping factor, node of a mode, and rigid-body mode were
introduced. The conditions under which conservation of energy, conservation
of linear momentum, and conservation of angular momentum hold during
free-oscillations of a multiple degree-of-freedom system were determined.
Finally, the notion of stability of a linear multi-degree-of-freedom system was
introduced.
422 CHAPTER 7 Multiple Degree-of-Freedom Systems
39
The polynomial given by Eq. (g) is of the form
where b
j
0, j 1, 2, 3, 4. For none of the roots of the polynomial to have positive real parts,
the following criteria must be satisfied
b
1
0,
2
b
1
1
b
3
b
2
2 0,
3
b
1
10
b
3
b
2
b
1
0 b
4
b
3
3 0,
and
4
b
1
100
b
3
b
2
b
1
1
0 b
4
b
3
b
2
000b
4
4 0
l
4
b
1
l
3
b
2
l
2
b
3
l b
4
0
EXERCISES
Section 7.2.1
7.1 Consider the “small” amplitude motions of the
pendulum-absorber system shown in Figure 7.9 and
derive the equations of motion by using force-balance
and moment-balance methods.
7.2 Derive the equations of the hand-arm system
treated in Example 7.11 by using force-balance and
moment-balance methods for “large” and “small” os-
cillations about the nominal position.
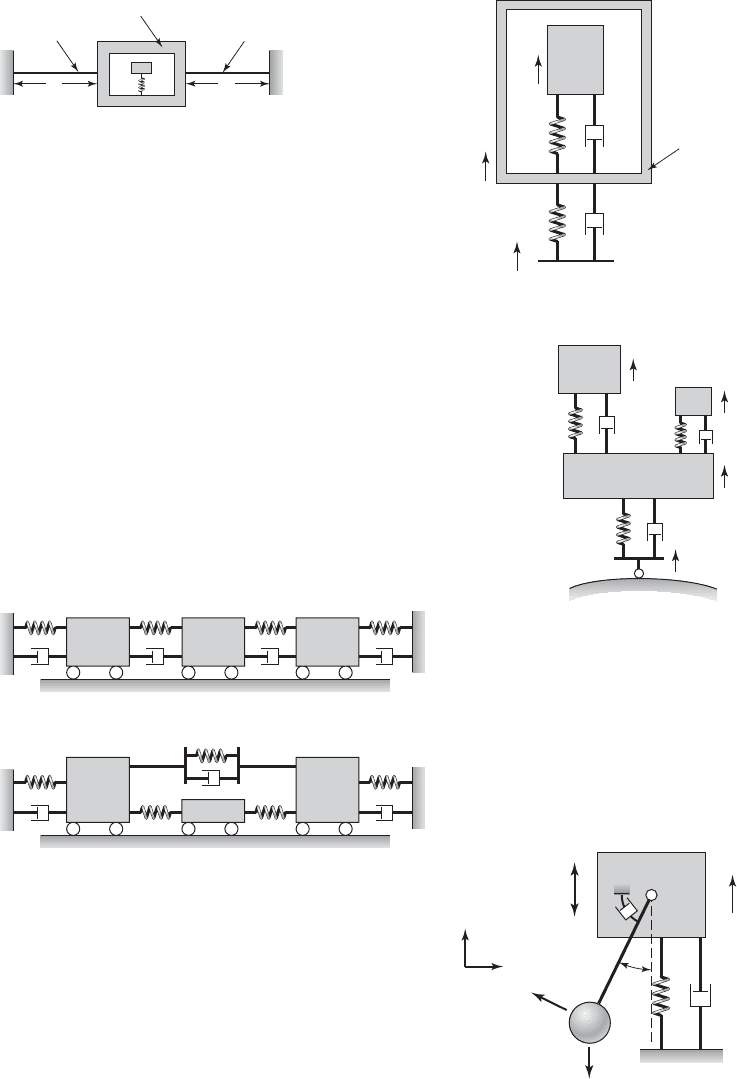
7.3 A container of mass m
c
is suspended by two taut
cables of length L as shown in Figure E7.3. The ten-
sion in the cables is T
o
. Inside the container, a mass m
is elastically supported by a spring k.
a) Determine the equivalent spring constant for the
cable-mass system and sketch the equivalent vi-
bratory system.
b) For the equivalent system determined in part (a),
determine the equations governing the motion of
this system.
7.4 A two degree-of-freedom system with a nonlinear
spring element is described by the following system
of equations:
Determine the system equilibrium positions. Assume
that m
1
, m
2
, k
1
, and k
2
are positive and a is negative.
Section 7.2.3
7.5 Derive the equations of motion of the systems
shown in Figures E7.5a and E7.5b and present the
resulting equations in each case in matrix form.
m
2
x
$
2
k
2
1x
2
x
1
2 k
2
a1x
2
x
1
2
3
0
k
2
a1x
1
x
2
2
3
0
m
1
x
$
1
k
1
x
1
ax
3
1
k
2
1x
1
x
2
2
Exercises 423
Cable
Cable
L L
m
k
m
c
FIGURE E7.3
7.8 Derive the equations of motion of the pendulum
absorber shown in Figure E7.8 for large oscillations
and then linearize these equations about the static-
equilibrium position corresponding to the bottom po-
sition of the pendulum. Present the final equations in
matrix form.
FIGURE E7.5
FIGURE E7.7
FIGURE E7.8
FIGURE E7.6
7.6 Derive the equations of motion for the model of
an electronic system m
2
contained in a package m
1
,
as shown in Figure E7.6, and present them in matrix
form.
7.7 Derive the equations of motion of the vehicle
model shown in Figure E7.7.
k
1
x
3
x
1
(t)
x
2
(t)
c
1
k
2
c
2
m
2
m
1
y
1
y
3
y
2
y
e
c
3
c
1
c
2
k
3
k
1
k
2
m
1
m
3
m
2
Automobile
body
Suspension
Axle and
wheel mass
Tire stiffness
and damping
Absorber
x
M
l
c
mg
k
c
t
l
j
i
.
F
o
cos t
m
k
4
c
4
k
3
c
3
k
2
c
2
k
1
c
1
m
1
m
2
m
3
c
4
k
4
k
5
c
5
k
3
k
2
k
1
c
1
m
1
m
2
m
3
(a)
(b)

7.9 Derive the equations of motion of the system
shown in Figure E7.9 by using Lagrange’s equations.
424 CHAPTER 7 Multiple Degree-of-Freedom Systems
7.13
The experimental arrangement for an airfoil
mounted in a wind tunnel is described by the model
shown in Figure E7.13. Determine the equations of
motion governing this system when the stiffness of
the translation spring is k, the stiffness of the torsion
spring is k
t
, G is the center of the mass of the airfoil
located a distance l from the attachment point O,
m is the mass of the airfoil, and J
G
is the mass moment
of inertia of the airfoil about the center of mass. Use
the generalized coordinates x and u discussed in
Exercise 1.13.
FIGURE E7.9
FIGURE E7.12
FIGURE E7.13
FIGURE E7.14
7.10 Replace each of the linear springs k
2
and k
3
shown in Figure E7.9 by a nonlinear spring whose
force-displacement characteristic is given by
and determine the resulting equations of motion.
7.11 Derive the equations of the milling model shown
in Figure 7.4b by using Lagrange’s equations.
7.12 Derive the equations of motion of the system
shown in Figure E7.12, which is an extended version
of a two degree-of-freedom system discussed in Sec-
tion 7.2. Let M
o
(t) be the external torque that acts on
the disc whose motion is described by the angular
variable w
1
.
F1x 2 k1x ax
3
2
l
m, J
G
G
k
O'
O
k
t
7.14 A multistory building is described by the model
shown in Figure E7.14. Derive the equations of mo-
tion of this system and present them in matrix form.
Are the mass and stiffness matrices symmetric?
x
4
x
3
x
2
x
1
k
4
k
4
k
3
k
3
k
2
k
2
k
1
k
1
m
4
m
3
j
i
m
2
m
1
x
1
x
2
k
2
k
3
k
4
k
1
c
1
c
2
m
1
m
2
k
t1
k
t2
1
2
3
c
t2
c
t3
c
t1
J
o1
J
o2
J
o3
M
o
(t)
Oil housing
k
t3
k
7.15 Obtain the governing equations of motion for
large oscillations of the system shown in Figure E7.15
in terms of the generalized coordinates x
1
, x
2
, and u.
The spring k
3
is attached at the midpoint of the bar.
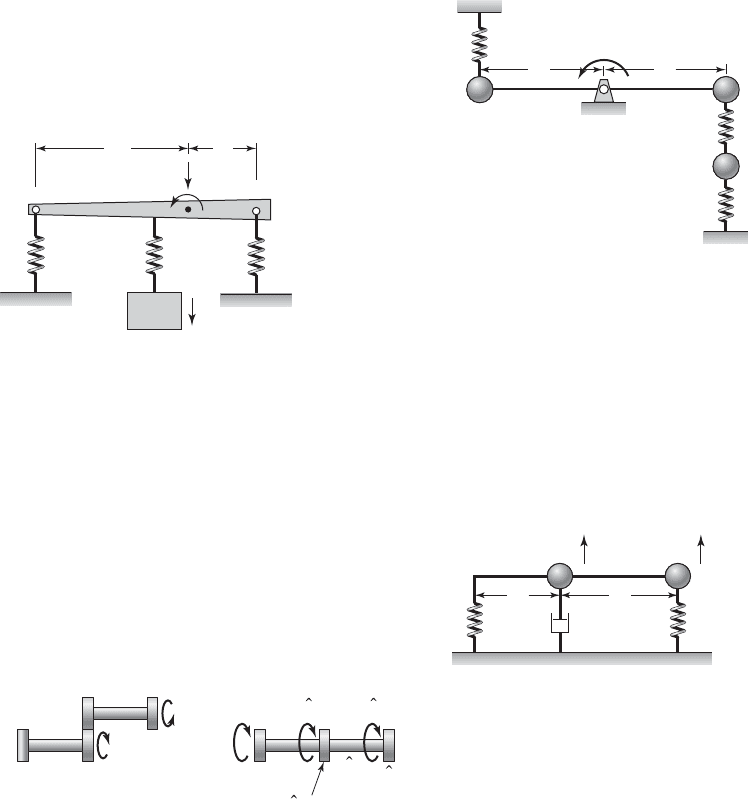
Linearize the resulting system of equations for
“small” motions about the system equilibrium posi-
tion and present the resulting equations in matrix
form. Point G is the center of mass of the bar.
Exercises 425
7.18
Consider the vibratory system shown in Figure
E7.18, which consists of two masses that are con-
nected by rigid massless rods. Determine the equa-
tions of motion of the system. Assume that gravity
acts normal to the plane of the system.
k
2
k
3
x
1
x
2
k
1
L
1
L
2
G
m
1
, J
G
m
2
FIGURE E7.15
FIGURE E7.17
FIGURE E7.18
FIGURE E7.16
7.16 A pair of shafts are linked by a set of gears as
shown in Figure E7.16a. An equivalent system for
the system shown in Figure E7.16a is determined as
shown in Figure E7.16b, where
and the transmission ratio T
R
v
out
/v
in
. Determine
the governing equations of motion of the system
shown in Figure E7.16b in terms of the generalized
coordinates where f
ˆ
i
f
i
/T
R
.f
1
, f
ˆ
2
, and f
ˆ
4
J
ˆ
i
J
i
T
2
R
, k
ˆ
t2
k
t2
T
2
R
m
1
mm
k
1
LL
O
k
2
k
3
T(t)
7.19 Consider the vibratory system shown in Fig-
ure E7.19.
a) If the connecting rod is rigid and uniform with
a total mass m, then determine the equations of
motion for the system.
b) If the connecting rod is rigid and weightless, then
determine the equations of motion for the system.
c) If the connecting rod is rigid and weightless and
the pivot is removed; that is, the rod can translate
vertically and rotate in the plane of the page,
then determine the equations of motion for the
system.
J
3
J
4
J
4
k
t2
k
t2
k
t1
k
t1
J
2
J
1
J
1
J
3
+ J
2
in
out
1
2
4
(b)(a)
7.17 As shown in Figure E7.17, a rigid weightless rod
of length 2L is attached to a pivot at its center. At each
end of the rod, a mass m is attached. Assume “small”
rotations and that gravity acts normal to the plane of
the system. To one of the end masses another spring-
mass system is attached. A torque T(t) is applied to
the rod at the pivot as shown in the figure. Obtain the
equations of motion for this system.
y
2
m
2
m
1
y
1
k
1
L
1
L
2
k
2
c
1
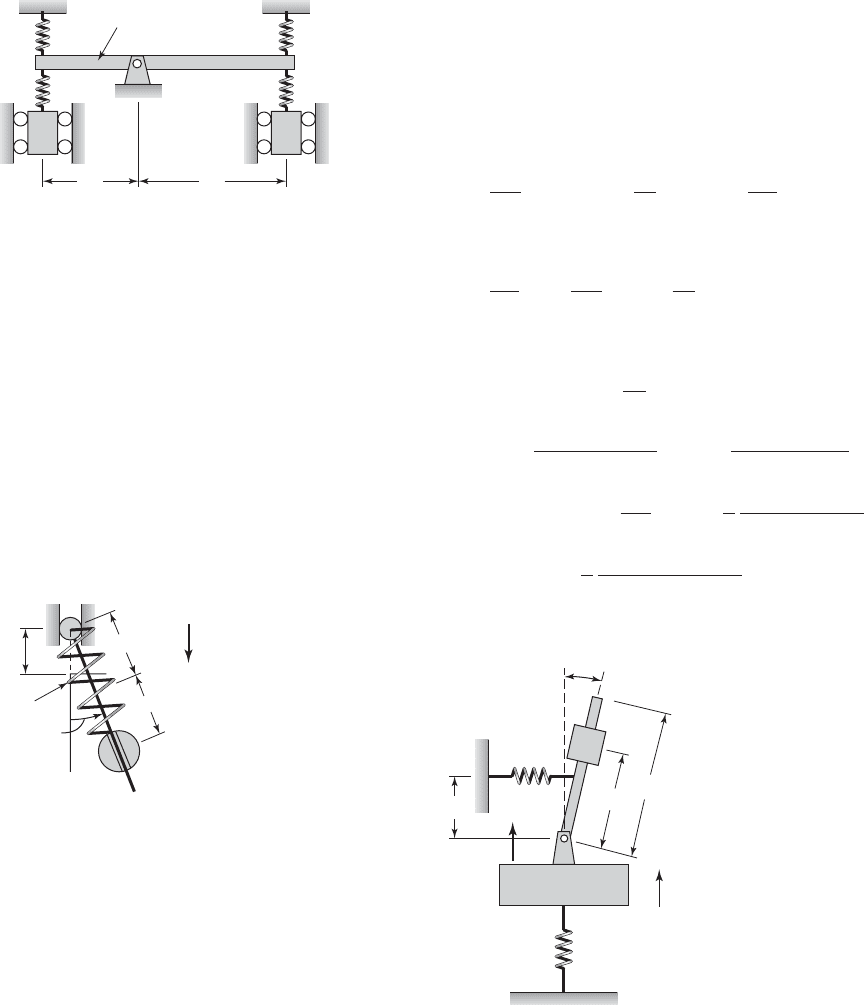
7.20 The mass m shown in Figure E.7.20 slides in a
gravity field along a massless rod. Wrapped around the
rod is a massless spring of constant k that has an un-
stretched length L. One end of the rod is attached to a
vertically moving pivot that oscillates harmonically as
The position of the mass along the rod is u(t), which
is measured from the unstretched position of the
spring. Use Lagrange’s equations to obtain the non-
linear equations of motion.
z1t 2 z
o
cos vt
426 CHAPTER 7 Multiple Degree-of-Freedom Systems
Attached to the rod at a distance l
s
from the pivot is a
spring k
2
.
a) Determine expressions for the kinetic energy and
the potential energy of the system.
b) Show that the nonlinear equations of motions for
this system are
where
and
g
2
1
2
l
2
2
1m
2
2m
3
l
3
/l
2
2
m
2
l
2
2
/3 m
3
l
2
3
X x/l
2
,
F
o
f
o
k
1
l
2
,
g
1
1
2
m
2
2m
3
l
3
/l
2
m
1
m
2
m
3
,
v
2
1
k
1
m
1
m
2
m
3
,
v
2
2
k
2
l
2
s
m
2
l
2
2
/3 m
3
l
2
3
t v
1
t,
v
v
1
,
d
2
u
dt
2
g
2
d
2
X
dt
2
sinu
v
2
2
v
2
1
sinu cosu 0
F
o
cos t
d
2
X
dt
2
X g
1
ca
du
dt
b
2
cosu
d
2
u
dt
2
sinu d
k
1
k
3
k
2
L
1
O
L
2
k
4
m
1
m
2
m
FIGURE E7.19
FIGURE E7.20
FIGURE E7.21
u(t)
L
z
(t)
(t)
k
x
y
g
m
7.21 Consider the autoparametric vibration absorber
shown in Figure E7.21. The system composed of mass
m
1
and spring k
1
is externally excited by a harmoni-
cally oscillating force
The oscillations of this primary system are to be at-
tenuated by attaching another system composed of a
mass m
3
that is attached to a rigid rod of mass m
2
and
length l
2
. The base of the rod is pivoted on mass m
1
.
f 1t 2 f
o
cos vt
l
3
k
1
k
2
m
2
l
s
l
2
x(t)
f(t)
m
3
m
1
(t)
7.22 Consider the pulley-cable-mass system shown in
Figure E7.22. Use Lagrange’s equations to determine
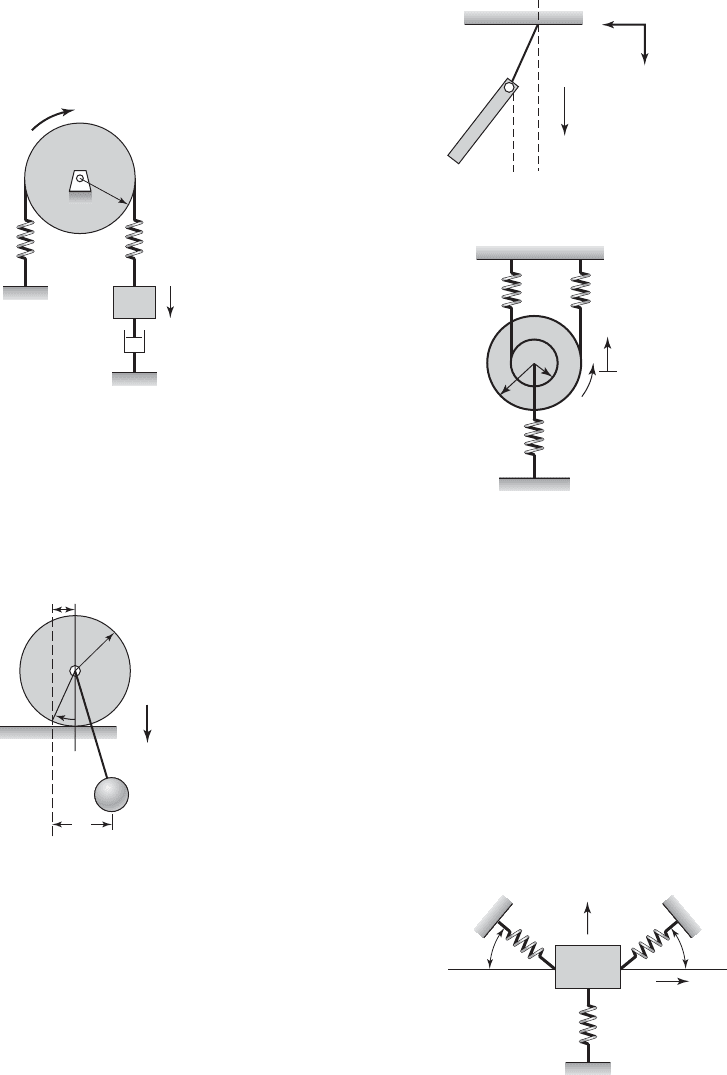
the equation of motion of this system and place these
equations in matrix form.
Exercises 427
7.23
For the system shown in Figure E7.23, determine
the equations of motion. Assume that the length of the
pendulum is L.
about the static-equilibrium position. Compare your
results to those obtained for “small” oscillations in
Example 7.3 after setting the damping coefficients c
1
and c
2
to zero.
Section 7.3.1
7.26 Determine the natural frequencies and mode
shapes for the system shown in Figure E7.26, when
u
1
30°and u
2
45°at the equilibrium position. Let
L be the length of each spring at the equilibrium
position and assume that the deflections in the springs
at an angle are small.
FIGURE E7.22
FIGURE E7.23
FIGURE E7.24
k
2
k
1
m
J
r
c
2
x
M(t),
FIGURE E7.25
x
1
x
2
r
g
m
2
m
1
L
1
L
2
1
2
g
m
O
i
j
k
2
k
3
k
1
m, j
o
y
R
O
r
7.24 Consider the system that is shown in Figure
E7.24, where a uniform rod of length L
2
and mass m
is suspended from a massless rod of length L
1
. The rod
of length L
1
is connected to the rod of length L
2
by a
frictionless hinge. Determine the equations of motion.
7.25 Derive the governing equations of the friction-
less system shown in Figure E7.25. Assume motions
k
kk
y
x
1
2
m
FIGURE E7.26
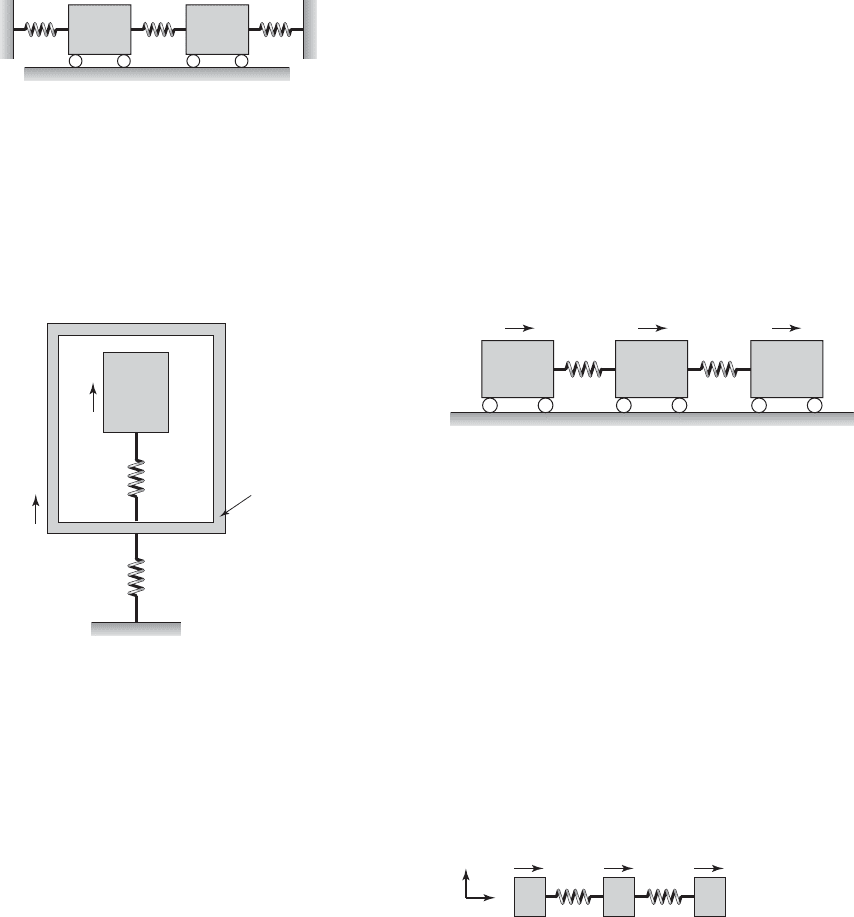
7.27 Determine the natural frequencies and mode
shapes associated with the system shown in Fig-
ure E7.27 for m
1
10 kg, m
2
20 kg, k
1
100 N/m,
k
2
100 N/m, and k
3
50 N/m.
428 CHAPTER 7 Multiple Degree-of-Freedom Systems
7.30
Consider a system with the following inertia and
stiffness matrices:
N/m
If the modes of the system are given by
and the natural frequency associated with {X}
1
is
19.55 rad/s, then determine the unknown coefficients
in the stiffness matrix and the other natural frequency
of the system.
7.31 Determine if the system shown in Figure E7.31
has any rigid-body modes.
5X6
1
e
0.5414
1
f
and
5X6
2
e
5.5575
1
f
3M 4 c
20
06
d kg;
3K 4 c
10,000 k
kk
22
d
FIGURE E7.27
FIGURE E7.28
FIGURE E7.31
FIGURE E7.33
k
1
k
2
k
3
m
1
m
2
k
1
y
1
(t)
y
2
(t)
k
2
m
1
m
2
k
1
x
1
x
2
x
3
k
3
m
1
m
2
m
3
x
3
x
2
x
1
kk
m 2mm
j
i
7.28 Determine the natural frequencies and mode
shapes associated with the system shown in Fig-
ure E7.28 for m
1
10
3
kg, m
2
0.01 kg, and k
1
k
2
2 kN/m. Include plots of the mode shapes.
7.29 For the system considered in Exercise 7.10, re-
move the nonlinear spring k
3
by considering small
displacements about x
o
, set the damping coefficients
c
1
c
4
0, and consider the free oscillations of this
system. Choose the values of the parameters as fol-
lows: m
1
10 kg, m
2
2 kg, k
1
k
4
k 10 N/m,
and a 2 m
2
. Assume that the nonlinear spring is
initially compressed by x
o
0.05 m. Determine the
natural frequencies and mode shapes associated with
free oscillations about the equilibrium position.
7.32 Let the system shown in Figure E7.31 represent
a system of three railroad cars with masses m
1
m
2
m
3
1200 kg and interconnections k
1
k
3
4800 kN/m. Determine the natural frequencies and
mode shapes of this system and plot the correspon-
ding mode shapes.
7.33 A flexible structural system is represented by
the model shown in Figure E7.33. Determine the gov-
erning equations of motion of this system, and from
these three equations, determine the eigenvalues and
eigenvectors associated with free oscillations of this
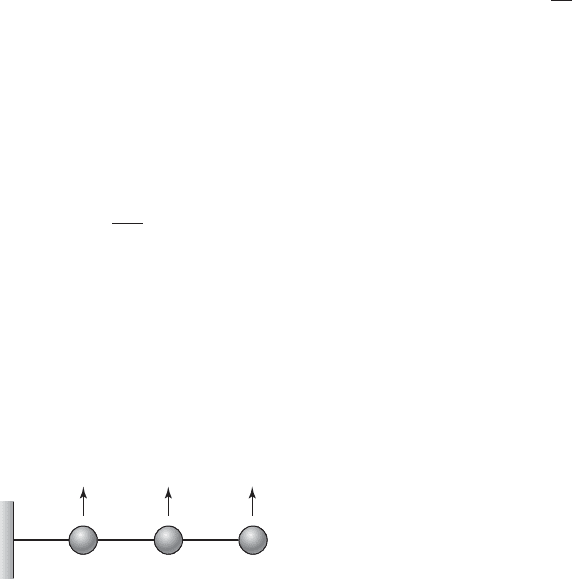
system. Find the locations of the nodes for the differ-
ent mode shapes.
7.34 Consider the system shown in Figure E7.34 in
which the three masses m
1
, m
2
, and m
3
are located on
a uniform cantilever beam with flexural rigidity
EI. The inverse of the stiffness matrix for this
system , which is called the flexibility matrix, is
given by
Determine the following: (a) the stiffness matrix of
the system, (b) the governing equations of motion,
and (c) when m
1
m
2
m
3
m, determine the nat-
ural frequencies and mode shapes of the system. For
part (c), let a 3EI/mL
3
and express the natural fre-
quencies in terms of a.
3K 4
1
L
3
3EI
C
27 14 4
14 8 2.5
4 2.5 1
S
3K 4
Exercises 429
If all the masses of the floors of the four-story build-
ing are equal; that is, m
1
m
2
m
3
m
4
m, then
determine the system eigenvalues and eigenvectors
and plot the eigenvectors of this system. Let a
EI/mL
3
and express the natural frequencies in terms
of a.
7.36 Repeat Example 7.16 for the following values
of the nondimensional ratios: k
21
0.5, L
21
2.0,
and v
r
1.5.
7.37 Repeat Example 7.15 when v
r
2.0 and
J
r
1.0.
7.38 An elastically supported machine tool with a
total mass of 4000 kg has a resonance frequency of
80 Hz. An 800 kg absorber system with a natural
frequency of 80 Hz is attached to the machine tool.
Determine the natural frequencies and mode shapes
of this system.
7.39 A six-cylinder, four-cycle engine driving a
generator is modeled
40
by using an eight degree-of-
freedom system shown in Figure E7.39. Free oscilla-
tions of this system are described by the following
system
where
3J 45f
$
6 3K
t
45f6 506
3K 4
EI
L
3
D
24 12 0 0
12 24 12 0
0 12 24 12
0012 12
T
FIGURE E7.34
y
1
y
2
y
3
m
2
m
1
LL L
m
3
7.35 The stiffness matrix for the system shown in Fig-
ure E7.14 is given by the following matrix
3J 4 H
210000000
021000000
002100000
000210000
000021000
000002100
000000980
000000049
X
kg
#
m
2
40
C. Genta, ibid.
