Balakumar Balachandran, Magrab E.B. Vibrations
Подождите немного. Документ загружается.


in which the jth equation has the form
(8.12)
In Eqs. (8.12), z
j
is the damping factor associated with the jth mode and v
j
is the
natural frequency associated with the jth mode. As discussed in Section 7.3.3,
since the damping matrix in Eq. (8.9) is diagonal, the system is said to have
modal damping.The coordinates h
j
,inwhichthe governingequations of motion
areuncoupled, arereferredto asthe principalcoordinatesormodalcoordinates.
The equation describing the oscillation in the jth mode has the form of the
governing equation of a single degree-of-freedom system, namely, Eq. (4.1).
Hence the solution for the response of the jth mode is given by Eq. (D.11a) if
0 z
j
1. Thus,
Response to initial conditions Response to forcing (8. 13)
where the constants A
j
and w
dj
are determined by the initial conditions,
(8.14a)
and the damped natural frequency v
dj
of the jth mode is given by
(8.14b)
From Eqs. (7.94), the modal damping factor z
j
is
(8.15)
where a and b are such that
In Section 8.2.2, we show how to obtain the initial modal displacements h
j
(0)
and initial modal velocities in terms of the system initial displacements
x
j
(0) and initial velocities .
Having determined the responses of the individual modes—that is,
h
j
(t)—we return to Eq. (8.2) and find that the system response can be con-
structed by making use of Eq. (7.31) as
(8.16)
Modal matrix Modal
Amplitudes
µ
x
1
1t 2
x
2
1t 2
o
x
N
1t 2
∂ 3£ 45h1t26 ≥
X
11
X
12
p
X
1N
X
21
X
22
p
X
2N
oo
∞
o
X
N1
X
N2
p
X
NN
¥µ
h
1
1t 2
h
2
1t 2
o
h
N
1t 2
∂
x
#
j
10 2
h
#
j
10 2
3C 4 a3M4 b3K4
z
j
1
2
a
a
v
j
bv
j
b
v
dj
v
j
21 z
2
j
w
dj
tan
1
v
dj
h
j
10 2
h
#
j
10 2 z
j
v
j
h
j
10 2
A
j
B
h
2
j
10 2 a
h
#
j
10 2 z
j
v
j
h
j
10 2
v
dj
b
2
h
j
1t 2 A
j
e
z
j
v
j
t
sin 1v
dj
t w
dj
2
1
v
dj
t
0
e
z
j
v
j
1tj2
sin 1v
dj
3t j42Q
j
1j 2dj
h
$
j
1t 2 2z
j
v
j
h
#
j
1t 2 v
2
j
h
j
1t 2 Q
j
1t 2
j 1, 2, . . . , N
440 CHAPTER 8 Multiple Degree-of-Freedom Systems
⎫
⎬
⎭
⎫
⎪
⎪
⎬
⎪
⎪
⎭
⎫
⎪
⎪
⎬
⎪
⎪
⎭
⎫
⎪
⎪
⎪
⎪
⎬
⎪
⎪
⎪
⎪
⎭

where
Component of response Component of response Component of response
in the first mode in the second mode in the Nth mode
i 1,2,... ,N (8.17)
Equation (8.16) is rewritten in the compact form
(8.18)
Oscillation in the
jth mode
We see from Eq. (8.18) that the displacement of each mass x
i
(t) is composed
of response components in the different modes of the vibratory system. Thus,
the response of a multi-degree-of-freedom system is a weighted combination
of the individual modes of the system. The modal amplitude provides the
weighting for each mode.
Response of Damped System
On substituting Eq. (8.13) into Eq. (8.18), we see that the response of the lin-
ear multi-degree-of-freedom system given by Eq. (8.1) takes the form
(8.19)
where the elements of {x(t)} are
Response of Undamped System
When the system is undamped, we set z
j
0 in Eq. (8.19), note that v
dj
v
j
from Eq. (8.14b), and obtain
(8.20)5x1t 26
a
N
j1
5X6
j
cA
j
sin1v
j
t w
j
2
1
v
j
t
0
sin1v
j
3t j42Q
j
1j 2dj d
1
v
dj
t
0
e
z
j
v
j
1tj2
sin1v
dj
3t j42Q
j
1j 2dj d
x
i
1t 2
a
N
j1
X
ij
cA
j
e
z
j
v
j
t
sin1v
dj
t w
dj
2
1
v
dj
t
0
e
z
j
v
j
1tj2
sin 1v
dj
3t j42Q
j
1j 2dj d
5x1t26
a
N
j1
5X6
j
cA
j
e
z
j
v
j
t
sin 1v
dj
t w
dj
2
5x1t26
a
N
j1
5X6
j
h
j
1t 2
X
i1
h
1
1t 2
X
i2
h
2
1t 2
###
X
iN
h
N
1t 2
x
i
1t 2
a
N
j1
X
ij
h
j
1t 2
8.2 Normal-Mode Approach 441
⎫
⎬
⎭
⎫
⎬
⎭
⎫
⎬
⎭
⎫
⎬
⎭

where from Eqs. (8.14a), we find that
(8.21)
8.2.2 Response to Initial Conditions
When the forcing is zero—that is, {F} {0} in Eq. (8.1)—then the modal
forced vector {Q} {0} in Eq. (8.7), and the response of the system follows
from Eq. (8.19) as
(8.22)
Free oscillation component in the jth mode
where A
j
and w
dj
are determined from Eqs. (8.14a) in terms of the initial dis-
placement and the initial velocity. For 0 z
j
1, Eq. (8.22) consists of a sum
of damped sinusoids associated with the individual modes. The damped nat-
ural frequency v
dj
of the jth mode is given by Eq. (8.14b).
For the determination of w
dj
in Eqs. (8.14a), the proper quadrant as de-
termined by the sign of the numerator and the denominator must be used. For
example, when we see that the quadrant is determined by the sign
of h
j
(0); when h
j
(0) 0, w
dj
is in the first quadrant and when h
j
(0) 0, w
dj
is in the third quadrant.
The initial conditions and and h
j
(0) can now be determined from
Eq. (8.2) in the following manner. We note from Eq. (8.18) that
(8.23)
If we pre-multiply Eqs. (8.23) by that is,
(8.24)
and make use of the orthogonality of the modes given by Eq. (7.62) and the
modal mass given by Eqs. (7.67), we obtain
(8.25)
If the modes are normalized with respect to the mass matrix, then .M
ˆ
jj
1
h
#
j
10 2 5X6
T
j
3M 45x
#
10 26/M
ˆ
jj
h
j
10 2 5X6
T
j
3M 45x1026/M
ˆ
jj
5X6
T
i
3M 45x
#
10 26
a
N
j1
5X6
T
i
3M 45X6
j
h
#
j
10 2
5X6
T
i
3M 45x1026
a
N
j1
5X6
T
i
3M 45X6
j
h
j
10 2
5X6
T
i
3M 4;
5x
#
10 26
a
N
j1
5X6
j
h
#
j
10 2
5x1026
a
N
j1
5X6
j
h
j
10 2
h
#
j
10 2
h
#
j
10 2 0,
5x1t26
a
N
j1
5X6
j
A
j
e
z
j
v
j
t
sin 1v
dj
t w
dj
2
w
j
tan
1
v
j
h
j
10 2
h
#
j
10 2
A
j
B
h
2
j
10 2 a
h
#
j
10 2
v
j
b
2
442 CHAPTER 8 Multiple Degree-of-Freedom Systems
⎫
⎪
⎪
⎪
⎬
⎪
⎪
⎪
⎭

Free Oscillations for a Special Case
Now we consider the special case where the initial velocity ,
and the system is provided an initial displacement in its nth mode shape;
that is,
(8.26)
From Eqs. (7.62) and (7.67), we find that
(8.27)
where the Kronecker delta function d
nj
0, n j and d
nj
1, n j. Then,
from Eqs. (8.25), we find that the initial modal displacement and initial modal
velocity are given by, respectively,
(8.28)
Therefore, the only mode for which the associated initial condition is not
equal to zero is the one corresponding to the nth mode shape, and it follows
that the only mode that has a non-zero response is h
n
(t). Then, from Eq. (8.18)
{x(t)} {X}
n
h
n
(t) (8.29)
where h
n
is found from Eq. (8.13) as
h
n
(t) A
n
e
z
n
v
n
t
sin(v
dn
t w
dn
) (8.30)
and from Eqs. (8.14a), (8.14b), and (8.28) we obtain
(8.31)
In other words, the system only oscillates in its nth mode shape; none of the
other modes is excited.
EXAMPLE 8.1
Undamped free oscillations of a two degree-of-freedom system
We return to the system shown in Figure 7.1 and consider the case when the
forcing and the damping are absent. We shall find the response of the system
when the initial conditions are as follows
(a)5x10 26 e
x
10
x
20
f
and
5x
#
10 26 e
x
#
10
x
#
20
f
w
dn
tan
1
v
dn
h
n
10 2
z
n
v
n
h
n
10 2
tan
1
21 z
2
n
z
n
A
n
B
h
2
n
10 2 a
z
n
v
n
h
n
10 2
v
dn
b
2
h
n
10 2
21 z
2
n
a
o
21 z
2
n
h
#
j
10 2 0
h
j
10 2 a
o
d
nj
1
M
ˆ
jj
5X6
T
j
3M 45X6
n
d
nj
5x1026 a
o
5X6
n
5x
#
10 26 506
8.2 Normal-Mode Approach 443

The response in this case is determined by making use of the general solution
given by Eqs. (8.20) and (8.21) for the undamped system; that is,
(b)
where
(c)
The initial conditions from the modes h
j
(0) and are determined from
Eqs. (8.25) as
(d)
Thus, from Eq. (b) the undamped oscillations of the system are described as
the weighted sum of the free oscillations of the first and second modes of the
system.
EXAMPLE 8.2
Damped and undamped free oscillations of a two
degree-of-freedom system
We now continue with Examples 7.14 and 7.20 and assume that damping is
present in the form of Eq. (7.104) with z 0.05. The damped and undamped
free responses of the system are determined for the initial conditions
(a)
The response of the system has the form of Eq. (8.20) for the undamped
case and Eq. (8.19) for the damped case. Based on the information in Exam-
ple 7.12 and from Eqs. (a) and (d) of Example 8.1, we find that the initial
modal velocities and the initial modal displacements h
j
(t) are
(b) 0.056
h
2
10 2 5X6
T
2
3M 45x1026/M
ˆ
22
1
10.311
a
52.518 16
c
1.2 0
0 2.7
de
0.1
0.1
fb
0.045
h
1
10 2 5X6
T
1
3M 45x1026/M
ˆ
11
1
3.658
a
50.893 16
c
1.2 0
0 2.7
de
0.1
0.1
fb
h
#
j
10 2 0
e
x
10
x
20
f e
0.1
0.1
f m
and
e
x
#
10
x
#
20
f e
0
0
f m/s
h
#
j
10 2
1
M
ˆ
jj
5X6
T
j
3M 4e
x
#
10
x
#
20
f
h
j
10 2
1
M
ˆ
jj
5X6
T
j
3M 4e
x
10
x
20
f
h
#
10 2
w
dj
tan
1
v
j
h
j
10 2
h
#
j
10 2
A
j
B
h
2
j
10 2
h
#
2
j
10 2
v
2
j
5x1t26
a
2
j1
5X6
j
A
j
sin 1v
j
t w
dj
2
444 CHAPTER 8 Multiple Degree-of-Freedom Systems

where from Eq. (b) of Example 7.14 we have determined that
Response for Damped Case
For z 0.05 and from Eq. (d) of Example 7.4, we obtain
(c)
From Eqs. (8.14), we compute the damped natural frequencies v
dj
and the
phases w
dj
as
(d)
and the amplitudes A
j
as
(e)
Then, from Eq. (8.13), in the absence of forcing (i.e., Q
j
0), we ob-
tain the modal responses and compute them based on Eqs. (c), (d), and (e),
as follows.
(f)h
2
1t 2 A
2
e
zv
2
t
sin1v
d2
t w
d2
2 0.056e
0.281t
sin15.616t 1.621 2
h
1
1t 2 A
1
e
zv
1
t
sin1v
d1
t w
d1
2 0.045e
0.126t
sin12.516t 1.621 2
0.056
A
2
B
h
2
2
10 2 a
zv
2
h
2
10 2
v
d2
b
2
B
10.056 2
2
a
0.056 0.281
5.616
b
2
0.045
A
1
B
h
2
1
10 2 a
zv
1
h
1
10 2
v
d1
b
2
B
10.045 2
2
a
0.045 0.126
2.516
b
2
tan
1
21 0.05
2
0.05
1.621
rad
w
d2
tan
1
v
d2
h
2
10 2
zv
2
h
2
10 2
tan
1
h
2
10 221 z
2
zh
2
10 2
tan
1
21 0.05
2
0.05
1.621
rad
w
d1
tan
1
v
d1
h
1
10 2
zv
1
h
1
10 2
tan
1
h
1
10 221 z
2
zh
1
10 2
v
d2
v
2
21 z
2
5.62321 0.05
2
5.616
rad/s
v
d1
v
1
21 z
2
2.51921 0.05
2
2.516
rad/s
zv
2
0.05 5.623 0.281
zv
1
0.05 2.519 0.126
3£ 4 c
0.893 2.518
11
d
8.2 Normal-Mode Approach 445
The free response of the damped system is determined from Eq. (8.22) and
Eqs. (f). Thus,
(g)
and
(h)
Response for Undamped Case
The results for the undamped case are computed as follows. From Eqs. (b)
and (e), with z 0, we have
(i)
and from Eqs. (d), we obtain
(j)
Then, from Eq. (8.22) with z
j
0 and Eqs. (i) and ( j), we obtain
(k)
and
(l)
In the damped case, the response given by Eqs. (g) and (h) consists of expo-
nentially decaying sinusoidal oscillations in each mode. In the undamped
case, the response given by Eqs. (k) and (l) consists of harmonic oscillations
in each mode.
0.045 cos12.516t2 0.056 cos15.623t 2
m
0.045 1 cos12.516t 2 0.056 1 cos15.623t 2
x
2
1t 2 A
1
X
21
sin1v
1
t p/22 A
2
X
22
sin1v
2
t p/22
0.040 cos12.516t2 0.140 cos15.623t 2
m
0.045 0.893 cos12.516t 2 0.056 2.518 cos15.623t2
x
1
1t 2 A
1
X
11
sin1v
1
t p/22 A
2
X
12
sin1v
2
t p/22
w
d2
p/2
w
d1
p/2
v
d2
v
2
5.623
v
d1
v
1
2.519
A
2
0.056
A
1
0.045
0.056e
0.281t
sin15.616t 1.621 2
m
0.045e
0.126t
sin12.516t 1.621 2
0.056 1 e
0.281t
sin15.616t 1.621 2
0.045 1 e
0.126t
sin12.516t 1.621 2
A
1
X
21
e
zv
1
t
sin1v
d1
t w
d1
2 A
2
X
22
e
zv
2
t
sin1v
d2
t w
d2
2
x
2
1t 2 h
1
1t 2X
21
h
2
1t 2X
22
0.140e
0.281t
sin15.616t 1.621 2
m
0.040e
0.126t
sin12.516t 1.621 2
0.056 2.518 e
0.281t
sin15.616t 1.621 2
0.045 0.893 e
0.126t
sin12.516t 1.621 2
A
1
X
11
e
zv
1
t
sin1v
d1
t w
d1
2 A
2
X
12
e
zv
2
t
sin1v
d2
t w
d2
2
x
1
1t 2 h
1
1t 2X
11
h
2
1t 2X
12
446 CHAPTER 8 Multiple Degree-of-Freedom Systems
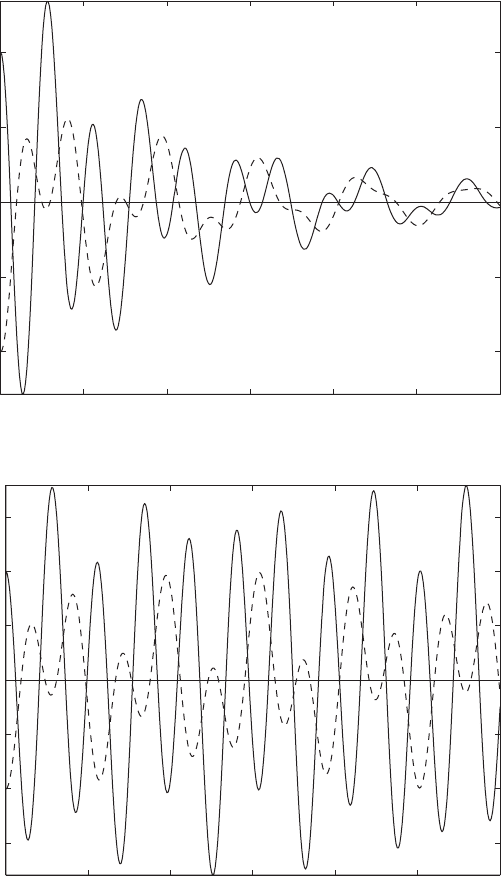
The time histories given by Eqs. (g) and (h) for the damped case are plot-
ted in Figure 8.1, and the time histories given by Eqs. (k) and (l) for the un-
damped case are plotted in Figure 8.2. Comparing Figures 8.1 and 8.2, we see
that in the damped case, the displacements x
1
(t) and x
2
(t) approach zero as
; that is, the system eventually settles down to the equilibrium position.
This is not true in the undamped case.
t 씮 q
8.2 Normal-Mode Approach 447
0 2 4 6 8 10 12
0.1
0.05
0
0.05
0.1
t
x
1
(t),x
2
(t)
0 2 4 6 8 10 12
0.15
0.1
0.05
0
0.05
0.1
0.15
t
x
1
(t),x
2
(t)
FIGURE 8.1
Displacements of a two degree-of-
freedom system with z 0.05
when both masses are subjected to
equal, but opposite, initial displace-
ments. [Solid line x
1
(t); dashed line
x
2
(t).]
FIGURE 8.2
Displacements of a two degree-of-
freedom system with z 0 when
both masses are subjected to equal,
but opposite, initial displacements.
[Solid line x
1
(t); dashed line x
2
(t).]
8.2.3 Response to Harmonic Forcing and the
Frequency-Response Function
In this section, we determine the response of the physical systems described
by Eq. (8.1) to harmonic forcing. First, we consider the response of undamped
systems and illustrate how the frequency-response function can be con-
structed from this response. The notion of resonance in a multiple degree-of-
freedom system is also discussed. A direct approach that can be used to ob-
tain the forced response of a multiple degree-of-freedom system is presented
and it is followed by a presentation of the normal-mode approach. Propor-
tionally damped systems are treated at the end of the section.
Undamped Systems: Direct Approach
For illustration, we consider the two degree-of-freedom system shown in Fig-
ure 7.1 without damping; that is, c
1
c
2
c
3
0 in Eq. (7.1b), and let the
forcing be of the form
(8.32)
where F
j
are constants. Then, the governing equations of motion given by
Eq. (7.1b) reduce to
(8.33)
To determine a response of the two degree-of-freedom system to this forcing,
a solution of the form
(8.34)
is assumed where X
1
and X
2
are to be determined. Equation (8.34) means that
the masses m
1
and m
2
in Figure 7.1 are assumed to respond at the same
frequency as the excitation frequency v. Furthermore, this solution form is
consistent with the discussion presented in Section 5.2 where harmonically
forced single degree-of-freedom systems were considered. On substituting
Eq. (8.34) into Eq. (8.33) and canceling the common factor cos vt on both
sides of the equation, we arrive at
(8.35)
After using the nondimensional quantities given by Eqs. (7.41), Eq. (8.35) is
recast into the form
(8.36) v
2
r
X
1
3v
2
r
11 k
32
2
2
4X
2
v
2
r
F
2
/k
2
31 v
2
r
m
r
2
4X
1
m
r
v
2
r
X
2
F
1
/k
1
c
k
1
k
2
v
2
m
1
k
2
k
2
k
2
k
3
v
2
m
2
de
X
1
X
2
f e
F
1
F
2
f
e
x
1
1t 2
x
2
1t 2
f e
X
1
X
2
fcos vt
c
m
1
0
0 m
2
de
x
$
1
x
$
2
f c
k
1
k
2
k
2
k
2
k
2
k
3
de
x
1
x
2
f e
F
1
F
2
fcos vt
f
2
1t 2 F
2
cos vt
f
1
1t 2 F
1
cos vt
448 CHAPTER 8 Multiple Degree-of-Freedom Systems

8.2 Normal-Mode Approach 449
Solving for X
j
from Eqs. (8.36), we obtain
(8.37)
where the term in the denominator has the form
(8.38)
and a
1
and a
2
are given by Eqs. (7.46). When D
o
0, we have the character-
istic equation given by Eq. (7.45).
From Eqs. (8.37), it is evident that whenever the excitation frequency v
is equal to a natural frequency of the system, that is, when v v
1
or v v
2
,
the displacement responses X
j
become infinite; hence, each of these frequency
relationships between the excitation frequency and a system natural fre-
quency is called a resonance relation and at these excitation frequencies, the
system is said to be in resonance. In Chapter 5, it was seen that for a linear
single degree-of-freedom system there is one excitation frequency at which
we have a resonance. Since a linear two degree-of-freedom system has two
natural frequencies, there are two excitation frequencies at which we can have
a resonance. By extension, since a linear system with N degrees of freedom
has N natural frequencies, there are N excitation frequencies at which we can
have a resonance. It is also noted from the stability discussion of Section 7.5
that an undamped multiple degree-of-freedom system is unbounded when ex-
cited at one of its resonances.
In a manner similar to that for a single degree-of-freedom system, we
construct the system frequency-response functions. To this end, we set F
2
0
in Eqs. (8.37) and obtain
(8.39)
Similarly, setting F
1
0 in Eqs. (8.37), we find that
(8.40)
In Eqs. (8.39) and (8.40), the frequency-response functions H
ij
() are
nondimensional, the subscript i is associated with the response of inertial el-
ement m
i
and the subscript j is associated with the force input to the inertial
element m
j
. Transfer functions and associated frequency-response functions
are obtained for more general cases in Section 8.5.
X
2
F
2
/k
2
H
22
1 2
v
2
r
11 v
2
r
m
r
2
2
D
o
X
1
F
2
/k
2
H
12
1 2
m
r
v
4
r
D
o
X
2
F
1
/k
1
H
21
1 2
v
2
r
D
o
X
1
F
1
/k
1
H
11
1 2
v
2
r
11 k
32
2
2
D
o
D
o
4
a
1
2
a
2
X
2
v
2
r
D
o
31F
1
/k
1
2 1F
2
/k
2
231 v
2
r
m
r
2
44
X
1
1
D
o
31F
1
/k
1
23v
2
r
11 k
32
2
2
4 1F
2
/k
2
2m
r
v
4
r
4
