Balakumar Balachandran, Magrab E.B. Vibrations

Подождите немного. Документ загружается.

By using Eqs. (f) in Eqs. (8.66), which give the displacements of the individ-

ual inertial elements in the Laplace transform domain, we arrive at

(g)

Upon taking the inverse Laplace transform of Eqs. (g) numerically,

we ob-

tain the results shown in Figure 8.1.

In the absence of damping, c

 c

 0, and Eqs. (f ) and (g) be-

come, respectively,

(h)

and

(i)

Again taking the inverse Laplace transform of Eqs. (i) numerically, we obtain

the results shown in Figure 8.2.

We now consider the two degree-of-freedom system with the same mass

and stiffness matrices as before, but with a different damping matrix. In par-

ticular, we use the damping values of the arbitrary damping case of Example

8.9; that is, the values of the values of c

and c

remain the same as in Eqs. (d)

while c

 0.49 N s/m. In this case, we ﬁnd that c

 1.33 and z

 0.0334.

Making the appropriate substitutions and taking the inverse Laplace trans-

form numerically produces the same results as those shown in Figure 8.7b.

We note that the Laplace transform method does not require any restrictions

to be placed on the form of the viscous damping matrix.

8.4.3 Force Transmitted to a Boundary

Once the responses to certain forcing conditions and/or certain initial condi-

tions are determined, one may also determine the force transmitted to a ﬁxed

boundary such as the left end in Figure 8.8. In this case, from a free-body di-

agram of mass m

, the force transmitted is

1s 2

10.1s

 0.2112s

 4.556s

 2.889

1s 2

10.1s

 0.04442s

 4.556s

 2.889

1s 20.1s

1s 2 0.1s

1s 2 s

 4.556s

 2.889

E1s2 s

 1.556

C1s2 0.889

B1s2 2

A1s2 s

 3

1s 2

0.1s

 0.0282s

 0.213s  0.0229

 0.282s

 4.573s

 0.4792s  2.889

1s 2

0.1s

 0.0282s

 0.0427s  0.0076

 0.282s

 4.573s

 0.4792s  2.889

480 CHAPTER 8 Multiple Degree-of-Freedom Systems

The function ilaplace from MATLAB’s Symbolic Toolbox was used.

(8.89a)

which, in terms of the nondimensional time t takes the form

(8.89b)

Taking the Laplace transforms of both sides of Eq. (8.89b), we obtain

(8.90)

where X

(s) is given by Eqs. (8.66). Once F

base

(s) is determined, the corre-

sponding time information is determined from

(8.91)

The transmitted force given by Eqs. (8.89) is used in Section 8.7, where

we address the notion of transmissibility ratio.

8.5 TRANSFER FUNCTIONS AND FREQUENCY-RESPONSE FUNCTIONS

In Sections 5.3 and 6.2, we considered transfer functions associated with

single degree-of-freedom systems and explained the relationship between a

frequency-response function and a transfer function. In Section 8.2.3, we il-

lustrated how frequency-response functions associated with a two degree-

of-freedom system were constructed from the response to a harmonic excita-

tion. Here, we discuss further frequency-response functions for two degree-of-

freedom systems. The nature of the relationship between a frequency-response

function and a transfer function is also addressed. The fundamental nature of

this relationship remains the same as that discussed for a single degree-of-

freedom system. However, in the case of a multi-degree-of-freedom system,

due to the presence of more than one inertial element, one deals with more than

one transfer function and more than one frequency-response function.

As in the case of vibratory systems described by linear single degree-of-

freedom systems, the responses of vibratory systems described by linear

multi-degree-of-freedom systems can be determined if the transfer functions

for the systems are known. For this reason, the material presented here pro-

vides a basis for the discussions

on mechanical ﬁlters later in this section,

vibration absorbers in Section 8.6, transmissibility ratio in Section 8.7, and

the moving base model in Section 8.8.

We now obtain expressions for the transfer functions associated with the

inertial elements m

and m

shown in Figure 8.8. We ﬁrst set the initial

base

1t 2 L

1

base

1s 24

base

1s 2 k

312z

s  12X

1s 2 2z

10 24

base

1t 2 k

c2z

 x

base

1t 2 c

 k

8.5 Transfer Functions and Frequency-Response Functions 481

If one goes back to Section 8.4 after completing this section, it will be seen that the notion of a

transfer function was used in determining the numerical results for responses in the presence of

different initial conditions and different forcing conditions.

conditions to zero, assume that k

 c

 0 for convenience, and use Eqs.

(8.65), (8.66), (8.74), and (8.82) to arrive at

(8.92)

Equations (8.92) will be used to determine four transfer functions, one

pair associated with the forcing applied to one inertial element (say, m

Figure 8.8) and the other pair associated with the forcing applied to the other

inertial element. As discussed in Section 6.2 for a single degree-of-freedom

system, an impulse force can be used to determine a transfer function. We de-

termine the transfer functions G

(s) where the subscript i refers to the re-

sponse (or output) location and the subscript j refers to the force (or input) lo-

cation. Therefore, to determine the ﬁrst pair of transfer functions, an impulse

forcing is applied to mass m

; that is,

(8.93)

Then, we have

(8.94)

where

(8.95)

Making use of Eqs. (8.92), (8.94), and (8.95), we ﬁnd that

(8.96)

Similarly, we determine the other pair of transfer functions by applying

an impulse forcing to mass m

; that is,

(8.97)

Then, we have

1t 2 F

d1t 2

1t 2 0

1s 2

C1s 2

1s 2

1s 2

1s 2

1s 2 F

1s 2

1s 2

m/N

1s 2

1s 2

m/N

1t 2 0

1t 2 F

d1t 2

1s 2

1s 2

1s 2C1s2 F

1s 2A1s2/m

1s 2

1s 2

1s 2E

1s 2 F

1s 2B1s2/m

482 CHAPTER 8 Multiple Degree-of-Freedom Systems

It should be clear from the form of Eqs. (8.94) that excitations other than impulse excitations

can also be used to determine the transfer functions G

(s).

(8.98)

where

(8.99)

Making use of Eqs. (8.92), (8.98), and (8.99), we ﬁnd that

(8.100)

From the form of Eqs. (8.96) and (8.100), it is evident that the polynomial

(s) appears in the denominator of each transfer function; this is the same

polynomial that is associated with the characteristic equation of this two

degree-of-freedom system.

Note that Eqs. (8.62) are written in terms of the nondimensional time t

instead of t before the Laplace transforms were executed. Therefore, the

frequency-response functions are given by G

( jv/v

) or G

( j), where

v/v

is the nondimensional frequency ratio. (See Laplace transform

pair 1 in Table A of Appendix A.) Hence, the frequency-response functions

are determined from Eqs. (8.96) and (8.100) to be

(8.101)

where the terms in the numerators and the denominators are given by

(8.102)

 2z

4v

 31  m

 v

 4z

4

 j32z

1j2

 j32z

 2z

4

1j2

 2z

jv

C1j2 2z

jv

B1j 2 2z

jm

A1j 2

 21z

 z

2j1  m

1j2

A1j2

1j2

1j2

B1j2

1j2

 k

1j2

1j2

C1j2

1j2

1j2

1j2

1s 2

A1s 2

1s 2

1s 2

B1s 2

1s 2

1s 2 F

1s 2

1s 2

m/N

1s 2

1s 2

m/N

8.5 Transfer Functions and Frequency-Response Functions 483

When the damping is absent, D

( j) given by the last of Eqs. (8.102) reduces

to the characteristic equation, Eq. (7.45), when the spring k

is absent.

The magnitudes of the frequency-response functions are given by

(8.103)

and the associated phase responses are given by

(8.104)

Notice that H

is a nondimensional quantity.

As discussed in Section 5.3 for a single degree-of-freedom system and in

Section 8.2.3 for a two degree-of-freedom system, frequency-response func-

tions can also be constructed from responses to harmonic excitations. This

can be used to interpret Eqs. (8.103) and (8.104) in the following manner. Let

us suppose that a harmonic excitation of the following form acts on the sys-

tem shown in Figure 8.8:

(8.105)

Then, H

() and H

() represent the amplitude-response functions of the in-

ertia elements m

and m

, respectively. These amplitude-response functions are

functions of the excitation frequency v or, in the nondimensional form, the fre-

quency ratio . The associated phase-response functions of the inertia ele-

ments m

and m

are given by w

() and w

(), respectively. Similarly, the

amplitude-response functions H

() and H

() provide the amplitudes of the

responses of the inertia elements m

and m

, respectively, when a harmonic ex-

citation of the following form is imposed on the system shown in Figure 8.8.

(8.106)

The associated phase-response functions of the inertia elements m

and m

are

given by w

() and w

(), respectively.

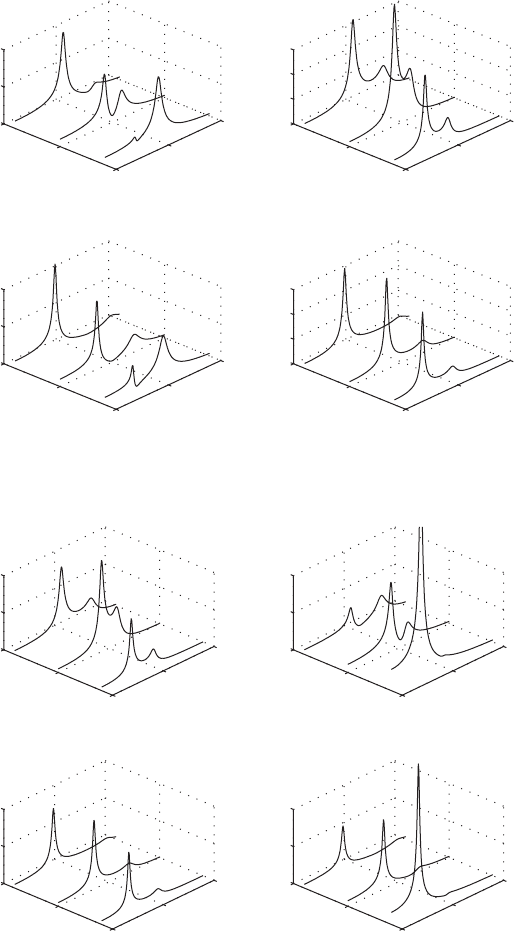
In Figure 8.12, for the case where k

 c

 0, the nondimensional

amplitude-response functions H

() are plotted as a function of the excitation

frequency ratio  and the system frequency ratio v

. These plots are graphs

of the functions given by Eqs. (8.103). Since the system is damped, the am-

plitude responses of the inertia elements m

and m

have ﬁnite values for all

values of the excitation frequency. For “small” values of v

, it is seen that the

response of one of the inertia elements is pronounced at and close to the lower

resonance, while the response of the other inertia element is pronounced at

and close to the higher resonance. As the excitation-frequency ratio  is in-

creased past the higher resonance value, the responses of both inertia ele-

ments are relatively uniform, as was the case for responses of damped single

degree-of-freedom systems forced by harmonic excitations.

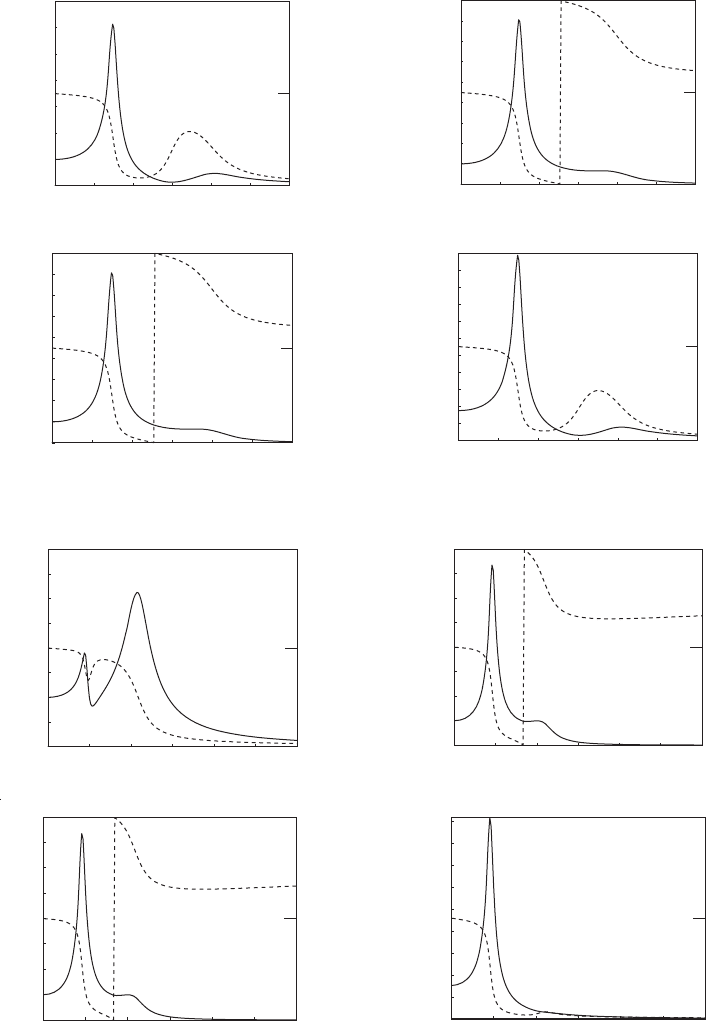
In Figure 8.13, the amplitude responses are shown along with the

associated phase responses. These responses have been generated by using

1t 2 F

cos 1vt 2

1t 2 F

cos 1t 2

1t 2 0

1t 2 F

cos 1vt 2

1t 2 F

cos 1t 2

1 2 tan

1

Im3G

1j24

Re3G

1j24

1 2 k

1j20

i, l  1, 2

484 CHAPTER 8 Multiple Degree-of-Freedom Systems

0.5

1.5

Ω

 0.1 m

 0.1

 0.5 m

 0.5



(Ω)H

(Ω)

(Ω)H

(Ω)

0.5

1.5

Ω

0.5

1.5

Ω

0.5

(a)

1.5

Ω

0.5

1.5

Ω

0.5

1.5

100

Ω

0.5

1.5

Ω

0.5

(b)

1.5

Ω

 0.1

 0.5 m

 0.5

 0.1



(Ω)H

(Ω)

(Ω)H

(Ω)

FIGURE 8.12

Magnitudes of frequency-response functions for the two masses shown in Figure 8.8 when

 c

 0, z

 z

 0.05, and m

 0.1 or 0.5: (a) H

(), n  1, 2 and (b) H

(),

n  1, 2. The frequency-response functions are shown for v

 0.6, 1.0, and 1.4.

0 0.5 1 1.5 2 2.5 3



180

Phase(°) Phase(°)

Phase(°)

Phase(°) Phase(°)

Phase(°)

Ω

(a)

0.5

1.5

2.5

3.5

(b)



180



180



180



180



180



180

0 0.5 1 1.5 2 2.5 3

Ω

0 0.5 1 1.5 2 2.5 3

Ω

0 0.5 1 1.5 2 2.5 3

Ω

0 0.5 1 1.5 2 2.5 3

Ω

0 0.5 1 1.5 2 2.5 3

Ω

00.511.522.5 3

Ω

0 0.5 1 1.5 2 2.5 3

Ω

(Ω

)

(Ω

)

(Ω

)

(Ω

)

(Ω

)

(Ω

)

(Ω

)



180

(Ω)

FIGURE 8.13

Frequency-response functions for the two masses shown in Figure 8.8 as a function of v/v

when k

 c

 0, z

 z

 0.1,

and m

 0.6: (a) v

 1.5 and (b) v

 0.5. [The solid lines represent amplitude responses and the dashed lines represent phase

responses.]

Eqs. (8.103) and (8.104). Phase shift characteristics as seen in Chapter 5 for

a harmonically forced single degree-of-freedom system at resonance can be

seen at the two resonance frequency locations for the two degree-of-freedom

system. The phase at each resonance is either 90° or 90°.

System Identiﬁcation

For constructing Figures 8.12 and 8.13, the system parameters were assumed

and substituted into Eqs. (8.103) and (8.104). In practice, one often measures

frequency-response functions and then determines the system parameters, as

discussed in Section 5.3 for single degree-of-freedom systems. This approach

to the problem is the inverse of the approach that we have taken so far; that is,

going from measurements to the determination of system parameters rather

than going from system parameters to response predictions. Thus, if a linear

vibratory model is assumed to represent the physical system, then one ﬁts the

measurement data with functions such as those given by Eqs. (8.103) and

(8.104) to obtain an estimate for the system parameters. This topic falls under

the purview of modal analysis

and system identiﬁcation.

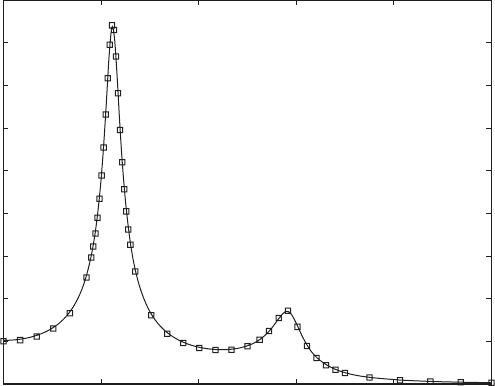
To illustrate the determination of the parameters of a two degree-of-

freedom system from measured data, consider the experimental data shown by

the squares in Figure 8.14. They were obtained by applying a harmonically

varying force of measured magnitude F(v) at the frequency v to mass m

and

measuring the displacement response of mass m

at this frequency. The ratio of

these two measured quantities at each value of v is represented by the squares

8.5 Transfer Functions and Frequency-Response Functions 487

0 200 400 600 800 1000

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

v (rad/s)

(

) × 10

FIGURE 8.14

Experimentally obtained data values and the result after ﬁtting a model to them.

D. Ewins, Modal Testing: Theory and Practice, John Wiley & Sons, NY (1984).

in Figure 8.14. In order to determine the system’s properties, we use the model

represented by H

(v) and ﬁt the data to this model. From Eqs. (8.103), the

quantity H

(v)is

From this equation and Eqs. (8.102), we see that there are six parameters to

be determined from the curve-ﬁtting procedure, namely k

, v

, z

, m

, and

. The known values are H

(v) and v. By using the results of standard curve

ﬁtting procedures

we ﬁnd that k

 9797.3 N/m, v

 250.5 rad/s,

 0.082, z

 0.041, m

 0.204, and v

 2.095. We now use the rela-

tions given by Eqs. (7.41) and (8.61) to determine the remaining parameters.

Thus, from k

and v

we obtain m

 0.156 kg; from m

and m

we obtain

 0.032 kg; from v

and v

we obtain v

 524.8 rad/s; from m

and v

we obtain k

 8765.3 N/m; from z

, v

, and m

we obtain c

 6.45 N s/m;

and from z

, v

, and m

we obtain c

 1.37 N s/m.

EXAMPLE 8.11

Frequency-response functions for system with bounce

and pitch motions

In this example, we revisit the physical system shown in Figure 7.5 when a

force f(t) and a moment m(t) are imposed at the location G. Although the as-

sumed forcing and moment inputs are not realistic, they have been considered

to illustrate how frequency-response functions can be constructed. To deter-

mine these frequency-response functions, we ﬁrst obtain the governing equa-

tions of the system for “small” oscillations. We then take the Laplace trans-

forms of these equations to obtain the associated transfer functions. The

frequency-response functions are determined from these transfer functions.

We also illustrate how a sensor measurement can be represented in terms of

the system frequency-response functions.

The governing equations for the unforced case have been obtained in

Eq. (k) of Example 7.3. We modify Eq. (k) to include the force f(t) and the

moment m(t) to obtain the following governing equations:

(a)

If we denote the Laplace transforms of, , , f(t), and m(t)by , ,

F(s), and M(s), respectively, then upon taking the Laplace transform of Eq. (a)

and assuming that the initial conditions are zero, we arrive at

1s 2Y

1s 2u

1t 2y

1t 2

 c

 k

1k

 k

1k

 k

2 1k

 k

f e

f 1t 2

m1t 2

m 0

0 J

f c

 c

1c

 c

1c

 c

21c

 c

1v/v

2 `

C1jv/v

1jv/v

488 CHAPTER 8 Multiple Degree-of-Freedom Systems

The function lsqnonlin from MATLAB’s Optimization Toolbox was used. For this model,

the procedure is very sensitive to the initial guesses and must be employed interactively in order

to obtain a satisfactory residual.

(b)

From Eq. (b), we ﬁnd that

(c)

where the transfer functions G

(s) are given by the following expressions:

(d)

and the polynomial D(s) is given by

(e)

The frequency-response functions G

( jv) are determined by setting s  jv

in Eqs. (d) and (e).

Let us suppose that an acceleration sensor is located at a distance L

sensor

to the right of the point G in Figure 7.5. Then the acceleration measured by

the sensor is

(f)

We shall determine how the frequency information in the sensor measurement

is related to the frequency information in the forcing by making use of the fre-

quency-response functions given by Eqs. (d). Upon taking the Laplace trans-

form of Eq. (f) and assuming zero initial conditions, we arrive at

(g)

For illustrative purposes, we assume that the excitation moment m(t)  0;

hence, M(s)  0. Making use of Eq. (c) to express the responses and

in terms of the applied forcing, we arrive at

(h)

where the transfer functions G

(s) in Eq. (h) are given by Eqs. (d). Upon sub-

stituting Eqs. (h) into Eq. (g), we arrive at

(i)A

1s 2 s

1s 2 L

sensor

1s 24F1s2

1s 2 G

1s 2F1s2

1s 2 G

1s 2F1s2

1s 2Y

1s 2

1s 2 s

1s 2 L

sensor

1s 22

1t 2 y

1t 2

 L

sensor

1t 2

31c

 c

2s  1k

 k

D1s 2 3J

 1c

 c

2s  1k

 k

243ms

 1c

 c

2s  k

 k

1s 2

 1c

 c

2s  k

 k

D1s 2

1s 2 G

1s 2

 c

2s  1k

 k

D1s 2

1s 2

 1c

 c

2s  1K

 K

D1s 2

1s 2

f c

1s 2 G

1s 2

1s 2 G

1s 2

F1s 2

M1s 2

 e

1s 2

f e

F1s 2

m1s 2

 1c

 c

2s  k

 k

1c

 c

2s  1k

 k

1c

 c

2s  1k

 k

2 J

 1c

 c

2s  1k

 k

8.5 Transfer Functions and Frequency-Response Functions 489