Balakumar Balachandran, Magrab E.B. Vibrations
Подождите немного. Документ загружается.

resonance frequencies. Based on Eq. (8.110a), it is clear that when z
2
0, the
response of the primary system is zero. However, when z
2
0 and/or if the
nondimensional excitation frequency is different from 1, the response
of the primary system may not have a “small” magnitude. Therefore, we
would like to choose the absorber system parameters so that the response of
the primary system is as small as possible over a wide frequency range that
includes 1.
For the general case, when the damping factor z
1
of the primary system
is not zero, the choice of the secondary system parameters cannot be put in
explicit form such as Eq. (8.111) and one has to resort to numerical means.
However, when z
1
0, one can obtain
20
optimal values for the secondary sys-
tem natural frequency and the secondary system damping ratio to tailor the
amplitude response H
11
() of the primary system. The optimal values for the
absorber system parameters are obtained when the values of the peaks shown
in Figure 8.21 are equal; that is, when
(8.117)
Upon carrying out the derivation, the following optimal values are obtained:
21
(8.118)v
r,opt
1
1 m
r
and
z
2,opt
B
3m
r
811 m
r
2
3
H
11
1
A
2 H
11
1
B
2
500 CHAPTER 8 Multiple Degree-of-Freedom Systems
0 0.5 1 1.5 2
0
1
2
3
4
5
6
Ω
H
11
(Ω)
2
0
2
0.05
2
0.2
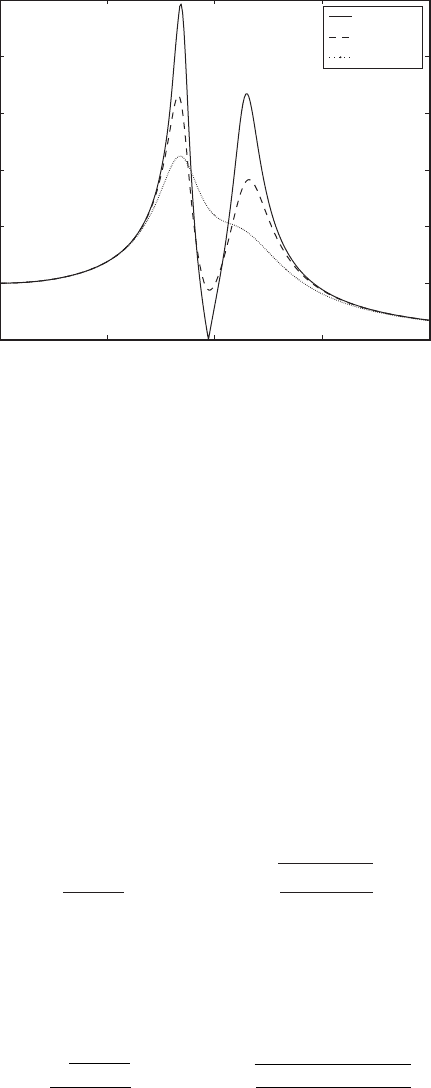
FIGURE 8.20
Amplitude response of primary
mass m
1
with a damped vibration
absorber and when v
r
1:
m
r
0.1, z
1
0.1, and v
r
0.97.
20
J. P. Den Hartog, Mechanical Vibrations, Dover, NY, pp. 87–113 (1985).
21
Equation (8.118), which can be used to determine the optimum values of the absorber parame-
ters, is based on the displacement response of the mass m
1
. If one is interested in determining the
optimum values of the absorber parameters based on the velocity response or acceleration re-
sponse of the mass m
1
, then for the velocity response, the optimal values are
v
r,opt
21 m
r
/2
1 m
r
and
z
2,opt
B
3m
r
11 m
r
5m
2
r
/242
811 m
r
211 m
r
/22
2
The ratio v
r
is optimal or there is optimal tuning when the first of Eqs. (8.118)
is satisfied. The second of Eqs. (8.118) provides the optimal damping value
for the secondary system. It is important to note that the mass ratio is the sole
determining factor for the optimal values. For a general case, when z
1
0, al-
though the optimal condition expressed by Eq. (8.117) is valid, explicit forms
such as Eqs. (8.118) cannot be obtained.
We shall now determine optimal secondary system parameters for a
damped absorber (i.e., z
2
0) so that there is an operating region including
1 wherein the variation of the amplitude of the primary system m
1
as a
function of frequency can remain relatively constant. That is, we would like
to reduce the absorber’s sensitivity to small variations in frequency. This can
be realized through optimization solution techniques.
22
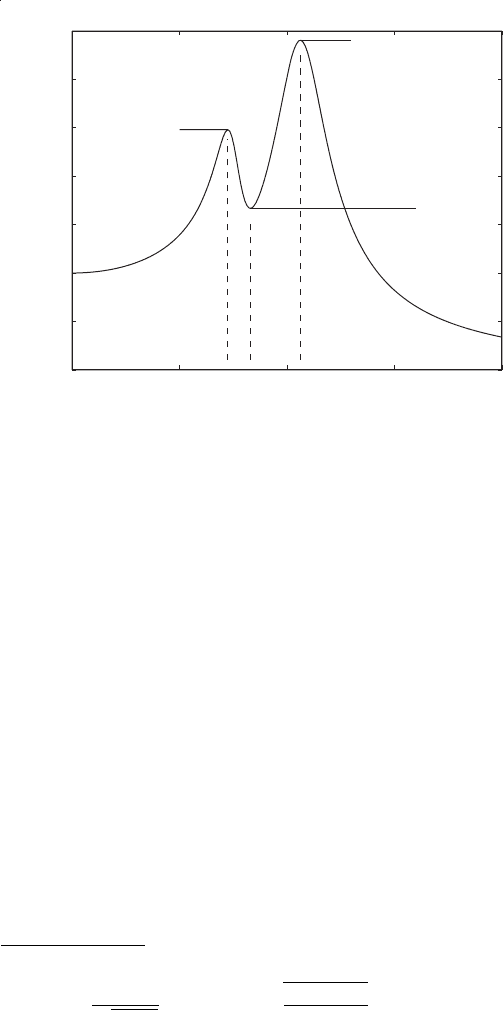
Referring to Figure
8.21, the goal is to find the secondary system parameters for which the peak
amplitudes A and B are equal and are as “small” as possible, while the min-
imum between these peaks C is as close to A and B as possible in terms of
magnitude. In other words, we would like to find the system parameters that
8.6 Vibration Absorbers 501
0 0.5 1 1.5 2
0
0.5
1
1.5
2
2.5
3
3.5
H
11
(Ω
A
)
H
11
(Ω)
H
11
(Ω
B
)
H
11
(Ω
C
)
Ω
Ω
B
Ω
C
Ω
A
FIGURE 8.21
Identification of amplitude response functions to be minimized.
and for the acceleration response, the optimal values are
See G. B. Warburton, op cit., 1982.
22
E. Pennestri, “An Application of Chebyshev’s Min-Max Criterion to the Optimal Design
of a Damped Dynamic Vibration Absorber,” J. Sound Vibration, Vol. 217, No. 4, pp. 757–765,
1998.
v
r,opt
1
21 m
r
and
z
2,opt
B
3m
r
811 m
r
/22
minimize each of the following three maximum values simultaneously:
H
11
(
A
), H
11
(
B
), and 1/H
11
(
C
). This can be stated as follows.
(8.119)
For illustration, we assume that z
1
0.1 and m
r
0.1, 0.2, 0.3 and 0.4
and use readily available numerical procedures
23
to determine the optimum
values of z
2,opt
and v
r,opt
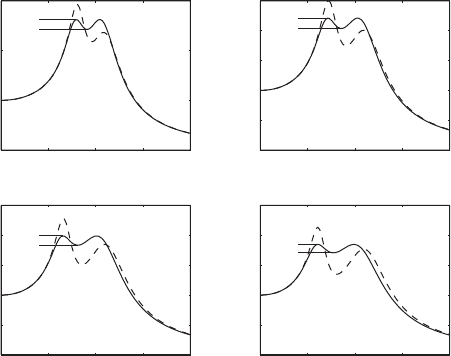
. The results are shown in Figure 8.22 for four differ-
ent values of the mass ratio m
r
. It is seen that these results satisfy the condi-
tion given by Eq. (8.117). Comparing the results shown in the four cases in
Figure 8.22, it is clear that the last case is preferable, since the primary sys-
tem’s response is attenuated to the smallest magnitude over the chosen fre-
quency range. For a given primary system mass, when m
r
0.1, the second-
ary system is the smallest and the displacement amplitude of the secondary
system is likely to be the largest. Since there are restrictions on the amplitude
of motion of the secondary system, if the displacement amplitude of the sec-
ondary system is required to be less than a certain value, then this requirement
z
2
0
subject to: v
r
0
min
v
r
, z
2
51/H
11
1
C
26
min
v
r
, z
2
5H
11
1
B
26
min
v
r
, z
2
5H
11
1
A
26
502 CHAPTER 8 Multiple Degree-of-Freedom Systems
0 0.5 1 1.5 2
0
1
2
3
r,opt
0.862
2,opt
0.199
r,opt
0.711
2,opt
0.309
r,opt
0.655
2,opt
0.343
r,opt
0.778
2,opt
0.265
m
r
0.1
m
r
0.3
m
r
0.2
m
r
0.4
H
11
(Ω)
H
11
(Ω)
H
11
(Ω)
2.62
2.42
0 0.5 1 1.5 2
0
0.5
1
1.5
2
2.5
2.21
2.03
0 0.5 1 1.5 2
0
0.5
1
1.5
2
2.5
H
11
(Ω)
0
0.5
1
1.5
2
2.5
Ω
1.99
1.83
0 0.5 1 1.5 2
Ω
1.85
1.71
FIGURE 8.22
Optimum values for the parameters of a vibration absorber and the resulting amplitude
responses of m
1
for z
1
0.1. The dashed lines are the responses obtained for the optimum
values given by Eqs. (8.118).
23
The MATLAB function fminimax from the Optimization Toolbox was used.

can be included as a constraint for Eqs. (8.119). In terms of design, there are
still other choices one can come up with if Eq. (8.119) is replaced with an-
other set of objectives. However, here, we have pointed out that for a practi-
cal design of an absorber, one will have to resort to numerical means and take
advantage of algorithms such as that used in the present context. Furthermore,
it is noted that when one carries out design, usually there is more than one de-
sign solution to be reckoned with. In addition, the number of degrees of free-
dom is likely to be higher than two in a practical situation.
Upon comparing the results obtained from Eqs. (8.118), we see that there
are differences. For example, when m
r
0.1, Eqs. (8.118) give that v
r,opt
0.909 and z
2,opt
0.168, whereas, from Figure 8.22 we see that the numeri-
cal optimization procedure gives v
r,opt
0.862 and z
2,opt
0.199. Similarly,
for m
r
0.4, Eqs. (8.118) give that v
r,opt
0.714 and z
2,opt
0.234, whereas,
from Figure 8.22 we see that the numerical optimization procedure gives v
r,opt
0.655 and z
2,opt
0.343. However, it is seen from Figure 8.22 that the vari-
ations in the amplitude-response function around the natural frequencies ob-
tained by using the optimum values from Eqs. (8.118) are consistently greater
than those obtained on the basis of Eqs. (8.119).
If the damper c
2
is not connected to mass m
1
and instead connected to a
fixed end, as shown in Figure 8.23, then the governing equations take the form
(8.120)
After using the approach that was employed to obtain Eqs. (8.101), we arrive
at the frequency-response function
(8.121)
It has been found that for this function,
24
the optimum values are
(8.122)
A comparison of the responses for the two types of attachment of the damper
to the absorber mass for m
r
0.1 is given in Figure 8.24. It is seen that the re-
sponses are similar, but with the configuration of the absorber shown in Fig-
ure 8.23, one obtains about a 10% decrease in the maximum magnitude of the
displacement for the same mass ratio.
In designing a vibration absorber, there are other aspects such as the
static deflection of the two degree-of-freedom system, stresses in the absorber
v
r,opt
B
1
1 m
r
and
z
2,opt
B
3m
r
811 m
r
/2 2
`
2
v
2
r
j2z
2
v
r
11
2
21v
2
r
2
2
2
v
2
r
m
r
j2z
2
v
r
11
2
v
2
r
m
r
2
`
H
11
1j2 `
X
1
1j2
F
1
1j2/k
1
`
m
2
x
$
2
c
2
x
#
2
k
2
1x
2
x
1
2 0
m
1
x
$
1
1k
1
k
2
2x
1
k
2
x
2
f
1
1t 2
8.6 Vibration Absorbers 503
24
M. Z. Ren, “A Variant Design of the Dynamic Vibration Absorber,” J. Sound Vibration, 245(4),
pp. 762–770, 2001.
x
1
x
2
c
2
f
(t)
k
2
k
1
m
2
m
1
FIGURE 8.23
A variation of the attachment of the
absorber damper.

springs, displacement of the absorber mass, etc. that one has to deal with.
Many practical hints for designing absorbers are available in the literature.
25
EXAMPLE 8.15 Absorber design for a rotating system with mass unbalance
A rotating system with an unbalanced mass is modeled as a single degree-of-
freedom system with a mass of 10 kg, a natural frequency of 40 Hz, and a
damping factor of 0.2. The system requires an undamped absorber so that the
natural frequencies of the resulting two degree-of-freedom system are outside
the frequency range of 30 Hz to 50 Hz. In addition, the absorber is to be
504 CHAPTER 8 Multiple Degree-of-Freedom Systems
0 0.5
c
2
to m
2
:
opt
0.168
r
0.909
c
2
to fixed end:
opt
0.199
r
1.05
1 1.5 2
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
Ω
H
11
(jΩ)
FIGURE 8.24
Optimized amplitude response of m
1
for two types of damper attachments when m
r
0.1.
25
H. Bachmann et al., Vibration Problems in Structures: Practical Guidelines, Birkhäuser Verlag,
Basel, Germany, Appendix D (1995).
Design Guideline: In many practical situations, a vibration-absorber
system should have a ratio of the absorber mass to the primary system
mass of about one-tenth, a damping factor for the absorber system of
about 0.2 when the primary system is lightly damped, and an uncou-
pled natural frequency of the absorber system that is about 15% less
than that of the primary system.
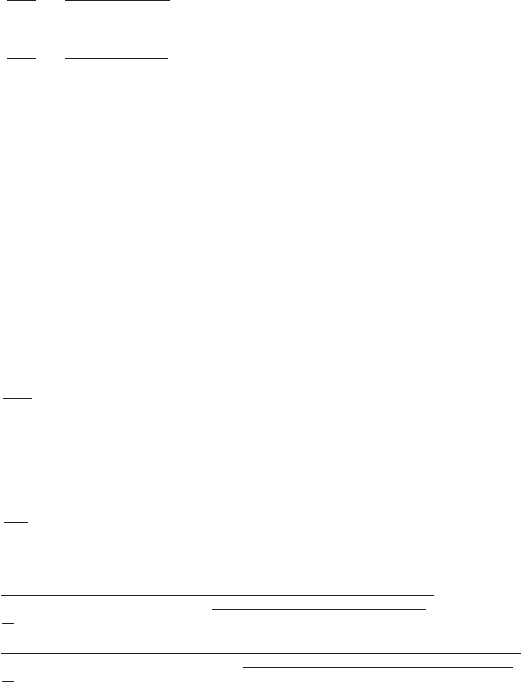
designed such that for force amplitudes of up to 6000 N at 40 Hz, the steady-
state amplitude of the absorber’s response will not exceed 20 mm.
The parameters provided for the primary system are
(a)
For this system, the absorber must be such that the resulting two degree-of-
freedom system’s lowest natural frequency v
1
and the highest natural fre-
quency v
2
have, respectively, the following limits
(b)
or
(c)
where
1
and
2
are the nondimensional natural frequency limits of the ro-
tating system with the absorber. The requirement on the steady-state ampli-
tude of the absorber at 40 Hz is expressed as
(d)
For the absorber to meet the requirements given by Eqs. (b), (c) and (d),
we choose an undamped spring-mass system of stiffness k
2
and mass m
2
. To
meet the requirement given by Eqs. (c), we note from Figure 8.18 that the
larger the mass ratio, the larger the separation between the nondimensional
natural frequencies
1
and
2
. The frequency ratio v
r
is chosen to satisfy
Eq. (8.111); that is,
(e)
Then, Eq. (8.115) is used to determine the nondimensional natural frequen-
cies
1
and
2
for a chosen mass ratio m
r
. Let
(f)
From Eqs. (8.115), (e), and (f), we arrive at
(g) 0.685, 1.460
B
1
2
31 1
2
11 0.6 2 211 1
2
11 0.6 22
2
4 1
2
4
1,2
B
1
2
31 v
2
r
11 m
r
2 211 v
2
r
11 m
r
22
2
4v
2
r
4
m
r
m
2
m
1
0.6
v
r
v
n2
v
n1
1
0X
2
1jv20
vv
n1
251.33
20 10
3
m
2
v
2
v
n1
314.16 rad/s
251.33 rad/s
1.25
1
v
1
v
n1
188.50 rad/s
251.33 rad/s
0.75
v
2
50 2p 314.16 rad/s
v
1
30 2p 188.50 rad/s
z
1
0.2
v
n1
40 2p 251.33 rad/s
m
1
10 kg
8.6 Vibration Absorbers 505

Thus, for the chosen mass ratio m
r
and frequency ratio v
r
, the requirement
given by Eq. (b) is satisfied; that is, the two degree-of-freedom system’s nat-
ural frequencies are outside the range of 30 Hz to 50 Hz.
It remains to be determined if the requirement (d) is satisfied. Making use
of Eqs. (a), (e), and (f), we find that the absorber stiffness k
2
is given by
(h)
Since we have chosen an undamped vibration absorber (i.e., z
2
0) and
v
r
1, we can use Eq. (8.113b) to determine if Eq. (d) is satisfied. Making
use of the given value for the forcing amplitude of 6000 N and the stiffness k
2
calculated in Eq. (h), we find that
(i)
Hence, comparing Eqs. (d) and (h), we find that the second requirement has
also been satisfied. Had we chosen a frequency ratio v
r
different from 1, we
could not have used Eq. (8.113b). Instead, we would have to use Eqs. (8.112)
to determine the steady-state amplitude of the absorber response.
EXAMPLE 8.16
Absorber design for a machine system
A machine has a mass of 200 kg and a natural frequency of 130 rad/s.
An absorber mass of 20 kg and a spring-damper combination is to be at-
tached to this machine so that the machine can be operated in as wide a fre-
quency range as possible around the machine’s natural frequency. We shall
determine the values for the absorber spring constant k
2
and damping coef-
ficient c
2
.
For the given parameters, the mass ratio m
r
is
(a)
The optimal frequency ratio v
r,opt
and the optimal damping ratio z
2,opt
are de-
termined from Eqs. (8.118) as
(b)
The absorber’s natural frequency is
(c)v
n2
v
r,opt
v
n1
0.909 1130 rad/s2 118.17 rad/s
z
2,opt
B
3m
r
811 m
r
2
3
B
3 0.1
811 0.1 2
3
0.168
v
r,opt
1
1 m
r
1
1 0.1
0.909
m
r
m
r
m
1
20 kg
200 kg
0.1
0X
2
0
vv
n1
251.33
`
6000 N
379 10
3
N/m
` 15.83 10
3
m
379 10
3
N/m
10.6 10 kg 2 11 251.33 rad/s 2
2
k
2
m
2
v
2
n2
1m
r
m
1
21v
r
v
n1
2
2
506 CHAPTER 8 Multiple Degree-of-Freedom Systems
Hence, the absorber stiffness is
(d)
and the absorber damping coefficient is
(e)
8.6.2 Centrifugal Pendulum Vibration Absorber
26
Centrifugal pendulum absorbers, which are also known as rotating pendulum
vibration absorbers, are widely used in many rotary applications. For exam-
ple, in rotating shafts, the centrifugal pendulum absorber is often employed
to reduce undesirable vibrations at frequencies that are proportional to the
rotational speed of the shaft. Since the rotational speed can vary over a wide
range, in order to have an effective absorber, the natural frequency of the ab-
sorber should be proportional to the rotational speed. This can be realized by
using the centrifugal pendulum vibration absorber.
A conceptual representation of rotary system with this absorber is illus-
trated in Figure 8.25, where the pendulum absorber moves in the plane con-
taining the unit vectors e
1
and e
2
. These unit vectors are fixed to the pendu-
lum, which has a mass m and length r. The unit vectors and are fixed to
the rotary system. For this two degree-of-freedom system, we will derive the
governing nonlinear equations of the system by using the generalized coordi-
nates u and w, linearize these equations, and use these equations to show how
this absorber can be designed. In Figure 8.25, the angle w is measured relative
to the rotating system, which has a rotary inertia J
O
about the point O, which
is fixed for all time. An external moment M
T
(t) acts on this system.
Equations of Motion
The Lagrange equations given by Eqs. (7.7) are used to get the governing
equations of motion. From Figure 8.25 and Example 1.4, we see that the ve-
locity of the pendulum with respect to the point O is given by
(8.123)V
m
Ru
#
e¿
1
r1w
#
u
#
2e
2
1Ru
#
sin w 2e
1
1Ru
#
cos w r1w
#
u
#
22e
2
e¿
2
e¿
1
794.10 N/1m/s 2
2 0.168 120 kg 2 1118.17 rad/s2
c
2
2z
2
m
2
v
n2
120 kg2 1118.17 rad/s2
2
279.28 10
3
N/m
k
2
m
2
v
2
n2
8.6 Vibration Absorbers 507
26
See, for example: R. G. Mitchiner and R. G. Leonard, “Centrifugal Pendulum Vibration Ab-
sorbers—Theory and Practice,” J. Vibration Acoustics, Vol. 113, pp. 503–507 (1991); M. Sharif-
Bakhtiar and S. W. Shaw, “Effects of Nonlinearities and Damping on the Dynamic Response of
a Centrifugal Pendulum Vibration Absorber,” J. Vibration Acoustics, Vol. 114, pp. 305–311
(1992); and M. Hosek, H. Elmali, and N. Olgac, “A tunable vibration absorber: the centrifugal
delayed resonator,” J. Sound Vibration, Vol. 205, No. (2), pp. 151–165 (1997).
e
2
e
1
e
2
'
e
1
'
r( + )
R
.
.
.
.
.
R cos
R sin
O'
O
R
r
J
o
M
T
(t)
Pivot
m
FIGURE 8.25
Centrifugal pendulum absorber.
Hence, the kinetic energy of the system is
(8.124)
If we ignore the effects of gravity and the stiffness of the rotary system,
27
then there is no contribution to the system potential energy. In addition, since
we have not taken any form of damping into account, there is no dissipation.
For the generalized coordinates we have q
1
u and q
2
w. Then, setting
D V 0 and recognizing that Q
1
M
T
(t) and Q
2
0, the Lagrange
equations given by Eqs. (7.7) reduce to the following:
(8.125)
After substituting Eqs. (8.124) into Eqs. (8.125) and carrying out the indi-
cated differentiations, we obtain the following coupled, nonlinear equations:
(8.126)
Dividing each of the terms in Eqs. (8.126) by mR
2
and introducing the non-
dimensional pendulum length ratio g r/R, we arrive at
(8.127)
where
(8.128)
The rotation u of the rotary system is assumed to consist of two parts, one,
a steady-state rotation vt, due to rotation at a constant angular speed v, and an-
other part c(t) due to a disturbance about this rotation. Thus, we arrive at
(8.129)u1t 2 vt c1t2
J
2
1w 2 g
2
g cos w
J
1
1w 2 J
O
/1mR
2
2 1 g
2
2g cos w
J
2
1w 2u
$
g
2
w
$
g sin wu
#
2
0
J
1
1w 2u
$
J
2
1w 2w
$
g12w
#
u
#
w
#
2
2sin w M
T
1t 2/1mR
2
2
mr 1r R cos w 2u
$
mr
2
w
$
mrRu
#
2
sin w 0
mrRu
#
w
#
sin w mrRw
#
2
sin w M
T
1t 2
3J
O
m1R
2
r
2
2rR cos w24u
$
mr 1r R cos w2w
$
d
dt
a
0T
0w
#
b
0T
0w
0
d
dt
a
0T
0u
#
b
0T
0u
M
T
1t 2
mr 1r R cos w2w
#
u
#
1
2
3J
O
m1R
2
r
2
2rR cos w24u
#
2
1
2
mr
2
w
#
2
1
2
J
O
u
#
2
1
2
m3R
2
u
#
2
r
2
1w
#
u
#
2
2
2rR1u
#
2
w
#
u
#
2cos w4
1
2
J
O
u
#
2
1
2
m31Ru
#
sin w2
2
1Ru
#
cos w r 1w
#
u
#
22
2
4
T
1
2
J
O
u
#
2
1
2
m1V
m
#
V
m
2
508 CHAPTER 8 Multiple Degree-of-Freedom Systems
27
For consideration of rotary system stiffness, see C. Genta, Chapter 5, ibid.

After substituting Eq. (8.129) into Eqs. (8.127), we obtain
(8.130)
Linearized System
We consider “small” oscillations of the pendulum about the position w 0 by
linearizing the trigonometric terms using the approximations sin w w and
cos w 1 and neglecting the quadratic nonlinearities in Eqs. (8.130). After
performing this linearization and making use of Eqs. (8.128), we arrive at the
following linear system of equations:
(8.131)
The natural frequency v
p
of the pendulum is defined as
(8.132)
where we have used the fact that g r/R. Therefore, the pendulum frequency
is linearly proportional to the rotation speed v.
Let us suppose that the external moment applied to the rotating system is
in the form of a harmonic excitation; that is,
(8.133)
Since there is no damping in this case, we use the procedure of Section 8.2.3
and assume a harmonic solution for Eqs. (8.131) of the form
(8.134)
Upon substituting Eqs. (8.134) and (8.133) into Eqs. (8.131) and canceling
the sin v
o
t term, we obtain the following system of equations:
(8.135)
From the second of Eqs. (8.135), it is seen that if the nondimensional pendu-
lum length is chosen so that
(8.136)
then the response amplitude of the rotary system is zero regardless of the
excitation imposed on the system. When g is given by Eq. (8.136), the re-
sponse amplitude of the pendulum is determined from the first of Eqs.
(8.135) as
(8.137)£
M
o
mR
2
v
2
o
g11 g 2
M
o
mR
2
v
2
11 v
2
/v
2
o
2
g
v
2
v
2
o
v
2
o
g11 g 2° 1gv
2
v
2
o
g
2
2£ 0
v
2
o
1J
O
/mR
2
11 g
2
22° v
2
o
g11 g 2£ M
o
/mR
2
w1t 2 £ sin v
o
t
c1t2 ° sin v
o
t
M
T
1t 2 M
o
sin v
o
t
v
p
B
v
2
g
v
2g
v2R/r
11 g2c
$
gw
$
v
2
w 0
3J
O
/mR
2
11 g
2
24c
$
g11 g2w
$
M
T
1t 2/1mR
2
2
J
2
1w 2c
$
g
2
w
$
g sin w1v c
#
2
2
0
J
1
1w 2c
$
J
2
1w 2w
$
g12w
#
c
#
w
#
2
2sin w 2vgw
#
sin w M
T
1t 2/1mR
2
2
8.6 Vibration Absorbers 509
