Balakumar Balachandran, Magrab E.B. Vibrations
Подождите немного. Документ загружается.


To obtain the frequency response function, we set s jv in Eq. (i), which
leads to
(j)
Equation (j) relates the frequency information in the accelerometer measure-
ment to the applied forcing and the system frequency-response functions. If
the excitation moment m(t) 0, then it will be found that the sensor meas-
urement also depends on the frequency-response functions G
12
( jv) and
G
22
( jv).
EXAMPLE 8.12
Frequency-response functions for a structurally damped system
Through this example, we shall illustrate how to obtain the frequency-
response functions of a system with structural damping. As discussed in
Chapter 5, when a vibratory system is excited by a harmonic excitation, the
stiffness elements can be given complex stiffness values to model structural
damping; that is, from Eq. (5.141), we have that
(a)
where k
i
and h
i
, i 1, 2 are constants. The quantities h
1
and h
2
are introduced
to model the structural damping.
We choose Eqs. (8.35) with k
3
0 as the model of a two degree-of-
freedom system subjected to a harmonic excitation and use Eq. (a) to repre-
sent the stiffness quantities. Then Eq. (8.35) becomes
(b)
Introducing the nondimensional quantities given by Eqs. (7.41), Eqs. (b)
can be written as
(c)
Upon solving for X
i
in Eqs. (c), we obtain
(d)
where
(e)
We construct the first set of frequency-response functions by setting
F
2
0. Then Eqs. (d) lead to
D
sd
4
11 jh
1
v
2
r
11 jh
2
211 m
r
22
2
v
2
r
11 jh
1
211 jh
2
2
X
2
1
m
r
k
1
D
sd
3v
2
r
m
r
11 jh
2
2F
1
111 jh
1
2 v
2
r
m
r
11 jh
2
2
2
2F
2
4
X
1
1
k
1
D
sd
31v
2
r
11 jh
2
2
2
2F
1
v
2
r
11 jh
2
2F
2
4
c
11 jh
1
2 v
2
r
m
r
11 jh
2
2
2
v
2
r
m
r
11 jh
2
2
v
2
r
11 jh
2
2 v
2
r
11 jh
2
2
2
de
X
1
X
2
f e
F
1
/k
1
F
2
/1m
r
k
1
2
f
c
k
1
11 jh
1
2 k
2
11 jh
2
2 v
2
m
1
k
2
11 jh
2
2
k
2
11 jh
2
2 k
2
11 jh
2
2 v
2
m
2
de
X
1
X
2
f e
F
1
F
2
f
k
i
씮 k
i
11 jh
i
2
i 1, 2
A
s
1jv2v
2
3G
11
1jv2 L
sensor
G
21
1jv24F1jv 2
490 CHAPTER 8 Multiple Degree-of-Freedom Systems

(f)
The second set of frequency-response functions are obtained by setting F
1
0.
Then Eqs. (d) result in
(g)
Evaluation of Eqs. (f) and (g) for m
r
0.1 and h
1
h
2
0.10 produce graphs
virtually identical to those shown in Figure 8.12.
EXAMPLE 8.13
Amplitude response of a micromechanical filter
There is a class of devices called micromechanical filters that have been used
in signal processing for the last 60 years.
16
These are resonant electro-
mechanical systems that exhibit such characteristics as narrow bandwidth,
low loss, and good stability. These devices are getting considerable attention
again with the advent of small-scale systems being developed in the field
of MEMS.
17
One form of these devices consists of two masses and three
springs as shown in Figure 8.15a. The equivalent vibratory model is shown in
Figure 8.15b. The device shown in Figure 8.15 consists of an inertial element
m
1
being driven by an electrostatic comb transducer. An electrostatic comb
transducer senses the motion of the other inertial element m
2
. Between the
two masses is a coupling spring k
2
. The masses and the geometric parameters
are chosen so that m
1
m
2
, k
1
k
3
, and c
1
c
3
. The goal is to select the ap-
propriate values for m
j
, k
j
, and c
j
to create a filter whose amplitude response
of m
2
is relatively uniform within a specified bandwidth. The degree of uni-
formity is called pass band ripple, and the corresponding magnitudes are usu-
ally expressed in dB.
The filter is described by the transfer function involving the displacement
response of m
2
and the force applied to mass m
1
; that is, we are interested in
H
22
1 2 `
X
2
F
2
/k
1
` `
1
m
r
D
sd
111 jh
1
2 v
2
r
m
r
11 jh
2
2
2
2`
H
12
1 2 `
X
1
F
2
/k
1
` `
v
2
r
11 jh
2
2
D
sd
`
H
21
1 2 `
X
2
F
1
/k
1
` `
v
2
r
11 jh
2
2
D
sd
`
H
11
1 2 `
X
1
F
1
/k
1
` `
1
D
sd
1v
2
r
11 jh
2
2
2
2`
8.5 Transfer Functions and Frequency-Response Functions 491
16
R. A. Johnson, Mechanical Filters in Electronics, John Wiley & Sons, NY (1983).
17
L. Lin et al., “Microelectromechanical Filters for Signal Processing,” J. Microelectromechani-
cal Systems, Vol. 7, No. 3, pp. 286–294 (September 1998); and K. Wang and C. T.-C. Nguyen,
“High-Order Microelectromechanical Electronic Filters,” Proceedings, 10th Annual Interna-
tional Workshop on Micro Electro Mechanical Systems, IEEE Robotics and Automation Society,
pp. 25–30 (January 1997).
the transfer function G
21
(s) X
2
(s)/F
1
(s). We start with Eq. (8.60) and set m
2
m
1
, k
3
k
1
, c
3
c
1
, c
2
0, and f
2
(t) 0 to obtain
(a)
Introducing the quantities
(b)
Eqs. (a) can be rewritten as
(c)
Upon taking the Laplace transforms of the different terms in Eqs.(c) and as-
suming that all the initial conditions are zero, we obtain
(d)
where X
j
(s) is the Laplace transform of x
j
(t), j 1, 2, and F
1
(s) is the Laplace
transform of f
1
(t).
Solving this system of algebraic equations for X
2
(s), we arrive at
k
21
X
1
1s 2 1s
2
2z
1
s 11 k
21
22X
2
1s 2 0
1s
2
2z
1
s 11 k
21
22X
1
1s 2 k
21
X
2
1s 2
F
1
1s 2
k
1
d
2
x
2
dt
2
2z
1
dx
2
dt
11 k
21
2x
2
k
21
x
1
0
d
2
x
1
dt
2
2z
1
dx
1
dt
11 k
21
2x
1
k
21
x
2
f
1
1t 2
k
1
v
n1
B
k
1
m
1
,
2z
1
c
1
m
1
v
n1
,
t v
n1
t,
and
k
21
k
2
k
1
m
1
d
2
x
2
dt
2
c
1
dx
2
dt
1k
2
k
1
2x
2
k
2
x
1
0
m
1
d
2
x
1
dt
2
c
1
dx
1
dt
1k
1
k
2
2x
1
k
2
x
2
f
1
1t 2
492 CHAPTER 8 Multiple Degree-of-Freedom Systems
k
3
c
3
k
2
x
1
, f
1
(t) x
2
k
1
c
1
m
1
m
2
First resonator Second resonator
(b)(a)
Signal
sending port
Signal
sensing port
DC bias
Anchor
Comb shape
transducer
First
resonator
Second
resonator
Coupling
spring
L
1
L
12
L
2
Ground plane
FIGURE 8.15
(a) Layout of a series two resonator micromechanical filter and (b) vibratory model. Source: From A. Lin, et al., "Microelectromechanical
Filters for Signal Processing," Journal of Microelectromechanical Systems, Vol. 7, No. 3, pp. 286 –294 (September 1998). Copyright ©
1998 IEEE. Reprinted with permission.

(e)
where
(f)
The magnitude of the amplitude-response function is obtained by setting s
j in Eqs. (e) and (f ), where v/v
n
. Hence, we obtain
(g)
The damping factors for micromechanical filters vary, but typically they
are low and on the order of 0.001. To give an idea of the amplitude response
of m
2
, we select k
21
0.006 and z
1
0.0015. The numerically obtained re-
sults are shown in Figure 8.16.
In Section 5.3.3, we discussed how a single degree-of-freedom system
could be viewed as a mechanical filter. It was shown that the filter parameters
are dependent on the system resonance and the system’s damping factor. In
this example, we have used a two degree-of-freedom system to construct a
mechanical filter. Examining Figure 8.16, it is seen that the system parameters
have been chosen to place the two system natural frequencies and, hence,
k
21
0
4
4z
1
j
3
212z
2
1
1 k
21
2
2
4z
1
11 k
21
2j1 2k
21
0
1
H
21
1 2 `
X
2
1j2
1F
1
1j2/k
1
2
`
s
4
4z
1
s
3
212z
2
1
1 k
21
2s
2
4z
1
11 k
21
2s 1 2k
21
D
5
1s 2 1s
2
2z
1
s 11 k
21
22
2
k
2
21
X
2
1s 2
1F
1
1s 2/k
1
2
k
21
D
5
1s 2
8.5 Transfer Functions and Frequency-Response Functions 493
FIGURE 8.16
Amplitude response for a micromechanical filter for k
21
0.006 and z
1
0.0015. The data
have been normalized with respect to the maximum value of H
21
().
0.97 0.98 0.99 1 1.01 1.02 1.03
45
40
35
30
25
20
15
10
5
0
Ripple 1.94 dB
Ω
H
21
(Ω) (dB)
3 dB
Ω
cl
0.999
Ω
cu
1.0069

their resonance locations, with a certain frequency separation. This separation
determines the center frequency of the filter and the bandwidth BW of the fil-
ter. Recalling the definitions introduced in Section 5.3.3 for a filter, the band-
width BW is determined by the 3 dB values of the amplitude response,
which occur at
cl
and
cu
, the nondimensional lower and upper cutoff fre-
quencies, respectively. In Section 5.3.3, we discussed that the lower the
damping factor z, the higher the Q factor associated with a filter. Due to the
low damping levels associated with microelectromechanical systems, they
are attractive candidates for mechanical filters. However, unlike in Section
5.3.3 where certain explicit relationships between the filter parameters and
the system parameters of a single degree-of-freedom system could be ob-
tained, when a multiple degree-of-freedom system is designed to act as a fil-
ter, one has to resort to numerical means to determine how a change in a cer-
tain system parameter affects the filter design.
EXAMPLE 8.14
Bell and clapper (continued)
We consider the forced oscillations of the bell and clamper system discussed
in Example 7.8 and shown in Figure 7.10. The governing equations of motion,
which are given by Eq. (h) of this example, are given by
(a)
We shall show that under certain conditions there exists a frequency at which
there is no relative angular motion between the bell and clapper and the bell
will not ring.
We assume a harmonic excitation and let
(b)
The corresponding steady-state response can be assumed as
(c)
Then, upon substituting Eqs. (b) and (c) into Eqs. (a), we obtain the follow-
ing system of equations in matrix form
which can be written more compactly as
(d)
where
c
a
11
1jv2 a
12
1jv2
a
21
1jv2 a
22
1jv2
de
®
1
®
2
f e
M
o
0
f
g c
m
1
d
1
m
2
a 0
0 m
2
d
2
dde
®
1
®
2
f e
M
o
0
f
cv
2
c
m
1
d
2
1
J
1
m
2
a
2
m
2
ad
2
m
2
ad
2
m
2
d
2
2
J
2
d jv c
c
t1
c
t2
c
t2
c
t2
c
t2
d
u
i
1t 2 ®
j
e
jvt
j 1, 2
M
1
1t 2 M
o
e
jvt
m
2
ad
2
u
$
1
1m
2
d
2
2
J
2
2u
$
2
c
t2
u
#
1
c
t2
u
#
2
m
2
gd
2
u
2
0
1m
1
d
2
1
J
1
m
2
a
2
2u
$
1
m
2
ad
2
u
$
2
1c
t1
c
t2
2u
#
1
c
t2
u
#
2
1m
1
d
1
m
2
a2gu
1
M
1
1t 2
494 CHAPTER 8 Multiple Degree-of-Freedom Systems

(e)
Solving for
j
, we obtain
(f)
where
(g)
The complex amplitude of the relative angular displacement between the
bell and clapper is given by
(h)
We see that
1
2
0 when
(i)
Hence, for this frequency there will be no relative motion between the bell
and the clapper, and the bell will not ring.
8.6 VIBRATION ABSORBERS
Vibration absorbers are used in many applications, which include power trans-
mission lines, automobiles, aircraft, optical platforms, and rotating machinery.
In Section 8.2.3, we introduced the undamped vibration absorber and showed
how the absorber system could be designed based on the zeros of the forced
response or the frequency-response function. In this section, we revisit this
problem and broaden the discussion to include damping and different types of
dampers. In Sections 8.6.1 and 8.6.2, we discuss the design of two very dif-
ferent types of vibration absorbers that are based on linear-system principles.
In Sections 8.6.3 to 8.6.5, we introduce nonlinear vibration absorbers and give
an indication of the types of absorber designs that are possible.
18
v
B
m
2
gd
2
m
2
d
2
2
J
2
m
2
ad
2
1v
2
1m
2
d
2
2
J
2
m
2
ad
2
2 m
2
gd
2
2
M
o
¢
®
1
®
2
1a
22
1jv2 a
21
1jv22
M
o
¢
¢ a
11
1jv2a
22
1jv2 a
2
12
1jv2
®
2
a
21
1jv2
M
o
¢
®
1
a
22
1jv2
M
o
¢
a
22
1jv2v
2
1m
2
d
2
2
J
2
2 jc
t2
v m
2
gd
2
a
12
1jv2 a
21
1jv2 m
2
ad
2
v
2
jc
t2
v
a
11
1jv2v
2
1m
1
d
2
1
J
1
m
2
a
2
2 jv1c
t1
c
t2
2 g1m
1
d
1
m
2
a2
8.6 Vibration Absorbers 495
18
The models presented in this section also have been used to estimate the effects of sloshing
dampers (tanks with a fluid in them). See for example: K. Fujii, et al., “Wind-Induced Vibration
of Tower and Practical Applications of Tended Sloshing Damper, J. Wind Engineering Industrial
Aerodynamics, Vol. 33, pp. 263–272, 1990; G. So and S. E. Semercigil, “A Note on a Natural
Sloshing Absorber for Vibration Control,” J. Sound Vibration, Vol. 269, pp. 1119–1127, 2004.

8.6.1 Linear Vibration Absorber
As an illustration of a linear vibration absorber, we consider the system shown
in Figure 8.17. In this system, it is assumed that the primary system with
damping has attached to it a secondary system, the vibration absorber. A dis-
turbance f
1
(t) acts on the primary system and it is assumed that there is no
force acting on the absorber mass m
2
. The governing equations are deter-
mined from Eqs. (8.62) by setting f
2
(t) 0, k
32
0 (k
3
0), and c
32
0
(c
3
0). This leads to
(8.107)
where the different parameters in Eqs. (8.107) are given by Eqs. (7.41).
The design question that is posed is the following: How can a combina-
tion of parameters k
2
, c
2
, and m
2
of the secondary system be chosen so that the
response amplitude of the primary system is at a minimum (or zero) in the
specified frequency range of the excitation? To answer this question, we start
from the responses given by Eqs. (8.101) and obtain.
(8.108)
where D
2
( j) and E
2
( j) are given by Eqs. (8.102). The relation for E
2
( j)
is repeated here for convenience as
(8.109)
In Example 8.3, we considered an undamped primary system and an
undamped vibration absorber, and it was shown that when this primary sys-
tem is subjected to a harmonic excitation at the natural frequency of the
primary system, the vibration absorber can be designed to provide an equal
and opposite force to the excitation force on the primary system. Therefore,
the effective excitation experienced by the primary system is cancelled at
this excitation frequency. In the present case, the primary and secondary sys-
tems are damped. The question is whether the same canceling effect can be
accomplished.
E
2
1j2
2
j12z
2
v
r
2 v
2
r
X
1
1j2
F
1
1j2
G
11
1j2
E
2
1j2
k
1
D
2
1j2
d
2
x
2
dt
2
2z
2
v
r
dx
2
dt
v
r
2
x
2
2z
2
v
r
dx
1
dt
v
2
r
x
1
0
2z
2
m
r
v
r
dx
2
dt
m
r
v
r
2
x
2
f
1
1t 2
k
1
d
2
x
1
dt
2
12z
1
2z
2
m
r
v
r
2
dx
1
dt
11 m
r
v
2
r
2x
1
496 CHAPTER 8 Multiple Degree-of-Freedom Systems
k
2
c
2
x
1
, f
1
(t) x
2
k
1
c
1
m
1
m
2
FIGURE 8.17
System with vibration absorber.

Special Case of Absorber System: z
2
0
From Eqs. (8.108), we see that when E
2
( j) 0 the response of the primary
system given by X
1
( j) is also zero. When z
2
is zero, it is seen from
Eq. (8.109) that E
2
( j) 0 if
v
r
(8.110a)
or equivalently from Eqs. (7.41) that
v v
n2
(8.110b)
Equation (8.110a) is the same as that previously determined from Eq. (h) of
Example 8.3. Thus, if we choose k
2
and m
2
so that Eq. (8.110b) is satisfied,
then we can have a zero of the forced response of the primary system at the
chosen excitation frequency. The implication of this observation is as follows.
Suppose that a harmonic excitation is imposed on the primary mass m
1
at a
frequency v v
n1
, where v
n1
is the natural frequency of the undamped pri-
mary system; that is, the system of Figure 8.17 without the secondary system.
In the absence of the secondary system, since we are exciting the primary sys-
tem at its undamped natural frequency, we expect the response of this linear
system to be “large.” With the inclusion of an undamped secondary system,
and for the choice of k
2
and m
2
satisfying Eqs. (8.110), we find that the re-
sponse of the primary system is zero at v v
n1
. The absorber parameters k
2
and m
2
need to be chosen so that
v
n2
v v
n1
(8.111)
where v
n2
is the natural frequency of the undamped, uncoupled secondary
system. As discussed in Example 8.4, another equation or condition apart
from Eq. (8.111) will be needed to determine the absorber parameters.
In Example 8.3, we found that the response of the primary mass is zero
despite having an excitation acting directly on it, since the force produced by
the absorber on the primary mass is equal and opposite to it. To see if this
holds true for this case, we consider Eqs. (8.63) to (8.65), set k
3
c
2
c
3
f
2
(t) 0, assume that the initial conditions are zero, and set s j to obtain
(8.112)
In Eqs. (8.112), X
1
( j) and X
2
( j) are the complex amplitudes of the
frequency responses of the inertia elements m
1
and m
2
, respectively. From the
second of Eqs. (8.112), if the vibration absorber is chosen to satisfy
Eq. (8.110a), then
(8.113a)
and, hence, it follows from the first of Eqs. (8.112) and Eqs. (7.41) that
(8.113b)X
2
1j2
F
1
1j2
K
1
m
r
v
2
r
F
1
1j2
k
2
X
1
1j2 0
v
2
r
X
1
1j2 1
2
v
2
r
2X
2
1j2 0
1
2
1 m
r
v
2
r
2jz
1
2X
1
1j2 m
r
v
2
r
X
2
1j2
F
1
1j2
K
1
8.6 Vibration Absorbers 497
which is identical to Eq. ( j) of Example 8.3. Thus, the force generated by the
spring k
2
on the primary mass m
1
opposes the disturbing force and is equal to
it in magnitude. As a result, the mass m
1
does not move and instead all of the
energy provided to the system through the forcing f
1
(t) is absorbed by the sec-
ondary system.
Although we would like to take advantage of the zero of the forced re-
sponse at a selected excitation frequency, it is not possible to realize this in
practice. This can occur because of poor frequency tuning of the absorber af-
ter installation or frequency detuning over time caused by changes to the pri-
mary system stiffness and inertia characteristics or by changes to the absorber
system stiffness and inertia characteristics. The possible variations in the
system parameters poses the question: How can one design an absorber to be
effective over a broad frequency range? Before answering this question, we
return to the free oscillation problem. With the introduction of the secondary
system, the absorber, the two degree-of-freedom system has two natural
frequencies. The two natural frequencies of the undamped two degree-of-
freedom system are given by the roots of the characteristic equation, which is
(8.114)
The solution of Eq. (8.114), which is a quadratic equation in
2
,is
(8.115)
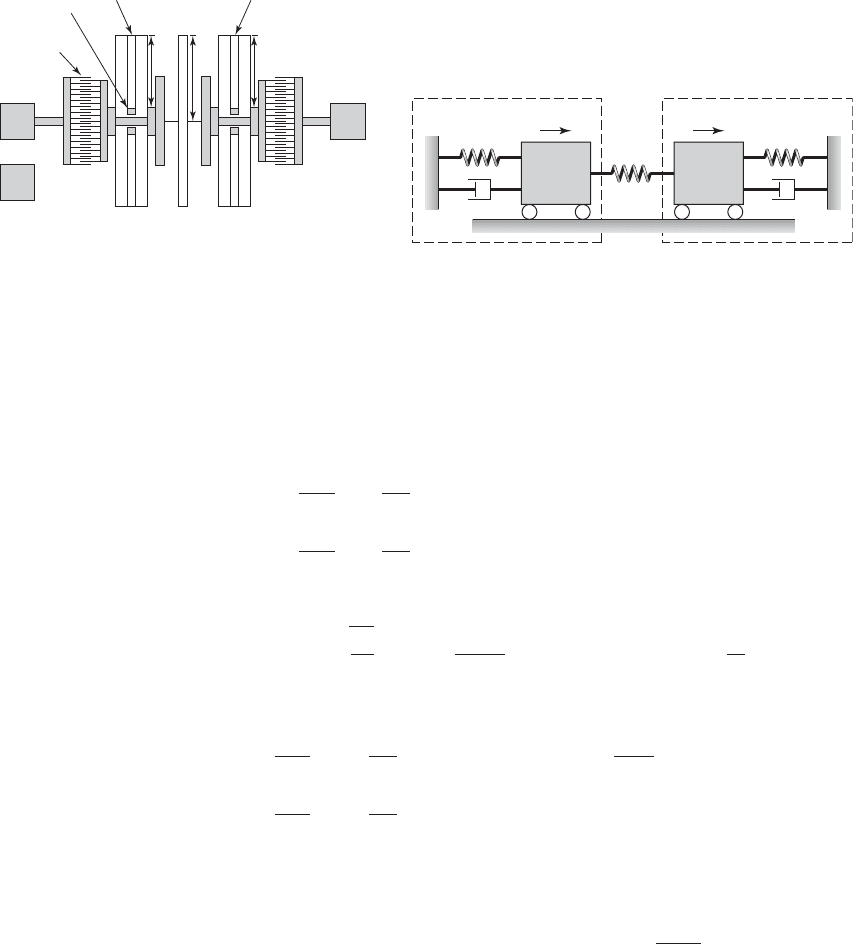
The variations of the two nondimensional natural frequencies
1
and
2
are plotted in Figure 8.18 with respect to the mass ratio m
r
m
2
/m
1
and the
frequency ratio v
r
. As the mass ratio is increased, the separation between the
1,2
B
1
2
c1 v
2
r
11 m
r
2 21 v
2
r
11 m
r
22
2
4v
2
r
d
D
2
1j2
4
31 m
r
v
2
r
v
2
r
4
2
v
2
r
0
498 CHAPTER 8 Multiple Degree-of-Freedom Systems
0 0.5 1 1.5
0.5
1
1.5
2
m
r
Ω
1,2
Ω
1
Ω
2
r
0.9
r
1
r
1.1
FIGURE 8.18
Natural frequencies of a two
degree-of-freedom system with
a vibration absorber as a function
of the mass ratio m
r
.
two natural frequencies increases. In the presence of a harmonic disturbance
acting on the mass of the primary system, we would like the response of mass
m
1
not to be large when we are operating at frequencies close to either of the
two resonance frequencies of the undamped two degree-of-freedom system.
To address this, we return to the forced oscillation problem.
General Case of Absorber System
19
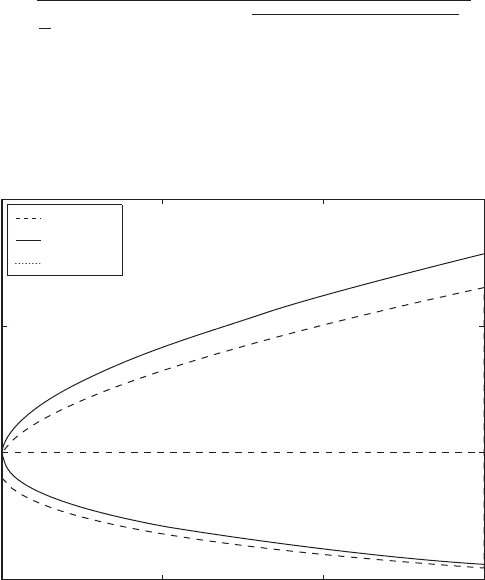
In Figures 8.19 and 8.20, the nondimensional amplitude response
(8.116)
determined from Eq. (8.108) is plotted as a function of the nondimensional
excitation frequency ratio . The mass ratio m
r
, the ratio frequency v
r
, and
the damping of the primary system expressed by z
1
are held fixed in each case,
and the damping factor z
2
is varied. The ratio v
r
is decreased from 1 to 0.97
(i.e., by 3%) in going from Figure 8.19 to Figure 8.20. In both figures, we
have one scenario with an undamped vibration absorber and two scenarios
with two different damped vibration absorbers. The responses seen in Figures
8.19 and 8.20 are characteristic of two degree-of-freedom systems excited by
a harmonic excitation, where the excitation frequency range includes the two
H
11
1 2 0k
1
G
11
1j20
8.6 Vibration Absorbers 499
0 0.5 1 1.5 2
0
1
2
3
4
5
6
2
0.2
Ω
H
11
(Ω)
2
0.05
2
0
FIGURE 8.19
Amplitude response of primary mass
m
1
with a damped vibration
absorber: m
r
0.1, z
1
0.1,
and v
r
1.
19
The response of an absorber system that is limited by an elastic or rigid stop can be found in
the work of A. M. Veprik and V. I. Babitsky, “Non-Linear Correction of Vibration Protection Sys-
tem Containing Tuned Dynamic Absorber,” J. Sound Vibration, Vol. 239 No. 2, pp. 335–356,
2001. The attachment of a spring-mass-damper system to beams, plates, and shells is treated in
the following series of articles: E. O. Ayorinde and G. B. Warburton, “Optimum Absorber Para-
meters for Simple Systems,” Earthquake Engineering and Structural Dynamics, Vol. 8,
pp. 196–217, 1980; E. O. Ayorinde and G. B. Warburton, “Minimizing Structural Vibrations
with Absorbers,” Earthquake Engineering and Structural Dynamics, Vol. 8, pp. 219–236, 1980;
G. B. Warburton, “Optimum Absorber Parameters for Minimizing Vibration Response,” Earth-
quake Engineering and Structural Dynamics, Vol. 9, pp. 251–262, 1981; and G. B. Warburton,
“Optimum Absorber Parameters for Various Combinations of Response and Excitation Parame-
ters,” Earthquake Engineering and Structural Dynamics, Vol. 10, pp. 381–401, 1982.
