Balakumar Balachandran, Magrab E.B. Vibrations
Подождите немного. Документ загружается.

When the tuning of the pendulum absorber is chosen in accordance with Eq.
(8.136), then the zero response of the rotating system in the presence of an ex-
ternal moment can be explained as follows. The pendulum exerts an inertial
moment equal and opposite to the applied external moment on the rotating
system so that the effective external moment felt by the rotating system has
zero magnitude at the disturbance frequency v
o
.
Comparing Eqs. (8.136) and (8.132), it is clear that the pendulum fre-
quency v
p
is equal to the disturbance frequency v
o
; that is, we have a tuned
pendulum absorber.
EXAMPLE 8.17
Design of a centrifugal pendulum vibration absorber for an
internal combustion engine
28
In a four-stroke-cycle internal combustion engine operating at the speed v,it
is necessary to suppress oscillations at the frequency v
o
, which is three times
the operating speed; that is,
(a)
In this case, based on Eqs. (8.136), one can choose a pendulum of the non-
dimensional length
(b)
which means that the pendulum length r needs to be 1/9 the radius R.
8.6.3 Bar Slider System
In this section and in Sections 8.6.4 and 8.6.5, we provide a brief introduction
to vibration absorbers whose design is based on nonlinear system behavior.
We will be pointing out that the oscillations of nonlinear systems can display
vibration characteristics remarkably different from those exhibited by linear
systems.
29
In particular, it will be illustrated that nonlinear systems can show
aperiodic oscillations, such as chaos, and that their response is sensitive to ini-
tial conditions.
30
Consider the bar-slider system
31
shown in Figure 8.26 where M
r
is a
sliding mass on the bar that has a mass moment of inertia J
O
about the fixed
point O. The bar-slider system is assumed to be in a plane perpendicular to
gravity. The slider is restrained by a linear spring-damper combination and
g
v
2
v
2
o
1
9
v
o
3v
510 CHAPTER 8 Multiple Degree-of-Freedom Systems
28
C. Genta, ibid. This reference also provides details of many possible designs of pendulum
absorbers.
29
A. H. Nayfeh and D. T. Mook, 1979, ibid.
30
A. H. Nayfeh and B. Balachandran, 1995, ibid.
31
A. Khajepour, M. F. Golnaraghi, and K. A. Morris, “Application of Center Manifold Theory to
Regulation of a Flexible Beam.” ASME J. Vibrations Acoustics, Vol. 119, pp. 158–165 (1997).
l
r
1
(t)
Slider of
mass M
r
k
c
k
t
J
O
(t)
O
FIGURE 8.26
Bar-slider model. Source: From
A. Khajepour, M. F. Golnaraghi, and
K. A. Morris, “Applications of Center
Manifold Theory to Regulation of a
Flexible Beam.” ASME Journal of
Vibrations Acoustics, Vol. 119,
pp. 158 –165 (1997). Copyright
© 1997 ASME. Reprinted with
permission.

there is a torsion spring attached to the bar at the point O, which restrains the
motions of the bar. To describe the oscillations of this two degree-of-freedom
system, the generalized coordinates r
1
and u are chosen.
We shall derive the governing nonlinear equations of motion and show
that there are quadratic and cubic coupling nonlinearities in the governing
equations. By generating numerical results, it is shown that the slider mass
can absorb the energy input to this two degree-of-freedom system and this
helps attenuate the angular oscillations of the bar. This attenuation of angular
oscillations of the bar is enhanced in the presence of a two-to-one frequency
relationship between the natural frequencies v
r
and v
u
of the linear system.
This type of frequency relationship involving just the natural frequencies of a
multi-degree-of-freedom system is called an internal resonance; in the par-
ticular case considered here, the internal resonance is a two-to-one internal
resonance.
32
Lagrange’s equations given by Eqs. (7.7) are used to establish the gov-
erning equations in terms of the generalized coordinates r
1
and u. Based on
Figure 8.26, the system kinetic energy, the system potential energy, and the
dissipation function D are constructed as follows:
(8.138)
where the position given by length l corresponds to the unstretched position
of the spring to which the slider is attached. Making use of Eqs. (7.7), and not-
ing that the generalized forces Q
1
0 and Q
2
0, we arrive at
(8.139)
On substituting Eqs. (8.138) into Eqs. (8.139) and performing the indi-
cated operations, the result is the following coupled, nonlinear equations of
motion:
quadratic cubic
nonlinearity nonlinearity
(8.140)
quadratic nonlinearities cubic nonlinearities
3J
O
M
r
l
2
4u
$
k
t
u 2M
r
l1r
#
1
u
#
r
1
u
$
2 2M
r
r
1
1r
#
1
u
#
r
1
u
$
2 0
M
r
r
$
1
cr
#
1
kr
1
M
r
lu
#
2
M
r
r
1
u
#
2
0
d
dt
a
0T
0u
#
b
0T
0u
0D
0u
#
0V
0u
0
d
dt
a
0T
0r
#
1
b
0T
0r
1
0D
0r
#
1
0V
0r
1
0
D
1
2
cr
#
2
1
V
1
2
k
t
u
2
1
2
kr
2
1
T
1
2
J
O
u
#
2
1
2
M
r
r
#
2
1
1
2
M
r
1l r
1
2
2
u
#
2
8.6 Vibration Absorbers 511
32
Vibration absorbers based on internal resonances have been studied since the 1960s; see, for exam-
ple, the following articles: E. Sevin, “On the Parametric Excitation of a Pendulum-type Vibration
Absorber,” ASME J. Applied Mechanics, Vol. 28, pp. 330–334 (1961); and R. S. Haxton and A. D. S.
Barr, “The Autoparametric Vibration Absorber,” ASME J. Eng. Industry., Vol. 94, pp. 119–125 (1972).
⎫
⎬
⎭
⎫
⎬
⎭
⎫
⎪
⎬
⎪
⎭
⎫
⎪
⎬
⎪
⎭

In Eqs. (8.140), the source of the coupling is the quadratic and cubic nonlin-
earities. For small oscillations about the system equilibrium position r
1
0
and u 0, the nonlinear equations are linearized to obtain
(8.141)
From the linearized system of Eqs. (8.141), it is seen that the radial motions
of the slider and the angular oscillations of the bar are uncoupled. Hence, the
undamped system natural frequencies are readily identified as
(8.142)
The ratio of the two natural frequencies given in Eqs. (8.142) is critical for the
design of the nonlinear vibration absorber.
We rewrite the nonlinear equations given by Eqs. (8.140) in terms of the
following nondimensional quantities:
(8.143)
Then Eqs. (8.140) become
(8.144)
where the overdot now indicates the derivative with respect to the nondimen-
sional time t. From these equations, it is seen that the motion of the system
can be studied in terms of the following nondimensional parameters: a) the
frequency ratio v
c
, b) the mass ratio m, and c) the damping ratio z.
For arbitrary magnitudes of oscillations, the nonlinear equations (8.144)
can only be solved numerically.
33
To illustrate the absorber action, we as-
sume that the system is subjected to an initial rotation u(0) 0.3 rad (i.e.,
17.2°), an initial radial displacement r(0) 0, and that the initial radial ve-
locity and the initial angular velocity are zero. For m 0.3, z 0.15, and
v
c
0.5, 1.5, 2, and 2.5, the numerically generated results are presented in
Figure 8.25.
It is seen from Figure 8.27 that when v
c
2.0, the angular oscillations
decay more rapidly than in the other cases considered. In this special case, the
coupling between the radial oscillations of the slider mass and the angular os-
cillations of the bar are enhanced due to the nonlinear coupling terms. These
31 2m11 r 2r 4u
$
u 2m11 r2r
#
u
#
0
r
$
2zv
c
r
#
v
2
c
r 11 r 2u
#
2
0
r1t 2
r
1
1t 2
l
,
m
M
r
J
O
/l
2
M
r
t v
u
t,
v
c
v
r
v
u
,
z
c
2M
r
v
r
,
v
u
B
k
t
J
O
M
r
l
2
v
r
B
k
M
r
3J
O
M
r
l
2
4u
$
k
t
u 0
M
r
r
$
1
cr
#
1
kr
1
0
512 CHAPTER 8 Multiple Degree-of-Freedom Systems
33
The MATLAB function ode45 was used.

types of frequency relationships have been used to construct vibration con-
trollers for free oscillations and forced oscillations.
34
8.6.4 Pendulum Absorber
35
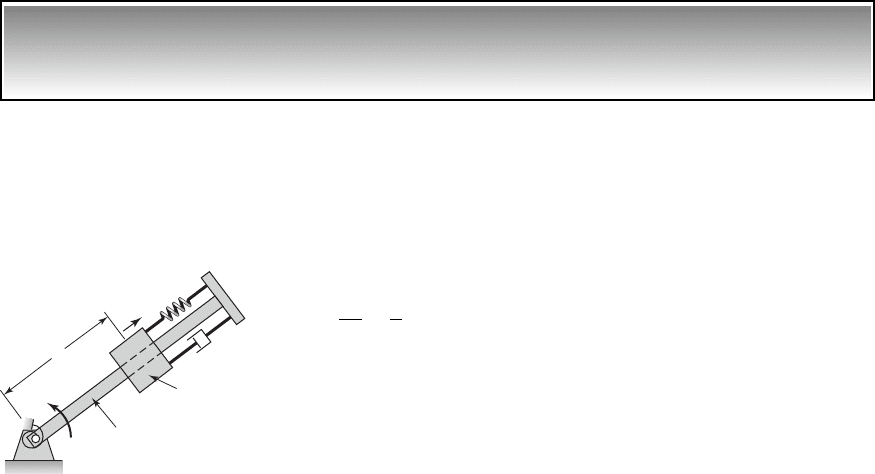
Consider the pendulum absorber system shown in Figure 8.28. This system
consists of a mass M mounted on a combination of a linear spring and a lin-
ear viscous damper. A pendulum of mass m and length l is attached to the
mass M. A linear torsion damper with a damping coefficient c
t
is also in-
cluded. To describe the motions of this two degree-of-freedom system, the
generalized coordinates x and w are used. The coordinate x is measured from
the system static-equilibrium position.
When the system is forced harmonically along the vertical direction, the
up and down motions of the system can be undesirable, especially when the
excitation frequency is close to the system natural frequency associated with
the vertical motions. To attenuate these up and down oscillations, the pendu-
lum is designed as an absorber, so that the input energy along the vertical di-
rection is absorbed as angular oscillations of the pendulum.
The harmonic forcing acting on the mass M is assumed to have an am-
plitude F
o
and a frequency v. Starting from the Lagrange equations given by
8.6 Vibration Absorbers 513
34
A. H. Nayfeh, Nonlinear Interactions, John Wiley & Sons, NY, Chapter 2 (2000).
35
A. Tondl, T. Ruijgork, F. Verhulst, and R. Nabergoj, Autoparametric Resonance in Mechanical
Systems, Cambridge University Press, Cambridge, England, Chapter 4 (2000); Y. Song, et al.,
“The Response of a Dynamic Vibration Absorber System with a Parametrically Excited Pendu-
lum,” J. Sound Vibration, Vol. 259, No. 4, pp. 747–759, 2003.
0 20 40 60 80
0.4
0.2
0
0.2
c
0.5
c
1.5
c
2
c
2.5
0 20 40 60 80
0.2
0
0.2
0 20 40 60 80
0.05
0
0.05
0 20 40 60 80
0.2
0
0.2
0 20 40 60 80
0.05
0
0.05
0 20 40 60 80
0.2
0
0.2
0 20 40 60 80
0.05
0
0.05
r() r() r() r()
0 20 40 60 80
0.2
0
0.2
() () () ()
FIGURE 8.27
Response of the slider-mass system for z 0.15, m 0.3, and v
c
0.5, 1.5, 2.0, and 2.5.

514 CHAPTER 8 Multiple Degree-of-Freedom Systems
Eqs. (7.7) and recognizing that the generalized forces are Q
1
F
o
cos vt and
Q
2
0, we find that the governing equations are obtained from
(8.145)
The system kinetic energy T is given by
(8.146)
where, in arriving at Eq. (8.146), we have made use of the pendulum velocity
(8.147)
The system potential energy V and the dissipation function D take the form
(8.148)
After substituting Eqs. (8.146) and (8.148) in Eqs. (8.145) and carrying out
the indicated operations, the result is the following system of coupled nonlin-
ear equations:
nonlinear terms
(8.149)
nonlinear terms
ml
2
w
$
c
t
w
#
mlx
$
sin w mgl sin w 0
1M m2x
$
cx
#
kx ml 3w
$
sin w w
#
2
cos w4 F
o
cos vt
D
1
2
cx
#
2
1
2
c
t
w
#
2
V
1
2
kx
2
mgl11 cos w 2
V
m
1lw
#
cos w2i 1x
#
lw
#
sin w2j
1
2
Mx
#
2
1
2
m31lw
#
cos w2
2
1x
#
lw
#
sin w2
2
4
T
1
2
Mx
#
2
1
2
m1V
m
#
V
m
2
d
dt
a
0T
0x
#
b
0T
0x
0D
0x
#
0V
0x
0
d
dt
a
0T
0w
#
b
0T
0w
0D
0w
#
0V
0w
F
o
cos vt
l
.
mg
c
t
m
M
x
c
l
k
j
i
F
o
cos t
FIGURE 8.28
System with pendulum absorber.
⎫
⎪
⎪
⎬
⎪
⎪
⎭
⎫
⎪
⎪
⎬
⎪
⎪
⎭

For small oscillations about the system equilibrium position x 0 and
w 0, Eqs. (8.149) are linearized by using the approximations sin w w and
cos w 1 and dropping the nonlinear terms. The result is
(8.150)
From Eqs. (8.150) it is seen that the vertical motions of the system are un-
coupled from the angular oscillations of the pendulum in the linear system.
Therefore, the undamped system natural frequencies is readily identified as
(8.151)
The ratio of the two natural frequencies given in Eqs. (8.151) is critical for the
considered nonlinear vibration absorber design.
We introduce the following nondimensional quantities
(8.152)
into Eqs. (8.149) and arrive at
(8.153)
where the overdot now indicates the derivative with respect to t. It is seen
from the form of Eqs. (8.153) that the motions of this nonlinear system can
be studied in terms of the following nondimensional quantities: a) the mass
ratio m
r
, b) the frequency ratio v
r
, c) the damping ratios z
x
and z
t
, d) the forc-
ing amplitude f
o
, and e) the forcing frequency .
For arbitrary magnitudes of oscillations, the nonlinear system given by
Eqs. (8.153) can only be solved numerically. Furthermore, from the second
of Eqs. (8.153), it is seen that w 0 is always a solution of this system.
Therefore, if nontrivial solutions for w are sought, one has to be careful in
picking an initial condition for which w(0) 0. As pointed out in Section
4.5.2, initial conditions are critical in determining the response of a nonlin-
ear system. Since we would like the absorber to be effective, when the forc-
ing frequency is in resonance with the system natural frequency for vertical
motions, we choose 1. Furthermore, to enhance the nonlinear coupling
between the angular oscillations and the up and down translations, we set
v
r
0.5; that is, the natural frequency of the pendulum oscillations is one
half of the natural frequency of vertical translations of the system. Light
damping is also considered. The numerical results
36
generated are presented
w
$
2z
t
w
#
1v
2
r
z
$
2sin w 0
z
$
2z
x
z
#
z m
r
3w
$
sin w w
#
2
cos w4 f
o
cos t
2z
x
c
1M m2v
x
,
2z
t
c
t
ml
2
v
x
,
m
r
m
1M m2
z
x
l
,
t v
x
t,
v
r
v
w
v
x
,
v
v
x
,
f
o
F
o
1M m2lv
2
x
v
w
B
g
l
v
x
B
k
m M
ml
2
w
$
c
t
w
#
mglw 0
1M m2x
$
cx
#
kx F
o
cos vt
8.6 Vibration Absorbers 515
36
The MATLAB function ode45 was used.
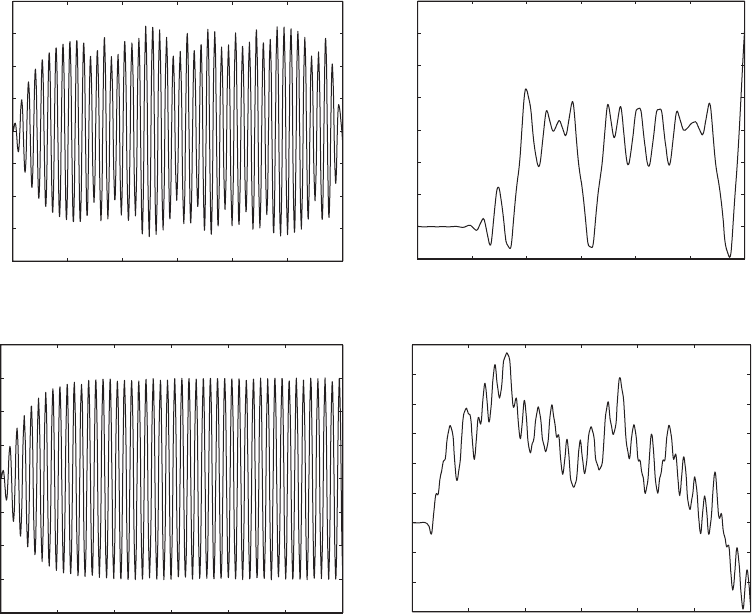
in Figure 8.29 for two different values of non-dimensional forcing mag-
nitude f
o
. The initial condition for the angular state is picked as w(0)
0.02 rad (1.15°) to avoid converging to the trivial solution w 0. The initial
translation state z, the initial angular velocity , and the initial translation
velocity are all zero.
It is seen that although the system is being driven at the resonance
of the system’s translation motions, the pendulum absorber is effective in
limiting them. However, the translation motions and the angular motions
have an aperiodic character, despite a harmonic input into this system.
The pendulum motion is an irregular mixture of oscillations and rotation.
(Recall that one complete revolution of the pendulum is 2p radians.) The
aperiodic motions seen in Figure 8.29 are examples of chaotic motions,
which have some special characteristics. For more details on how these
z
#
w
#
516 CHAPTER 8 Multiple Degree-of-Freedom Systems
0 50 100 150 200 250 300
0.4
0.3
0.2
0.1
0
0.1
0.2
0.3
0.4
t
0 50 100 150 200 250 300
2
0
2
4
6
8
10
12
14
t
w(t)w(t)
(a)
0 50 100 150 200 250 300
4
3
2
1
0
1
2
3
4
t
0 50 100 150 200 250 300
15
10
5
0
5
10
15
20
25
30
t
(b)
z(t)z(t)
FIGURE 8.29
Response of the system with the pendulum absorber for 1, v
r
0.5, z
x
0.05, z
t
0.005, and m
r
0.05: (a) f
o
0.03
and (b) f
o
0.3.
characteristics can be identified, the reader is referred to the nonlinear dy-
namics literature.
37
8.6.5 Particle Impact Damper
A particle damper is a passive device composed of one or more cavities that are
filled with dry granular particles such as granules of aluminum, lead, tungsten
carbide, or ceramic. These cavities either can be an integral part of the vibrat-
ing system or be externally attached to the system. The particles move freely
within the cavity, and they remove vibratory energy from the host system
through losses that occur during their inelastic collisions amongst each other as
well as with the cavity walls. The collisions amongst the particles can occur in
a random manner. By comparison to tuned mass dampers, particle impact
dampers are attractive for the following reasons: (1) they can provide effective
damping over a wide range of frequencies and accelerations, (2) they have a
very simple and inexpensive design, and (3) they can operate in harsh environ-
ments. They have been successfully used in such applications as cutting tools,
turbine blades, and various types of structures and structural elements.
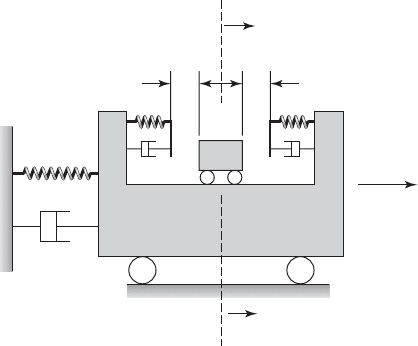
Here, we illustrate a fundamental mechanism by which these dampers
work by considering a single particle damper attached to a single degree-of-
freedom system (the host system to be damped), as shown in Figure 8.30. In-
teractions amongst the particles are not considered in this elementary model.
The host system has a mass m
1
, a damping coefficient c
1
, and a stiffness k
1
.
The particle has a mass m
2
, and it is assumed to slide without friction in a cav-
ity on top of the mass m
1
. The mass m
2
can traverse a maximum distance of
8.6 Vibration Absorbers 517
37
A. H. Nayfeh and B. Balachandran, 1995, ibid; F. C. Moon, Chaotic and Fractal Dynamics: An
Introduction for Applied Scientists and Engineers, John Wiley & Sons, NY (1992).
x
2
x
1
c
1
m
1
F
o
p(t)
k
1
k
2
k
2
c
2
c
2
m
2
dd
FIGURE 8.30
Single particle impact damper.
2d without contacting the walls of the cavity, which each have a stiffness k
2
.
The viscous damper with damping coefficient c
2
has been used to model the
loss associated with the inelastic collision between the particle and the cavity
wall. This type of loss has been discussed in Example 4.4, where the coeffi-
cient of restitution e was introduced. The relationship between e and the
damping factor z is given by Eq. (b) of Example 4.4. The mass m
1
is subjected
to a time-varying disturbance of magnitude F
o
and shape p(t).
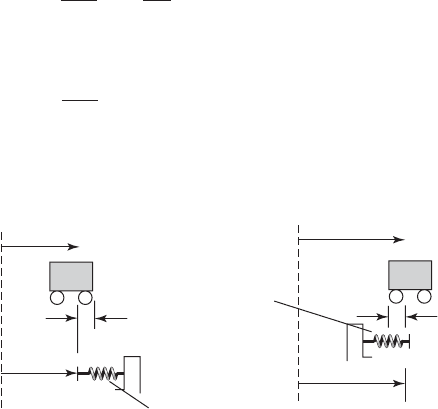
To develop the equations of motion, we consider the scenarios illustrated
in Figure 8.31. When the mass m
2
moves towards the right more than the
mass m
1
moves towards the right, the right spring is compressed when
x
2
(x
1
d) 0. The compressive force generated in the right spring
has the magnitude k
2
(x
1
d x
2
). When the mass m
1
moves towards the
right more than the mass m
2
moves, the left spring is compressed when
(x
1
d) x
2
0. The compressive force generated in the left spring has the
magnitude k
2
(x
1
d x
2
). A similar reasoning is used to determine the force
generated by the viscous dampers. With these considerations, the equation of
motion governing the host system with mass m
1
is
38
(8.154)
The equation of motion governing the particle with mass m
2
is
(8.155)
where p(t) is the time-varying forcing function, F
o
is the forcing magnitude,
and , j (1, 2), and x
#
j
dx
j
/dt
m
2
d
2
x
2
dt
2
k
2
h1x
1
, x
2
2 c
2
g1x
#
1
, x
#
2
2 0
m
1
d
2
x
1
dt
2
c
1
dx
1
dt
k
1
x
1
k
2
h1x
1
, x
2
2 c
2
g1x
#
1
, x
#
2
2 F
o
p1t 2
518 CHAPTER 8 Multiple Degree-of-Freedom Systems
38
See S. Chatterjee, A. K. Mallik, and A. Ghosh, “On Impact Dampers for Non-Linear Vibrating
Systems,” Journal Sound Vibration, 187 (1995) pp. 403–420 and S. F. Masri and T. K. Caughey,
“On the Stability of the Impact Absorber,” Journal of Applied Mechanics, E33 (1966)
pp. 586–592.
m
2
x
2
k
2
x
1
d
Right
spring
(a) (b)
m
2
x
2
k
2
x
1
d
Left
spring
FIGURE 8.31
Relative motion of the masses: (a) m
2
moves towards the right more than m
1
so that contact
is made with the right spring and (b) m
1
moves towards the right more than m
2
and contact is
made with the left spring. The spring is compressed by an amount .

(8.156)
We have used the unit step function u(x) in the functions h(x
1
, x
2
) and g(x
1
, x
2
)
to express the contact forces due to the k
2
c
2
combination on either the left
side or the right side.
Equations (8.154) and (8.155) are nonlinear, since the contact forces are
piecewise functions. These forces vanish when the mass m
2
does not make
contact with mass m
1
and they are non-zero otherwise. The host system,
which is linear, becomes nonlinear after inclusion of the particle damper.
In order to simplify these equations, we introduce the following nondi-
mensional parameters
Then, Eqs. (8.154) to (8.156) become, respectively,
(8.157)
where
(8.158)
and , j 1, 2.
We now examine several different scenarios by using Eqs. (8.157) and
(8.158). In all cases, we assume that the initial conditions are zero; that is,
y
1
(0) 0, , y
2
(0) 0, and .
Pulse Response with and without Particle Damper: Time-Domain Results
We first obtain the system’s response to a rectangular pulse of duration t
0.025; that is, to a forcing p(t) [u(t) u(t 0.025)]. The numerically ob-
tained results
39
are shown in Figure 8.32. It is seen that with a suitable com-
bination of parameters, the particle damper can dramatically decrease the sys-
tem’s settling time. This is equivalent to increasing the damping coefficient c
1
.
From the velocity response of the particle shown in Figure 8.32c, we see that
the velocity response has features similar to those shown for the impact re-
sponse of a car bumper in Figure 4.6; that is, when the particle is no longer in
contact with the spring, it travels with a constant speed until the next contact
is made.
y
#
2
10 2 0y
#
1
10 2 0
y
#
j
dy
j
/dt
g1y
#
1
, y
#
2
2 1y
#
1
y
#
2
2u1y
1
y
2
12 1y
#
1
y
#
2
2u1y
1
y
2
12
h1y
1
, y
2
2 1y
1
y
2
12u1y
1
y
2
12 1y
1
y
2
12u1y
1
y
2
12
d
2
y
2
dt
2
k
21
m
21
h1y
1
, y
2
2 2z
c
21
m
21
g1y
#
1
, y
#
2
2 0
d
2
y
1
dt
2
2z
dy
1
dt
y
1
k
21
h1y
1
, y
2
2 2zc
21
g1y
#
1
, y
#
2
2 f
o
p1t 2
v
v
n
,
k
21
k
2
k
1
,
m
21
m
2
m
1
,
c
21
c
2
c
1
,
2z
c
1
m
1
v
n
y
j
x
j
d
j 1, 2
v
n
B
k
1
m
1
,
t v
n
t,
f
o
F
o
dk
1
g1x
#
1
, x
#
2
2 1x
#
1
x
#
2
2u 1x
1
x
2
d2 1x
#
1
x
#
2
2u 1x
1
x
2
d2
h1x
1
, x
2
2 1x
1
x
2
d2u1x
1
x
2
d2 1x
1
x
2
d2u1x
1
x
2
d2
8.6 Vibration Absorbers 519
39
The MATLAB function ode45 was used.
